A process-level hierarchical structural decomposition analysis (SDA) of energy consumption in an integrated steel plant
来源期刊:中南大学学报(英文版)2017年第2期
论文作者:廖胜明 刘骁浚 饶政华 刘刚
文章页码:402 - 412
Key words:structural decomposition analysis; input-output table; energy consumption; embodied energy; integrated steel plant
Abstract: A hierarchical structural decomposition analysis (SDA) model has been developed based on process-level input-output (I-O) tables to analyze the drivers of energy consumption changes in an integrated steel plant during 2011-2013. By combining the principle of hierarchical decomposition into D&L method, a hierarchical decomposition model for multilevel SDA is obtained. The developed hierarchical IO-SDA model would provide consistent results and need less computation effort compared with the traditional SDA model. The decomposition results of the steel plant suggest that the technology improvement and reduced steel final demand are two major reasons for declined total energy consumption. The technical improvements of blast furnaces, basic oxygen furnaces, the power plant and the by-products utilization level have contributed mostly in reducing energy consumption. A major retrofit of ancillary process units and solving fuel substitution problem in the sinter plant and blast furnace are important for further energy saving. Besides the empirical results, this work also discussed that why and how hierarchical SDA can be applied in a process-level decomposition analysis of aggregated indicators.
Cite this article as: LIU Xiao-jun, LIAO Sheng-ming, RAO Zheng-hua, LIU Gang. A process-level hierarchical structural decomposition analysis (SDA) of energy consumption in an integrated steel plant [J]. Journal of Central South University, 2017, 24(2): 402. DOI: 10.1007/s11171-017-3442-3.
J. Cent. South Univ. (2017) 24: 402-412
DOI: 10.1007/s11171-017-3442-3
LIU Xiao-jun(刘骁浚), LIAO Sheng-ming(廖胜明), RAO Zheng-hua(饶政华), LIU Gang(刘刚)
School of Energy Science and Engineering, Central South University, Changsha 410083, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: A hierarchical structural decomposition analysis (SDA) model has been developed based on process-level input-output (I-O) tables to analyze the drivers of energy consumption changes in an integrated steel plant during 2011-2013. By combining the principle of hierarchical decomposition into D&L method, a hierarchical decomposition model for multilevel SDA is obtained. The developed hierarchical IO-SDA model would provide consistent results and need less computation effort compared with the traditional SDA model. The decomposition results of the steel plant suggest that the technology improvement and reduced steel final demand are two major reasons for declined total energy consumption. The technical improvements of blast furnaces, basic oxygen furnaces, the power plant and the by-products utilization level have contributed mostly in reducing energy consumption. A major retrofit of ancillary process units and solving fuel substitution problem in the sinter plant and blast furnace are important for further energy saving. Besides the empirical results, this work also discussed that why and how hierarchical SDA can be applied in a process-level decomposition analysis of aggregated indicators.
Key words: structural decomposition analysis; input-output table; energy consumption; embodied energy; integrated steel plant
1 Introduction
The iron and steel industry is a resource and energy intensive industry. Especially, the integrated steel making process is the dominant steel production route, which has produced 73.7% of total world crude steel in 2014. In order to maintain competitiveness and reduce energy consumption as well as environmental impact, the owners of the integrated steel plants are increasingly motivated in energy management. A crucial technique in energy management is to conduct an ex-post analysis on past energy consumption trends based on historic data of production and consumption. How energy consumption of integrated steel plants has changed over time? What are the major drivers of past and present energy consumption trends? Which process units are the main contributors to reduce or increase the energy use? What technology improvements or inefficiencies play a dominant role in reducing or increasing the energy consumption? To better answer the above questions, the decomposition analysis is applied.
The decomposition analysis is an effective tool that identifies and quantifies the driving forces behind the changes of an aggregation indicator over time. The two main approaches of decomposition analysis are index decomposition analysis (IDA) and structural decomposition analysis (SDA) based on input-output (I-O) models. The relationships and the differences between them were discussed [1]. With respect to theoretical foundation, logarithmic mean divisia index (LMDI) is the most popular method in IDA while D&L [1] is the most widely used method in SDA. In terms of decomposition level of the aggregated indicators, previous decomposition studies are mainly divided into three categories: national level, sector/industry level, and regional (province, city, etc.) level. National level decomposition analysis means that the decomposed aggregate indicators are country-level indicators and all related major sectors are considered. The recent studies are IDA of CO2 emissions changes in USA [2], Philippines [3], Spain [4], 33 world countries [5], IDA of energy intensities and use in Latvia [6], European countries [7], SDA of residential indirect CO2 emissions in China [8], and SDA of energy footprint for 186 countries [9]. Sector/industry level decomposition analysis means that the decomposed aggregate indicators only represent one particular sector or industry of a country. Recent empirical studies were IDA of CO2 emissions changes from China’s mining sector [10], road transport sector [11], aluminum industry [12], power sector in the European countries [13], and SDA of changes in road freight transport for European countries [14]. Regional level decomposition analysis means that
the decomposed aggregate indicators are province-level or city-level indicators. The recent studies can be found in IDA of CO2 emissions changes in Chongqing [15] and Jiangsu Province, China [16], IDA of household daily travel CO2 emissions [17], SDA of CO2 emissions changes [18] and SDA of water use in Beijing, China [19].
The decomposition analysis has been widely applied in national, sector/industry and regional scale. However, a process-level decomposition analysis is still lacking. This work attempts to fill this gap in the literature by presenting an IO-SDA of energy use for an integrated steel plant located in Hunan province, China. The SDA is preferred because the data are sufficient to construct I-O tables for SDA, which can provide more detailed decomposition of technology and demand changes compared with IDA. Moreover, inspired by multilevel IDA and Matiroshka principle, a hierarchical decomposition model using D&L method has been developed and applied in this work.
2 Methodology
2.1 Process level input-output model
By extending the previous enterprise input-output (I-O) models proposed by LIN et al [20] and ALBINO et al [21], the process-level physical I-O model has been developed for calculating energy consumption indicators, namely the embodied energy of main products and the total energy consumption of production processes (i.e. the integrated steel plant in this wrok).
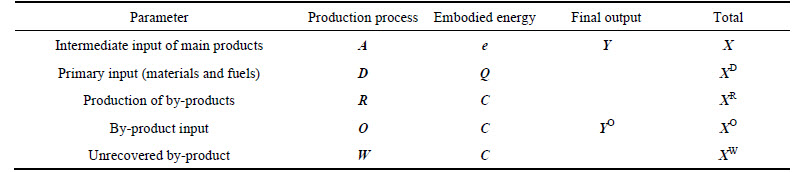
It is assumed that there is only one main product or a homogenous group of main products per process. Let us consider the production system which contains n categories of processes. Each process is classified based on its main product. There are s types of primary inputs (raw materials and fuel) imported to the site. Besides main products, v categories of by-products or “waste for recycling” are generated, recycled (for internal or external usage), and discarded. The conceptual input- output table of the production system is expressed in Table 1, where A=[Aij] is a matrix of direct coefficients for intermediate main product inputs; D=[Dkj] is a matrixof direct coefficients for primary inputs (materials and fuel); R=[Rfj] is a matrix of direct coefficients for by-products production; O=[Ogj] is a matrix of direct coefficients for by-products intermediate (on-site) consumption; W=[Whj] is a direct coefficient matrix of by-products losses. The above direct input-output coefficients are technical coefficients reflecting the technical status of production processes studied. X=[Xi] is a total output vector of main products; Y=[Yi] is a final output (deliveries leaving the site to customers and storage) vector of main products. It is also known as thefinal demand vector. 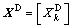 is a vector of total primary inputs;
is a vector of total primary inputs;  is a vector of total by-products production;
is a vector of total by-products production; 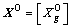 is a vector of total by-products utilization;
is a vector of total by-products utilization; 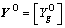 is a final output vector of by-products;
is a final output vector of by-products; 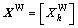 is a vector of total by-products losses; e=[ei] is a vector of embodied energy for main products; O=[Ok] is a vector of embodied energy for primary inputs; C=[Cg] is a vector of credit embodied energy for by-products.
is a vector of total by-products losses; e=[ei] is a vector of embodied energy for main products; O=[Ok] is a vector of embodied energy for primary inputs; C=[Cg] is a vector of credit embodied energy for by-products.
The basic relationship between total outputs and final demands can be formulated as
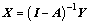 (1)
(1)
where  is the Leontief inverse matrix that shows the total requirements of processes’ production.
is the Leontief inverse matrix that shows the total requirements of processes’ production.
When some industrial processes produce more than one valuable products, energy spending must be partitioned between them in order to accurately reflect their individual contributions to the energy consumptions. These by-products are beneficial to the society and environment as the use of them results in less consumption of virgin materials. Here, the “avoided burden” approach is applied, which means the production of economical valuable by-products could be regarded to replace alternative production of similar functional products. By crediting the by-products with the avoided burden and thus subtracting the avoided burden from the overall energy consumption of a process, the product-specific results can be obtained for main
products [22]. Thus based on the energy conservation conditions, the embodied energy of process main products is equal to the total energy equivalence of all material and energy inputs, subtracting net recovery of by-products, per one unit of main product:
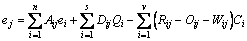 (2)
(2)
Translated into matrix terms, Eq. (2) becomes:
 (3)
(3)
Solving for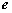
 (4)
(4)
Therefore, by applying what has been called the “impact analysis form” in generalized I-O model of environmental analysis [23], the total energy consumption of all main products production is
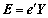 (5)
(5)
Table 1 Conceptual input-output table of production processes
2.2 Structural decomposition analysis of embodied energy
The changes of the energy embodied in various main products between time 0 and t, denoted by △e, can be decomposed using Eq. (6) into the following seven effects in additive form:
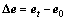
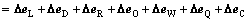 (6)
(6)
where △eL is the Leontief effect caused by changes in Leontief inverse coefficients, which is also interpreted as a technological effect of changes in intermediate inputs structure; △eD is the primary inputs effect due to changes in direct coefficients for primary inputs; △eR is the by-products production effect due to changes in direct coefficients for by-products production; △eO is the by-products inputs effect due to changes in direct coefficients for by-products inputs; △eW is the by-products losses effect due to changes in direct coefficients for unrecovered by-products; △eQ is the primary inputs embodied energy (EE) effect due to changes in embodied energy of primary inputs; and △eC is the by-products EE effect due to changes in embodied energy of by-products.
It has been widely acknowledged in literatures on SDA that there is no unique way to decompose. To overcome the “non-uniqueness problem”, DIETZENBACHER et al [24] proposed to use an average of all possible decomposition forms. In case of  determines (or factors) in multiplication, the number of equivalent decomposition forms is
determines (or factors) in multiplication, the number of equivalent decomposition forms is  and there are only
and there are only  different coefficients for each factor [25]. Therefore, there are 1296 equivalent terms to decompose △e, 4 different coefficients attached to △eD, △eR, △eO, △eQ, △eW and △eQ, 64 different coefficients attached to △eC, and 256 different coefficients attached to △eL. After simplification (e.g. combining like terms), the formulas for each effect are shown as
different coefficients for each factor [25]. Therefore, there are 1296 equivalent terms to decompose △e, 4 different coefficients attached to △eD, △eR, △eO, △eQ, △eW and △eQ, 64 different coefficients attached to △eC, and 256 different coefficients attached to △eL. After simplification (e.g. combining like terms), the formulas for each effect are shown as
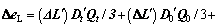

 (7)
(7)

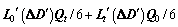 (8)
(8)
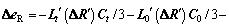
 (9)
(9)

 (10)
(10)

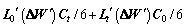 (11)
(11)
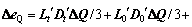
 (12)
(12)
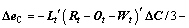

 (13)
(13)
2.3 Hierarchal structural decomposition of total energy consumption changes
It is often happened that some variables can be further disaggregated to a new set of different variables or some variables can be aggregated to a new variable. Therefore, the SDA results may become less convincing if the choice of decomposition model changes the SDA results. For instance, in this work, the embodied energy of main products can be further disaggregated into seven variables. Therefore the final demand effect on total energy consumption would be different and depends on whether the embodied energy is disaggregated.
Inspired by a principle called hierarchical (or nested) decomposition in SDA studies [26-29], the hierarchical SDA combined with D&L method to the changes in total energy consumption has been applied, as shown in Fig. 1.
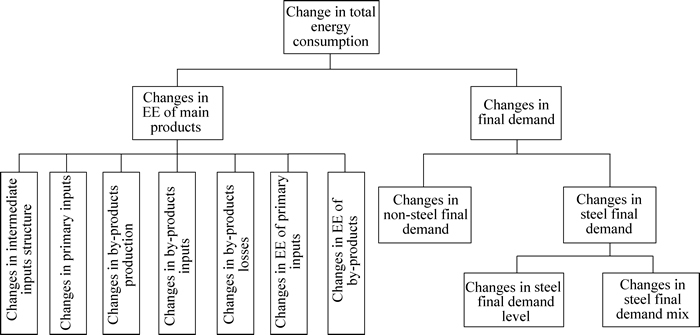
Fig. 1 Hierarchical decomposition structure of changes in total energy consumption
First, the changes in total energy consumption between time 0 and t, denoted by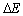 , is decomposed into the following two effects as
, is decomposed into the following two effects as
 (14)
(14)
where △Ee is the main products EE effect caused by changes in embodied energy of all main products, △EY is the final demand effect caused by changes in final demand of main products. To use the average of  different forms, they are calculated as
different forms, they are calculated as
 (15)
(15)
 (16)
(16)
In the second level, △Ee can be further decomposed by substituting △e with Eq. (6). Similarly, △EY can be further decomposed given that the final demand Y can be subdivided into sub-factors. In the case of steel-making processes, the final demand Y is comprised by two parts, namely, the final demand of steel products Ysteel and the final demand of non-steel products Ynon-steel.
 (17)
(17)
Furthermore, the final demand of steel products Ysteel can be expressed as a multiplication of the steel products final demand level (total amount) ysteel-level and the steel products final demand mix Ysteel-mix.
 (18)
(18)
Then, △Y can be further decomposed as follows:
 (19)
(19)
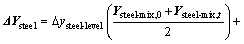
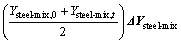 (20)
(20)
For the total energy consumption change 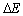 , the expression including all decomposition components as
, the expression including all decomposition components as
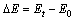
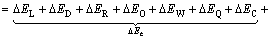
 (21)
(21)
where △EL is the Leontief effect on total energy consumption change (△E) caused by changes in Leontief inverse coefficients, which is also interpreted as a technological effect of changes in intermediate inputs structure; △ED is the primary inputs effect on △E due to changes in primary inputs coefficients; △ER is the by-products production effect on △E due to changes in by-products production coefficients; △EO is the by-products inputs effect on 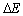 due to changes in by-products inputs coefficients; △EW is the by-products losses effect on △E due to changes in by-products loss coefficients; △EO is the primary inputs EE effect on △E due to changes in EE of primary inputs; △EC is the by-products EE effect on △E due to changes in EE of by-products;
due to changes in by-products inputs coefficients; △EW is the by-products losses effect on △E due to changes in by-products loss coefficients; △EO is the primary inputs EE effect on △E due to changes in EE of primary inputs; △EC is the by-products EE effect on △E due to changes in EE of by-products; 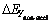 is the non-steel final demand effect on △E due to changes in the final demand of non-steel products;
is the non-steel final demand effect on △E due to changes in the final demand of non-steel products;  is the steel final demand effect on △E due to changes in the final demand of steel products;
is the steel final demand effect on △E due to changes in the final demand of steel products;  is the steel final demand level effect on △E due to changes in the level (total amount) of steel products; and
is the steel final demand level effect on △E due to changes in the level (total amount) of steel products; and  is the steel final demand mix effect on △E due to changes in the mix of steel products final demand. Each effect can be calculated as:
is the steel final demand mix effect on △E due to changes in the mix of steel products final demand. Each effect can be calculated as:
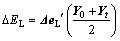 (22)
(22)
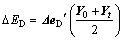 (23)
(23)
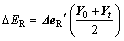 (24)
(24)
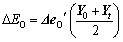 (25)
(25)
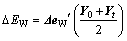 (26)
(26)
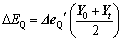 (27)
(27)
 (28)
(28)
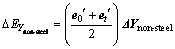 (29)
(29)
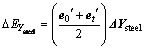 (30)
(30)
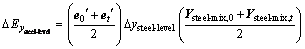 (31)
(31)
 (32)
(32)
2.4 Column-specific and coefficient-specific effects
In the next step, the possibility to further investigate the sub-category effects has been considered with respect to individual changes in disaggregated columns (processes) or elements (coefficients) of various determinants. This would be useful to identify the important changes of process units or individual coefficients between two time periods as an ex-post analysis. Disentangling the aggregated effects into process-level and even coefficient-level results is vital for SDA of production process since the disaggregated effects are more easily interpreted and with a direct relation to a specific technology improvement or inefficiency.
Changes in the Leontief inverse between time 0 and t reflect changes in underlying intermediate inputs coefficients. Thus, by applying the multiplicative identity splitting [1], the changes of Leontief inverse matrix can be formulated as
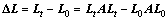
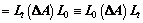 (33)
(33)
Replacing Eq. (33) in Eq. (7) and Eq. (22), the domestic Leontief inverse effect can be transformed to intermediate inputs effect.
Let 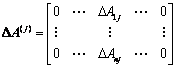 represent the changes in Process j’s intermediate inputs coefficients. Let
represent the changes in Process j’s intermediate inputs coefficients. Let 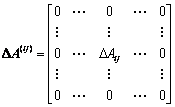 represent the change of the intermediate coefficient Aij. Then
represent the change of the intermediate coefficient Aij. Then
 (34)
(34)
This decomposition of △A can be introduced to Eq. (33), and the resulting expression for △L can be then used in Eq. (7) and Eq. (22). To use the same procedure, the individual process-specific or coefficient-specific effect of other determinants (i.e. D, R, O, W, Q, C and Y) on total energy consumption change can also be obtained.
3 Xiangtan steel plant and data sources
An integrated steel plant named Xiangtan belongs to a leading steel company located in Hunan Province, China. The integrated steel plant includes the following process units: an iron ore sinter plant, a coke making plant, an iron making plant (including four blast furnaces), three basic oxygen furnaces (BOF) with three continuous casting plants, an bar rolling plant, three rod rolling plants, two heavy plate plants, a steam plant, a power plant, an air blast plant, a water plant, an air compression plant and a process gases mixing plant. The above process units are all numbered and listed in Table 2 along with their main products and by-products.
Two types of data are necessary for structural decomposition analysis (SDA) of changes in embodied energy and total energy consumption: 1) a process-level input-output table recording the physical flows (intermediate flows and final demand flows) between the process units of the integrated steel plant, and 2) embodied energy data for the primary inputs and the by-products.
Table 2 Process of Xiangtan steel plant

The data of physical flows are collected from the in-site statistical data and technical reports of Xiangtan steel plant in the year 2011 and 2013. The integrated steel plants exchange materials, fuels and products with numerous other industries through their supply chains. Therefore, both on-site (direct) and upstream (indirect) energy use should be considered from a holistic perspective. As no single source provides all energy data of primary inputs and by-products, several statistical sources have been used. The embodied energy data of various materials and fuel were firstly derived from site investigation reports, a China-based life cycle inventory (LCI) database [30], and a world steel report [31]. Then, other unavailable energy data were derived from a number of published literatures for iron ores [32] and avoided aggregate production by BOF slag [33], supplemented by calculation of avoided cement production by BF slag based on a Chinese cement LCI study [34] and slag treatment data [35]. Avoiding 1 MJ steam production with the same heat quality per MJ steam produced within the site is assumed. Except for electricity and by-product gases, changes of embodied energy of primary inputs and by-products during the 2011 and 2013 are excluded due to the difficulties in collecting accurate data for each specific year.
4 Results and discussion
4.1 SDA of changes in embodied energy
Table 3 shows the main products embodied energy of 2011 and 2013. During 2011 and 2013, the effects of each decomposition factor on embodied energy changes of various main products are also shown in Table 3. For example, the embodied energy of heavy plate 1 decreases from 24.5 to 21.5 MJ/kg during the period. The total decrease of 3 MJ is dominantly contributed from the primary inputs effect with 2.8 MJ, followed by the by-products production effect (0.5 MJ) and the unrecovered by-products effect (0.5 MJ). On the other hand, the Leontief effect and the by-products utilization effect caused a moderate increase of 0.3 MJ and 0.6 MJ, respectively. The △eQ and △eC are not of importance.
The changes of main products embodied energy and the relative contribution of each factor are more clearly observed in Fig. 2. It shows that the embodied energy decreases for most main products except for the blast air, water, compressed air and mixed process gases. The embodied energy of self-generated electricity, heavy plate 1 and cast steel 2 decrease most, with 13%, 11%, and 10% respectively. While the embodied energy of water, blast air and mixed process gases increase most, with 29%, 17% and 10%, respectively.
The primary inputs effect is the major effect contributing to decrease the main products embodied energy. The Leontief effect, on the other hand, is the major effect contributing to increase the embodied energy, except for electricity. This may be caused by some parts of materials bought from outside in 2011 and now become self-produced in 2013. But in total, the unit consumptions of these materials have dropped and the primary inputs effect is larger than the Leontief effect in absolute value for most products. Generally, the by-products production effect and the by-products losses effect contribute to decrease the embodied energy. This is because the steel plant has taken measures on promoting by-products production and reducing its waste (e.g. utilization rate of by-product gases and BF slag has been greatly improved). The by-products inputs effect has contributed to increase the embodied energy due to most process units of the steel plant have consumed more by-products in 2013, except for the heavy plate 2 plant.
Table 3 Structural decomposition analysis of changes in embodied energy of main products during 2011-2013
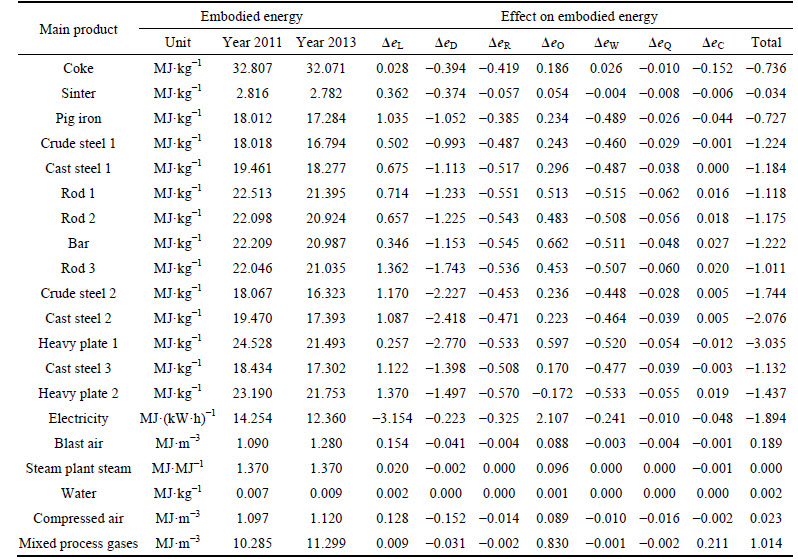
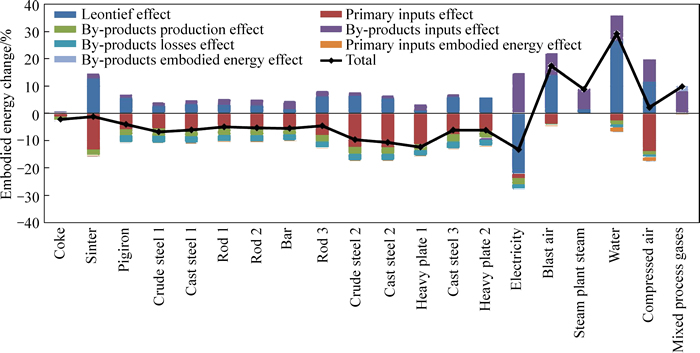
Fig. 2 Contribution of seven effects to changes in main products embodied energy during 2011 and 2013
Both embodied energy effect are negligible because the embodied energy data of primary inputs and by-products have changed little.
4.2 SDA of total energy consumption change
The total energy consumption declined 14.05%, from 169×1015 J in 2011 to 145×1015 J in 2013. Table 4 indicates the effect of changes in all 13 explanatory factors on total energy consumption change of the integrated steel plant between 2011 and 2013. In the first decomposition level, both the main products embodied energy effect and the final demand effect contribute to decrease the total energy consumption by 7.37% and 6.68% respectively. In the second decomposition level, the main products EE effect is further decomposed into seven sub-effects. Among them, the primary inputs effect
is the dominant effect to reduce the total energy consumption by 7.06%, followed by the by-products production effect (-2.28%) and by-products losses effect (-2.14%). On the other hand, the by-products inputs effect and the Leontief effect cause a moderate increase on total energy consumption, of 2.21% and 2.14%, respectively. The primary inputs effect decreases the total energy consumption by 0.23% due to the improvement in efficiency of grid electricity generation and transmission. The by-products embodied energy effect is marginal.
Table 4 Hierarchical structural decomposition analysis of total energy consumption changes between 2011 and 2013

Meantime, the final demand effect can be further divided into the non-steel final demand effect and the steel final demand effect. The latter is further decomposed to the steel final demand level effect and mix effect. The non-steel final demand effect contributes to increase the total energy by 0.37% since a little more non-steel products are made for final demand in 2013. The steel final demand level effect decreases the total energy consumption by 6.82% due to the steel final demand level has decreased from 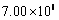 t in 2011 to
t in 2011 to 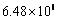 t in 2013. The final demand share of most steel products changes little except for the share of heavy plates 1 and 2. In 2013, the share of heavy plate 1 decreases with 10% whereas the share of heavy plate 2 increases with 9%. However, the embodied energies of heavy plate 1 and 2 are close, which explains why the steel final demand mix effect is small, with only an impact of 0.24% decrease on total energy consumption.
t in 2013. The final demand share of most steel products changes little except for the share of heavy plates 1 and 2. In 2013, the share of heavy plate 1 decreases with 10% whereas the share of heavy plate 2 increases with 9%. However, the embodied energies of heavy plate 1 and 2 are close, which explains why the steel final demand mix effect is small, with only an impact of 0.24% decrease on total energy consumption.
Nevertheless, the above results of aggregated effects only give a general idea of what happened during the analyzed time period but cannot evaluate how changes in technical performance of each process unit influence the total energy consumption. Moreover, they cannot determine the contribution from any specific coefficient change, which is related to a specific technical improvement or inefficiency of production processes. Intrigued by questions such as these, a further decomposition of process-specific and coefficient- specific is required to devise appropriate action lines for each process unit.
4.3 Process specific effects
Figure 3 shows the individual contribution of 20 process units to total energy consumption change regarding 5 related technical effects, namely the intermediate inputs effect, the primary inputs effect, the by-products production effect, the by-products inputs effect, and the by-products losses effect. It shows that the process-specific intermediate inputs effect fluctuates wildly. The changes in intermediate inputs coefficients of process unit 15 (i.e. power plant) decrease the total energy consumption by nearly 3%, while that of process unit 2 (i.e. sinter plant) and process unit 3 (i.e. blast furnace) increases the total energy consumption by about 2%. The process-specific primary inputs effect of all process units generally decreases the total energy consumption. Among them, the primary inputs effect of process units 2, 3 and 10 (basic oxygen furnace 2) decreases the total energy consumption most, by 1.5%- 2%. The process-specific by-products production effects also generally decrease the total energy consumption. The changes in by-products production coefficients of process unit 1 (coke plant) and 3 decrease the total energy consumption most, by about 0.6% due to the productivity improvement in by-products production in those two process units. The by-products inputs effect of process units 15, 17 (steam plant) and 20 (gas processing plant) increases the total energy consumption most, which indicates that these three ancillary process units consumed more energy by-products to produce their energy products. The by-products losses effect of process unit 3 and 15 reduces the total energy consumption by 2% and 0.2%, while that of other process units is negligible. Overall, the above changes in technical coefficients of process units 2, 5, 6, 7, 9 and 16-20 increase the total energy consumption while the othersdecreased it.

Fig. 3 Process-specific effects on total energy consumption change of the integrated steel plant during 2011 and 2013
4.4 Coefficient specific effects
By using the technique introduced in Section 2.4, effects on total energy consumption caused by changes of each direct input-output coefficient can be obtained. Figure 4 maps 82 major coefficients that cause significant increase or decrease on total energy consumption. The effects due to changes in technical coefficients (1), (2), (9), (10), (53) and (73) cause a significant increase over 5% of the total energy consumption change  while the effects due to changes in coefficients (4), (11), (12), (27), (33), (42), (51), (52), (80) and (81) cause a significant decrease over 5% of
while the effects due to changes in coefficients (4), (11), (12), (27), (33), (42), (51), (52), (80) and (81) cause a significant decrease over 5% of 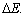 The technical changes of blast furnace decrease the total energy consumption remarkably, which is mainly induced through the changes of coefficients (59), (80) and (81). The recovery rate of blast furnace gas (BFG), reflected by coefficient (80), has been increased from 93.7% to 97.7% in 2011 and 2013 due to that more gas holders and gas pipelines have been built. Moreover, the higher production rate of blast furnace slag (BFS) and the much improved recovery rate of BFS (from 50% to 100%), reflected by coefficients (59) and (81), are achieved because a new cement plant has been built nearby to consume BFS as raw materials. The changes of coefficients (55), (60) and (61) decrease the total energy consumption by
The technical changes of blast furnace decrease the total energy consumption remarkably, which is mainly induced through the changes of coefficients (59), (80) and (81). The recovery rate of blast furnace gas (BFG), reflected by coefficient (80), has been increased from 93.7% to 97.7% in 2011 and 2013 due to that more gas holders and gas pipelines have been built. Moreover, the higher production rate of blast furnace slag (BFS) and the much improved recovery rate of BFS (from 50% to 100%), reflected by coefficients (59) and (81), are achieved because a new cement plant has been built nearby to consume BFS as raw materials. The changes of coefficients (55), (60) and (61) decrease the total energy consumption by  GJ in total, which should be credited to the improved productivity of by-products in the coke plant. The change of coefficient (82) reduces the total energy consumption by
GJ in total, which should be credited to the improved productivity of by-products in the coke plant. The change of coefficient (82) reduces the total energy consumption by 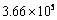 GJ, which should be attributed to the integration of steam pipelines in 2011 and 2013. The changes of coefficients (37)-(39) in total reduce the total energy consumption by
GJ, which should be attributed to the integration of steam pipelines in 2011 and 2013. The changes of coefficients (37)-(39) in total reduce the total energy consumption by 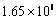 GJ, which should be credited to the improved production efficiency of three basic oxygen furnaces.
GJ, which should be credited to the improved production efficiency of three basic oxygen furnaces.
In 2013, there is a technical problem constantly happened in the sinter plant and blast furnace, which needs a part of the anthracite to be replaced by coke to maintain stable. Moreover, as a consequence of this, more blast air is needed while less oxygen is consumed in blast furnace. Since coke is more energy intensive than anthracite, the energy cost of this problem is huge, as can be seen in coettients (1), (2), (26), (51)-(54), which overall causes an increase of 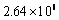 GJ on total energy consumption.
GJ on total energy consumption.
The changes of coefficients (67) and (73) in process unit 15 increase the total energy consumption while the changes of (26), (76) and (77) reduce the total energy consumption. The combined effect of the above five coefficients changes decreases the total energy consumption by  GJ. This is mainly because a new 135 MW steam turbine has been installed consuming by-product gases for electricity production in 2013. Moreover, the new turbine has a higher energy conversion efficiency than previous ones.
GJ. This is mainly because a new 135 MW steam turbine has been installed consuming by-product gases for electricity production in 2013. Moreover, the new turbine has a higher energy conversion efficiency than previous ones.
The technical changes of process unit 17 (steam plant) increase the total energy consumption most by almost 1%. It is clearly shown in Fig. 4 that all three major coefficients changes increase the total energy consumption. This indicates that the declining conversion efficiency of the steam plant has significantly prevented further energy saving, which suggests a major maintenance and retrofit of it.
5 Conclusions
1) Technology improvement and reduced steel final demand are two major reasons for declined total energy consumption in 2011 and 2013. Most embodied energy of intermediate main products have declined, which proves that the energy efficiency of the steel plant has been overall improved. The technical improvements of blast furnace, basic oxygen furnaces and the power plant have contributed mostly in reducing energy consumption.
2) The decreased energy conversion efficiencies of ancillary process units 16-20 have significantly increased the total energy consumption, which suggests that a major retrofit or technical upgrading of them is required.
3) A technical problem in the sinter plant and blast furnace causes a part of the anthracite replaced by coke to maintain stable. This problem increases the total energy consumption greatly and needs to be solved.
4) The by-products production and utilization level have been improved, which greatly reduces the total energy consumption, especially the BFS and BFG. However, with their nearly 100% recovery rate in 2013, further energy reduction from them is small.
5) Moreover, by combining the principle of hierarchical decomposition into the D&L method, a
hierarchical decomposition model for multilevel SDA is obtained. The hierarchical IO-SDA model would provide consistent results, which means the SDA results are the same regardless of the choice of decomposition model. It also reduces the computation effort required. It improves results presentation and usability. The hierarchical IO-SDA model is sufficiently generic to be used not only for decomposition analysis of energy consumption in an integrated steel plant, but also for decomposition analysis of aggregate indicators in other production processes.

Fig. 4 Major coefficient-specific effects on total energy consumption change of integrated steel plant in 2011-2013
References
[1] SU B, ANG B W. Structural decomposition analysis applied to energy and emissions: Some methodological developments [J]. Energy Economics, 2012, 34(1): 177-188.
[2] SHAHIDUZZAMAN M, LAYTON A. Changes in CO2 emissions over business cycle recessions and expansions in the United States: A decomposition analysis [J]. Applied Energy, 2015, 150: 25-35.
[3] SUMABAT A K, LOPEZ N S, YU K D, HAO H, LI R, GENG Y, CHIU A S. Decomposition analysis of Philippine CO2 emissions from fuel combustion and electricity generation [J]. Applied Energy, 2016, 164: 795-804.
[4] CANSINO J M, ROM N R,
N R,  M. Main drivers of changes in CO2 emissions in the Spanish economy: A structural decomposition analysis [J]. Energy Policy, 2016, 89: 150-159.
M. Main drivers of changes in CO2 emissions in the Spanish economy: A structural decomposition analysis [J]. Energy Policy, 2016, 89: 150-159.
[5] ANDREONI V, GALMARINI S. Drivers in CO2 emissions variation: A decomposition analysis for 33 world countries [J]. Energy, 2016, 103: 27-37.
[6] TIMMA L, ZOSS T, BLUMBERGA D. Life after the financial crisis. Energy intensity and energy use decomposition on sectorial level in Latvia [J]. Applied Energy, 2016, 162: 1586-1592.
[7] FERN NDEZ GONZ
NDEZ GONZ LEZ P. Exploring energy efficiency in several European countries. An attribution analysis of the Divisia structural change index [J]. Applied Energy, 2015, 137: 364-374.
LEZ P. Exploring energy efficiency in several European countries. An attribution analysis of the Divisia structural change index [J]. Applied Energy, 2015, 137: 364-374.
[8] YUAN B, REN S, CHEN X. The effects of urbanization, consumption ratio and consumption structure on residential indirect CO2 emissions in China: A regional comparative analysis [J]. Applied Energy, 2015, 140: 94-106.
[9] LAN J, MALIK A, LENZEN M, MCBAIN D, KANEMOTO K. A structural decomposition analysis of global energy footprints [J]. Applied Energy, 2016, 163: 436-451.
[10] SHAO S, LIU J, GENG Y, MIAO Z, YANG Y. Uncovering driving factors of carbon emissions from China’s mining sector [J]. Applied Energy, 2016, 166: 220-238.
[11] GAMBHIR A, TSE L K C, TONG D, MARTINEZ-BOTAS R. Reducing China’s road transport sector CO2 emissions to 2050: Technologies, costs and decomposition analysis [J]. Applied Energy, 2015, 157: 905-917.
[12] LIU Z, GENG Y, ADAMS M, DONG L, SUN L, ZHAO J, DONG H, WU J, TIAN X. Uncovering driving forces on greenhouse gas emissions in China’ aluminum industry from the perspective of life cycle analysis [J]. Applied Energy, 2016, 166: 253-263.
[13] KARMELLOS M, KOPIDOU D, DIAKOULAKI D. A decomposition analysis of the driving factors of CO2 (Carbon dioxide) emissions from the power sector in the European Union countries [J]. Energy, 2016, 94: 680-692.
[14] ALISES A, VASSALLO J M, AYMERICH M. Comparison of road freight transport trends in Europe: Results of an input-output structural decomposition analysis [C]// Transportation Research Board 94th Annual Meeting. Washington, D.C.: TRB, 2015: 1-15.
[15] TAN X, DONG L, CHEN D, GU B, ZENG Y. China’s regional CO2 emissions reduction potential: A study of Chongqing city [J]. Applied Energy, 2016, 162: 1345-1354.
[16] LU Q, YANG H, HUANG X, CHUAI X, WU C. Multi-sectoral decomposition in decoupling industrial growth from carbon emissions in the developed Jiangsu Province, China [J]. Energy, 2015, 82: 414-425.
[17] WANG Z, LIU W. Determinants of CO2 emissions from household daily travel in Beijing, China: Individual travel characteristic perspectives [J]. Applied Energy, 2015, 158: 292-299.
[18] XIA X H, HU Y, ALSAEDI A, HAYAT T, WU X D, CHEN G Q. Structure decomposition analysis for energy-related GHG emission in Beijing: Urban metabolism and hierarchical structure [J]. Ecological Informatics, 2015, 26(1): 60-69.
[19] ZHI Y, YANG Z, YIN X A, HAMILTON P B, ZHANG L. Evaluating and forecasting the drivers of water use in a city: Model development and a case from Beijing [J]. Journal of Water Resources Planning and Management, 2015, 142(1): 04015042.
[20] LIN X, POLENSKE K R. Input-output modeling of production processes for business management [J]. Structural Change and Economic Dynamics, 1998, 9(2): 205-226.
[21] ALBINO V, DIETZENBACHER E, K HTZ S. Analysing materials and energy flows in an industrial district using an enterprise input–output model [J]. Economic Systems Research, 2003, 15(4): 457-480.
HTZ S. Analysing materials and energy flows in an industrial district using an enterprise input–output model [J]. Economic Systems Research, 2003, 15(4): 457-480.
[22] JUNG J, von der ASSEN N, BARDOW A. Comparative LCA of multi-product processes with non-common products: A systematic approach applied to chlorine electrolysis technologies [J]. The International Journal of Life Cycle Assessment, 2013, 18(4): 828-839.
[23] MILLER R E, BLAIR P D. Input-output analysis: Foundations and extensions [M]. New York: Cambridge University Press, 2009.
[24] DIETZENBACHER E, LOS B. Structural decomposition techniques: sense and sensitivity [J]. Economic Systems Research, 1998, 10(4): 307-324.
[25] SEIBEL S. Decomposition analysis of carbon dioxide-emission changes in Germany-Conceptual framework and empirical results [J]. Luxembourg: Office for Official Publications of the European Communities, European Communities, 2003.
[26] SONIS M, HEWINGS G J, GAZEL R. The structure of multi-regional trade flows: Hierarchy, feedbacks and spatial linkages [J]. The Annals of Regional Science, 1995, 29(4): 409-430.
[27] DIETZENBACHER E, LOS B. Structural decomposition analyses with dependent determinants [J]. Economic Systems Research, 2000, 12(4): 497-514.
[28] KAGAWA S, INAMURA H. A structural decomposition of energy consumption based on a hybrid rectangular input-output framework: Japan’s case [J]. Economic Systems Research, 2001, 13(4): 339-363.
[29] WU J H, CHEN Y Y, HUANG Y H. Trade pattern change impact on industrial CO2 emissions in Taiwan [J]. Energy Policy, 2007, 35(11): 5436-5446.
[30] LIU X, WANG Hong-tao, CHEN J, HE Q, ZHANG H, JIANG R, CHEN X. Method and basic model for development of Chinese reference life cycle database of fundamental industries [J]. Acta Scientiae Circumstantiae, 2010, 30(10): 2136-2144.
[31] WORLDSTEEL. CO2 emissions data collection (User Guide, version 6) [R]. Brussels: Worldsteel Association, 2012.
[32] NORGATE T, HAQUE N. Energy and greenhouse gas impacts of mining and mineral processing operations [J]. Journal of Cleaner Production, 2010, 18(3): 266-274.
[33] MARINKOVI S, RADONJANIN V,
S, RADONJANIN V,  M, IGNJATOVI
M, IGNJATOVI I. Comparative environmental assessment of natural and recycled aggregate concrete [J]. Waste management, 2010, 30(11): 2255-2264.
I. Comparative environmental assessment of natural and recycled aggregate concrete [J]. Waste management, 2010, 30(11): 2255-2264.
[34] JIANG R, WANG H, ZHANG H, CHEN X. Life cycle assessment of cement technologies in China and recommendations [J]. Acta Scientiae Circumstantiae, 2010, 30(11): 2361-2368.
[35] CHEN C, HABERT G, BOUZIDI Y, JULLIEN A, VENTURA A. LCA allocation procedure used as an incitative method for waste recycling: An application to mineral additions in concrete [J]. Resources, Conservation and Recycling, 2010, 54(12): 1231-1240.
(Edited by FANG Jing-hua)
Cite this article as: LIU Xiao-jun, LIAO Sheng-ming, RAO Zheng-hua, LIU Gang. A process-level hierarchical structural decomposition analysis (SDA) of energy consumption in an integrated steel plant [J]. Journal of Central South University, 2017, 24(2): 402. DOI: 10.1007/s11171-017-3442-3.
Foundation item: Project(2012GK2025) supported by Science-Technology Plan Foundation of Hunan Province, China; Project(2013zzts039) supported by the Fundamental Research Funds for Central South University, China
Received date: 2016-07-21; Accepted date: 2016-12-15
Corresponding author: LIAO Sheng-ming, Professor, PhD; Tel: +86-731-88836936; E-mail: smliao@csu.edu.cn

