DOI： 10.11817/j.issn.1672-7207.2019.08.008

循环扭转剪切下圆筒内硬球颗粒的致密化行为

欧阳鸿武¹,雷刚¹,唐昕¹,孟力平²

（1. 中南大学 机电工程学院，湖南 长沙，410083；

2. 中南大学 材料科学与工程学院，湖南 长沙，410083）

摘要:基于圆筒内硬球颗粒的致密化过程涉及应力传递与堆积结构的耦合作用，是颗粒介质研究中的一个难点问题，为此，采用MTS 858 Mini Bionix II型力学性能测试仪，通过改变压力、颗粒粒径、剪切速率等参数，对循环扭转剪切作用下的致密化行为进行实验研究。研究结果表明：颗粒介质致密化过程表现为快速致密和缓慢致密2个阶段，体积分数的演化过程满足双指数项关联函数，即（其中，为系统初始体积分数，A₁和A₂为拟合系数，t₁和t₂分别为快速和缓慢致密过程的特征时间）；系统经历快速堵塞过程后，进入颗粒缓慢重排过程；在循环剪切过程中，颗粒体积分数的涨幅在体积分数达到0.604时发生由降转升的转变；增大压力、粒径与圆筒直径之比（d/D）以及剪切速率均有利于提高致密化程度，循环扭转剪切作用比纯剪切和垂直振动作用的致密化效率更高。

关键词:硬球颗粒；循环扭转剪切；致密化；转变行为

中图分类号:TB30    文献标志码:A     文章编号:1672-7207（2019）08-1816-08

Compaction behaviors of hard spherical granules in cylinder subject to cyclic torsional shear

OUYANG　Hongwu¹, LEI　Gang¹, TANG　Xin¹, MENG　Liping²

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China；

2. School of Materials Science and Engineering, Central South University, Changsha 410083, China)

Abstract: Considering that the coupling of stress transmission and structural organization during the compaction process of hard spheres in a cylinder is difficult to be described, a series of experiments were carried out to study this process, using the MTS 858 Mini Bionix II type mechanical property tester. The compaction was studied as a function of confining pressure, particle size and shear rate. The results show that the compaction process is characterized by two time scales, i.e. t₁ and t₂, volume fraction satisfies , where is the initial volume fraction, A₁ and A₂ are fitted coefficients. t₁ and t₂ are characteristic time of rapid and slow compaction process, respectively. After the system goes through the state of rapid compaction, it enters a creep regime involving slow rearrangement of particles. The increase of the volume fraction undergoes a transition from decrease to increase when the volume fraction reaches 0.604. The rate of compaction and the final volume fraction increase with the increase of the pressure, the ratio of sphere size to cylinder diameter(d/D) and shear rate. Compaction is more efficient subject to cyclic torsional shear than that pure shear and vertical vibration.

Key words: hard spherical granules; cyclic torsional shear; compaction; transition behavior

颗粒堆积状态和力学特性在工程中影响粉体、制药、化工及物流等领域的生产过程和产品质量稳定 性^[1-2]，在物理和数学等领域，圆筒内硬球颗粒介质堆积问题是研究的热点和难点。在致密化过程中，颗粒介质表现出临界相变行为、剪切堵塞、剪切膨胀等特性，但仍不能用已成熟的传统热力学和流体力学方法来描述这些特性^[3]。BERNAL等^[4]提出随机致密堆积(RCP)的概念，并对液体分子堆积结构进行了描述；SCOTT等^[5-6]将颗粒介质的体积分数作为系统的基本参数，进一步提出与N^-1/3呈线性关系(其中，N为颗粒数目)，通过实验结果推导出无限个颗粒(或无限空间内)的随机致密堆积密度和随机松散堆积密度，并且通过实验验证了和分别为0.637和0.601。TORQUATO等^[7]发现颗粒介质受堵塞结构限制存在一个最无序堆积状态，即最大随机堵塞状态(MRJ)。尽管状态MRJ和RCP下的体积分数均 为0.64，但它们的物理意义各不相同，至今仍未统一起来。METHA等^[8]基于统计力学观点，以圆筒内颗粒介质的堆积状态为原型，提出假设：给定体积中颗粒堆积结构的每种几何构型出现的概率相同，并将颗粒介质的体积V对应于能量，压缩性X为颗粒介质的温度(X=0对应于最致密状态，X=∞对应于最稀疏状态)，定义，其中S为颗粒介质构型熵。这一假设后来得到验证^[9]，可压缩性X可以有效地用于表征颗粒介质致密化程度和演化过程特征。多年来，人们对圆筒内颗粒介质的致密化行为和特征进行了深入研究。KNIGHT等^[10]在实验中对颗粒介质施以垂直方向振动激励，结果表明颗粒体积分数呈对数增长规律：。这是一个慢动力学演化过程，采用停车场模型、阻挫晶格气体模型以及具有短程动力约束的一维晶格模型可有效解释这一动力学过程。NICOLAS等^[11]设计了纯剪切实验，发现等剪切幅度循环致密化过程是一个慢动力学过程，而变剪切幅度是与慢过程无关的快动力学过程。这些研究揭示出颗粒介质的丰富特性，如记忆效应、棘轮效应、剪切膨胀效应等，圆筒内单向扭转剪切作用下颗粒介质表现出的特性更加突出：靠近圆筒中心的团簇处于堵塞态，远离圆筒中心的颗粒则在剪切应力下发生运动，处于屈服态，这2个不同区域的力网结构和物性均存在差异^[12]。最外层和次外层之间因几何结构的冲突必然存在孔隙，孔隙的径向分布函数在(6~7) d范围内呈震荡衰减(其中，d为颗粒粒径)^[13]。为了分析此现象，本文作者搭建循环扭转剪切实验平台，以钢珠为颗粒样本，测试硬球颗粒介质在圆筒内的循环扭转剪切致密化行为，以探明致密化过程的特征及影响因素。

1 实验

实验采用内腔直径D=84 mm的圆筒，选用粒径d分别为1.5，2.0和3.0 mm的轴承钢珠，所用材料及性质如表1所示。实验装置及原理示意图如图1所示。

表1　圆筒和钢珠的力学性质

Table 1　Mechanical properties of cylinder and steel ball

图1　实验装置及原理示意图

Fig. 1　Schematic diagram of experimental setup and principle

在实验过程中，将N个钢珠称质量后(天平精度为10^-4 g)随机倒入圆筒中，摇匀并轻轻拍打(用镊子搅匀后再用勺子铺平)，随后置于压盘之下，将压盘和圆筒分别用上、下2个夹具牢固地固定在MTS 858 Mini Bionix II型力学性能测试仪上。垂向上，通过压盘对颗粒介质施加恒定的压力F，压盘水平扭转时的剪切速率为ω(顺时针为正，逆时针为负，见图1(b))。为充分消除颗粒介质添加过程中产生的影响或为了保证初始条件的一致性，在每次循环扭转剪切开始前，以恒定的速率(100 N/s)加载至额定压力F，获得初始体积分数，随后开始循环扭转剪切实验，实验过程持续120 s。实验方案以压力F、颗粒粒径d以及剪切速率ω为变量，组合成相应的实验体系，对颗粒的致密化行为特征开展系统研究。记录圆筒内颗粒堆积高度H即体积的变化情况，测量精度为1 μm。

本文从近100组实验数据中选取几组有代表性的实验数据，其实验方案MO1，MO2和MO3如表2所示，以此对圆筒内颗粒介质循环扭转剪切作用下的致密化过程进行表征。表2中，方案MO1和MO2分别表示粒径为1.5 mm和3.0 mm，保持剪切速率(10π rad/s)不变，仅改变压力时的致密化过程；方案MO3表示粒径为2.0 mm，压力为3 kN，仅改变剪切速率(分别为0.1π，0.2π，2.0π和10.0π rad/s)的致密化过程。

表2　实验方案

Table 2　Experimental schemes

2 结果与分析

2.1　致密化过程的基本特征

体积分数是表征颗粒介质致密化行为的参数，表征颗粒介质的宏观特性，通过实验获得。通过实验过程中记录得到的颗粒堆积高度H可以获得致密化过程中体积分数。的计算公式为

(1)

式中：d为颗粒粒径，mm；N为颗粒数目，个；D为圆筒内径，mm；H(t)为颗粒堆积高度，mm。体积分数及扭矩T在3个时间段的涨落见图2。根据式(1)得到实验MO1中1 kN压力下相应的体积分数，如图2(a)所示。下文中若无另外说明，则显示的实验结果均为方案MO1中1 kN实验条件下的结果。

图2　体积分数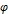及扭矩T在3个时间段的涨落

Fig. 2　Fluctuation of volume fraction 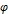and torque T in three time slots

从图2(a)可见：整体上呈单调增长趋势，从0.591增加至0.612。从图2(b)～(e)可见：虽然剪切方向一正一反(顺时针方向为正，逆时针方向为反)，但单向剪切(顺时针或逆时针)时颗粒的体积分数基本都经历了先升高后降低的过程(都会出现波峰和波谷)，表明颗粒堆积体积经历了先收缩后膨胀2个状态。

2.1.1　转变行为　

通过实验结果可以发现堆积系统在剪切作用下的致密化过程存在2个不同的阶段，分别为快速致密阶段(Stage 1)和缓慢致密阶段(Stage 2)，见图3(a)。第1阶段为迅速增长状态，此时小于0.604；第2阶段超过0.604，每次循环中，颗粒体积分数出现缓慢的阶段性增长，表明致密化过程进入缓慢的颗粒重排阶段。图3(a)中，致密化过程的拟合采用双指数项关联函数效果最好，拟合公式为

图3　致密化过程中的转变行为

Fig. 3　Transition behavior during compaction

(2)

式中：为系统初始体积分数；A₁和A₂为拟合系数；t₁和t₂分别为快速和缓慢致密过程的特征时间。该拟合式的基本特点是当t→∞时，的最大值为，A₁和A₂三者之和。图3(a)中的实验拟合结果为

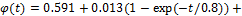
(3)

在此实验条件下，堆积系统获得的最致密体积分数0.613，可见实验时间不会影响最终密度的获得。式(3)中，2个特征时间分别为t₁=0.8 s，t₂=81.4 s，对应于系统一快一慢这2个致密化阶段。

从图2(b)，(c)和(d)可以看出总是存在波动，本文利用来表征颗粒堆积系统的结构涨落和转变，如图3(b)所示(其中，为每次波动中的最小值)。图3(b)中的拟合式为

(4)

式(4)中，拟合曲线的斜率在0.604处发生改变。这与文献[14]中所表述的在0.60左右发生转变具有高度一致性，说明此时系统发生的转变为连续转变。在转变之前，一直下降，而在转变之后，呈上升趋势。但在每次循环中，也会存在明显涨落和波动，导致堆积系统出现间歇性的致密化行为。由此可见：在颗粒介质的致密化过程中，要使堆积系统达到更高的堆积密度，发生转变是必要条件。

2.1.2　致密化过程中的剪切堵塞　

图4所示为颗粒介质的堵塞相图^[15]，其中，为非剪切堵塞体积分数，为堵塞体积分数。当时，在剪切作用下颗粒介质将会发生剪切堵塞；在致密化过程中，颗粒堆积系统因受剪切而发生膨胀，导致降低，系统从剪切堵塞态转变到非堵塞态，因剪切方向变化而发生收缩，此时增加，从而使系统回到剪切堵塞状态。堆积系统存在2种力学响应模式：一种是在低密度、低应力时，由于剪切堵塞导致密度下降而应力τ上升；另一种是当大于0.604时，图4中指向左方箭头的起点穿越线，当系统处于堵塞态时，剪切仍旧导致体积膨胀，但应力减小，因此，是相变点，也是一个随堆积结构演化的临界点，但由于堵塞态颗粒介质的内部存在各项异性，又使颗粒介质不同于平常的固体和液体^[16-17]。

图4　颗粒介质的堵塞相图^[15]

Fig. 4　Jamming phase diagram of granular matter

在致密化过程中，不仅系统的体积分数不断增加，而且堵塞体积分数会随着系统体积分数的增加而发生相应变化，即堵塞体积分数是1个动态变量，图4很好地说明了这一点。根据文献[18]，堵塞体积分数作为堵塞相图中的补充变量能够表征颗粒的堆积状态，引入能够阐明颗粒介质循环剪切致密化过程中非常复杂的状态转变^[15]。在循环扭转剪切过程中，颗粒介质的堵塞体积分数与颗粒介质的体积分数有密切关系：体积分数增大可能是剪切过程中增大的结果，因此，颗粒介质在循环扭转剪切作用下的致密化受到堵塞体积分数的影响。

2.2　压力、粒径和剪切速率对致密化过程的影响

2.2.1　压力和粒径的影响　

图5(a)所示为粒径d=1.5 mm的钢珠堆积系统在压力为1，2和3 kN时(即MO1方案)的致密化曲线，粒径d=3.0 mm的致密化实验过程(即MO2方案)与图 5(a)的相似，最终的颗粒体积分数见表3。从图5(a)可见：在不同压力下，颗粒介质的体积分数演化的趋势具有相似性，致密化程度存在一定差异。可见：压力越大，颗粒介质致密化程度越高。

图5　压力和剪切速率对致密化过程和结果的影响

Fig. 5　Effects of pressure and shear rate on process and results of compaction

表3　不同压力下的体积分数及特征时间t₁和t₂

Table 3　Volume fraction at different pressures and characteristic time t₁ and t₂

2.2.2　剪切速率的影响　

在垂直振动致密化的实验研究中，颗粒介质的动力学过程极度缓慢，一般要历经数千次振动循环，颗粒体积分数才能达到其稳定值。JOSSERAND等^[19]在同一次实验进程中突然改变Γ(Γ为振动强度，即振动加速度幅值与重力加速力之比)，使Γ由大变小(Γ₁＞Γ₂)以及由小变大(Γ₁＜Γ₂)，来研究堆积密度的响应。本文则通过改变循环扭转剪切实验中的剪切速率ω考察其对致密化行为的影响。

选定粒径d=2.0 mm的颗粒，在F=3 kN下，以4个不同的剪切速率ω(0.1π，0.2π，2.0π和10.0π rad/s)分别进行实验(即方案MO3)。首先从低频0.1π rad/s开始，每个剪切速率下循环扭转剪切的实验时间均为120 s，剪切停止时系统卸压，随即以100 N/s的速度加载至额定压力3 kN，提高剪切速率后继续进行实验，实验结果如图5(b)所示。结果表明：剪切速率的变化在密度较低时对致密化过程起增强作用；当密度达到饱和密度后剪切速率的影响减弱，直至末期影响很小，结合图4所示堵塞相图的颗粒介质密度演化机制可知：进入饱和状态后，堆积结构涨落频率很大，但几乎无法再进一步致密化。这是由于剪切堵塞的区域越来越小，剪切层厚度越来越小，堆积结构发生变形的能力逐渐减小，除非经历1次相变，否则系统处于“吸引状态”将不会得到改观，这与文献[11]中的纯剪切致密化行为形成了明显差异。

2.2.3　压力、粒径和剪切速率对致密化行为的影响机制

SONG等^[20]通过研究发现，当压力在一定范围内增加时，会导致颗粒间几何接触数Z_g增加，随体积分数增大，颗粒间的几何接触数Z_g的变化满足

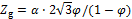(5)

式中：α=1.1。式(5)表明当体积分数逐渐增加时，几何接触数逐渐增加及颗粒间重新排列，因此，压力越大，颗粒介质的致密化程度就越高。

在同一圆筒容器中，不同粒径颗粒堆积导致密度不同，并且径向和周向的致密化过程也会不同。从结构上看，周向的致密化速率快，而径向的致密化速率变化缓慢，径向的致密化速率只有周向的1/‰。小粒径颗粒的摩擦力相对大粒径颗粒的摩擦力要大一些，导致最终密度存在差异，而致密化过程差异不大。

在一般情况下，硬球颗粒介质有3种致密途径：1) 非拥挤式增长，这种方式无需打乱现有颗粒的排列；2) 局部拥挤式增长，即仅1个颗粒需要重排； 3) 全域拥挤式增长，即涉及2个颗粒需要重排以容纳1个新颗粒进入。不同的剪切速率将导致不同的致密方式：在低频剪切下，颗粒的致密化速度较低，但系统在每个循环中有足够的时间进行弛豫，参与剪切变形的颗粒团簇多，属于全域拥挤式增长模式，因此，密度的涨落明显，每个循环中密度增大幅度大，但增大速率较低；高频剪切时，循环周期与密度弛豫时间相差较大，颗粒还没来得及发生大的剪切变形，就被迫承受另一个方向的剪切应力，而且能够参与变形的颗粒层仅处于与压盘接触的表面少数几层，即使颗粒的堆积高度H＞7d(d为颗粒粒径)，能够发生剪切变形的高度也不会超过7d，此时，致密化行为为局部拥挤式增长方式，密度波动不明显，在此剪切速率下，密度也不会提高太多(见图5(b))。因此，角速率影响了致密化过程中颗粒重排的方式，主导了堆积密度的涨落幅度。当密度达到一定程度后，剪切速率的影响逐渐降低。因为有剪切层(厚度为h_shear)和蠕变层(厚度为h_creep)的共存(见图1(b))，所以，剪切速率对致密化的影响可能比所表述的情况更复杂。

当颗粒介质受剪切作用时，一般剪切层能够形成的力链长度为(6~7)d，即h_shear=7d；当颗粒数目N较小，堆积系统高度不足7d时，几乎每一层颗粒都会在剪切应力下发生运动，此时，弛豫过程相当短，而且密度波动幅度相当大；当颗粒数目N较多时，堆积系统的高度足够大；当堆积系统高度超过7d时，圆筒底部区域的颗粒特征不同于剪切层，此区域称之为蠕变层，见图1(b)中的底部颗粒层。在一定高度范围内，2个区域共存时的堆积密度相对于只有剪切区时较高，波动幅度也更小，因此，颗粒数目N的变化引起堆积系统质的改变，在一定程度上决定了系统2个不同的特征时间。总体来说，致密化过程中2个区域相互协调，整体密度处于高、低2个密度之间，但由于存在剪切层，会使整个系统的密度略微降低，不过剪切过程有利于颗粒重排，能有效促进致密化，正因为如此，循环扭转剪切下的致密化比纯剪切和垂直振动下的致密化能获得更快的致密化过程和更高的体积分数，见图5(b)。

3 讨论

3.1　致密化过程中的2个特征时间

致密化呈现出快、慢2个不同阶段，原因可能是剪切层和蠕变层颗粒存在不同弛豫过程。CORWIN等^[12]的研究表明，堆积系统中靠近圆筒中心的颗粒处于堵塞状态，而远离圆筒中心的颗粒则在剪切应力下发生运动。与此同时，在不同高度上也会存在微妙区别：表层的颗粒(厚度为h_shear)处于剪切屈服状态(密度较低)，对应于单个颗粒运动的特征时间，弛豫时间极短，很快就达到极限密度，而剪切层之下的颗粒(厚度为h_creep)则处于缓慢蠕变状态(密度较高)，对应于颗粒团簇运动的特征时间，因此，需要更长的时间达到稳态密度。在快速阶段，颗粒介质在压、剪作用下发生快速堵塞行为；在慢速阶段，剪切层的厚度不断减小，且蠕变层则更多地发生颗粒重排。

通过对比分析图5(b)中不同作用方式致密化曲线发现，循环扭转剪切与纯剪切和垂直振动作用下的致密化过程存在差异，表现为前者的致密化过程中存在2个特征时间，可以更快地获得稳定密度，并且快致密阶段几乎在3 s内就能完成，同时可以通过压力来控制致密化程度，而纯剪切和垂直振动下的密度弛豫过程只有1个特征时间，过程也相对平缓。在方案MO3的实验时长(600 s)内，相比于纯剪和振动致密化，循环扭转剪切作用下得到的体积分数结果分别高1.25%和3.53%。因此，在实际生产和日常生活中，要使颗粒堆积系统更快获得较高的致密化程度，循环扭转剪切是一种更好的选择。

3.2　记忆效应和颗粒数目对致密化的影响

实验中压盘先正向(顺时针)扭转，随后反向(逆时针)扭转，第1个剪切循环就给堆积系统留下了“记忆”，以后的每次循环都或多或少地受到第1个循环的影响，导致颗粒介质的状态、物性与变形过程的历史、作用方式相关。尽管有记忆效应存在，颗粒介质仍然能够随着时间推移“忘记”其初始状态，此时，系统处于一种临界性特征，即所谓的临界松弛(critical slowing down)^[21]。致密化过程(某一段时间内)在某种程度上就是记忆的消除过程，式f(t)=f(0)·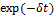表明系统中的特征时间为。记忆效应逐渐消除之后颗粒堆积系统逐渐进入与外载荷动态平衡的状态，表现出颗粒介质对外载荷自适应的能力，在一定程度上反映了系统致密化的过程。

研究表明，少量颗粒数目的变化也将引起颗粒堆积结构和密度的变化。因此，在围限条件下，颗粒数目N对体积分数有直接影响。假如以1D模型为例，10颗钢珠(围限条件是长度为10d)，加入1个钢珠，在无压力情况下，多出的1个颗粒位于第2层，当施加一定压力时，颗粒的堆积形成起伏，显然，堆积的高度H降低对颗粒体积分数产生较大影响。而加入2个钢珠后，出现类似的情况。从二维的角度分析，情况更复杂多变，堆积结构变化更具多样性。由此可见：在围限情况下，适度的压力将使得颗粒堆积结构产生变化，相应地，在低层数情况下，对结构的影响较明显。

3.3　可压缩性的演化

通过以上分析发现利用堵塞体积分数可以揭示相变点附近的现象和复杂的作用机制。表明系统已经处于“吸引状态)”，系统经历相变之后进入了一个新的状态，因此，是连续转变过程中的1个状态参数，记录和调控了转变的过程。所以，致密化过程采用来表述，能够更好地表述颗粒介质的物性和状态协同转变。体积分数与堵塞体积分数的差值表征堆积系统的状态，与可压缩性X的定义(X=V/S，V为体积，S为构型熵)类似。

离散颗粒的力学特征与连续介质的描述存在紧密联系^[22]，因此，采用可压缩性X表征颗粒介质的统计特征是有效的。NOWAK等^[23]将可压缩性X与体积平均方差联系起来，建立如下数学关系式：

(6)

式中：V_SS为稳态体积(V_SS=，为稳定状态体积分数)；X₁和X₂分别表征始和结束时刻的可压缩性；λ为类似于玻尔兹曼常数的参数；< >表示取平均值。由式(6)可进一步推导得

(7)

从方案MO3得到的大量数据可以计算出拟合关系式：

故

(8)

将λX视为整体，它与的关系见图6，通过计算得到(1/X₁-1/X₂)/λ=-0.347，其变化趋势与图2(a)所示趋势恰好相反，但都呈现单调变化趋势(密度单调增加，而可压缩性单调降低)。图6表明可压缩性和密度之间存在非线性对应关系。

图6　可压缩性与稳态体积分数的关系

Fig. 6　Relationship between compactivity and steady-state volume fraction

4 结论

1) 圆筒中硬球颗粒介质在循环扭转剪切作用下，致密化过程经历全域快速堆积和剪切层缓慢蠕变2个阶段，体积分数的演化满足双指数项关联函数。在致密化过程中，当密度达到0.604之前表现为快速致密化特征，达到0.604之后则表现为缓慢致密化特征。

2) 压力、粒径和剪切速率对致密化过程和结果有明显影响。增大压力、粒径和剪切速率，系统致密化程度相应提高，可压缩性X随之逐渐下降，并满足(1/X₁-1/X₂)/λ=-0.347。

3) 与纯剪切和垂直振动作用下的致密化过程相比，圆筒内硬球颗粒介质在循环扭转剪切作用下可以更快地达到相应平衡状态下的密度，这为硬球颗粒介质快速致密化提供了新的方法和途径。

参考文献：

[1] ZAMPONI F. Mathematical physics: packings close and loose[J]. Nature, 2008, 453(7195): 606-607.

[2] TORQUATO S, STILLINGER F H. Jammed hard-particle packings: from kepler to bernal and beyond[J]. Reviews of Modern Physics, 2010, 82(3): 2633-2672.

[3] 陆坤权, 刘寄星. 颗粒物质[J]. 物理, 2004, 33(10): 713-721.

LU Kunquan, LIU Jixing. Particle matter[J]. Physics, 2004, 33(10): 713-721.

[4] BERNAL J D, FOWLER R H. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions[J]. Journal of Chemical Physics, 1933, 1(8): 515-548.

[5] SCOTT G D. Packing of spheres: packing of equal spheres[J]. Nature, 1960, 188(4754): 908-909.

[6] SCOTT G D, KILGOUR D M. The density of random close packing of spheres[J]. Journal of Physics D: Applied Physics, 1969, 2(6): 863-866.

[7] TORQUATO S, TRUSKETT T M, DEBENEDETTI P G. Is random close packing of spheres well defined?[J]. Physical Review Letters, 2000, 84(10): 2064-2067.

[8] MEHTA A, EDWARDS S F. Statistical mechanics of powder mixtures[J]. Physica A: Statistical Mechanics and Its Applications, 1989, 157(3): 1091-1100.

[9] BAULE A, MORONE F, HERRMANN H J, et al. Edwards Statistical Mechanics for Jammed Granular Matter[J].Reviews of Modern Physics, 2018, 90(1): 2-12.

[10] KNIGHT J B, FANDRICH C G, LAU C N, et al. Density relaxation in a vibrated granular material[J]. Physical Review E: Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1995, 51(5): 3957-3963.

[11] NICOLAS M, DURU P, POULIQUEN O. Compaction of a granular material under cyclic shear[J]. The European Physical Journal E, 2000, 3(4): 309-314.

[12] CORWIN E I, JAEGER H M, NAGEL S R. Structural signature of jamming in granular media[J]. Nature, 2005, 435(7045): 1075-1078.

[13] REIMANN J, VICENTE J, BRUN E, et al. X-ray tomography investigations of mono-sized sphere packing structures in cylindrical containers[J]. Powder Technology, 2017, 318: 471-483.

[14] MTAYER J F, SUNTRUP D J III, RADIN C, et al. Shearing of frictional sphere packings[J]. EPL(Europhysics Letters), 2011, 93(6): 64003.

[15] BI Dapeng, ZHANG Jie, CHAKRABORTY B, et al. Jamming by shear[J]. Nature, 2011, 480(7377): 355-358.

[16] 彭政, 陆坤权, 厚美瑛. 阻塞态颗粒介质的慢速阻力[J]. 物理学报, 2009, 58(9): 6566-6572.

PENG Zheng, LU Kunquan, HOU Meiying. Slow drag in jammed granular medium[J]. Acta Physica Sinica, 2009, 58(9): 6566-6572.

[17] 孙其诚, 王光谦. 静态堆积颗粒中的力链分布[J]. 物理学报, 2008, 57(8): 4667-4674.

SUN Qicheng, WANG Guangqian. Force distribution in static granular matter in two dimensions[J]. Acta Physica Sinica, 2008, 57(8): 4667-4674.

[18] LUDING S. Granular matter: so much for the jamming point[J]. Nature Physics, 2016, 12(6): 531-532.

[19] JOSSERAND C, TKACHENKO A V, MUETH D M, et al. Memory effects in granular materials[J]. Physical Review Letters, 2000, 85(17): 3632-3635.

[20] SONG Chaoming, WANG Ping, MAKSE H A. A phase diagram for jammed matter[J]. Nature, 2008, 453(7195): 629-632.

[21] MUOZ M A. Colloquium: Criticality and dynamical scaling in living systems[J]. Reviews of Modern Physics, 2018, 90(3): 5-17.

[22] POORSOLHJOUY P, GONZALEZ M. Connecting discrete particle mechanics to continuum granular micromechanics: anisotropic continuum properties under compaction[J]. Mechanics Research Communications, 2018, 92: 1-13.

[23] NOWAK E R, KNIGHT J B, BENNAIM E, et al. Density fluctuations in vibrated granular materials[J]. Physical Review E: Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1998, 57(2): 1971-1982.

(编辑  陈灿华)

收稿日期： 2018 -10 -12; 修回日期： 2018 -12 -22

基金项目(Foundation item)：国家自然科学基金资助项目(51475475)(Project(51475475) supported by the National Natural Science Foundation of China);

通信作者：欧阳鸿武，博士，教授，从事汽车轻量化和高性能传动技术研究；E-mail：oyhw@mail.csu.edu.cn