J. Cent. South Univ. Technol. (2010) 17: 911-917

DOI: 10.1007/s11771-010-0576-3

Modeling of metadynamic recrystallization kinetics after hot deformation of low-alloy steel Q345B

MA Bo(马博)^{1, 2}, PENG Yan(彭艳)^{1, 2}, LIU Yun-fei(刘云飞)^{1, 2}, JIA Bin(贾斌)^{1, 2}

1. State Key Laboratory of Metastable Materials Science and Technology, Yanshan University,

Qinhuangdao 066004, China;

2. Engineering Research Center of Rolling Equipment and Complete Technology of Ministry of Education,

Yanshan University, Qinhuangdao 066004, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: Based on the steady-state strain measured by single-pass hot compression tests, the method by a double-pass hot compression testing was developed to measure the metadynamic-recrystallization kinetics. The metadynamic recrystallization behavior of low-alloy steel Q345B during hot compression deformation was investigated in the temperature range of 1 000-1 100 ℃, the strain rate range of 0.01-0.10 s^-1 and the interpass time range of 0.5-50 s on a Gleeble-3500 thermo-simulation machine. The results show that metadynamic recrystallization during the interpass time can be observed. As the deformation temperature and strain rate increase, softening caused by metadynamic recrystallization is obvious. According to the data of thermo-simulation, the metadynamic recrystallization activation energy is obtained to be Q_md=100.674 kJ/mol and metadynamic recrystallization kinetics model is set up. Finally, the error analysis of metadynamic recrystallization kinetics model proves that the model has high accuracy (correlation coefficient R=0.988 6).

Key words: low-alloy steel; kinetics model; hot deformation; metadynamic recrystallization; activation energy

1 Introduction

Metallic materials have a certain degree of static softening during the multi-pass rolling process as a consequence of strain accumulation between passes, e.g. metadynamic recrystallization (MDRX), static recovery (SRV) and static recrystallization (SRX). Usually, the onset of dynamic recrystallization (DRX) during hot deformation occurs when a critical strain, ε_c, is reached. This critical strain is related to the peak strain, ε_p (the strain corresponding to the maximum stress in the flow curve), following relationship of the type, ε_c =Aε_p. For different materials, values between 0.60 and 0.85 [1-4] have been reported for constant A. MDRX during the interpass time occurs by the continued growth of the nuclei formed as a result of DRX during hot deformation [5-6]. Hence, MDRX does not require an incubation time and such rapid interpass softening can affect the mechanical properties, even when the interpass time is short. Therefore, the establishment of metallic materials MDRX kinetics model is an essential part of simulating the evolution of microstructure during the multi-pass deformation [7-8].

ELWAZRI et al [9] investigated the kinetics of metadynamic recrystallization in vanadium microalloyed high carbon steels. TOLOUI and SERAJZADEH [10] developed an integrated mathematical model to predict distributions of temperature, strain and strain rate during hot rolling as well as the subsequent microstructural changes after hot deformation. As the national infrastructure investment increases and the plan for development of the west regions is carried out, market demand of medium plate is increasing. Faced with broad market demand, we a high strength low-alloy (HSLA) structural steel Q345B, developed which is a well-known variety of structural steel for mining machinery, bridges, building steel, and so on, because of its high strength and good impact toughness at low temperature [11]. FENG  et al [12] and SUN et al [13] studied the mechanical and metallurgy behaviour of steel Q345B. Despite some efforts invested into the behaviors of steel Q345B, the kinetics of metadynamic recrystallization in the hot deformed steel Q345B still needs further investigation. Therefore, the establishment of MDRX kinetics model based on the systematic MDRX research of steel Q345B by Gleeble-3500 thermo-simulation machine contributes to the development of multipass hot rolling process to control the rolling process more accurately, thereby enhancing the mechanical properties of product.

2 Experimental

2.1 Experimental materials

Specimen material is HSLA steel Q345B, and its chemical composition is shown in Table 1.

Table 1 Chemical composition of test steel (mass fraction, %)

2.2 Experimental methods

Cylindrical specimens of 10 mm in diameter and  15 mm in height were taken for the research of MDRX kinetics model. Its surface should be smooth.

MDRX during the interpass time occurs by the the nuclei formed as a result of DRX during hot deformation, while SRX occurs by the nuclei not formed as a result of DRX. In the experiment, in order to avoid the impact of SRX on MDRX and establish a more accurate MDRX kinetics model, DRX should occur about 100% softening during the first pass deformation, i.e., the true strain reaches the steady-state strain, ε_ss. Because strain rate is the primary parameter affecting MDRX kinetics, with a small effect of deformation temperature but insensitivity to strain [14-17], the true strain should be higher than or equal to the steady-state strain during the first pass in order to research MDRX evolution process. Flow curves of single-pass hot compression tests at different deformation temperatures and strain rates are shown in Fig.1. From this figure, it can be seen that, ε_ss≥0.38.

According to the results of single-pass hot compression test, double-pass hot compression tests were performed in this work. All specimens were austenitized at 1 200 ℃ for 3 min. To determine the effects of deformation temperature and strain rate, a cooling rate of 5 ℃/s was applied from initial temperature to deformation temperature (1 000-1 100 ℃). The first pass deformation was applied at a selected strain rate (0.01-0.1 s^-1) until the selected strain of 0.5 was attained. The second pass deformation was applied after specific interpass time (0.5-50 s) until the selected strain of 0.2 was attained. The deformation schedule employed for this test is displayed in Fig.2.

3 Results and analysis

3.1 Stress-strain curves

Stress-strain curves for steel Q345B deformed at

Fig.1 Flow curves of single-pass hot compression tests at different deformation conditions: (a) θ=1 100 ℃; (b) =  0.01 s^-1

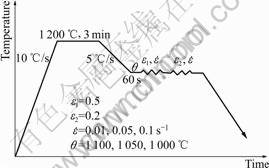
Fig.2 Schematic illustration of double-pass hot compression test

different deformation temperatures and strain rates are shown in Fig.3. Several double-pass hot compression deformation tests with increasing interpass time are plotted together to demonstrate the effect of interpass time on the flow curves. When the deformation temperature and strain rate are relatively low and the interpass time is very short, little static softening generated by MDRX takes place (see the interpass time of 0.5 and 1 s in Figs.3(a), (d) and (e)). As a consequence

Fig.3 Flow curves of two-pass hot compression tests for different interpass time under different deformation conditions: (a) θ=1 100 ℃, =0.01 s^-1; (b) θ=1 100 ℃, =0.1 s^-1; (c) θ=1 100 ℃, =0.05 s^-1; (d) θ=1 050 ℃, =0.01 s^-1; (e) θ=   1 000 ℃, = 0.01 s^-1

of the lack of softening, the second pass curve displays little further work-hardening and reaches a steady state quickly. In most cases, much static softening takes place, even when the interpass time is quite short. As a consequence of the rapid softening, the second curve displays renewed work-hardening. The second curve work hardens in a similar way to the first curve so as to rebuild the dislocation structure. Much softening taking place during the interpass time is responsible for the presence of a new DRX peak in the second curve. This peak appears at larger strains when the interpass time is increased due to the necessity of rebuilding more of the dislocation structure before DRX can be resumed.

3.2 MDRX softening measurement

There are many methods to calculate the volume fraction of MDRX [18-19]. In this work, the 0.2% offset yield strength was used to determine the softening generated by MDRX [20-23]. The volume fraction of MDRX (X_md) is measured by

                              (1)

where σ_m is the flow stress at the interruption; σ₁ is the offset stress at the first pass deformation; and σ₂ is the offset stress at the second pass deformation, as shown in Fig.4.

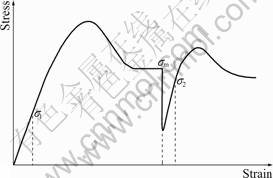
Fig.4 Schematic illustration of MDRX fraction calculation method

3.3 Effect of deformation parameters on MDRX

The effect of deformation temperature and strain rate on MDRX of investigated steel is shown in Fig.5. All the softening curves are of sigmoidal shape. It is evident that the softening curve follows the Avrami equation. The process of MDRX grain growth is fast with the increase of deformation temperature. Thus, MDRX occurs more fully. Similarly, MDRX occurs more easily as the strain rate increases. At a deformation temperature of 1 100 ℃ and a strain rate of 0.1 s^-1, the softening process is so fast that DRX occurs about 48% softening after the shortest achievable interpass time of 0.5 s. Therefore, at higher temperature or greater strain rate, the time for 50% MDRXcannot be detected in the experimental conditions.

Fig.5 Effect of deformation temperature and strain rate on MDRX

4 Modeling MDRX kinetics

The kinetics of MDRX is usually described by an Avrami equation of the following form [17, 24-28]:

                (2)

where t is the interpass time (s); and  is the time for 50% MDRX (s). Previous studies showed that  is mainly affected by the chemical composition of materials and deformation conditions. The expression most widely used for this parameter is [7-8, 21]

                      (3)

where 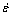 is the strain rate (s^-1); Q_md is the activation energy of MDRX (kJ/mol); R is the gas constant    (8.31 J/(mol?K)); T is the deformation temperature (K); A_md and n_md are material dependent constants.

4.1 Determination of k_md

In order to determine k_md, taking the natural logarithm on both sides of Eq.(2) yields

        (4)

Taking partial derivative of on both sides of Eq.(4) yields

                     (5)

Eq.(5) proves that ln{ln[1/(1-X_md)]} has a linear relationship with 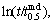 as shown in Fig.6. k_md can be obtained by least squares method, k_md=0.662 7.

Fig.6 Relationship between ln{ln[1/(1-X_md)]} and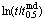

4.2 Determination of 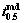 on deformation parameters

Taking the natural logarithm on both sides of Eq.(3) yields

                 (6)

4.2.1 Activation energy of MDRX

The effect of deformation temperature on  was estimated at a constant strain rate. Under this condition,  has a linear relationship with 1/T. Q_md was obtained from the slope of  as a function of    1/T plot, i.e. the slope is Q_md/R. Fig.7 shows the graph for this steel. Q_md can be obtained by least squares method, Q_md=100.674 kJ/mol.

Fig.7 Relationship between  and 1/T

4.2.2 Effect of strain rate

The effect of strain rate on  was estimated at a constant temperature. Under this condition, Eq.(6) on both sides takes partial derivative of , and there is

                               (7)

Eq.(7) proves that  has a linear relationship with , as shown in Fig.8. n_md can be obtained, n_md= -0.762 6. This accords with the values (from -0.84 to -0.60) observed by other workers [8, 15, 21].

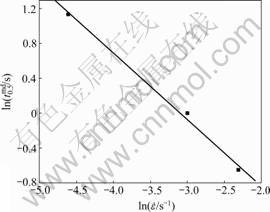
Fig.8 Relationship between  and

4.3 Mathematical model

In summary, the present data for MDRX can be reasonably represented with the following equations:

              (8)

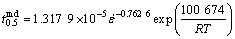        (9)

5 Comparison between calculated values and measured values

In order to verify the accuracy of MDRX kinetics model, comparison between the calculated values and measured values for the volume fraction of MDRX under different deformation conditions is shown in Fig.9. It can be seen from these figures that calculated and measured values are in good agreement (correlation coefficient R=0.988 6). Therefore, this model can give an accurate estimate of the softening behaviors and microstructural evolution for steel Q345B and contribute to the development of multipass hot rolling process to control the rolling process more accurately.

6 Conclusions

(1) Based on the steady-state strain measured by single-pass hot compression tests, double-pass hot compression test process is developed. The true stress-true strain curves indicate that three exists MDRX process of low-alloy steel Q345B. As the deformation temperature and strain rate increase, softening caused by MDRX is obvious.

(2) At a deformation temperature of 1 100 ℃ and a strain rate of 0.1 s^-1, the softening process is so fast that DRX occurs about 48% softening after the shortest achievable interpass time of 0.5 s. Therefore, at higher temperature or greater strain rate, the time for 50% MDRX () cannot be detected in the experimental conditions.

(3) According to the data of thermo-simulation, the MDRX activation energy of 100.674 kJ/mol is obtained and MDRX kinetics model is set up.

(4) The calculated and measured values for the volume fraction of MDRX under different deformation conditions are in good agreement. Therefore, this model can give an accurate estimate of the softening behaviors and microstructural evolution for steel Q345B and contribute to the development of multipass hot rolling process to control the rolling process more accurately.

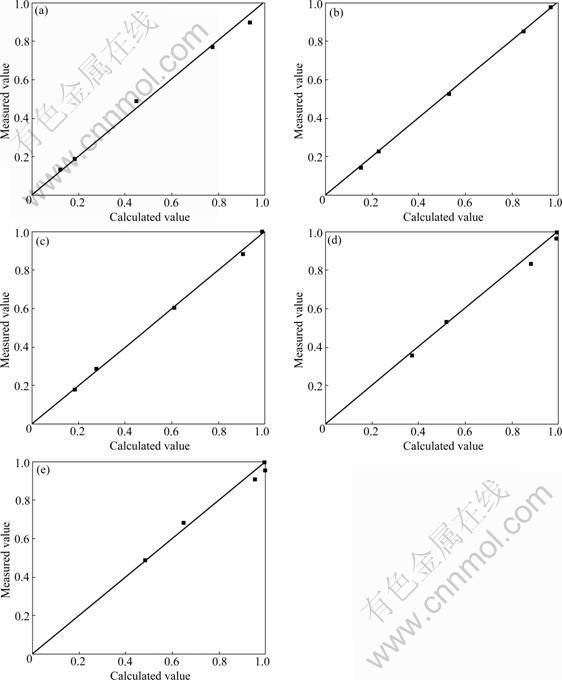
Fig.9 Comparison between calculated values and measured values for volume fraction of MDRX:  (a) θ=1 000 ℃, 0.01 s^-1; (b) θ=1 050 ℃, 0.01 s^-1; (c) θ=1 100 ℃, 0.01 s^-1; (d) θ=    1 100 ℃, 0.05 s^-1; (e) θ=1 100 ℃, 0.10 s^-1

References

[1] ZHANG Bin, ZHANG Hong-bing, RUAN Xue-yu. Dynamic recrystallization behavior of 35CrMo structural steel [J]. Journal of Central South University of Technology, 2003, 10(1): 13-19.

[2] KIM S I, CHOI S H, LEE Y. Influence of phosphorous and boron on dynamic recrystallization and microstructures of hot-rolled interstitial free steel [J]. Mater Sci Eng A, 2005, 406(1/2): 125-133.

[3] PEREDA B, FERNANDEZ A I, LOPEZ B, RODRIGUEZ-IBABE J M. Effect of Mo on dynamic recrystallization behavior of Nb-Mo microalloyed steels [J]. ISIJ International, 2007, 47(6): 860-868.

[4] DEHGHAN-MANSHADI A, BARNETT M R, HODGSON P D. Recrystallization in AISI 304 austenitic stainless steel during and after hot deformation [J]. Mater Sci Eng A, 2008, 485(1/2): 664-672.

[5] ZHOU Ji-hua, GUAN Ke-zhi. Deformation resistance of metals [M]. Beijing: China Machine Press, 1988: 13-17. (in Chinese)

[6] SERAJZADEH S. A study on kinetics of static and metadynamic recrystallization during hot rolling [J]. Mater Sci Eng A, 2007, 448(1/2): 146-153.

[7] LIN Yong-cheng, CHEN Ming-song. Study of microstructural evolution during metadynamic recrystallization in a low-alloy steel [J]. Mater Sci Eng A, 2009, 501(1/2): 229-234.

[8] CHO S H, KANG K B, JONAS J J. Mathematical modeling of the recrystallization kinetics of Nb microalloyed steel [J]. ISIJ International, 2001, 41(7): 766-773.

[9] ELWAZRI A M, ESSADIQI E, YUE S. Kinetics of metadynamic recrystallization in microalloyed hypereutectoid steels [J]. ISIJ International, 2004, 44(4): 744-752.

[10] TOLOUI M, SERAJZADEH S. Modelling recrystallization kinetics during hot rolling of AA5083 [J]. Journal of Materials Processing Technology, 2007, 184(1/2/3): 345-353.

[11] MA Bo, PENG Yan, JIA Bin, LIU Yun-fei. Static recrystallization kinetics model after hot deformation of low-alloy steel Q345B [J]. Journal of Iron and Steel Research, International, 2010, 17(8): 61-68.

[12] FENG Yun-li, CHEN Hua-hui, WANG Cheng, CHEN Li-bin. Microstructure and properties of Q345B truck frame strip produced by FTSR hot rolling technology [J]. Heat Treatment of Metals, 2006, 31(6): 25-27. (in Chinese)

[13] SUN Yan-hui, NI You-jin, XU Zhong-bo, CAI Kai-ke. Mechanical and metallurgy behaviour of medium carbon steel [J]. Journal of University of Science and Technology Beijing, 2009, 31(6): 708-713. (in Chinese)

[14] ROUCOULES C, HODGSON P D, YUE S, JONAS J J. Softening and microstructural change following the dynamic recrystallization of austenite [J]. Metall Trans A, 1994, 25(2): 389-400.

[15] ROUCOULES C, YUE S, JONAS J J. Effect of alloying elements on metadynamic recrystallization in HSLA steels [J]. Metall Trans A, 1995, 26(1): 181-190.

[16] RYAN N D, MCQUEEN H J. Dynamic softening mechanisms in 304 austenitic stainless steel [J]. Canadian Metallurgical Quarterly, 1990, 29(2): 147-162.

[17] SUN W P, HAWBOLT E B. Comparison between static and metadynamic recrystallization—An application to the hot rolling of steels [J]. ISIJ International, 1997, 37(10): 1000-1009.

[18] FERNANDEZ A I, LOPEZ B, RODRIGUEZ-IBABE J M. Relationship between the austenite recrystallization fraction and the softening measured from the interrupted torsion test technique [J]. Scripta Materialia, 1999, 40(5): 543-549.

[19] LI G, MACCAGNO T M, BAI D Q, JONAS J J. Effect of initial grain size on the static recrystallization kinetics of Nb microalloyed steels [J]. ISIJ International, 1996, 36(12): 1479-1485.

[20] YUE Chong-xiang, ZHANG Li-wen, LIAO Shu-lun, GAO Hui-ju. Mathematical models for predicting the austenite grain size in hot working of GCr15 steel [J]. Computational Materials Science, 2009, 45(2): 462-466.

[21] URANGA P, FERNANDEZ A I, LOPEZ B. Transition between static and metadynamic recrystallization kinetics in coarse Nb microalloyed austenite [J]. Mater Sci Eng A, 2003, 319(1/2): 319- 327.

[22] LIN Yong-cheng, CHEN Ming-song, ZHONG Jue. Study of metadynamic recrystallization behaviors in a low-alloy steel [J]. Journal of Materials Processing Technology, 2009, 209(5): 2477-2482.

[23] LI Xiong, ZHANG Hong-bing, RUAN Xue-yu, LUO Zhong-hua, ZHANG Yan. Kinetics for static recrystallization after hot working of 0.38C-0.99Cr-0.16Mo steel [J]. Journal of Central South University of Technology, 2004, 11(4): 353-357.

[24] ZHANG Zhao-hui, LIU Yong-ning, LIANG Xiao-kai, SHE Yuan. The effect of Nb on recrystallization behavior of a Nb micro-alloyed steel [J]. Mater Sci Eng A, 2008, 474(1/2): 254-260.

[25] JUNG K H, LEE H W, IM Y T. Numerical prediction of austenite grain size in a bar rolling process using an evolution model based on a hot compression test [J]. Mater Sci Eng A, 2009, 519(1/2): 94-104.

[26] BIANCHI J H, KARJALAINEN L P. Modelling of dynamic and metadynamic recrystallisation during bar rolling of a medium carbon spring steel [J]. Journal of Materials Processing Technology, 2005, 160(3): 267-277.

[27] CARTMILL M R, BARNETT M R, ZAHIRI S H, HODGSON P D. An analysis of the transition between strain dependent and independent softening in austenite [J]. ISIJ International, 2005, 45(12): 1903-1908.

[28] BONTCHEVA N, PETZOV G. Total simulation model of the thermo-mechanical process in shape rolling of steel rods [J]. Computational Materials Science, 2005, 34(4): 377-388.

(Edited by YANG You-ping)

Foundation item: Project(101048) supported by Fok Ying Tung Education Foundation; Project(E2008000835) supported by the Natural Science Foundation of Hebei Province, China

Received date: 2009-10-26; Accepted date: 2010-03-22

Corresponding author: PENG Yan, PhD, Professor; Tel: +86-13933691137; E-mail: pengyan@ysu.edu.cn