J. Cent. South Univ. (2016) 23: 3192-3203

DOI: 10.1007/s11771-016-3385-5

Numerical modeling dynamic process of multi-feed microwave heating of industrial solution media

YANG Biao(杨彪)^{1, 2, 3}, SUN Jun(孙俊)^{1, 2, 3}, LI Wei(李玮)^{2, 3, 4}, PENG Jin-hui(彭金辉)^{2, 3},

LI You-ling(李幼灵)⁵, LUO Hui-long(罗会龙)^{2, 3}, GUO Sheng-hui(郭胜惠)^{2, 3},

ZHANG Zhu-ming(张竹敏)⁵, SU He-zhou(苏鹤州)⁵, SHI Ya-ming(史亚鸣)⁵

1. Faculty of Information Engineering and Automation, Kunming University of Science and Technology,Kunming 650500, China;

2. Key Laboratory of Unconventional Metallurgy, Ministry of Education,

Kunming University of Science and Technology, Kunming 650093, China;

3. Engineering Laboratory of Microwave Application and Equipment Technology of Yunnan Province,

Kunming University of Science and Technology, Kunming 650093, China;

4. Faculty of Science, Kunming University of Science and Technology, Kunming 650093, China;

5. Kunming Iron & Steel Holding Co., Ltd., Kunming 650302, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: The exothermic efficiency of microwave heating an electrolyte/water solution is remarkably high due to the dielectric heating by orientation polarization of water and resistance heating by the Joule process occurred simultaneously compared with pure water. A three-dimensional finite element numerical model of multi-feed microwave heating industrial liquids continuously flowing in a meter-scale circular tube is presented. The temperature field inside the applicator tube in the cavity is solved by COMSOL Multiphysics and professional programming to describe the momentum, energy and Maxwell’s equations. The evaluations of the electromagnetic field, the temperature distribution and the velocity field are simulated for the fluids dynamically heated by single- and multi-feed microwave system, respectively. Both the pilot experimental investigations and numerical results of microwave with single-feed heating for fluids with different effective permittivity and flow rates show that the presented numerical modeling makes it possible to analyze dynamic process of multi-feed microwave heating the industrial liquid. The study aids in enhancing the understanding and optimizing of dynamic process in the use of multi-feed microwave heating industrial continuous flow for a variety of material properties and technical parameters.

Key words: microwave with multi-feed heating; industrial flow; dynamical process; numerical computation; solution media

1 Introduction

There is growing interest in the use of microwaves to process materials. The main application of microwave processing of materials is in heating. Microwave technique has become a common method to generate heat in modern industries [1]. When microwave heating an electrolyte/water solution, dielectric heating by orientation polarization of water and resistance heating by the Joule process taking place by space-charge polarization occurs simultaneously compared with pure water, and thus the exothermic efficiency becomes remarkably high [2-3]. However, some problems seriously hinder the widespread use of microwave energy. One of these problems is associated with a volumetric heat generation caused by the uneven spatial absorption of electromagnetic energy inside the heated object [4], which is a type of thermal phenomenon due to the interaction between the electromagnetic waves and materials. A number of investigations [5-8] have been documented to find the physical original of the heating process and hope that it leads to a general rule in preventing runaway. Temperature profiles of the irradiated liquid are necessary in order to achieve this. These temperature profiles give a good insight in uneven spatial absorption of energy. The process of uneven spatial absorption is a natural nonlinear problem and can be explained by taking the temperature dependence of the permittivity ε into account. Temperature profile is a function of the dielectric and thermal properties of the material, the radiation frequency, the specific power, and the geometry of the microwave heating system [9-11]. These variables make it difficult to precisely control the heating process in order to obtain the desired temperature profiles in the material. Due to the complexity of the basic physical origin of the volumetric heat generation, numerical modeling has been widely used to investigate the microwave heating process [12]. Generally, prediction of microwave energy deposition requires the solution of Maxwell’s equations, which determines the electromagnetic field in the microwave cavity. Knowledge of three-dimensional (3D) temperature profile distribution in the heated objects is critically needed to optimize the microwave heating process [13]. 3D simulations of microwave propagation and energy deposition are presented in [14-16] to determine the temperature distribution inside and at the surface of materials during batch microwave processing.

Success in the numerical simulation of electromagnetic propagation has recently generated interest in numerical modeling of heat transfer induced by microwave radiation. CLEMENS and SALTIEL [17] developed a model of microwave heating of a solid specimen. Their model accounts for effects of microwave frequency, dielectric properties of the specimen, and the size of the sample on the microwave energy deposition in a 2D formulation. RATANADECHO et al [18] were the first who investigated microwave heating of a liquid layer in a rectangular waveguide. The movement of liquid particles induced by microwave heating was taken into account. Coupled electromagnetic, hydrodynamic and thermal fields were simulated with 2D. The uneven spatial variation of the electromagnetic field was obtained by solving Maxwell’s equations with the finite difference time domain (FDTD) method, which developed by YEE [19] have been widely utilized to solve Maxwell’s equations. Their work demonstrated an algorithm for resolving the coupling of Maxwell’s, momentum, and energy equations by comparing with experimental results. Microwave heating of a liquid flowing in a rectangular duct passing through a cubic cavity, which better approximates that of real industrial system, was studied by the authors’ group [20], which were simulated temperature distributions in different liquids. The geometry is similar to that investigated in Refs. [21-22], but extended to 3D. Numerical simulations of microwave heating a liquid continuously flowing in a circular pipe are reported in Ref. [20], whose microwave operated in single-feed with 5000W at a frequency of 915 MHz. Their work accounts for the dielectric properties of liquid and the geometry of the microwave heating system, which causes the outlet temperature distribution. An algorithm is utilized to couple Maxwell’s and energy equations.

The study on the mechanism of microwave heating is complex and multidisciplinary in nature [23]. In general, prediction of microwave energy deposition to the sample requires the solution of Maxwell’s equations. A number of studies have been documented that dealt with numerical modeling of microwave heating process in a cavity. Most of the current research has focused on laboratory-scale, exploratory efforts. However, to our best knowledge, there is little information on numerical simulations of the microwave with multi-feed heating of a liquid continuously flowing in a circular pipe of the real industrial microwave heating system, which limits the further application of microwave heating in industry [24]. Work is needed to scale-up process and system designs to continuous processes. Process scaling includes model simulation, system design and integration, and an understanding of the costs and benefits involved in moving to production scale [23]. An important element of microwave process development and system design is the capability to model electromagnetic interactions. Therefore, there is an urgent need to investigate numerical modeling dynamic process of high power microwave with multi-feed heating of industrial liquid, which can be understood the variation of dielectric properties with temperature and processing state. Computer modeling can be used to optimize feed or applicator system design, establish achievable processing windows, and conduct realistic process simulations for given dielectric properties, sample size, and desired processing conditions. In this paper, a meter-scale microwave cavity with multi-feed designed to generate exactly released in the center of the applicator tube of and near the wall of energy distribution is investigated. This research is to investigate microwave heating a liquid in a 3D geometry which better approximates that of real industrial systems. The combination of the COMSOL Multiphysics and the professional programming similar to that reported in Refs. [18, 20] is used in this study to couple Maxwell’s and heat transfer equations. In order to optimize the design of the microwave heating system, the effects of radius of the applicator tube, the flow rate through the applicator tube, the location of microwave feed at a frequency of 2450 MHz are investigated.

2 Modeling and simulations

2.1 Multi physic field coupling equations

The analyzed model of continuous flow microwave heating liquids deals with the strongly-coupled electromagnetic, temperature and flow field. Generally, the numerical modeling is always described by a set of coupled equations. As for microwave field, its distributions within the resonance cavity and sample can be determined by [25]

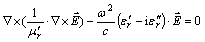            (1)

where 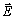denotes the strength of microwaves’ electric field; and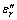 are the real and the imaginary components of the complex relative permittivity of the liquid, respectively; at the operating frequency f (in 2.45 GHz), ω=2πf is the angular frequency; is the complex operator; is the relative permeability; c is the velocity of electromagnetic wave in free space (3×10⁸ m·s^-1). Once the electric field intensity distribution in the cavity is solved by applying Eq. (1), the volumetric energy generation due to the absorption for the microwave power is [26]

                       (2)

where σ is the electrical conductivity (S·m^-1); ε₀ is the permittivity in vacuum (1/(36π)×10^-9 F·m^-1). The first term in Eq. (2) expresses conduction loss heating; the second term denotes dielectric loss heating.

Once heat generation has been formulated, the temperature distribution is given by the heat conduction equation:

                   (3)

where ρ, c_p, k, T, , t and Q stand for density (kg·m^-3), specific heat capacity (J·kg^-1·K^-1), thermal conductivity (W·K^-1·m^-1), temperature (K), velocity vector (m·s^-1),time (s) and volumetric heat generation (W·m^-3), respectively.

As for the velocity field, the velocity distribution is determined by the solution of the following Navier- Stokes equations:

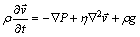                      (4)

                                    (5)

where P is the pressure (N·m^-2); g is the gravitational acceleration (m·s^-2); η is the apparent viscosity of the non-Newtonian fluid (Pa·s), which is assumed to obey the power-law [20].

2.2 Numerical solution process of model with single-feed

A 3D single-feed microwave heating the liquid model has been developed using the COMSOL Multiphysics v4.3 software. Figure 1 shows the schematic diagram of the single-feed microwave system examined in the research. The model consists of the cavity (44 mm in radius and 64.8 mm in height), the BJ-26 waveguide, and a vertically positioned applicator tube (5 mm in radius and 100 mm in height) that passes through the cavity. The excitation port of the waveguide is powered by 0.5 kW at a frequency of 2.45 GHz in the fundamental mode TM₀₁₀. The liquid flows through the applicator tube in the upward direction, absorbing the microwave energy as it passes through the tube. The microwave is transmitted through the waveguide towards the applicator tube located in the center of the resonant cavity. It is assumed that no-slip and loss heat occurs at the inner surface of the applicator tube during the heating process.

Fig. 1 Model of single-feed microwave heating liquids

The cavity and waveguide port are filled with air whose ε_r=μ_r=1; and the liquids has thermal conductivity k=0.6037 W·K^-1·m^-1, density ρ=0.9957 kg·m^-3, specific heat coefficient c_p=4176.6 J·kg^-1·K^-1, electrical conductivity σ=10^-5 S·m^-1, the relative dielectric constant the relative loss factor viscosity μ=0.001 Pa·s, and the initial temperature T= 20 °C. It is assumed that no phase change occurs, and the physical properties have been considered independent with temperature during the heating process.

The coupled non-linear set of Eqs. (1)-(5) is solved numerically by using COMSOL Multiphysics and professional programming. The entire numerical solution procedure is an iterative computation until the convergence criterion of the computational process is reached. For the numerical accuracy and computational convergence, a balanced combination of the computer resource consumption and a grid of moderate size are required. The maximum cell size of a grid in the waveguide and cavity, and in the applicator tube is 4.5 mm, and 1.2 mm, respectively.

The computational process is to first compute the distribution of the microwave field by using the GMRES solver to solve the wave equation of RF module. The volumetric heat generation depending on feed microwave is computed by solving energy balance equation by using the heat transport module. Once heat generation has been obtained, the temperature distribution is solved by using PARDISO solver. The Navier-Stokes equation is solved by using the hydrodynamic module. The velocity distribution of the liquid is computed by using PARDISO solver. The heat transport module and the hydrodynamic module are coupled to the velocity field. In this work, the dynamic process is simulated to show the change of temperature within applicator tube with time, the effects of flow velocity (0.01, 0.02, 0.04 m·s^-1) and loss factor (0.5, 1, 1.5) on the mean temperature within applicator tube. The simulation researches on single-feed microwave above are implemented on an AMD Core^TM 4 CPU running at 2.8 GHz 8 GB memory 64 bit Ubuntu Linux OS.

2.3 Results and discussion on model with single-feed

To verify the rationality of the model, the spatial distribution of the electric field was calculated for the case of the empty cavity (which corresponds to that of air) and for the case when the liquid flows through the applicator tube in the cavity, as shown in Fig. 2, respectively. As expected, Fig. 2(a) shows the maximum field intensity (which is E_max=33 kV/m) near the center of the applicator tube. Apparently, positioning the heated products at the centre of applicator tube in the microwave cavity thus provides the best heating effect.

Fig. 2 Electric fields distribution in empty cavity (a) and cavity flowing liquids (b)

But instead, electric field distribution in the empty cavity will be affected and turned the operating mode of the resonant cavity into change after the introduction of the liquid. In order to keep the operating mode of the resonant cavity unchanged, and the maximum electric field was still located at the center of the applicator tube when the fluid flows into the cavity, we should select the thin applicator tube with the radius of 5 mm, and the dielectric constant of the fluid as ε′=5. From Fig. 2(b), it is evident that the electric field distribution in the cavity is changed very little when the fluid flows into the thin tube in the cavity, but kept the operating mode of the resonant cavity unchanged, and the maximum field strength which is approximately that of the empty cavity (which is E_max=33 kV/m) is still located at the center of the resonant cavity. Therefore, the cavity model for the dynamic process simulation of microwave heating fluid is reasonable.

The spatial distribution of the temperature for the liquids at a flow rate of 0.02 m/s is presented in Fig. 3. Results are shown in the vertical x-z plane (y=0), and the horizontal x-y plane at three different cross sectional (which are z=20, 40, 55 mm) location, respectively. The evidence that the temperature increases in the direction as the liquid particle enters the applicator tube, which is heated by microwave radiation (of course, t=0 s, temperature equals to initial value, 20 °C because of liquid not being radiated by microwave in Fig. 3(a)), in the z-direction is seen in Figs. 3(b), 3(c), and 3(d). Figures 3(c) and (d) reveal different cross-sectional temperature distributions of the fluid in applicator tube at t=1 s and 2 s, respectively. From Figs. 3(c) and (d), it is observed that the more uniform distribution is the case of t=1 s, whereas the case of t=2 s shows a very high temperature region/hot spot near the wall of tube. For the case of t=1 s, the contour values of the cross-section temperature range from 25 °C to 28 °C at the middle of the tube (z=40 mm), whereas for the case of t=2 s these values are from 20 to 34 °C. The hot spot temperatures, for the case of t=2 s at the middle tube (z=40 mm), are from 25 °C to 34 °C; the values of the temperature as well as the area of hot spot increase (26-36 °C) at the exit of the tube (z=55 mm), where the cross-sectional contour values at the exit (z=55 mm) show very non-uniform temperature. This is because the electromagnetic power determines the temperature distribution in the x-y plane. As expected, Fig. 2 shows a well-defined peak of electromagnetic power intensity near the center of the applicator tube; although most of the microwave energy is released near the center of the tube, the reduced velocity near the wall results in higher temperature in the region near the wall. The high velocity in the core region reduces the effect of the peak of the electromagnetic power intensity on the temperature of the corresponding hot spot in the liquids, while the reduced velocity near the wall results in higher temperature in the region near the wall.

Fig. 3 Temperature distribution varying with heating time in applicator tube:

Figure 4(a) shows the mean temperature change at the outlet (z=55 mm) as the flow rate increases from 0.01 m/s to 0.04 m/s. The maximum temperature in the cross-section of the tube reaches approximately 54 °C after about 20 s at a flow rate of v=0.01 m/s, approximately 37 °C after about 10 s at a flow rate of v=0.02 m/s, and approximately 28 °C after about 5 s at a flow rate of v=0.04 m/s. It is evident that as same power was provided at all three flow rate, the higher the flow rate, the lower the mean temperature increase at the outlet is. Thus, in order to control the heated temperature, one should adjust the flow rate of the liquid. To illustrate the effect of dielectric properties on heating process, the relation between the mean temperature at outlet of the liquid and the relative loss factor at v=0.02 m/s is seen in Fig. 4(b). It is evident that with increasing loss factor of the liquid, the microwave energy absorbed by the liquid increases, and the larger loss factor results in higher mean heating temperature. Therefore, the heating rate can be adjusted by changing the dielectric loss of the heated liquid.

3 Numerical solution model with multi-feed

3.1 S parameters calculation

This section discusses S parameters calculation using the microwave source with multi-feed heating. At present, the general problem on energy researches is mainly focused on how the power carried by the electromagnetic waves can be used to transmit into the heated materials efficiently. S parameters, which are just the network ones based on the relation between the incident wave and the reflected wave, are appropriate to analyze the energy utilization efficiency of the microwave heating system. In order to optimize the design of the multi-feed microwaves system, the exciting process of the microwave cavity with two feed is simulated, also the effects of the microwave frequency, the size of material on S parameters are investigated.

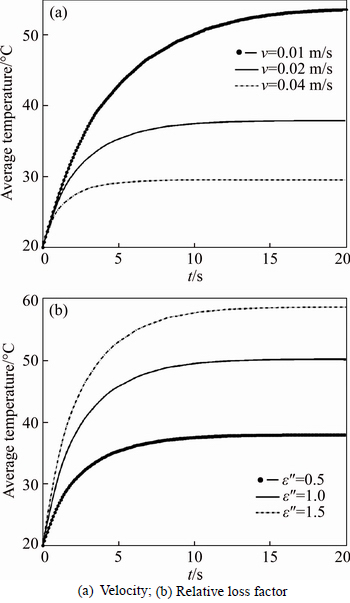
Fig. 4 Influences on mean temperature in tube:

In the following, the two feed microwave cavity will be described. Its dimensions are 24 cm×20 cm×26 cm. A cubic load is placed in the center of the cavity. The length of the load is 5 cm and the complex permittivity of the load is . The two feed are located at the center position of half plane of the right broad side of the cavity, through these two feed the microwaves with input power of 1000 W operating in TE₁₀ mode are transmitted into the cavity. The transverse dimension of the feed is 8.636 cm×4.318 cm, and its length is 5 cm. The variation of S parameters with exciting frequency, which is the range of (2450±50) MHz, is given in Fig. 5. It can be seen that for linear, symmetric microwave feed network, a relation is found as S₁₁=S₂₂, S₂₁=S₁₂. Therefore, in the numerical computations, the optimal conditions of utilizing microwave energy in certain domain can be determined through calculating the minimum value of the expression,For example, the microwave power feed operates at 2500 MHz, does reach its minimum, which is equal to 0.264. Under this condition, the reflected wave and penetrated wave of the microwave cavity with two feed are minimum, and the microwave energy of around 73% is absorbed by the load.

Fig. 5 Variation of S parameters with exciting frequency

When microwave frequency is 2450 MHz, the length of the cubic load l increases at step of 10 mm within the load length range from 10 mm to 100 mm, as illustrated by Fig. 6. It can be seen from Fig. 6 that ceteris paribus, there exists a length of the cubic load, which makes the reflected microwave energy minimum, and the energy absorption efficiency of the load is maximum. The results can be obtained that at l=100 reach minimum though the calculation. Its minimum value is 0.276, which means that the microwave energy of around 73% is dissipated in the cubic load. A general conclusion is drawn that, in a multi-feed microwave heating system, to reduce the coupled energy among the microwave feed in a certain extent, the size of heated load should be increased.

Fig. 6 Variation of S parameters with length of cubic load

It is well known that optimization design is an important challenge in multi-feed microwave heating system [20], whose microwave energy utilization efficiency is related to the cavity dimension, microwave frequency, power level, feed position, and load size. In this work, the feed are positioned the six faces of heptagonal cavity (one face has the door) symmetrically, and some parameters, including the initial temperature of the heated liquid, microwave power, flow rate of liquid, and the radius of applicator tube, are also changed to study the effects on the temperature distribution and dynamic heating process.

3.2 Numerical modelling dynamic process of high- power with multi-feed microwave heating of industrial liquid

Figure 7 shows the geometrical model and its parameters of the numerical analysis in this research. The system composition is similar to that of numerical solution process of model with single-feed. Geometry parameters of characterizing system are listed in Table 1 and Table 2 lists the thermophysical and electromagnetic parameters utilized in computations and other pertinent system parameters.

Fig. 7 Geometrical parameters (a) and model (b)

Table 1 Geometry parameters of model

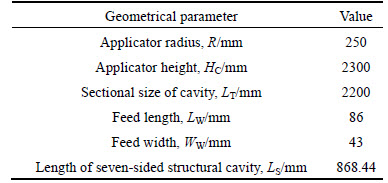
Table 2 Thermophysical, electromagnetic parameters utilized in computations

4 Results and discussion on model with multi- feed

Here, the mixed acid solution is considered, specifically, nitric acid (under 4% mass fraction of HNO₃) and hydrofluoric acid (under 0.8% mass fraction of HF). The problem of microwave heating is directly related to electromagnetic fields, the temperature distribution within a dielectric material. Therefore, knowing the dielectric properties is essential for a whole process. 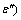The temperature-dependent data for dielectric properties (dielectric constant, and loss factor, for the mixed acid solution are plotted versus temperature in Fig. 8. In order to compare the results obtained for technical parameters, the base case is first defined. The base case is characterized by the following technical parameters: initial temperature as 40 °C, the mean flow rate as 0.1 m/s, microwave power level as 210×1.5 kW, and the applicator tube radius as 250 mm.

Fig. 8 Dielectric properties at different temperature used in calculations (ε′-dielectric constant; ε″-loss factor)

4.1 Electric field intensity distribution

An accurate evaluation of the electromagnetic fields, which determines microwave power dissipation within the dielectric materials, is very important and crucial for the whole microwave heating process. Figure 9 shows the simulated electric fields in the x-y plane (z=1150 mm) and in the y-z plane (center axis x=1100 mm).

Figure 9 shows that the space between the resonant cavity and the applicator tube is empty which corresponds to that of air and the inside applicator tube which the mixed acid flows through in the upward direction. Since the incident wave, which is transmitted through the waveguide towards the applicator tube located in the center of the resonant cavity, passing through the outside wall of the applicator tube having low permittivity is directly irradiated with the mixed acid (inside the applicator tube) having high permittivity, a major part of incident wave is reflected from the surface of the mixed acid and a stronger standing wave with a larger amplitude forms in the resonant cavity forward to the inside wall of the applicator tube while the electric field within mixed acid extinguished.

4.2 Dynamic heating process and temperature distribution

The microwave power dissipation represents the microwave power absorbed, which is eventually converted into thermal energy of the local electromagnetic heat generation in the materials. At the same time, the dielectric properties will affect the microwave energy dissipation, thus affect the variation of the temperature distribution. The system geometry corresponding to the base case is investigated. Figure 10 not only shows different temperature gains, but also exhibits different cross-sectional temperature profiles. As the fluid particle enters the applicator tube, it is heated by the microwave radiation. From Fig. 10, it is evident that the greatest temperature in the side wall of the mixed acid with the temperature decreasing towards the center of the applicator tube. This temperature is closest to the incoming microwave. This region heats up to a higher level at a faster rate than elsewhere within the liquid. However, the temperature decreases gradually along the propagation direction owing to the skin-depth heating effect and a faster flow rate in the core region. This is because, for the same wave length of a microwave, larger loss tangent and larger power absorption correspond to smaller skin-depth. From Fig. 8, it is evident that the mixed acid has a high loss tangent which causes to absorb more microwave power. Also, the velocity profile for mixed acid is sharper and the magnitude of the velocity in the region near the wall is smaller. The low flow rate in the applicator wall region increases the effect of the peak of microwave power intensity on the temperature of the corresponding hot spot in mixed acid. Figure 11 shows the distributions of the mean temperature with time in the horizontal x-y plane along with the vertical axis (z=0, 575, 1150, 1725, 2300 mm, respectively) at the applicator tube. As the temperature increases in the z-direction, dielectric properties of the mixed acid change in accordance with Fig. 8. It is observed that a very high temperature region/hot spot near the applicator wall. The contour values of the cross-section temperature ranged from 40 °C to 46 °C at the inlet of the wall of the tube (z=575 mm). The hot spot temperatures are 50.6 °C; the values of the temperature as well as the area of hot spot increase (40-50 °C) at the outlet of the tube (z=2300 mm). The cross-sectional contour values at the outlet (z=2300 mm) again show very non-uniform temperature (40-48 °C).

Fig. 9 Microwave electric field intensity distribution (V/m) in x-y plane (z=1150 mm) and in y-z plane (center axis x=1100 mm)

In the pilot experimental study of a mixed acid solution continuously flowing in a circular applicator that is subjected to the multi-feed microwave heating, the power absorbed by the acid solution is calculated based on the inlet and outlet mean temperature and physical properties of the material at room temperature using the calorimetric equation:[27]. Figure 12 shows the comparison of the outlet temperature of the mixed acid solution between the measured and numerical results at different initial temperature. It is evident that the agreement between two rising temperatures is almost the same; only the distributions of temperature of the former is slightly lower than those of the latter. This is mainly due to the heat loss when the acid solution is heated by microwave energy; and the maximum relative error of numerical computation is about 11.3%. At the initial temperature with 18 °C, the experimental and numerical results of the mixed acid solution continuously flowing heated by the multi-feed microwave system are shown in Fig. 13. It is evident that at the early stage of heating, the relative error of the numerical computation is small, and this value increases with the continuing to heat, which the maximum is about 13.1%. The large relative error is observed because of several factors including heat loss from the heated solution to the cooler surrounding air and cumulative error of numerical computation. Within the temperature range of 18-70 °C, the relative error is less than 13.1% if the numerical model is used to calculate the electromagnetic fields and temperature distribution within the material. This is acceptable for general analysis.

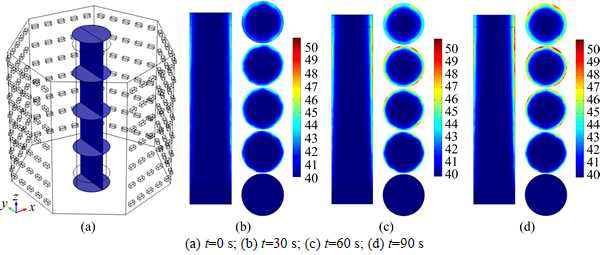
Fig. 10 Temperature distributions (°C) at horizontal x-y plane along vertical axis (z=0, 575, 1150, 1725, 2300, respectively) in applicator tube:

Fig. 11 Temperature distributions with time

Fig. 12 Variation of outlet temperature of acid solution

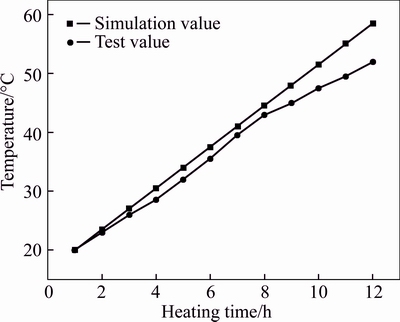
Fig. 13 Comparison of heating curves of experimental and numerical results

4.3 Effect of flow rate

This section discusses the effect of the velocity of the solution flowing continuously through the applicator tube in upward direction. Five different flow rates of the mixed acid are investigated. Figure 14 shows the velocity fields within the mixed acid for the flow rate of 0.1 m/s at various times. And Fig. 15 shows the mean temperature for mixed acid solution increase (△T) plotted versus the velocity, which corresponds to those of initial temperature with 40 °C, heating time of 90 s and different flow rates. It can be seen that the temperature gained (△T) by decreased as the flow rate increases from 0.05 m/s, 0.075 m/s, 0.1 m/s, 0.15 m/s, to 0.175 m/s (Fig. 15). As same power was provided at all flow rates, the higher the flow rate, the lower the temperature gain is. The power absorbed by the mixed acid solution was calculated based on inlet and outlet mean temperature and physical properties of the material at room temperature using the calorimetric equation [27].Additionally, the near applicator wall has a lower velocity, thus, as referred to Fig. 10, the corresponding mean temperature increase becomes bigger.

Fig. 14 Flow rate distributions (m/s) in cavity during microwave heating process:

Fig. 15 Mean temperature increase for microwave heating acid solution at different flow rates

The relationship between temperature and distance from the inlet of resonant cavity is defined by a sigmoid shaped curve. The rate of temperature increase is low initially, followed by higher rate in the middle of the applicator tube, and then again lower rate at the outlet. The increased temperature in the middle section of the applicator tube is due to higher energy density at this location corresponding to the incident microwave introduction from the waveguides into cavity. Flattening of the sigmoid shaped temperature increase curve with flow rate is a direct effect of time spent by the mixed acid in the microwave field at higher flow rates.

The rate of temperature increase observed is low in 3 s initially, at the locations of tube (z=0.525 m, corresponding to 25% tube length, at flow rate of v=0.175 m/s) followed 16 s, the mean temperature decrease is clearly observed, and then again temperature increases. This phenomenon results in the sigmoid shaped temperature profiles. Temperature decrease at the outlet is a result of low electric field intensity in this region and heat conduction and convection to the surrounding acid solution of lower temperature.

4.4 Effect of applicator radius

The effect of the radius of the applicator tube is investigated. Figure 16 shows the mean temperature increase at the outlet by choosing the radius tubes to be 100, 150, 200, 250 and 300 mm, respectively.

The inlet mean velocity is the same for all cases (v_mean=0.1 m/s). From Fig. 16, it is evident that in acid solution the temperature gained (△T) decrease as the radius of the applicator is increased. This is because increasing the radius enlarges the effective surface area for microwave penetration into the mixed acid solution. However, as the applicator radius is further increased from 200 mm, the temperature gained decreases. This phenomenon is interpreted using the concept of the cut-off frequency, which is defined as

                                    (6)

Microwaves cannot propagate into the waveguide when the frequency is below the cut-off frequency because they cannot propagate between guiding surfaces separated by less than one half of the wavelength. The effective surface area, therefore, for microwave penetration into the acid solution is reduced because microwaves cannot get a part of the applicator surface which is too close to the walls of the resonant cavity, and the energy generation in the acid solution decreases accordingly [16]. In this work, l/2=61.5 mm, the cut-off distance, however, is actually smaller than 61.5 mm since the acid solution in the applicator is not a perfectly conducting material and a portion of the microwave energy can therefore penetrate through the applicator. Comparing the mean temperature rise, it is evident that the critical radius, which is defined as the radius of the applicator above which the temperature gained decreases with the increase of the applicator radius, is approximately 170 mm. This is attributed to the effect of acid solution dielectric properties. Figure 16 shows that the mean temperature increase at the outlet does not necessarily exhibit the same trend as the power absorption. For example, although the heating time increases when the radius is increased from 200 to 300 mm, the corresponding mean temperature increase becomes smaller. Recalling that the inlet mean flow rate is the same for all applicator radiuses, the mass flow rate is smaller for the applicator with a smaller radius. Since the increase of the power absorption in the applicator with a radius of 200 mm is not significant, which is interpreted by a higher resonant in the cavity with the 150 mm radius applicator, the temperature increase in the applicator with a smaller radius (150 mm) is larger. Thus, in order to obtain the maximum temperature increase, we should select the applicator with the radius of 150 mm.

Fig. 16 Mean temperature increase at outlet: Effect of applicator radius

5 Conclusions

1) An industrial liquid continuously flowing in a meter-scale applicator tube that is subjected to multi-feed microwave heating is investigated by using COMSOL Multiphysics v4.3 and professional programming.

2) By establishing a three-dimensional numerical model for microwave heating liquid, the strongly- coupled temperature, microwave and velocity field are solved. This model of heating process by single- and multi-feed microwave system is simulated dynamically. The effects of effective permittivity of liquid, the flow rate, and the radius of the applicator tube on the temperature distribution are investigated. The electromagnetic properties determinate the dissipated microwave power in the liquid; the heating rate and temperature can be controlled by adjusting the flow rate and dielectric loss of the liquid.

3) Within the pickling temperature range, the relative error is less than 13.1%, and the values of the outlet temperature calculated by numerical model are in agreement with those actually measured in the pilot experiment for the multi-feed microwave heating meter-scale applicator tube. The geometry and dimensional size of microwave heating system also play an important role in the power absorption and distribution. Enlarging the radius of the applicator increases the effective surface available to absorb the microwave energy. However, beyond the critical radius of the applicator, it usually decreases the power absorption in the liquid.

4) This numerical model could be used both to optimize the industrial microwave applicator design processes and to determinate the relatively affecting parameters for industry.

References

[1] WEI W, YIN H M, TANG J. An optimal control problem for microwave heating [J]. Nonlinear Analysis, 2012, 75(12): 2024-2036.

[2] HORIKOSHI S, SUMI T, SERPONE N. Unusual effect of magnetic field component of the microwave radiation on aqueous electrolyte solutions [J]. Journal of Microwave Power & Electromagnetic Energy, 2012, 46(4): 215-228.

[3] YANG Biao, PENG Jin-hui, GUO Sheng-hui, ZHANG Shi-min, LI Wei, HE Tao. Acid pickling plates and strips speed control system by microwave heating based on self-adaptive fuzzy PID algorithm [J]. Journal of Central South University, 2012, 19(8): 2179-2186.

[4] VRIEZINGA C A. Thermal profiles and thermal runaway in microwave heated slabs [J]. Journal of Applied Physics, 1999, 85(7): 3774-3781.

[5] ROUSSY G, MERCIER J. Temperature runaway of microwave heated materials: study and control [J]. Journal of Microwave Power, 1985, 20(1): 47-51.

[6] CLARK D E, SUTTON W H. Microwave processing of materials [J]. Annual Review of Materials Science, 1996, 26(1): 299-331.

[7] WU X, THOMAS J R. Control of thermal runaway in microwave resonant cavities [J]. Journal of Applied Physics, 2002, 92(6): 3374-3381.

[8] SANTOS T, VALENTA M A, MONTEIRO J, SOUSA J, COSTA L C. Electromagnetic and thermal history during microwave heating [J]. Applied Thermal Engineering, 2011, 31(16): 3255-3261.

[9] GERBO N M, BOLDOR D, SABLIOV C M. Design of a measurement system for temperature distribution in continuous-flow microwave heating of pumpable fluids using infrared imaging and fiber optic technology [J]. Journal of Microwave Power and Electromagnetic Energy, 2008, 42(1): 55-65.

[10] SABLIOV C M, SANDEEP K P, SIMUNOVIC J. High frequency electromagnetism coupled with conductive heat transfer – A method to predict temperature profiles in materials heated in a focused microwave system [C]// The 4th World Congress on Microwave and Radio Frequency Applications. Austin, Texas, USA, 2004: 469-476.

[11] HU X, MALLIKARJUNAN K. Mathematical modeling of heat transfer of microwave heated fish gel [C]// ASAE Annual International Meeting. Chicago, 2002: 28-31.

[12] ZHANG Q, JACKSON T H, UNGAN A. Numerical modeling of microwave induced natural convection [J]. International Journal of Heat and Mass Transfer, 2000, 43(99): 2141-2154.

[13] KNOERZER K, REGIER M, SCHUBERT H. Measuring temperature distributions during microwave processing [M]// The Microwave Processing of Foods. USA: CPC Press, 2005: 243-263.

[14] LIU F, TURNER I, BIAKOWSKI M. A finite-difference time- domain simulation of power density distribution in a dielectric loaded microwave cavity [J]. Journal of Microwave Power and Electromagnetic Energy, 1994, 29(3): 138-147.

[15] ZHAO H, TURNER I W. An analysis of the finite-difference time-domain method for modeling the microwave heating of dielectric materials within a three-dimensional cavity system [J]. Journal of Microwave Power and Electromagnetic Energy, 1996, 31(4): 199-214.

[16] ZHANG H, TAUB A K, DOONA I A. Electromagnetics, heat transfer and thermokinetics in microwave sterilization [J]. AIChE Journal, 2001, 47(9): 1957-1968.

[17] CLEMENS J, SALTIEL C. Numerical modeling of materials processing in microwave furnaces [J]. International Journal of Heat and Mass Transfer, 1996, 39(95): 1665-1675.

[18] RATANADECHO P, AOKI K, AKAHORI M. A numerical and experimental investigation of the modeling of microwave heating for liquid layers using a rectangular waveguide (effects of natural convection and dielectric properties) [J]. Applied Mathematical Modeling, 2002, 26(3): 449-472.

[19] YEE K S. Numerical solution of initial boundary value problem involving Maxwell’s equations in isotropic media [J]. Antennas & Propagation IEEE Transactions on, 1966, 14(3): 302-307.

[20] ZHU J, KUZNETSOV A V, SANDEEP K P. Numerical simulation of forced convection in a duct subjected to microwave heating [J]. Heat and Mass Transfer, 2007, 43(3): 255-264.

[21] GASAK T, AYAPPA K G. Role of length scales on microwave thawing dynamics in 2D cylinders [J]. International Journal of Heat and Mass Transfer, 2002, 45(23): 4543-4559.

[22] AYAPPA K G, DAVIS H T, BARRINGER S A, DAVIS E A. Resonant microwave power absorption in slab and cylinders [J]. Aiche Journal, 1997, 43(3): 615-624.

[23] NATIONAL RESEARCH COUNCIL (NRC). Microwave processing of materials [M]. USA: National Materials Advisory Board, Commission on Engineering and Technical Systems, National Academy Press, 1994: 9-21.

[24] KITCHEN H J, VALLANCE S R, KENNEDY J L, TAPIA-RUIZ N, CARRASSITI L, HARRISON A, WHITTAKER A G, DRYSDALE T D, KINGMAN S W, GREGORY D H. Modern microwave methods in solid-state inorganic materials chemistry: From fundamentals to manufacturing [J]. Chemical Reviews, 2014, 114(2): 1170-1206.

[25] KONG J O. Electromagnetic wave theory [M]. Beijing: Publishing House of Electronics Industry, 2003: 328-396. (in Chinese)

[26] RISMAN P O, CELUCH-MARCYSIAK M. Electromagnetic modelling for microwave heating applications [C]// 13th International Conference on Microwaves, Radar and Wireless Communications, (MIKON-2000). Wroclaw, Poland, 2000: 167-182.

[27] LENTZ R R. Microwave heating of saline solutions [J]. Journal of Microwave Power, 1980, 15(2): 107-112.

(Edited by YANG Bing)

Foundation item: Project(KKSY201503006) supported by Scientific Research Foundation of Kunming University of Science and Technology, China; Project(2014FD009) supported by the Applied Basic Research Foundation (Youth Program) of China; Project(51090385) supported by the National Natural Science Foundation of China

Received date: 2015-11-27; Accepted date: 2016-07-11

Corresponding author: PENG Jin-hui, Professor, PhD; Tel: +86-871-5192076; Fax: +86-871-5191046; E-mail: Jhpeng_ok@Yeah.net