J. Cent. South Univ. (2012) 19: 1109-1115

DOI: 10.1007/s11771-012-1116-0

Surface-borehole electric potential survey in layered media and

its applications

SU Ben-yu(苏本玉)¹, Y. FUJIMITSU², SONG Jian-yong(宋建勇)³

1. Department of Earth Resources Engineering, Graduate School of Engineering, Kyushu University,744 Motooka, Nishi-ku, Fukuoka, 819-0395, Japan;

2. Department of Earth Resources Engineering, Faculty of Engineering, Kyushu University, 744 Motooka,Nishi-ku, Fukuoka, 819-0395, Japan;

3. Research Institute of Petroleum Exploration and Development, Petorchina, Beijing 100083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: The method in which a source is set on the surface and electric potential is received in the borehole is called surface-borehole electric potential technique. Technique of surface-borehole electric potential was employed to study electric response of layered formation. The electric potential was obtained by solving Poisson equation with finite difference method. In the course of calculation, forward modeling with finite difference method was realized by adopting bandwidth non-zero storage technique and the incomplete Cholesky conjugate gradient method. The results show that method of surface-borehole can acquire anomalous electric potential corresponding to geo-electric layers. In addition, application of appropriate mathematical operator can improve the resolution. Moreover, overburden low resistivity layers have severe influence on measuring results of surface-borehole electric potential. However, bottom low resistivity layers play a positive role in the measurement.

Key words: surface-borehole electric potential; finite difference method; forward modeling; layered media

1 Introduction

Electrical methods have been applied widely in petroleum exploration. The technology of electrical well logging is one of the indispensable tools in petroleum exploration and production. However, its measurement range is narrow and limited around the well. Even if adopting the advanced technology of array induction logging, the radius of investigation is valid only within  3 m. The technique of borehole-to-surface electric potential is also used in exploration field. SILL and WARDS [1] analyzed the geothermal range by monitoring the surface potential. STIERMAN [2] used this method to detect the contaminated groundwater which was surrounded by a waste disposal site. USHIJIMA et al [3] achieved a favorable outcome in keeping track of forward direction of high temperature superheated steam that was available for producing heavy oil. DEY and MORRISON [4] developed a compatible algorithm to simulate 3-D electric potential distribution for arbitrary shape with finite difference method. By introducing an iterative algorithm of incomplete Cholesky-conjugate gradient and a technique of bandwidth non-zero matrix storage, WU and XU [5] successfully realized fast computation of electric field forward modeling with the finite difference method by microcomputer. WANG et al proved the possibility of determining distribution range of oil reservoir using technique of borehole-to-surface electric potential by physical modeling experiment method [6] and numerical simulation method [7]. GUO et al [8] did the research on electrical responses of layered media using technique of surface-borehole electric potential. Moreover, BGP company also did a large number of studies [9-10] on 3-D borehole-surface electromagnetism (EM) modeling both in time-domain and frequency-domain. Compared with the borehole-surface electric potential, cross-well electric potential is a relatively new technique. PARASNIS [11] adopted this method to plot the continuity of conductive earth materials. SHEN et al gained the success through a lot of research on 2.5-D cross-well EM by using either forward modeling [12] or inverse modeling [13]. LI et al [14] has accomplished the calculation of all-time apparent resistivity of large loop transient electro-magnetic method with very fast simulated annealing. According to the theory and fieldwork [15], it has already been proved that cross-well EM method has a huge potential not only for studying the connection of sand body, but also for supervising the condition of drowning and locating distributions of residue oil at oilfield. In addition, HE [16] also applied the cross-well electric method in oil production in Daqing oilfield.

However, until now few people do the research about technique of the surface-borehole electric potential. Compared with measuring on the surface, the signals of measurement in the borehole are intensive, with high resolution and little noise. Moreover, the method of surface-borehole electric potential is more adaptable and much easier to operate.

The purpose of this work is to explore the feasibility and validity of applying surface-borehole method, and based on that to acquire the resolution and radius of the measurement of surface-borehole electric potential. In the numerical simulation, the resistivity of porous rock is computed by Archie formula under the assumption that the pore of rock is full of formation water with resistivity.

2 Relationship between reservoir rocks and Archie formula

The conductivity of reservoir rock is assumed to satisfy Archie formula [17]. On the other hand, for the simulation that is not fit for Archie formula, a kind of non-linear relation of conductivity [18] needs to be built up, such as the application of Hanai-Bruggman conductivity model (H-B model) [19], and porosity percolation threshold theory (PPTT) [20]. Specifically,  ρ₀ in Archie formula is supposed to symbolize the resistivity of sandstone which contains 100% pure water. As mentioned previously, ρ_w stands for formation water resistivity, and formation porosity is described as φ. The relationship among ρ₀, ρ_w and φ is defined as ρ₀=aρ_wf^-m, where m serves as the index of pore structure and a is a coefficient. It is known that the Archie formula is based on the pure sandstone with high porosity and high permeability. As presumed in the Archie formula, for the pure sandstone (without clay) filled with water (water saturation S_w=100%), the resistivities of formation and pore-water are proportional, and the coefficient of proportionality is labeled for formation index that can be calculated as below: F= ρ₀/ρ_w=1.0/φ^m. According to the information gathered from the rock sample in the Gulf of Mexico, ARCHIE [17] believed that the mathematical values of m should vary from 1.3 to 2.0. Furthermore, under the condition of pure unconsolidated sandstone, the value of m approximates to 1.3. If the condition changes to consolidated sandstone, the values of m will range from 1.8 to 2.0. When the matrix is conductive, H-B model and PPTT method can be taken into account as a useful way. In the following discussion, two fundamental postulates, which state that the formation cementation factor n is 2.0 and meanwhile Archie formula is valid, are applied.

3 Methodology

As for the subsurface 3-D media, distributions of 3-D electric potential caused by point source of current fulfill the Poisson equation [4]:

(1)

where σ(x, y, z) represents electrical conductivity of media; φ(x, y, z) is defined as electric potential; I stands for point source of current and δ means Dirac delta function. In this work, the volume discretization method is available to discretize a lower half-space of infinite area, as shown in Fig. 1. σ(i, j, k) represents the electric conductivity of a volume enclosed by the nodes (i, j, k), (i+1, j, k), (i, j+1, k), (i+1, j+1, k), (i, j, k+1), (i+1, j, k+1), (i, j+1, k+1) and (i+1, j+1, k+1). For instance, σ(3, 3, 4) stands for conductivity of cube enclosed by nodes of (3,2,3), (3,3,3), (3,2,4), (3,3,4), (4,2,3), (4,3,3), (4,2,4), and (4,3,4). In addition, potential distributions corresponding to a point source of current are acquired by solving the Poisson equation using a direct and explicit finite difference technique for a half space with 3-D distribution of conductivity [4]. For the large sparse matrix, advantages of the bandwidth non-zero storage technique and incomplete Cholesky conjugate gradient method [5] are beneficial to be taken.

Fig. 1 Diagram of 3-D dividing

In the process of numerical simulation, through subtracting background potential from total potential [21], we can obtain abnormal potential as explained in Eq. (2):

φ_t-φ_b=φ_a                                    (2)

where φ_t symbolizes total potential; φ_b indicates background potential; φ_a signifies anomalous potential. Total potential and background potential are computed respectively by working out the Poisson equation.

In order to make anomalous potential much more evident, several mathematical algorithms are utilized selectively for different models. Firstly, the first-order differential operators can be gained by Eq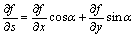. (3):

                       (3)

And then the solutions of the second-order differential operators are found through Eq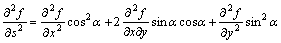. (4):

 (4)

Last but not least, we pay attention to the gradient operators as demonstrated in Eq. (5):

                         (5)

where α is made to depict the azimuth of differential coefficients and ||g|| indicates the gradient.

4 Simulation

As discussed before, in the previous numerical simulation, the resistivities have been calculated by Archie formula. While background resistivity ρ_b is calculated by the following relation: 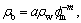 Otherwise, oil reservoir resistivity ρ_o can also be resolved utilizing the equation:  where the parameters are remarked individually as below: in view of practical situation, with the premises that formation water resistivity ρ_w=0.25 S/m [22]; matrix porosity is regarded as f_m=5%; reservoir porosity is considered as f_r=20%, and finally, water saturation in oil reservoir has the following hypothesis: S_w=10%. In the procedure of simulation, the modeling size is 8.0 km,  8.0 km and 4.0 km at x-direction, y-direction and z- direction, respectively.

4.1 Simulation 1

The oil layer with thickness of 400 m is located at the depth of 2 000-2 400 m in the model of three layers. In addition, a source with current of 20 A is set at the place 500 m far away from the well. Figure 2 displays the location relationship of Model 1 in detail. Figure 3 represents the anomalous electric potential from the well and Fig. 4 shows the first differential coefficient of anomalous electric potential. Hereinto, in Figs. 3 and 4, the shadow areas signify the oil layer. In Fig. 3, the anomalous phenomenon appears at the top of oil layer. However, two interfaces of the oil layer can be distinguished from Fig. 4. Hence, the results of Model 1 indicate that surface-borehole electric potential is feasible for layered formation and the first differential coefficient can greatly improve the solutions.

Fig. 2 Schematic diagram of Model 1

Fig. 3 Anomalous electric potential of Model 1

Fig. 4 First differential coefficient of electric potential of Model 1

4.2 Simulation 2

Compared with Model 1, Model 2 includes five layers and each vertical interval between two oil layers is 400 m. Figure 5 depicts Model 2 in detail. Figure 6 exhibits the anomalous electric potential of the well. However, it fails to offer a solution which can decide the position of each layer. Figure 7 displays the first differential coefficient of anomalous electric potential and it gives a desirable solution. Furthermore, the second differential coefficient provides a perfect solution as shown in Fig. 8, and the anomaly of electric potential is corresponding to the geo-electric layer.

Fig. 5 Schematic diagram of Model 2

Fig. 6 Anomalous electric potential of Model 2

4.3 Simulation 3

In order to check the influence of water layer on the oil layer, Model 3 and Model 4 are chosen to do the simulation. In Model 3, the water layer is under the oil layer, and oppositely, the water layer is over the oil layer in Model 4. Figures 9 depicts the Model 3 in detail. Figure 10 exhibits the anomalous electric potential of Model 3. Moreover, the first differential coefficient of anomalous electric potential and the second differential coefficient of anomalous electric potential are shown in Figs. 11 and 12, respectively. Additionally, Fig. 13 depicts the Model 4 and Figs. 14-16 display anomalous electric potential, the first differential coefficient and the second coefficient of Model 4, respectively. By comparing these results, we can easily find that the resolutions of Model 3 are much better than those of Model 4. Hence, we can conclude that the situation in which water layer is under the oil layer plays a positive role in exploration. However, the situation in which water layer is over the oil layer does play a negative role in exploration.

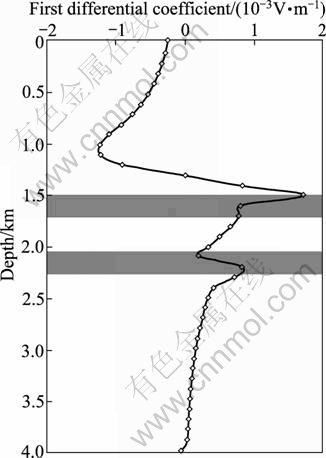
Fig. 7 First differential coefficient of electric potential of Model 2

Fig. 8 Second differential coefficient of electric potential of Model 2

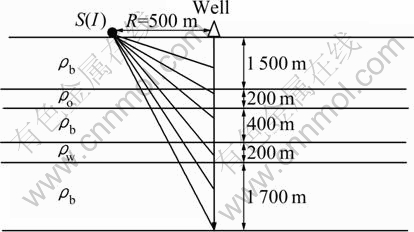
Fig. 9 Schematic diagram of Model 3

4.4 Simulation 3

The purpose of this work is to explore the measuring radius of surface-borehole electric potential. As shown in Fig. 17, Model 5 has three layers and the oil layer with thickness of 200 m is located at the depth from 2 100 m to 2 300 m. Distance from the well to oil layer is r.

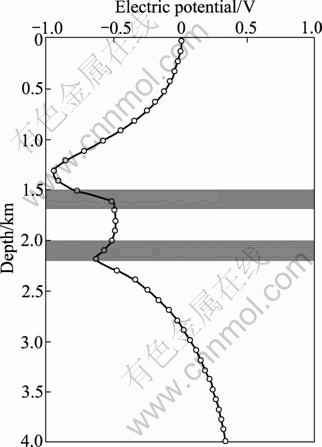
Fig. 10 Anomalous electric potential of Mode1 3

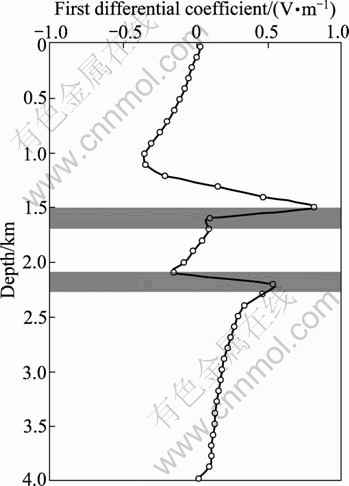
Fig. 11 First differential coefficient of electric potential of Mode1 3

Fig. 12 Second differential coefficient of electric potential of Mode1 3

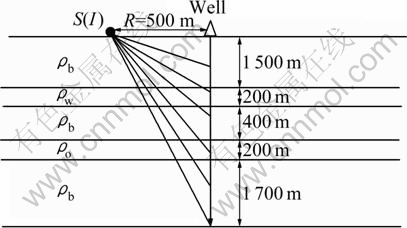
Fig. 13 Schematic diagram of Model 4

Fig. 14 Anomalous electric potential of Mode1 4

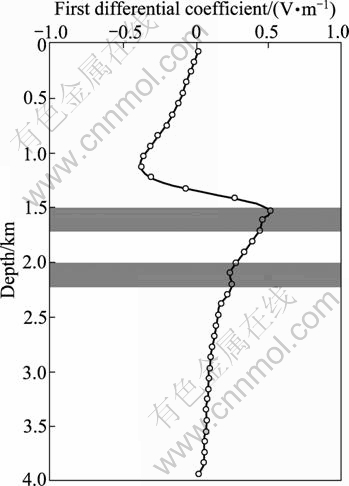
Fig. 15 First differential coefficient of electric potential of Mode1 4

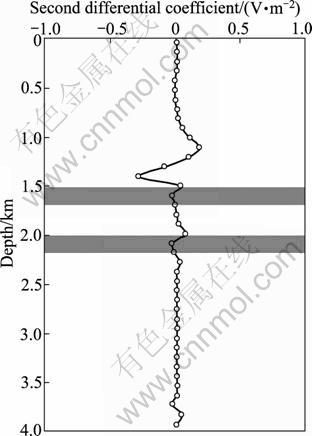
Fig. 16 Second differential coefficient of electric potential of Mode1 4

Fig. 17 Schematic diagram of Model 5

Figure 18 shows the anomalous electric potential of this model. Furthermore, the first coefficient and the second coefficient are shown in Figs. 19 and 20, respectively. Attention should be paid to these three figures as they demonstrate that with the increase of distance, the resolutions decrease. Especially, compared with the resolutions of 200 m and 400 m measuring radii, the second coefficient of 600 m cannot provide useful information any more.

Fig. 18 Anomalous electric potential of Mode1 5

Fig. 19 First differential coefficient of electric potential of Mode1 5

5 Conclusions

1) The method of surface-borehole electric potential can acquire abnormities of electric potential which are available corresponding to geo-electric layers. Moreover, application of the first coefficient operator and the second coefficient operator can improve resolutions greatly.

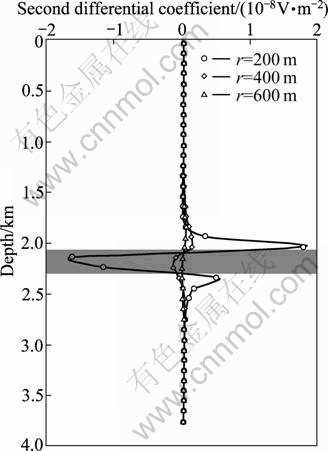
Fig. 20 Second differential coefficient of electric potential of Mode1 5

2) As for layered formation, if the water layer is above the oil layer, it will have a strong shielding effect on the bottom oil layer. Hence, it plays a negative role in distinguishing oil layer from formation. Nevertheless, in the case of water layer below the oil layer, water layer will improve the resolution of recognizing oil layer. Therefore, when the water layer is placed below the oil layer, it will have a positive effect on the oil exploration.

3) With the increase of distance, the resolution will decrease. However, the measuring radius is effective enough for oil production.

References

[1] SILL W R, WARDS S H. Electrical energizing of well casing: Final report [D]. Department of Geology and Geophysics University of Utah, 1978.

[2] STIERMAN D J. Electrical methods of detecting contaminated groundwater at the Stringfellow waste disposal site, Riverside County, California [J]. Environ Geol Water Sci, 1984, 6(1): 1-20.

[3] USHIJIMA K, MIZUNAGA H, TANAKA T. Reservoir monitoring by a 4-D electrical technique [J]. The Leading Edge, 1999, 18(12): 1422-1424.

[4] DEY A, MORRISON H F. Resistivity modeling for arbitrarily shaped three dimensional structures [J]. Geophysics, 1979, 44(4): 753-780.

[5] WU Xiao-ping, XU Guo-ming. 3-D resistivity forward calculation accelerated by ICCG iteration technique [J]. Coal Geology and Exploration, 1999: 62-66. (in Chinese)

[6] WANG Zhi-gang, HE Zhan-xiang, WEI Wei-bo, DEN Ming. The three dimensional physical model experiment research of borehole-ground electric method [J]. Oil Geophysical Prospecting, 2005, 40(5): 594-597. (in Chinese)

[7] WANG Zhi-gang, HE Zhan-xiang, LIU Yi. Research of three-dimensional modeling and anomalous rule on borehole—Ground DC method [J]. Chinese Journal of Engineering Geophysics, 2006, 3(2): 87-92. (in Chinese)

[8] GUO Wen-bo, SONG Jing-ping, LI Xiu, XUE Guo-qiang, FAN Jin-sheng. Numerical calculation of borehole electrical survey in layered media and its applications [J]. Chinese Journal of Geophysics, 2006, 49(5): 1561-1566. (in Chinese)

[9] HE Zhan-xiang, LIU Xue-jun, QIU Wei-ting, ZHOU Huang. Mapping reservoir boundary by using borehole-surface TFEM technique [C]// 74th Ann Soc Expl Geophys, Expanded Abstracts Two Case Studies, Denvor: 2004: 10-15.

[10] LIU H, WANG Z, HE Z X. Frequency-domain 3D borehole-surface electromagnetic modeling by the volume integral equation method [C]// 70th EAGE Conference & Exhibition A, 2008: 9-12.

[11] PARASNIS D S. Three-dimensional electric mise-a`-la-masse survey of an irregular lead–zinc–copper deposit in central Sweden [J]. Geophys Prospect, 1967, 15(3): 407-437.

[12] SHEN Jing-song, SUN Wen-bo. 2.5-D modeling of cross-hole electromagnetic measurement by finite element method [J]. Petroleum Science, 2008, 5: 126-134.

[13] SHEN Jing-song, SUN Wen-bo. Application of 2.5-D cross-hole electromagnetic inversion in Gudao Oil Field, East China [J]. Applied Geophysics, 2008, 5(3): 159-169.

[14] LI Jian-hui, ZHU Zi-qiang, FENG De-shan, XIAO Jian-ping, PENG Ling-xing. Calculation of all-time apparent resistivity of large loop transient electromagnetic method with very fast simulated annealing [J]. Journal of Central South University of Technology, 2011, 18: 1235-1239.

[15] SU Jian-jun. Research on the principle and method of cross-well e1ectromagnetic logging and the rule of the influence of casing on cross-we11 e1ectromagnetic logging [D]. Qingdao: Ocean University of China, 2004. (in Chinese)

[16] HE Fan. Application of test technique of cross-well electrical potential in Daqing oilfield [J]. Petroleum Instruments, 2009, 23(3): 63-68. (in Chinese)

[17] ARCHIE G E. The electrical resistivity log as an aid in determining some reservoir characteristics [J]. Tnas Am Inst Mech Eng, 1942, 146: 54-61.

[18] NIWAS S, GUOTA P K, OLIVAR A L. Nonlinear electrical response of saturated shaley sand reservoir and its asymptotic approximations [J]. Geophysics, 2006, 71(3): G129-G133.

[19] BUSSIAN A E. Electrical conductance in a porous medium [J]. Geophysics, 1983, 48(5): 1258-1268.

[20] DAVID K. The porosity-water saturation-conductivity relationship: An alternative to Archie’s Model [J]. Petrophysics, 2007, 48(5): 335-361.

[21] XU Shi-zhe, LIU Bo, RUAN Bai-rao. The finite element method for solving anomalous potential for resistivity surveys [J]. Chinese Journal of Geophysics, 1994(S2): 511-515. (in Chinese)

[22] SHEN Jing-song, SU Ben-yu, GUO Nai-chuan. Anisotropic characteristics of electrical responses of fractured reservoir with multiple sets of fractures [J]. Petroleum Science, 2009, 6(2): 127-138.

(Edited by HE Yun-bin)

Foundation item: Project supported by Global Center of Excellence in Novel Carbon Resource Sciences, Kyushu University, Japan

Received date: 2011-08-19; Accepted date: 2011-10-28

Corresponding author: SU Ben-yu, PhD; Tel: +80-3906-5518; E-mail: subenyu@yahoo.cn