Hot compression deformation characteristics of Mg-Mn alloys

FANG Chao(方 超)¹, ZHANG Jing(张 静)^{1, 2}, LIAO Ai-lin(廖爱林)¹,

 XUE Shao-zhan(薛绍展)¹, YUAN Fu-qing(袁付庆)¹, PAN Fu-sheng(潘复生)^1,2

1. College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China;

2. National Engineering Research Center for Magnesium Alloys, Chongqing 400044, China

Received 15 November 2009; accepted 12 March 2010

Abstract：The hot deformation behaviors of solution treated Mg-1.8Mn-0.4Er-0.2Al alloys were investigated by means of compression tests on Gleeble-1500 in strain rate range of 0.01-10 s^-1, deformation temperature range of 250-450 °C and a true strain of 0.6. The constitutive relationships among flow stress, strain rate and deformation temperature were described by Arrhenius-type equations, based on the fact that the material constants could be calculated under a wide range of strains. The results show that the flow stress of the experimental alloy decreases with temperature increasing and strain rate decreasing. Under the experimental conditions, the products of constant α and n in the constitutive equation are stable within certain strains, and the deformation activation energy ranges from 160 to 220 kJ/mol. It is proved that the values of calculated flow stress are close to the experimental results with average error of 2.01%.

Key words: magnesium alloy; thermal deformation; flow stress; constitutive equation

1 Introduction

Magnesium alloys are receiving much attention for their excellent properties, such as low density, good thermal and electrical conductivity, electromagnetic shielding ability, as well as attractive appearance[1]. Especially, magnesium alloys have a great potential for wide applications in the automotive industry to lighten weight, which is significant for reduction of greenhouse gas emissions and the fuel cost of transportation[2].

Owing to the hexagonal close-packed crystal structure, magnesium alloys have few slip systems at room temperature, resulting in a low formability. So, magnesium alloy products are mainly shaped by high pressure die casting. However, wrought magnesium alloys undergoing hot deformation have superior properties, for example, higher strength and better ductility, which makes it possible to meet the need of various structures[3-6].

Up to now, related researches are mostly carried out on AZ magnesium alloy system. LUAN et al[7] have corrected the flow stresses of AZ80 alloys obtained from the compression tests, calculated the constants of constitutive equation, and concluded that the size of recrystallized grains grows with the Zener-Hollomon parameter increasing. SLOOFF et al[8] studied the variation law of thermal flow stresses of AZ61, detailed the methods of calculating the constants of constitutive equation, and tried to explore how these constants influence the flow stresses. Moreover, CERRI et al[9] analyzed the different deformation behaviors of AZ91 magnesium alloys after high pressure die casting and solution treatment, and discussed the discrepancy between two experimental alloys.

Mg-Mn system alloy is one of the early commercially used wrought magnesium alloys, having sound welding property, corrosion-resistance and modest strength[10]. Compared with other wrought magnesium alloys, the studies on Mg-Mn system alloy are still far from the average level[11-12]. Rare earth elements have been described as industrial monosodium glutamate which can improve the performance of the magnesium alloy. According to Refs.[13-14], rare earth elements Er and Al can form Al₃Er compound, having high melting point, which can act as a non-homogeneous core in the process of nucleation. Thus, it may increase the nucleation rate and refine the grain.

In the present work, Mg-1.8Mn-0.4Er-0.2Al alloys with different heat treatments were chosen. The alloys were hot uniaxial compressed on Gleeble-1500 thermo-mechanical simulator. The constitutive relationship of the material was portrayed by Arrhenius equations, and the material constants were calculated by the data obtained from the compressing tests.

2 Experimental

The composition of the experimental alloy is Mg-1.8Mn-0.4Er-0.2Al (mass fraction, %). Commercial high-purity Mg (>99.9%) and Al (>99.95%), and master alloys Mg-4.4%Mn and Mg-30%Er were used to prepare the alloys, by semi-continuous casting into bar ingots of 85 mm in diameter. Cylindrical specimens with a diameter of 10 mm and a height of 12 mm were machined from the ingots. Solution treatments were performed before compression test in order to eliminate the dendrite in cast microstructure and obtain some typical alloys with different microstructures. The samples were solution treated at 450 °C for 2, 4 and 8 h, denoted as In.A, In.B and In.C, respectively. Then, uniaxial compression test for hot workability analysis was performed on a Gleeble-1500 machine at strain rate ranging from 0.01 to 10 s^-1 and at an initial temperature between 250 and 450 °C. The samples were heated at 10 °C/s and kept for 30 s at the preset temperature before hot uniaxial compressing to a true strain of 0.6. A thermocouple was spot welded onto the surface of sample in order to measure and control the temperature. To minimize the friction between sample and anvil of the holder during hot deformation, graphite foils were used as lubricant. The deformation temperature, stress, strain and strain rate during the testing were automatically recorded. After the deformation, samples were quenched in water at around 70 °C.

3 Results and discussion

3.1 True strain-true stress curves

Figure 1 shows the flow stress-strain curves of experimental alloys at different deformation conditions.

It is seen from Fig.1 that, flow stresses in the experiments decrease with temperature increasing and strain rate decreasing. In the first deformation period, the flow stresses rise with strain increasing rapidly, illuminating that the work-hardening plays the major role. With the deformation process going on, the curves exhibit two main shapes. One is close to level after peak

Fig.1 True stress-true strain curves for Mg-1.8Mn-0.4Er-0.2Al alloys under various deformation conditions: (a) In.A, 0.1 s^-1; (b) In.B, 1 s^-1; (c) In.C, 250 °C; (d) In.C, 350 °C

stress, especially when the strain rate is low or the temperature is high, showing that the stress reaches steady state. This is called steady-state rheological behavior. And in this state, a balance appears between work-hardening and flow softening of recrystallization. The other becomes descended after the peak stress, indicating the beginning of recrystallization, leading to the fact that the effects of flow softening exceed that of work-hardening. It can also be seen that the flow stress curves wave at the stain rate of 0.1 s^-1. This phenomenon stands for discontinuous recrystallization of alloys, which corresponds to inhomogeneous deformation causing alloy cracking.

3.2 Constitutive equation correction and constants calculation

Besides temperature, strain rate also has great impact on plastic behavior of magnesium alloy during hot deformation process. Hot deformation process is similar to elevated temperature creep, having a pronounced characteristic that strain rate is controlled by thermal activation process, which follows the Arrhenius equation. At present, three forms of Arrhenius-type constitutive equations are commonly used to describe the metal flow stresses[15]:

1) Low stress state

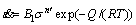                       (1)

2) High stress state

                  (2)

3) All stress state

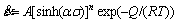                 (3)

where B₁, B₂ ,, n, α, β and A are material constants, Q is the activation energy of deformation, and R is the universal gas constant. The stress multiplier α is an adjustable constant and an optimum α value should be found, when the constant T curves in the ln[sinh(ασ)] against ln plots are almost linear and parallel with each other.

The raw data from Gleeble-1500 system are not suitable for immediate constitutive analysis because the temperature of samples in the process of hot deformation has some deviations corresponding to the pre-set temperature due to thermal deformation effects. That is to say, the stresses experimentally measured are not the ones of pre-set temperature. Solving the constants of constitutive equation needs true stress-true strain curves at constant temperature, so the measured stresses should be corrected by Eqs.(1) and (2) under low and high stress state, respectively. When strain rate and strain are low, the sample temperature approximately maintains constant, which means that the corrected stresses equal the measured ones. So, in this work, the flow stresses just under higher strain rate and higher strain are corrected using Eq.(2)[16].

The logarithmic transformation for Eq.(2) is

                     (4)

The correction of flow stress for deformation heating was accomplished by plotting σ against 1/T for each selected strain rate, and then was extrapolated back to the pre-set testing temperatures. Fig.2 shows the comparison between the corrected and the uncorrected flow curves. It can be seen that at higher temperature of 450 °C, the differences between the corrected and the uncorrected flow stresses are indeed insignificant. At lower temperature of 250 °C, the differences become a little apparent and the values of corrected stresses are slightly higher than the uncorrected ones. The differences between the two are no more than 6 MPa and the characteristic of the flow curves is basically unchanged.

Fig.2 Corrected and uncorrected true stress-true strain curves of In.C alloy

With the corrected stress at each strain, the constitutive equation in the form of Eq.(3) could be established. Taking logarithmic form, the re-arranged Eq.(3) is obtained:

            (5)

The aim of introducing the adjustable constant α is to make the constant n little impacted by temperature, through choosing an optimal value of α. Thus, n is suitable for all experimental temperatures. At constant temperature, the parallel relationship among the curves of plotting ln[sinh(ασ)] against  is little influenced by α. And the reason that the curves of plotting ln[sinh(ασ)] against  are not parallel, is caused by experimental data.

It is determined that the value of α ranges from 10^-6 to 1, and the optimum is found out utilizing C language programs. Through a large number of experimental data processing, it is found that the linear correlation among the curves of plotting  against  is little affected by changing the value of α. Hence, the parallel degree decides the optimal value of α. Plots of  against  at selected values of strain and three pre-set temperatures are shown in Fig.3. When the three lines of 523 K, 623 K, 723 K are pretty closed to parallel, the optimal value of α can be obtained.

Fig.3 Relationship between true stress, strain rate and temperature at strain of 0.15 during plastic deformation of In.A alloy: (a) , b)

Rearranging Eq.(5) and differentiating with respect to 1/T gives an expression for the activation energy Q:

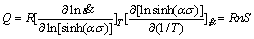     (6)

It can been seen from Fig.3(a) that the slop of the  against  plot gives the value of 1/n. S is the average slope of the lines in the  against 1/T plots, as shown in Fig.3(b). The activation energy Q can be calculated using Eq.(6).

The intercept of the ln[sinh(ασ)] against  is the value of , where Q, R, T are known, so the value of ln A can be obtained. The values of the constitutive constants at selected strains are given in Table 1.

It can be seen from Table 1 that, the value of α fluctuates around 0.1 and n is in the range from 1.9 to 5.0. However, the values of Q and ln A decrease slowly and keep a stable value in the middle strains, indicating that the deformation reaches a steady state. During the processing of obtaining the optimal value of α, the following findings can be seen. 1) The value of α fluctuates in certain ranges, which slightly impacts the parallel degree among the lines of plotting against , so it is acceptable that the value of α is around 0.1; 2) The value of n varies oppositely with α, which is coincided with the work of SLOOFF et al[8]; 3) The products of α and n are constant within certain strains, as shown in Fig.4. The activation energies Q of In.A, In.B and In.C are 220, 160 and 200 kJ/mol, respectively, which are higher than the self-diffusion energy of magnesium. The reason should be related to the microstructure. As for the cause of the decrease of Q value, according to SLOOFF et al[8], during hot deformation of magnesium, dynamic recrystallization takes place; while deformation proceeds, new grains are formed. Thus, an increased number of grain boundaries enhance diffusion.

The values of flow stresses at each strain can be calculated through taking these material constants into

Table 1 Constitutive constants of In.A alloy obtained from corrected flow stresses at selected strains

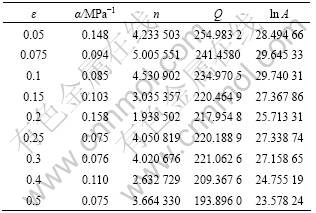
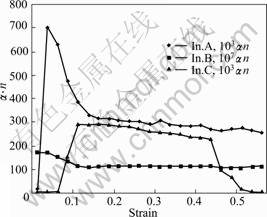
Fig.4 Relationship between strain and (α?n) value

Eq.(3). Fig.5 shows the comparison between the calculated and the measured stresses of In.A at all deformation conditions. It can be concluded that the largest error is no more than 5.11% and the average error is about 2.01%, demonstrating that the method of this work used to simulate the flow stress at elevated temperature has higher accuracy.

Fig.5 Comparison between calculated and measured flow stresses

4 Conclusions

1) The flow stresses of wrought magnesium alloy Mg-1.8Mn-0.4Er-0.2Al at hot compression test decrease with increasing deformation temperature and decreasing strain rate. In the experiment, dynamic recrystallization occurs in the alloy.

2) The flow stress curves wave at the strain rate of 0.1 s^-1, indicating discontinuous recrystallization occurs in the experimental alloy.

3) The material constants are dependent on strain. But, the products of constitutive constants α and n are constant within certain strains, which is coincided with the variation trend of Q and ln A.

4) The deformation activation energy of the three different experimental alloys are 220, 160 and 200 kJ/mol, respectively. The values of the calculated flow stress are close to the experimental results with average error of 2.01%.

References

[1] YANG Z, LI J P, ZHANG J X, LORIMER G W, ROBSON J. Review on research and development of magnesium alloys [J]. Acta Metallurgica Sinica (English letters), 2008, 21(5): 313-328.

[2] MARK E, AIFEN B, MATTHEW B. Magnesium alloy applications in automotive structures [J]. JOM, 2008, 60(11): 57-62.

[3] MORDIKE B L. Magnesium and magnesium alloys [J]. Light Metals, 2001, 51: 2-15.

[4] LIU Zheng, ZHANG Kui, ZENG Xiao-qin. The theory and application of Mg-based light alloy [M]. Beijing: China Machine Press, 2002. (in Chinese)

[5] ELIZER D, AGHION E, FROES F H. Recent magnesium developments [C]//Synthesis of Lightweight Metals III. San Diego, CA: The Minerals, Metals & Materials Society, 1999. 139-153.

[6] CAHN R. Structure and properties of nonferrous alloys [M]. DING Dao-yun, GAN Fu-xi, YE Heng-qiang, transl. Beijing: Science Press, 1999: 105. (in Chinese)

[7] LUAN Na, LI Luo-xing, LI Guang-yao, ZHONG Zhi-hua. Hot compression deformation behaviors of AZ80 magnesium alloy at elevated temperature [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(10): 1678-1684. (in Chinese)

[8] SLOOFF F A, ZHOU J, DUSZCZYK J, KATGERMAN L. Constitutive behavior of wrought magnesium alloy AZ61 [C]//Proceedings of Magnesium Technology 2007. TMS, 2007: 363-368.

[9] CERRI E, LEO P, DE MARCO P P. Hot compression behavior of the AZ91 magnesium alloy produced by high pressure die casting [J]. Journal of Materials Processing Technology, 2007, 189: 97-106.

[10] WENG Kang-rong, LI Yong-gang, WANG Song-jie, ZHAO Hong-liang, GUAN Shao-kang. The microstructure and mechanical properties of Mg-1.6Mn-1.5Si-0.3Ca alloy [J]. Light Alloy Fabrication Technology, 2007, 35(5): 41-43. (in Chinese)

[11] YU Kun, LI Wen-xian, WANG Ri-chu, MA Zheng-qing. Research, development and application of wrought magnesium alloys [J]. The Chinese Journal of Nonferrous Metals, 2003, 13(2): 277-288. (in Chinese)

[12] WENG Kang-rong, ZHAO Hong-yan, ZHOU Zhan-xia, ZHAO Hong-liang. Influence of Si, Ca on microstructure and properties of Mg-2Mn Alloy [J]. Hot Working Technology (Casting and Forging), 2006, 35(1): 1-3. (in Chinese)

[13] XU Guo-fu, YANG Jun-jun, JIN Tou-nan, NIE Zuo-ren, YIN Zhi-min. Effects of trace erbium on structure and properties of Al-5Mg alloy [J]. The Chinese Journal of Nonferrous Metals, 2006, 16(5): 768-774. (in Chinese)

[14] YANG Jun-jun, NIE Zuo-ren, JIN Tou-nan, RUAN Hai-qiong, ZUO Tie-yong. Form and refinement mechanism of element Er in Al-Zn-Mg alloy [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(4): 620-626. (in Chinese)

[15] McQUEEN H J, BELLING J. Constitutive constants for hot working of Al-4.5Mg-0.35Mn(AA5182) [J]. Canadian Metallurgical Quarterly, 2000, 39(4): 486-492.

[16] LI L, ZHOU J，DUSZCZYK J. Determination of a constitutive relationship for AZ31B magnesium alloy and validation through comparison between simulated and real extrusion [J]. Journal of Materials Processing Technology, 2006, 172: 372-380.

(Edited by YANG Bing)

Foundation item: Project(2008BA4036) supported by the Natural Science Foundation of Chongqing Science and Technology Commission, China; Project(081061130) supported by the National University Students Research Training Program and Sharing Fund of Chongqing University’s Large-scale Equipment

Corresponding author: ZHANG Jing; Tel: +86-23-65111167; Fax: +86-23-65102821; E-mail: jingzhang@cqu.edu.cn

DOI: 10.1016/S1003-6326(09)60383-6