泡壁材料性能对泡沫铝压缩性能的影响
来源期刊:中国有色金属学报(英文版)2015年第5期
论文作者:袁建宇 李言祥
文章页码:1619 - 1625
关键词:泡沫铝;泡沫材料性能;单向压缩性能;有限元分析
Key words:aluminum foams; cell wall property; uniaxial compressive performance; FE analysis
摘 要:针对吹气法制备的高孔隙率闭孔泡沫铝,通过实验和有限元分析研究泡壁材料性能对其压缩性能的影响。向添加陶瓷颗粒的A356合金熔体中吹气发泡制备实验样品并进行单向压缩。通过光学显微镜和扫描电镜观察泡壁的微观组织和断口组织。结果表明,泡壁中存在的颗粒团聚、孔洞等缺陷和氧化膜削弱了其性能,因此,泡沫材料的性能与原材料性能有很大差别。基于原材料性能和实体材料性能的实验结果,对泡沫铝理想三维结构进行有限元分析。材料的平台应力与泡沫材料的屈服强度成正比。有限元模拟结果稍高于实验结果,其部分原因是将实体材料性能看做泡壁材料性能导致的。
Abstract: The effects of cell wall property on the compressive performance of high porosity, closed-cell aluminum foams prepared by gas injection method were investigated. The research was conducted both experimentally and numerically. Foam specimens prepared from conditioned melt were tested under uniaxial compressive loading condition. The cell wall microstructure and fracture were observed through optical microscope (OM) and scanning electron microscope (SEM), which indicates that the cell wall property is impaired by the defects in cell walls and oxide films on the cell wall surface. Subsequently, finite element (FE) models based on three-dimensional thin shell Kelvin tetrakaidecahedron were developed based on the mechanical properties of the raw material and solid material that are determined by using experimental measurements. The simulation results show that the plateau stress of the nominal stress-strain curve exhibits a linear relationship with the yield strength of the cell wall material. The simulation plateau stress is higher than the experimental data, partly owing to the substitution of solid material for cell wall material in the process of the establishment of FE models.
Trans. Nonferrous Met. Soc. China 25(2015) 1619-1625
Jian-yu YUAN1, Yan-xiang LI1,2
1. School of Materials Science and Engineering, Tsinghua University, Beijing 100084, China;
2. Key Laboratory for Advanced Materials Processing Technology, Ministry of Education, Tsinghua University, Beijing 100084, China
Received 16 April 2014; accepted 20 June 2014
Abstract: The effects of cell wall property on the compressive performance of high porosity, closed-cell aluminum foams prepared by gas injection method were investigated. The research was conducted both experimentally and numerically. Foam specimens prepared from conditioned melt were tested under uniaxial compressive loading condition. The cell wall microstructure and fracture were observed through optical microscope (OM) and scanning electron microscope (SEM), which indicates that the cell wall property is impaired by the defects in cell walls and oxide films on the cell wall surface. Subsequently, finite element (FE) models based on three-dimensional thin shell Kelvin tetrakaidecahedron were developed based on the mechanical properties of the raw material and solid material that are determined by using experimental measurements. The simulation results show that the plateau stress of the nominal stress-strain curve exhibits a linear relationship with the yield strength of the cell wall material. The simulation plateau stress is higher than the experimental data, partly owing to the substitution of solid material for cell wall material in the process of the establishment of FE models.
Key words: aluminum foams; cell wall property; uniaxial compressive performance; FE analysis
1 Introduction
Over the past decades, there has been interest in aluminum foams as a kind of light weight energy absorption material with great potential for applications in automobiles, high speed trains and other vehicles [1,2]. The compressive performance of aluminum foams has thereby fascinated many researchers by both numerical and experimental studying. In many numerical studies, ideal models based on Kelvin tetrakaidecahedron were used [3] for their good characterization of high porosity aluminum foams. However, it is now recognized that the simulation results are usually larger than the experimental data due to the irregularity of cell structure and the impaired mechanical property of cell wall material [4,5].
The main concern of many studies is focused on the modeling of the cell structure of foamed metals by developing different kinds of three-dimensional finite element models. SIMONE and GIBSON [6,7] studied the effects of cell wall curvature and corrugations as well as solid distribution between cell edge and cell wall on the stiffness and strength of metallic foams. MEGUID et al [8] studied the crush behavior of closed-cell metallic foams with varying spatial density distribution. LU et al [9] studied the influence of missing cell struts, filled cell faces and curved cell struts on the compressive performance of open-cell metallic foams. de GIORGI et al [10] developed Kelvin cells with both plane and curved walls and ellipsoidal cells defined by random dimension, position and orientation to obtain the stress-strain curves of aluminum foams.
The construction of specific cell structure is often highlighted in previous publications, and it is acknowledged that the cell wall curvature, cell wall corrugation, inhomogeneous distribution between cell edge and cell wall, inhomogeneous spatial density distribution, holes in cell wall and missing cell face or cell edge significantly affect the compressive performance of aluminum foams. However, limited references covered the effects of different cell wall material properties on the compressive performance of aluminum foams. JEENAGER and PANCHOLI [11] studied the influence of cell wall microstructure developed through solutionizing and quenching followed by the thermal ageing treatment on the energy absorption capability of aluminum foams produced by melt foaming method. CAMPANA and PILONE [12] investigated the effect of cell wall microstructure by compact powder technology starting from 7075, 6061 and AlSi7 alloys on the crush behavior of Al alloy foams. JEON et al [13,14] did some work on the cell wall mechanical properties of closed-cell Al foams with X-ray computed tomography. TODA et al [15] used high-resolution synchrotron X-ray tomography for the characterization of microstructure in the cell walls. All the above analysis suggested that besides three-dimensional cell structure, the cell wall microstructure and properties have significant influence on the compressive performance of aluminum foams.
This work mainly concerns the effects of cell wall property on the compressive performance of aluminum foams. Research was done both experimentally and numerically. The simulation results were compared with experimental data obtained through quasi-static uniaxial compressive loading.
2 Experimental
The aluminum foam specimens were fabricated by dispersing 10% 10 μm Al2O3 powder (volume fraction) into commercial A356 alloy melt to stabilize the foams. Compressed air was introduced into the melt through an orifice submerged at the bottom of the crucible to produce aluminum foams. Figure 1 shows the topologies of closed cell aluminum foams in the transverse and longitudinal sections. It is affirmed that the cell is anisotropic due to the liquid state cell deformation caused by gravity. The anisotropy ratio can be defined as the transverse cell size over the longitudinal cell size. It varies from 1 to 2 in the present research. The microstructure was examined on a Neophot 32 optical microscope. The fracture of the cell wall after compressive tests was observed with an FEI Quanta 200 FEG scanning electron microscope using an accelerating voltage of 10 kV. The surface of the cell wall was observed using an accelerating voltage of 15 kV. The compressive test of aluminum foams was conducted on a WDW-100 computer-controlled electronic universal testing machine. The compressive rate was 5 mm/min and the load-displacement curves were recorded automatically. The size of the cylindrical foam specimens was d80 mm × 100 mm.
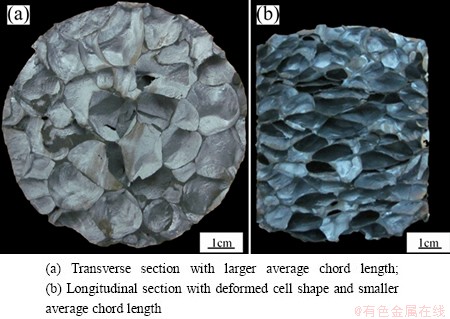
Fig. 1 Topologies of high porosity closed-cell aluminum foams
3 Results and discussion
3.1 Cell wall microstructure
Figure 2 shows the difference of raw material, solid material and cell wall material of aluminum foams in the preparation process. The raw material is the commercial A356 alloy. The solid material is the melt stabilized by ceramic particles for foaming. The cell wall material is different from the solid material because the existence of oxide film on the cell wall surface and defects in the cell wall microstructure.
Figure 3 shows the microstructures of the raw material, solid material and cell wall material in the current work. It can be seen that the microstructure of raw material, solid material and cell wall material exhibited huge difference due to the difference in solidification condition, composition and particle distribution. Figure 3(a) shows the microstructure of the commercial A356 alloy. If ceramic powder was added and dispersed in the melt, particle aggregation and pores can be observed, which can significantly impair the mechanical property of the solid material, as shown in Fig. 3(b). Although the microstructure of cell wall material and solid material is similar as shown in Fig. 3(c), the mechanical property is different because the existence of oxide film on the cell wall surface and the difference of solidification conditions. Moreover, since the size of pores and particle aggregations are in the same order of magnitude with the sizes of cell wall thickness (50-200 μm) [16], the influence of pores and aggregations is more significant on cell wall material than on solid material.

Fig. 2 Composition and characteristics of raw material, solid material and cell wall material
The deformation mechanism of cell wall can be illustrated as both ductile and brittle according to Fig. 4. Figure 4(a) shows the evidence of dimple rupture and indicates the plastic stretching of the cell wall. Figure 4(b) shows the cleavage fracture as a sign of brittle rupture. Figure 4(c) shows the fracture microstructure of particle aggregation that promotes the brittle rupture behavior of the cell wall material. The surface of the cell wall is covered with thin oxide film with wavy morphology as shown in Fig. 4(d).

Fig. 3 Microstructures of A356 raw material with no ceramic particle addition (a), A356+10% Al2O3 solid material with pores and particle aggregations (b) and cross-section of lamellar cell wall material (c)
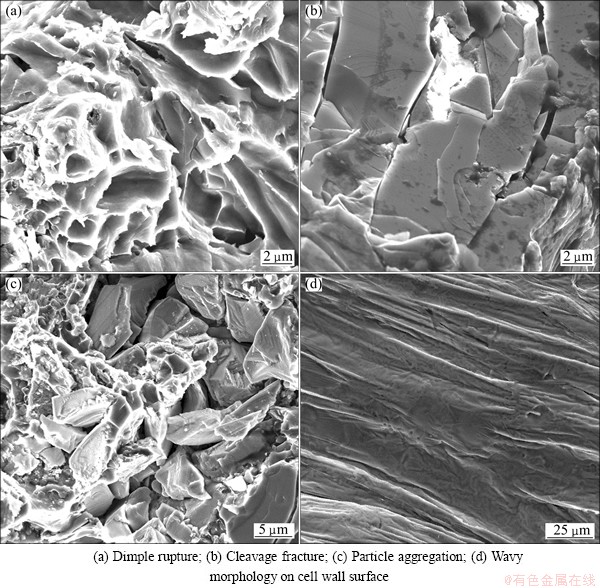
Fig. 4 Cell wall microstructures after uniaxial loading
Owing to the special fracture microstructure in the cell wall and the oxide films on the cell wall surface, the property of the cell wall material is significantly different from the property of raw material or solid material. From OM and SEM observations, it is concluded that the cell wall material shows more brittle behavior that plays an important role in the compression behavior of aluminum foams. However, the property of cell wall material is difficult to be determined because it is hard to test the mechanical properties by utilizing a tiny chip of the cell wall. Although JEON et al [13] determined the cell wall mechanical properties by comparing the computed force-displacement curves with the measured ones, that method relies on precise characterization of the cell structure by using X-ray tomography. Therefore, in the following establishment of the finite element model, the mechanical properties of raw material and solid material are utilized as an approximation of the property of cell wall material. The consequence of the approximation is discussed later.
3.2 Uniaxial compression test
For an ideal Kelvin tetrakaidecahedron, the relative density can be expressed as
 (1)
(1)
where the cell anisotropy ratio δ, which is defined as the length ratio of transverse axis to longitudinal axis, is considered. ρ* is the density of aluminum foams and ρs is the density of the corresponding solid material, t is the cell wall thickness and l is the cell edge length of the tetrakaidecahedron.
Figure 5 illustrates some typical nominal stress- strain curves in the compression test. The plateau stress ρ*pl of the aluminum foams is determined from the curves as
 (2)
(2)
where εd is the densification strain, σ and ε are the nominal stress and strain, respectively.

Fig. 5 Typical nominal stress-strain curves with relative density of 0.026-0.173 based on uniaxial compression tests
3.3 Finite element model
Figure 6(a) shows the Kelvin tetrakaidecahedron model developed based on the actual cell geometry. Figures 6(b)-(d) show the contours of effective stress during the deformation process, which suit well with the experimental results. A multiple cell finite element model which employs 64 unit cells with a total 15502 shell elements was used to describe the deformation characteristics of multi-layer structure. The Belytschko- Tsay shell element with hourglass control and self-contact was used. The upper rigid plane was fixed all degrees of freedom except for the loading direction while the lower plane was fixed all degrees of freedom. Automatic surface-to-surface contact was invoked between the cells and the rigid planes. The upper plane was loaded at a speed of 0.1 m/s. The compression simulation test ceased at the strain of about 0.7. The boundary conditions applied to the foam cells were the kinematic contact constraints. The h-adaptive method was used to split bigger elements into smaller ones when the elements experienced large distortion. The LS-prepost commercial software was used to analyze the simulation data.
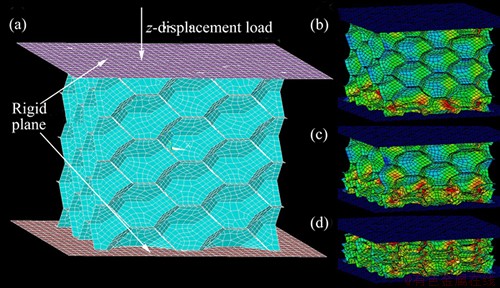
Fig. 6 Finite element model based on Kelvin tetrakaidecahedron (a) and contours of effective stress during deformation process with nominal strains of 0.1 (b), 0.3 (c) and 0.5 (d)
There are limited references focusing the property of cell wall material, so the material model for cell wall in finite element analysis did not attach much attention. Many researchers employed the elastic perfectly plastic model for the cell wall material, with isotropic hardening or kinematic hardening [17,18]. These models suit well for the cell wall material in small strain zones, therefore, the above mentioned references mainly focused on the elastic modulus of aluminum foams or the compressive behavior when the strain is less than 0.2. However, when it comes to the energy absorption capability of aluminum foams, the final strain can be as large as 0.7. For this reason, a piecewise linear plastic model for the cell wall material was used in this work. It was successfully adopted in earlier publications [8,19], and was found to be reasonable for the analysis of the deformation mechanism under big strain. The piecewise linear plastic model requires inputting the true stress and true strain, which can be obtained by the following equations:
 (3)
(3)
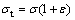 (4)
(4)
where σ and ε are the nominal stress and strain, respectively, σt and εt are the true stress and strain, respectively.
Uniaxial experiments were done to determine the true stress-strain curves of raw material and solid material. The curves are discretized as shown in Fig. 7. They serve as the material property data in the Ansys code. The density of all the materials is set as 2700 kg/m3 and Poisson ratio is 0.33. The elastic modulus is 70 GPa for raw material and solid material. The yield strengths for raw material and solid material are 209 MPa and 162 MPa, respectively.

Fig. 7 Discretized true stress-strain curves of raw material and solid material based on experimental measurements
3.4 Effects of cell wall property
The cell structure parameters for finite element models were selected based on observation and measurement of aluminum foam specimens. The cell wall thickness is 100 μm, the cell edge length of the Kelvin tetrakaidecahedron is 3.6 mm (the equivalent cell size is 10 mm), the cell anisotropy ratio is 1 and the relative density is calculated to be 0.033. Figure 8 shows the nominal stress-strain curves of aluminum foams for different base materials. The densification strain is similar in two cases and set to be 0.6. Thus, the plateau stress can be calculated as the average stress through nominal strain 0 to 0.6.
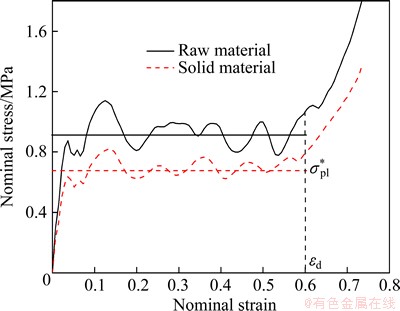
Fig. 8 Nominal stress-strain curves of finite element models corresponding to raw material and solid material
The plateau stresses of the two cases were calculated to be 0.91 MPa and 0.68 MPa. It was found to have a linear relationship with the yield strength of the composing materials. This result complies with Ref. [20], which proposed that the yield strength of cell wall material has a linear influence on the plateau stress of aluminum foams. Foams can be made from many kinds of materials including metals, plastics, and even ceramics. The properties depend on two kinds of parameters. The first is the intrinsic properties of the cell wall material, and the second is the special distribution of the cell wall material. If the second kind of parameter is somehow unalterable, the modification and refinement of the cell wall material is a feasible way to improve the foam performance.
3.5 Uniaxial compression tests and simulation results
The properties of the raw material and solid material are obtained from experiment while the properties of the cell wall material are still unknown in this work. Therefore, in the following simulation, we substitute the properties of solid material for the properties of cell wall material. Various models based on the actual specimen structure were developed to obtain the plateau stress. The simulated plateau stress was compared with the experimental data to get an understanding of the properties of cell wall material.
The cell size is determined by cross section measurement as Ref. [16] proposed. The cell anisotropy ratio is the transverse cell size over the longitudinal cell size. Subsequently, finite element models were established based on the actual parameters of aluminum foams if we input the cell wall thickness, Kelvin tetrakaidecahedron cell edge length and the anisotropy ratio, which can be calculated or directly obtained from Table 1. The material models are identical for all the cases. The property of solid material is used in the simulation.
Table 1 Comparison between experimental and simulation results of compressive performance of Al foams

The simulation stress-strain curves were obtained and the plateau stress was calculated and compared with experimental data. The experimental results as well as the simulation results are compared in Table 1. Figure 9 shows the comparison of plateau stress between experimental results and simulation results. Although the data are scattered, a clear positive correlation can be seen. The simulation results are higher than the experimental results while the difference between experimental results and simulation results is not regular. Statistically speaking, the experimental results are averagely 36% less than the simulation data, which can be attributed to many factors such as the substitution of solid material for cell wall material. The yield strength of cell wall material is lower than that of solid material, so it is reasonable that the experimental plateau stress is lower that the simulation data.
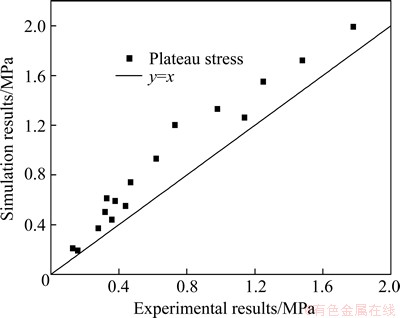
Fig. 9 Plateau stress of nominal stress-strain curve
The relative density of the aluminum foams covers a wide range. Generally speaking, the experimental plateau stress of a typical specimen with the relative density of 0.1 is about 1 MPa. The energy absorption capacity of the aluminum foam is satisfying for the impact of a domestic car at a normal speed. The conversion of kinetic energy into other kinds of energy, mostly heat, must be done while holding the force nearly constant. The aluminum foams are proved to be suitable for that application. The energy is absorbed at the expanse of the deformation of the cell structure including the bending, buckling or the fracture of the cell wall material. It is therefore that the improvement of the cell wall property and the elimination of the defects in the cell wall are beneficial for practical use.
The significant improvement in energy absorption capacity and plateau stress can be obtained by the refinement of cell structure and improvement of cell wall properties. If we can improve the performance of cell wall material to reach the performance of raw material, a giant improvement of plateau stress of aluminum foams can be expected. However, the performance of cell wall material is often much lower than the performance of raw material, so the property improvement of cell wall material is an effective way to improve the plateau stress of aluminum foams. Moreover, in occasions where the cell structure is already refined, the improvement of the property of cell wall material is a promising way to enhance the energy absorption capability of aluminum foams.
4 Conclusions
1) The crush behavior of the cell wall material is brittle compared to the raw material. Therefore, the property of cell wall material is impaired by the defects in the cell wall and the oxide film on the cell wall surface.
2) The true stress-strain curves of raw material and solid material are measured experimentally and used in finite element models. The results show that the plateau stress of aluminum foams exhibits a linear relationship with the yield strength of the cell wall materials.
3) The experimental results are compared with simulation data, which indicates that for an aluminum foam specimen, the property difference between cell wall material and raw material can cause great loss to plateau stress. The property improvement of cell wall material is therefore beneficial for the plateau stress and energy absorption capacity of aluminum foams.
References
[1] SAADATFAR M, MUKHERJEE M, MADADI M,  G E, GARCIA-MORENO F, SCHALLER F M, HUTZLER S, SHEPPARD A P, BANHART J, RAMAMURTY U. Structure and deformation correlation of closed-cell aluminium foam subject to uniaxial compression [J]. Acta Materialia, 2012, 60(8): 3604-3615.
G E, GARCIA-MORENO F, SCHALLER F M, HUTZLER S, SHEPPARD A P, BANHART J, RAMAMURTY U. Structure and deformation correlation of closed-cell aluminium foam subject to uniaxial compression [J]. Acta Materialia, 2012, 60(8): 3604-3615.
[2] PERONI M, SOLOMOS G, PIZZINATO V. Impact behaviour testing of aluminium foam [J]. International Journal of Impact Engineering, 2013, 53: 74-83.
[3] OPPENHEIMER S M, DUNAND D C. Finite element modeling of creep deformation in cellular metals [J]. Acta Materialia, 2007, 55(11): 3825-3834.
[4] MARKAKI A E, CLYNE T W. The effect of cell wall microstructure on the deformation and fracture of aluminium-based foams [J]. Acta Materialia, 2001, 49(9): 1677-1686.
[5] ZHU H X, HOBDELL J R, WINDLE A H. Effects of cell irregularity on the elastic properties of open-cell foams [J]. Acta Materialia, 2000, 48(20): 4893-4900.
[6] SIMONE A E, GIBSON L J. The effects of cell face curvature and corrugations on the stiffness and strength of metallic foams [J]. Acta Materialia, 1998, 46(11): 3929-3935.
[7] SIMONE A E, GIBSON L J. Effects of solid distribution on the stiffness and strength of metallic foams [J]. Acta Materialia, 1998, 46(6): 2139-2150.
[8] MEGUID S A, CHEON S S, EL-ABBASI N. FE modelling of deformation localization in metallic foams [J]. Finite Elements in Analysis and Design, 2002, 38(7): 631-643.
[9] LU Zi-xing, LIU Qiang, HUANG Ji-xiang. Analysis of defects on the compressive behaviors of open-cell metal foams through models using the FEM [J]. Materials Science and Engineering A, 2011, 530: 285-296.
[10] de GIORGI M, CAROFALO A, DATTOMA V, NOBILE R, PALANO F. Aluminium foams structural modelling [J]. Computers and Structures, 2010, 88(1-2): 25-35.
[11] JEENAGER V K, PANCHOLI V. Influence of cell wall microstructure on the energy absorption capability of aluminium foam [J]. Materials & Design, 2014, 56: 454-459.
[12] CAMPANA F, PILONE D. Effect of wall microstructure and morphometric parameters on the crush behaviour of Al alloy foams [J]. Materials Science and Engineering A, 2008, 479(1): 58-64.
[13] JEON I, KATOU K, SONODA T, ASAHINA T, KANG K J. Cell wall mechanical properties of closed-cell Al foam [J]. Mechanics of Materials, 2009, 41(1): 60-73.
[14] JEON I, ASAHINA T, KANG K J, IM S, LU T J. Finite element simulation of the plastic collapse of closed-cell aluminum foams with X-ray computed tomography [J]. Mechanics of Materials, 2010, 42(3): 227-236.
[15] TODA H, OHGAKI T, UESUGI K, KOBAYASHI M, KURODA N, KOBAYASHI T, NIINOMI M, AKAHORI T, MAKII K, ARUGA Y. Quantitative assessment of microstructure and its effects on compression behavior of aluminum foams via high-resolution synchrotron X-ray tomography [J]. Metallurgical and Materials Transactions A, 2006, 37(4): 1211-1219.
[16] FAN Xue-liu, CHEN Xiang, LIU Xing-nan, LI Yan-xiang. Properties of aluminum foam prepared by gas injection method [J]. The Chinese Journal of Nonferrous Metals, 2011, 21(6): 1320-1327. (in Chinese)
[17] MILLER R E. A continuum plasticity model for the constitutive and indentation behaviour of foamed metals [J]. International Journal of Mechanical Sciences, 2000, 42(4): 729-754.
[18] ATTIA M S, MEGUID S A, NOURAEI H. Nonlinear finite element analysis of the crush behaviour of functionally graded foam-filled columns [J]. Finite Elements in Analysis and Design, 2012, 61: 50-59.
[19] SANTOSA S, WIERZBICKI T. Crash behavior of box columns filled with aluminum honeycomb or foam [J]. Computers and Structures, 1998, 68(4): 343-367.
[20] ASHBY M F, GIBSON L J. Cellular Solids: Structure and Properties [M]. Cambridge, UK: Press Syndicate of the University of Cambridge, 1997: 183-231.
袁建宇1,李言祥1, 2
1. 清华大学 材料学院,北京 100084;2. 清华大学 先进成形制造教育部重点实验室,北京100084
摘 要:针对吹气法制备的高孔隙率闭孔泡沫铝,通过实验和有限元分析研究泡壁材料性能对其压缩性能的影响。向添加陶瓷颗粒的A356合金熔体中吹气发泡制备实验样品并进行单向压缩。通过光学显微镜和扫描电镜观察泡壁的微观组织和断口组织。结果表明,泡壁中存在的颗粒团聚、孔洞等缺陷和氧化膜削弱了其性能,因此,泡沫材料的性能与原材料性能有很大差别。基于原材料性能和实体材料性能的实验结果,对泡沫铝理想三维结构进行有限元分析。材料的平台应力与泡沫材料的屈服强度成正比。有限元模拟结果稍高于实验结果,其部分原因是将实体材料性能看做泡壁材料性能导致的。
关键词:泡沫铝;泡沫材料性能;单向压缩性能;有限元分析
(Edited by Yun-bin HE)
Foundation item: Project (2013DFR50330) supported by the International Cooperation Project of Science and Technology Ministry of China
Corresponding author: Yan-xiang LI; Tel: +86-10-62773640; E-mail: yanxiang@tsinghua.edu.cn
DOI: 10.1016/S1003-6326(15)63766-9

