Flow stress behavior and constitutive modeling of 20MnNiMo low carbon alloy
来源期刊:中南大学学报(英文版)2016年第8期
论文作者:王梦寒 王根田 王瑞
文章页码:1863 - 1872
Key words:pressure vessel steel; flow stress behavior; constitutive model; Arrhenius model; Johnson-Cook model
Abstract: The hot deformation behavior of 20MnNiMo low carbon alloy was investigated by isothermal compression tests over wide ranges of temperature (1223-1523 K) and strain rate (0.01-10 s-1). According to the experimental true stress-true strain data, the constitutive relationships were comparatively studied based on the Arrhenius-type model, Johnson-Cook (JC) model and artificial neural network (ANN), respectively. Furthermore, the predictability of the developed models was evaluated by calculating the correlation coefficient (R) and mean absolute relative error (AARE). The results indicate that the flow stress behavior of 20MnNiMo low carbon alloy is significantly influenced by the strain rate and deformation temperature. Compared with the Arrhenius-type model and Johnson-Cook (JC) model, the ANN model is more efficient and has much higher accuracy in describing the flow stress behavior during hot compressing deformation for 20MnNiMo low carbon alloy.
J. Cent. South Univ. (2016) 23: 1863-1872
DOI: 10.1007/s11771-016-3241-7
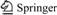
WANG Meng-han(王梦寒), WANG Gen-tian(王根田), WANG Rui(王瑞)
School of Materials Science and Engineering, Chongqing University, Chongqing 400044, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: The hot deformation behavior of 20MnNiMo low carbon alloy was investigated by isothermal compression tests over wide ranges of temperature (1223-1523 K) and strain rate (0.01-10 s-1). According to the experimental true stress-true strain data, the constitutive relationships were comparatively studied based on the Arrhenius-type model, Johnson-Cook (JC) model and artificial neural network (ANN), respectively. Furthermore, the predictability of the developed models was evaluated by calculating the correlation coefficient (R) and mean absolute relative error (AARE). The results indicate that the flow stress behavior of 20MnNiMo low carbon alloy is significantly influenced by the strain rate and deformation temperature. Compared with the Arrhenius-type model and Johnson-Cook (JC) model, the ANN model is more efficient and has much higher accuracy in describing the flow stress behavior during hot compressing deformation for 20MnNiMo low carbon alloy.
Key words: pressure vessel steel; flow stress behavior; constitutive model; Arrhenius model; Johnson-Cook model
1 Introduction
From the industrial perspective, hot deformation for metals or alloys has been highly performed in the manufacture of converting cast ingots into wrought products with desired dimensional accuracy and required properties, such as forging, rolling and extrusion [1]. While, the flow stress behavior during hot deformation is usually complicated, since the work hardening, dynamic softening, dynamic recovery (DRV) and dynamic recrystallization (DRX) are significantly influenced by processing parameters, and finally affect the mechanical properties [2]. Thus, the identification of the relationship between flow stress and processing parameters is very crucial for designing the hot deformation process. On the other hand, the finite element method (FEM) simulations which include the material constants and constitutive equations gradually play an effective role in the industrial production [3-4]. Consequently, the constitutive model and its predictability have become an interesting research hotspot in recent years [5-9].
In fact, the constitutive model is usually composed of one or more mathematical equations which can be used to describe the correlation between flow stress behavior and strain, strain rate and temperature under different deformation conditions. During hot deformation process of metallic materials, it can be applied to determine the deformation load, to establish the hot processing map and to investigate the dynamic recrystallization kinetics [10]. At present, there are three typical types of constitutive models to depict the flow stress behavior for metals and alloys: analytical [11], phenomenological [12] and empirical [13]. The phenomenological model is the most commonly used because of the less material constants involved in regression analysis, especially the Arrhenius and Johnson-Cook model. Lately, an artificial intelligent method called artificial neural network (ANN) was proposed to develop the constitutive relationship [14-15]. ANN model is good at analyzing non-linear situations and unknown data prediction, thus it has been applied in many aspects of materials science including the prediction of flow stress behavior [16-17] and generation of processing maps for hot deformation process [18].
20MnNiMo low carbon alloy (ASME SA508 class 3) is widely applied in the manufacture of nuclear reactor pressure vessels (RPV), compressors, and steam generators of nuclear power plants due to its moderate strength, superior toughness and high weldability [19]. Up to now, considerable investigations have been conducted on the fracture toughness [20], welding performance [21] and the effect of alloy elements on the mechanical properties [22]. While, there is still a lack of systematic research on the constitutive modeling of this type of alloy. For the aim of conducting relatively reasonable finite element method (FEM) analysis under complex processing conditions of the studied material and cutting down the production cost,it is highly necessary to establish accurate constitutive models by investigating the flow stress behavior for this alloy.
For this purpose, in the current work, the flow stress behavior of 20MnNiMo low carbon alloy is investigated through conducting hot compression tests at different deformation temperatures and strain rates. Then, the experimental data are employed to develop Arrhenius-type model, Johnson-Cook model and artificial neural network (ANN) model, respectively. Finally, the validation of the established models is evaluated on the basis of standard statistical parameters, such as the correlation coefficient (R) and the mean absolute relative error (MARE).
2 Material and experimental procedure
The material employed in this work was provided in the form of bar by casting (30 mm in diameter and 200 mm in height). Its composition is as follows (mass fraction): 0.20%C, 0.16%Si, 1.39%Mn, 0.80%Ni, 0.50%Mo, 0.15%Cr, 0.003%S, 0.005%P, 0.005%V, 0.04%Cu, 0.02%Al and Fe bal. The processing of homogenizing annealing heat treatment was conducted in a high temperature vacuum furnace at 1473 K for 16 h and then the homogenized ingot was scalped to the diameter of 8 mm and the height of 12 mm with cylinder axes parallel to the axial line direction of the bar. Before each testing, all specimens were heated to the deformation temperature at a heating rate of 20 K/s and held for 3 min to obtain uniform temperature. Hot compression tests were conducted on THE RMECMASTOR-Z in the temperature ranges of 1223-1523 K (an interval of 100 K) and strain rate of 0.01, 0.1, 1 and 10 s-1. Finally, all the compressed samples were water quenched immediately.
3 Results and discussion
3.1 Flow behavior
Based on thermal compression data, the flow stress-strain curves at various temperatures and strain rates are depicted in Fig. 1. As can be seen, the deformation temperature and strain rate has a distinct effect on the flow behavior of 20MnNiMo low carbon alloy. Just as many alloys [10, 23-24], for a certain temperature, the flow stress increases with the increase of strain rate. For a certain strain rate, the flow stress decreases with the increase of temperature. This phenomenon can be attributed to the fact that low temperature and high strain rate cannot provide sufficient energy and time for dislocation accumulation and annihilation. As a result, much higher flow stress is imposed to continue the deformation process. In the initial stage of hot compression, all flow curves increase promptly due to the work hardening. After that, the flow stress increases slightly until a peak stress (0.01 and 1.0 s-1 at 1223, 1323, 1423 and 1523 K) or directly keeps dynamic balance (1 and 10 s-1 at 1223, 1323, 1423 and 1523 K). For the former, the flow stress also reaches a balance stage with the increase of true strain. This is mainly because the softening caused by dynamic recrystallization (DRX) and dynamic recovery (DRV) finally counteracts the work hardening effect. In this work, the DRX tends to dominate softening mechanism under different compression tests, since the studied material yields low stacking fault energy.
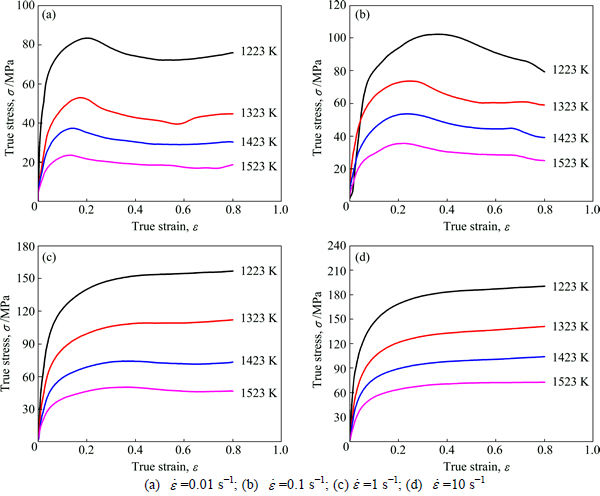
Fig. 1 True stress-stain curves of 20MnNiMo alloy under different temperatures and strain rates:
3.2 Arrhenius-type model
3.2.1 Classic Arrhenius model
It is widely known that temperature and strain rate are the main influencing factors during the hot deformation. As shown in Eq. (1), the effects of them can be represented by the Zener–Hollomon parameter [25]. And the dependence of flow stress on the deformation temperature and strain rate during hot deformation can be given by the classic Arrhenius model (Eq. (2)):
 (1)
(1)
 (2)
(2)
 , if ασ<0.8 (3)
, if ασ<0.8 (3)
F(σ)=A2exp(βσ), if ασ>1.2 (4)
F(σ)=A[sinh(ασp)]nexp[Q/(RT), for all σ (5)
where σ is the flow stress for a given true strain; Q is the thermal activation energy; R is the gas constant (8.31 J·mol-1·K-1); T is the thermodynamic temperature; A1, A2, A, n1, n, β and α (β/n1) are material constants.
In order to obtain the material constants and thermal energy Q, the natural logarithms based on Eqs. (3)-(5) are derived:
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
In this work, the flow stress at true strain of 0.4 was used for above linear regression analysis to determine the hot deformation behavior of the material. Based on the linear relationships (shown in Fig. 2) between  and lnσ, σ, ln[sinh(ασ)], respectively, and the linear relationships of ln[sinh(ασ)]-1/T, the value of material constants and Q can be calculated as follows: n1=5.98, n=4.2177, β=0.0905, A=6.8×1012, α=β/n1=0.01515 MPa-1 and Q=360.445 kJ/mol.
and lnσ, σ, ln[sinh(ασ)], respectively, and the linear relationships of ln[sinh(ασ)]-1/T, the value of material constants and Q can be calculated as follows: n1=5.98, n=4.2177, β=0.0905, A=6.8×1012, α=β/n1=0.01515 MPa-1 and Q=360.445 kJ/mol.
Fig. 2 Linear relationships of  -lnσ (a),
-lnσ (a),  (b),
(b),  -ln[sinh(ασ)] (c) and ln[sinh(ασ)]-1/T (d)
-ln[sinh(ασ)] (c) and ln[sinh(ασ)]-1/T (d)
Combining Eqs. (1) and (2), the flow stress can be described by the Zener–Holloman parameter as
 (10)
(10)
On the basis of the above experimental data and results, the constitutive equation can be expressed as
 =6.8×1012[sinh(0.01515σ)]4.2177exp(-360.445/(RT)) (11)
=6.8×1012[sinh(0.01515σ)]4.2177exp(-360.445/(RT)) (11)
Moreover, the flow stress can be written as a function of Zener-Hollomon, according to Eq. (10), which is given as
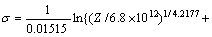
 (12)
(12)
where  .
.
3.2.2 Strain compensation Arrhenius model
It is well known that the flow stress usually varies with true strain, especially when the dynamic recrystallization (DRX) and dynamic recovery (DRV) occur. As a result, the classic Arrhenius model might be inadequate to depict the flow behavior. For the modifiedArrhenius model, the influence of true strain on the hot deformation behavior of alloy is taken into account on the basis of classic Arrhenius model so as to provide more precise prediction on the flow behavior [26-27]. The material constants of Q, α, n and lnA at different true strains (from 0.1 to 0.8, with the interval of 0.05) are determined according to the same method in section 3.2.1, and the values of these material constants with different strains are plotted in Fig. 3.
As can be seen, both the material constants of Q, n and A decrease with the increase of true strains. However, the other material constant α firstly decreases with the increase of true strains and then approximately trends to be stable. At present, it is widely accepted that Q, α, n and lnA for a specified alloy are considered to be strain dependent [7] and a polynomial fitting can be applied to describe the relationship between them and the strain, as expressed in the following equation:
 (13)
(13)
The power (m) of the polynomial is varied from one to nine. In this work, a 6th-order polynomial fit is chosen on the basis of the analysis of correlation and generalization. And the correlation coefficients of them are 0.995, 0.990, 0.992 and 0.989, respectively. The detailed values of polynomial fitting coefficients of Q, α, n, and lnA are given in Table 1. As a result, the Arrhenius model is modified by considering the effect of true strain:
 (14)
(14)
Table 1 Coefficients of polynomial fitting curves for material coefficients
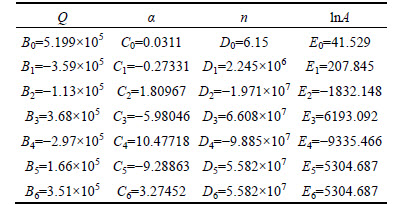
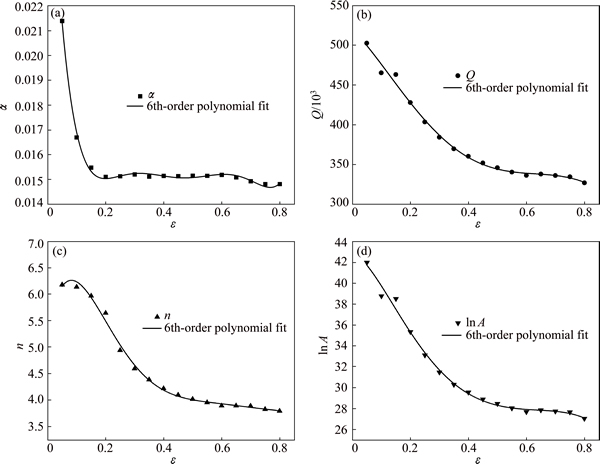
Fig. 3 Variations of α (a), Q (b), n (c) and lnA (d) with true strain
3.3 Johnson-Cook (JC) model
In 1983, JOHNSON and COOK developed an empirical model for alloys over a wide range of temperatures and strains in which the flow stress was considered to be a function of deformation temperature, true strain and strain rate:
 (15)
(15)
where σ is flow stress; ε is the strain; A is the yield stress at reference temperature and strain rate; B is the strain hardening coefficient; n is the strain hardening exponent; and C and m are the material constants which represent the coefficient of strain rate hardening and thermal softening exponent, respectively; is the dimensionless strain rate which could be express as
is the dimensionless strain rate which could be express as  , where
, where  is the strain rate and
is the strain rate and  is the reference strain rate; T* is the homologous temperature and can be expressed as
is the reference strain rate; T* is the homologous temperature and can be expressed as
T*=(T-Tr)/(Tm-Tr) (16)
where T is the deformation temperature; Tm is the melting temperature of the investigated material (1795 K) and Tr is the reference temperature. In Eq. (15), (A+Bεn), and (1-T*m) are used to describe the work hardening effect, strain rate effect and temperature effect, respectively [15].
and (1-T*m) are used to describe the work hardening effect, strain rate effect and temperature effect, respectively [15].
In order to investigate the hot deformation behavior of 20MnNiMo low carbon alloy, 1223 K and 0.01 s-1 (the minimum deformation temperature and minimum strain rate) were taken as the reference temperature and strain rate in the Johnson-Cook (JC) model, respectively. In the equation, A is the yield stress (10.68 MPa) at the reference temperature and reference strain rate which is equal to the value of stress at true strain rate of 0.002 [28].
When the deformation temperature is 1223 K and strain rate is 0.01 s-1, Eq. (15) can be expressed as follows:
σ=A+Bεn (17)
Taking the logarithm of both sides of Eq. (17) gives
ln(σ-A)=nlnε+lnB (18)
The value of n and B can be obtained as 0.18 MPa and 98.5 from the slope and intercept of the fitting line in the ln(σ-A)=nlnε plot in Fig. 4, respectively.
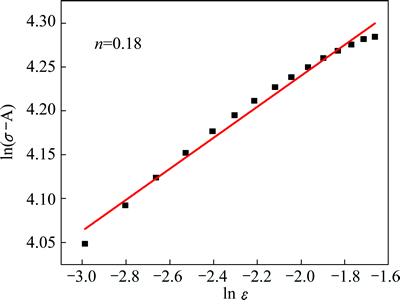
Fig. 4 Linear relationship between ln(σ-A) and ln ε
When the deformation temperature is 1223 K, the reference temperature T*=0, and Eq. (15) can be expressed as follows:
 (19)
(19)
The value of C can be obtained as 0.168 from the slope of the fitting line between σ/(A+Bεn) and in Fig. 5.
in Fig. 5.
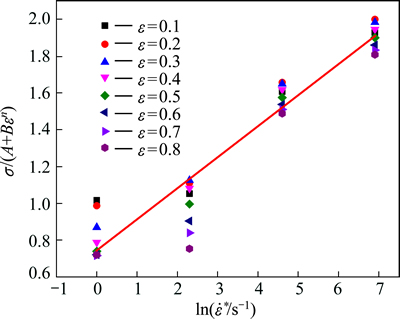
Fig. 5 Linear relationships between σ/(A/Bεn) and 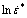
When the strain rate is 0.01 s-1, the dimensionless strain rate  = 0, and Eq. (15) gives
= 0, and Eq. (15) gives
 (20)
(20)
The value of exponent m can be obtained as 0.427 from the slope of linear fit to ln{1-σ/(A+Bεn)} vs  curve in Fig. 6.
curve in Fig. 6.
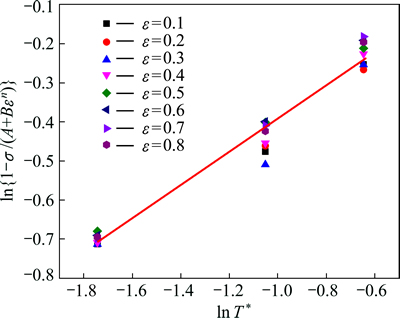
Fig. 6 Linear relationships between ln{1-σ/(A+Bεn)} and T*
Finally, the JC model for the studied 20MnNiMo low alloy can be expressed by
 (21)
(21)
3.4 Artificial neural network (ANN) model
Artificial neural network is basically a data driven black box linking the input data to output data using a special set of nonlinear functions [13]. Generally, a typical neural network includes one input layer, one or more hidden layers and one output layer. And its establishment is mainly composed of four stages: (1) determine the input/output parameters based on the experimental data; (2) analyze the collected data; (3) train the ANN and test the trained ANN; (4) estimate the capability of the established ANN. Up to now, ANN has been widely applied to model the flow behavior of various kinds of steels [6], aluminums [8] and titanium alloys [9, 24]. In this work, a three-layer ANN model was established to evaluate the flow behavior of the 20MnNiMo low alloy steel, and the true strain (ε), strain rate ( ), deformation temperature (T) constitute the input parameters, and the flow stress (σ) is determined as the output. The main schematic of the ANN model is shown in Fig. 7.
), deformation temperature (T) constitute the input parameters, and the flow stress (σ) is determined as the output. The main schematic of the ANN model is shown in Fig. 7.
The flow stress data (from 0.1 to 0.8, with an interval of 0.05, 240 data points) are divided into three parts randomly: training part (80% of the total data points), which is used for updating the weights and minimizing the deviation; validation part (15% of the total data points), which is used for measuring generation ability of the model and checking whether over fitting or not; testing part (5% of the total data points), which is set as an independent database for measuring performance of the model after training. The Levenberg-Marquardt (LM) algorithm is adopted for training ANN on account of its fast convergence in training [12]. On the other hand, in order to guarantee that each parameter ( , ε, T, σ) is trained and tested within the same range, all the data are conducted by normalized processing based on Eq. (22). In the current work, the target for mean absolute error (MAE) of training is set as 0.001 and the network training will not stopped until the target for MAE is achieved:
, ε, T, σ) is trained and tested within the same range, all the data are conducted by normalized processing based on Eq. (22). In the current work, the target for mean absolute error (MAE) of training is set as 0.001 and the network training will not stopped until the target for MAE is achieved:
 (22)
(22)
where X is the original flow stress data; X′ is the normalized flow stress data; and Xmax and Xmin are the maximum and minimum flow stress data, respectively.
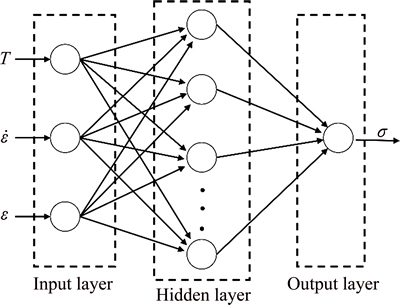
Fig. 7 Schematic illustration of ANN structure
3.5 Model validation
In this section, in order to verify the predictability of the developed model, the correlation coefficient (R), the relative error and the mean absolute relative error (MARE, E) are calculated based on the following expressions:
 (23)
(23)
 (24)
(24)
where Ei is the experimental flow stress and Pi is the predicted flow stress calculated from the developed models;  and
and  are the mean values of experimental and predicted flow stress data, respectively; N is the total number of data applied in this work; R is used to show the linear relationship between the predicted data and experimental data.
are the mean values of experimental and predicted flow stress data, respectively; N is the total number of data applied in this work; R is used to show the linear relationship between the predicted data and experimental data.
The correlations between the experimental data and the predicted data obtained from modified Arrhenius model and JC model are shown in Fig. 8 (the solid line represents the best match between the experimental and predicted values). As can be seen, the correlation coefficients (R) obtained from modified Arrhenius model and JC model are 0.9923 and 0.9557, respectively. And the value of MARE calculated from JC model is 16.8%, which is higher than that calculated from improved Arrhenius modified (6.51%). The comparison between the experimental and predicted flow stress values calculated by modified Arrhenius model and JC model are plotted in Fig. 9 and 10, respectively. It can be clearly seen that there exist some deviation between the experimental and predicted values, especially for the JC model. The reason should be that JC model cannot describe both work hardening and softening behavior simultaneously [29], as the thermal softening, and strain hardening are assumed to be independent in the JC model [30]. On the other hand, the flow behavior of the studied alloy and related influence factors are highly nonlinear under various true strains, strain rates and temperatures.
Fig. 8 Correlations between experimental and predicted flow stress data at different conditions:
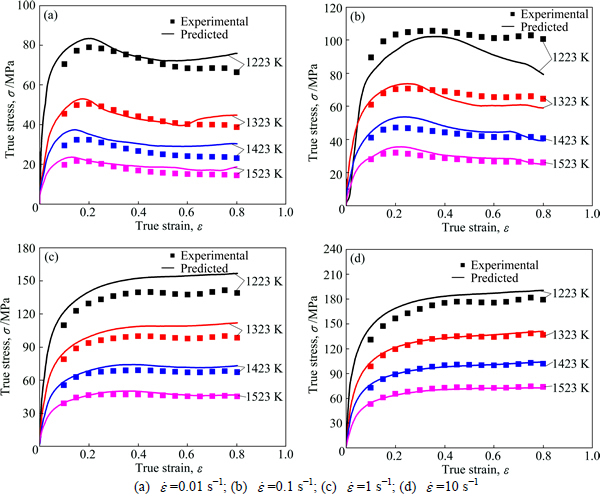
Fig. 9 Comparison between predicted and experimental flow stress curves by modified Arrhenius model under different strain rates:
As for the accuracy of the developed ANN model, its correlation performance and absolute error between the experimental and predicted values are shown in Fig. 11. It can be seen that most of the data points fall on the solid line, and the correlation coefficients (R) is 0.9996, the value of MARE is 1.32% (Fig. 11(a)). And about 96% of the absolute errors are shown to be less than 3 MPa within the whole predicted flow stress data (Fig. 11(b)). Obviously, the predicted flow stress values show much better agreement with the experimental data than Arrhenius-type and JC model. At last, the measured true stress–true strain curves and predicted values calculated by ANN model are plotted and compared in Fig. 12. Apparently, the best agreement between experimental and predicted values can be observed in ANN model.
4 Conclusions
In this work, the flow behavior and three constitutive models (Arrhenius-type, Johnson-Cook model and ANN model) of 20MnNiMo low alloy were investigated and established, respectively, by isothermal compression tests in temperature ranges of 1223-1523 K and strain rate of 0.01-10 s-1. The following conclusions can be drawn.
1) The flow stress of 20MnNiMo low alloy increases with the increase of strain rate, and decreases with the increase of deformation temperature. For a certain temperature and strain, the flow stress firstly increases promptly to a peak value and finally reaches a dynamic balance stage with the increase of true strain.
2) In the modified Arrhenius model, the values of Q, n, A and α are found to be functions of true strain. The thermal activation energy (Q), stress exponent (n) and material constant (A) decrease with the increase of true strains. However, the other material constant α firstly decreases with the increase of true strains and then approximately trends to be stable.
3) The predictability of modified Arrhenius model and JC model for the flow behavior of 20MnNiMo alloy are inadequate, especially for the JC model. The correlation coefficient (R) and the mean absolute relative error (MARE) from the established ANN model are 0.9996 and 1.32%, respectively. Synthetically, the ANN model has much better efficiency and higher accuracy in predicting the flow behavior of 20MnNiMo alloy.

Fig. 10 Comparison between predicted and experimental flow stress curves by Johnson-Cook model under different strain rates:
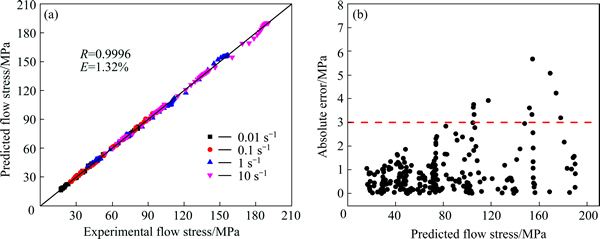
Fig. 11 Correlations (a) and absolute error (b) between experimental and predicted flow stress data
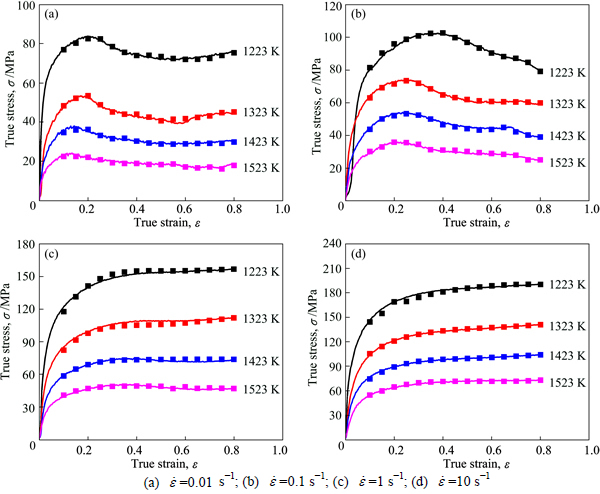
Fig. 12 Comparison between predicted and experimental flow stress curves by ANN model under different strain rates:
References
[1] LIANG Wen-jie, PAN Qing-lin, HE Yun-bin, LI Yun-chun, ZHANG Xiao-gang. Flow stress behavior of Al-Cu-Li-Zr alloy containing Sc during hot compression deformation [J]. Journal of Central South University of Technology, 2008, 15(3): 289-294.
[2] LI Bo, PAN Qing-lin, LI Chen, ZHANG Zhi-ye, YIN Zhi-min. Hot compressive deformation behavior and constitutive relationship of Al-Zn-Mg-Zr alloy with trace amounts of Sc [J]. Journal of Central South University, 2013, 20(11): 2939-2946.
[3] JI Hong-chao, LIU Jin-ping, WANG Bao-yu, ZHANG Zheng-rong, ZHANG Tao, HU Zheng-huan. Numerical analysis and experiment on cross wedge rolling and forging for engine valves [J]. J Mater Process Tech, 2015, 221: 233-242.
[4] LI Xu, WANG Hong-yu, DING Jing-guo, LI Xu, WANG Hong-yu, DING Jing-guo, XU Jiu-jing, ZHANG Dian-hua. Analysis and prediction of fishtail during V-H hot rolling process [J]. Journal of Central South University, 2015, 22(4): 1184-1190.
[5] SAREBANZADEH M, MAHMUDI R, ROUMINA R. Constitutive analysis and processing map of an extruded Mg-3Gd-1Zn alloy under hot shear deformation [J]. Mater Sci Eng A, 2015, 18: 155-161.
[6] WEI Feng, FU You-heng. High temperature deformation behavior and constitutive modeling for 20CrMnTiH steel [J]. Mater Des, 2014, 57: 465-471.
[7] LI Li, LI Hui-zhong, LIANG Xiao-peng, HUANG Lan, HONG Tao. Flow stress behavior of high purity Al-Cu-Mg alloy and microstructure evolution [J]. Journal of Central South University, 2015, 22(3): 815-820.
[8] LIN Yong-cheng, DING Yi, CHEN Ming-song, DENG Jiao. A new phenomenological constitutive model for hot tensile deformation behaviors of a typical Al-Cu-Mg alloy [J]. Mater Des, 2013, 52: 118-127.
[9] ZENG Zhi-peng, JONSSON S, ZHANG Yan-shu. Constitutive equations for pure titanium at elevated temperatures [J]. Mater Sci Eng A, 2009, 505: 116-119.
[10] LI Bo, PAN Qing-lin, YIN Zhi-min. Microstructural evolution and constitutive relationship of Al-Zn-Mg alloy containing small amount of Sc and Zr during hot deformation based on Arrhenius-type and artificial neural network models [J]. J Alloy Compd, 2014, 584: 406-416.
[11] LUO Jiao, LI Miao-quan, LI Xiao-li, SHI Yan-pei. Constitutive model for high temperature deformation of titanium alloys using internal state variables [J]. Mech Mater, 2010, 42: 157-165.
[12] HAN Ying, QIAO Guan-juan, SUN Jia-peng, ZOU De-ning. A comparative study on constitutive relationship of as-cast 904L austenitic stainless steel during hot deformation based on Arrhenius-type and artificial neural network models [J]. Comput Mater Sci, 2013, 67: 93-103.
[13] ZHAO Jing-wei, HUA Ding, ZHAO Wen-juan, HUANG Ming-li, WEI Dong-bin, JIANG Zheng-yi. Modelling of the hot deformation behaviour of a titanium alloy using constitutive equations and artificial neural network [J]. Comput Mater Sci, 2014, 92: 47-56.
[14] LIN Yong-cheng, ZHANG Jun, ZHONG Jue. Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel, Comput [J]. Mater Sci, 2008, 43: 752-758.
[15] LIN Yong-cheng, CHEN Xiao-min. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Mater Des, 2011, 32: 1733-1759.
[16] SUN Yu, ZENG Wei-dong, HAN Yuan-fei, MA Xiong, ZHAO Yong-qing, GUO Ping, WANG Gui, DARGUSCH M S. Determination of the influence of processing parameters on the mechanical properties of the Ti-6Al-4V alloy using an artificial neural network [J]. Comput Mater Sci, 2012, 60: 239-244.
[17] GUPTA A K, SINGH S K, REDDY S, HARIHARAN G. Prediction of flow stress in dynamic strain aging regime of austenitic stainless steel 316 using artificial neural network [J]. Mater Des, 2012, 35: 589-595.
[18] MANDAL S, SIVAPRASAD P V, VENUGOPAL S, MURTHY K P N, RAJ B. Artificial neural network modeling of composition process property correlations in austenitic stainless steels [J]. Mat Sci Eng A, 2008, 485: 571-580.
[19] WANG Meng-han, LI Yu-feng, WANG Wen-hao, ZHOU Jie, AKIHIKO C. Quantitative analysis of work hardening and dynamic softening behavior of low carbon alloy steel based on the flow stress [J]. Mater Des, 2013, 45: 384-392.
[20] KIM M C, PARK S G, LEE K H, LEE B S. Comparison of fracture properties in SA508 Gr.3 and Gr.4N high strength low alloy steels for advanced pressure vessel materials [J]. Inter J Pres Ves Pip, 2015, 131: 60-66.
[21] MING Hong-liang, ZHANG Zhi-ming, WANG Jian-qiu, HAN En-hou, KE Wei. Microstructural characterization of an SA508-309L/308L-316L domestic dissimilar metal welded safe end joint [J]. Mater Charact, 2014, 97: 101-115.
[22] LEE K H, KIM M C, YANG W J, LEE B S. Evaluation of microstructural parameters controlling cleavage fracture [J]. Mater Sci Eng A, 2013, 565: 158-164.
[23] ZHANG Chi, ZHANG Li-wen, SHEN Wei-fei, LI Meng-fei, GU Sen-dong. Characterization of hot deformation behavior of Hastelloy C-276 using constitutive equation and processing map [J]. J Mater Eng Perform, 2014, 24: 149-157.
[24] CAI Jun, WANG Kuai-she, ZHAI Peng, LI Fu-guo, YANG Jie. A modified Johnson-cook constitutive equation to predict hot deformation behavior of Ti-6Al-4V alloy [J]. J Mater Eng Perform, 2014, 24: 32-44.
[25] ZENER C, HOLLOMON J. Effect of strain rate upon plastic flow of steel [J]. J Appl Phys, 1944, 15: 22-32.
[26] LIN Yong-cheng, CHEN Ming-song, ZHONG Jue. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel [J]. Computational Materials Science, 2008, 42: 470-477.
[27] SPIGARELLI S, EL MEHTEDI M. A new constitutive model for the plastic flow of metals at elevated temperatures [J]. J Mater Eng Perform, 2013, 23: 658-665.
[28] ABBASI-BANI A, ZAREI-HANZAKI A, PISHBIN M H, HAGHDADI N. A comparative study on the capability of Johnson-Cook and Arrhenius-type constitutive equations to describe the flow behavior of Mg-6Al-1Zn alloy [J]. Mech Mater, 2014, 71: 52-61.
[29] CHEN Liang, ZHAO Guo-qun, YU Jun-quan. Hot deformation behavior and constitutive modeling of homogenized 6026 aluminum alloy [J]. Mater Des, 2015, 74: 25-35.
[30] LIN Yong-cheng, LI Qi-fei, XIA Yu-chi, LI Lei-ting. A phenomenological constitutive model for high temperature flow stress prediction of Al-Cu-Mg alloy [J]. Mater Sci Eng A, 2012, 534: 654-662.
(Edited by YANG Bing)
Foundation item: Project(CDJZR14130006) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2015-07-28; Accepted date: 2015-12-04
Corresponding author: WANG Meng-han, Associate Professor, PhD; Tel: +86-23-65111493; E-mail: cquwmh@163.com

