文章编号：1004-0609(2014)01-0104-11

压块对H96矩形管绕弯成形回弹与截面变形的作用

朱英霞，刘郁丽，杨  合，李海平

(西北工业大学 凝固技术国家重点实验室 材料学院，西安 710072)

摘  要：为了控制矩形管绕弯成形的回弹和截面变形，建立考虑压块力、速度加载条件的回弹和截面变形有限元预测模型，并对其可靠性进行实验验证。基于所建模型研究压块的摩擦因数、夹持压力和助推速度对H96矩形管回弹与截面变形的影响规律。结果表明：摩擦因数和夹持压力越大，回弹角和横截面高度变形越小。但压块对横、纵截面畸变的作用完全相反；芯头支撑区域内助推速度的变化能够影响回弹量，且不会加剧截面变形。提出变助推速度的压块边界条件组合方案，实现了弯曲角度小于90°和大于等于90°弯管的回弹量分别降低55.31%和36.45%，60°弯管的高度变形量平均降低1.79%，90°和120°弯管的高度变形量最大分别降低5.98%和6.35%。

关键词：绕弯成形；H96矩形管；回弹；截面变形；工艺参数；有限元模拟

中图分类号：TG386　　     文献标志码：A

Impact of pressure die on springback and section deformation of rotary-draw bending of rectangular H96 tube

ZHU Ying-xia, LIU Yu-li, YANG He, LI Hai-ping

(State Key Laboratory of Solidification Processing, School of Materials Science and Engineering,

Northwestern Polytechnical University, Xi’an 710072, China)

Abstract: In order to control springback and section deformation of rotary-draw bending of rectangular tube, the finite element model for springback and sectional deformation prediction, which considers the loading and velocity conditions of pressure die, was established and verified by experiment. Based on the model, the impact of friction coefficient, pressure and boosting velocity of pressure die on springback and section deformation of H96 rectangular tube was investigated. The results show that the larger the friction coefficient and the clamping pressure are, the smaller the springback angle and the cross-section height deformation are. However, the impacts of pressure die on deformations of cross-section and longitudinal-section are completely opposite. The change of boosting velocity within core-filled area can influence the springback amount, while not exacerbate section deformation at the same time. Then, the combinations of pressure die boundary conditions of variable boosting speed were proposed. And by which, it is realized that springback angles are decreased by 55.31% and 36.45%, respectively, for bent tubes smaller than 90° or no less than 90°. The cross-section height deformations are reduced by 1.79% for 60° tube on average, and 5.98% and 6.35%, respectively, for 90° tube and 120° tube at most.

Key words: rotary-draw bending; rectangular H96 tube; springback; section deformation; process parameters; finite element simulation

矩形管在绕弯过程中，其前端被夹块夹持，绕弯曲模一起运动，后端夹持于压块和防皱块之间，受到压块向前的助推作用。压块的载荷边界条件和速度边界条件不仅直接影响矩形管的横、纵截面形状和尺寸的变化，而且还直接影响弯曲过程管坯的切向应力，进而影响管件卸载后的回弹。而回弹和截面变形是影响矩形管绕弯成形质量的关键因素，二者都不可避免且相互间存在耦合作用。因此，研究压块的载荷边界条件和速度边界条件对回弹和截面变形的作用，进而实现对矩形管绕弯过程截面变形和回弹的有效控制，对实现矩形管绕弯精确成形具有重要的理论意义和实用价值。

目前，关于弯曲成形的截面畸变和回弹控制的研究很多。合理的工艺参数或成形条件是实现回弹与截面变形控制的重要途径^[1-4]。如LI等^[3]研究了如何利用由压块和助推块组成的助推装置降低圆管的截面 变形，然而，研究中没有考虑压块的力的边界条件。LI等^[4]和ZHAO等^[5]发现，增加芯头个数以及减小芯头与管坯间隙可以降低圆管截面的变形。然而，针对矩形管绕弯成形，以芯模为代表的模具的工艺参数可调控性差，如在实际生产中由于芯模的磨损，最大化减小芯模与管坯间的间隙也难达到理想程度，且芯头个数的增加会极大地增加抽芯的困难，导致管子的壁厚过度减薄。此外，吴建军等^[6-7]通过等曲率弯曲试验研究，采用模具型面回弹补偿法对空间绕弯圆管的回弹进行了补偿。LIU等^[8]和KATAYAMA等^[9]采用响应面和遗传算法对板料弯曲模进行回弹补偿。然而，模具型面回弹补偿法成本较高且较复杂，CLAUSEN等^[10]、MILLER等^[11]和CORONA^[12]研究加载路径、摩擦和拉压力对矩形管拉弯截面变形和回弹的影响规律，目的在于通过优化成形过程将截面畸变和回弹减少到最小。ZHU等^[13]也从轴向拉伸力和摩擦接触条件方向出发，研究如何减小矩形管拉弯回弹。文献[10-13]都是针对矩形管拉弯过程回弹控制的研究，且没有考虑回弹和截面变形之间的耦合作用。上述研究单方面以如何利用工艺参数控制截面变形或回弹为研究对象，忽视了工艺参数对这二者的影响。ZHU等^[14]通过研究发现，较之夹块的夹持力、防皱块-弯曲模与管坯间摩擦因数和芯头个数，压块的夹持力和助推速度不仅对矩形管的回弹影响最显著，而且对截面变形有重要作用。

因此，本文作者基于ABAQUS/Explicit建立可靠的H96矩形管绕弯回弹全程有限元模型，利用该模型分别研究压块的摩擦因数、夹持压力和助推速度对回弹和截面变形的影响规律，并进一步研究如何综合利用压块的边界条件实现回弹和截面变形的双重控制。

1  回弹角和截面变形的定义

1.1  回弹角的定义

采用回弹角表示回弹量的大小，假设矩形管的弯曲角度为θ，回弹后变为θ′，则回弹角可由公式(1)计算，

Δθ=θ-θ′                                   (1)

1.2  截面变形的定义

矩形管绕弯成形结束后，既有横截面变形又有纵截面变形。横截面的变形如图1(a)所示，表现为内、外腹板的塌陷和侧壁的鼓起，即既有高度方向的变形，又有宽度方向的变形。宽度方向变形较小，最大变形出现在内、外腹板截面的对称线上，因此，为了简化研究，只研究截面对称线上高度方向的变形Δh_i，如式(2)所示。

                  (2)

式中：h是矩形管未变形前的截面高度；i代表沿弯曲方向的节点，x_i、y_i和、分别是i节点内、外腹板对称线上的坐标，如图1(b)所示。

图1 矩形管绕弯过程横、纵截面的变形

Fig. 1  Deformation of cross-section and longitudinal-section of rectangular tube

纵截面的变形表现为由压块的助推作用造成的内外腹板的弯曲半径的变化，即椭圆化，其中内、外腹板对称线上截面的椭圆化最严重，如图1(b)所示。内、外腹板对称纵截面的椭圆变形ΔL_i、Δl_i分别按照公式(3)和(4)计算，

                            (3)

                            (4)

式中：R和r分别为内、外腹板不发生椭圆化的标准弯曲半径。

为了分析截面高度变形量和内外腹板椭圆化程度在绕弯进程中的变化，选取沿弯曲方向75°处，分别位于内、外腹板的对称纵截面上的L、S节点为研究对象，如图1(b)所示。

2  H96矩形管绕弯回弹有限元模型的建立

2.1  矩形管的几何尺寸与材料参数

矩形管的截面尺寸为24.86 mm(w)×12.2 mm (h)×1 mm(t)，材料为H96黄铜，采用各向同性材料硬化模型，其屈服条件f如公式(5)所示，

                 (5)

式中：s为偏应力张量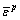；为等效塑性应变；ε₀、K和n是H96矩形管材料常数，通过单向拉伸试验获得，分别为ε₀=0.010 4，n=0.51，K=588.17 MPa。其他材料参数，如弹性模量和泊松比分别为92.82 GPa和0.324。

2.2  压块及其边界条件

为了同时实现压块夹紧管子并向前助推这两种动作，建模时将夹块分为两部分：一部分用来施加夹紧压力，称为传力块；另一部分提供助推速度，称为传动块，如图2所示。传力块与管子存在摩擦约束，并沿加载方向具有运动自由度；传动块仅与传力块接触，并依靠刚体之间的摩擦作用推动传力块向前运动，进而推动管子向前运动。为了避免将管子夹扁，给出了夹持压力的临界值σ_cl求解公式，如式(6)所示，

                                 (6)

式中：σ_p近似等于管子的压缩失稳应力，H96矩形管的压缩试验获得σ_p的值介于180~200 MPa之间；S为压块与管子的接触面积；S_p为压块被施加压力的面积。

图2  包含传力块和传动块两部分的压块的几何模型

Fig. 2  Geometry model of pressure die including two parts of load transfer die and driven die

2.3  绕弯回弹全程有限元模型的建立

为了模拟回弹和截面畸变，采用S4R壳单元分别建立考虑压块载荷边界条件的弯曲过程有限元模型和回弹过程有限元模型，如图3所示。其中，弯曲过程的有限元模型涉及多模具约束力的加载条件和材料的大变形和大位移，采用动态显式算法计算(见图3(a))。

图3  矩形管绕弯回弹全程有限元模型

Fig. 3  Finite element model of whole bending-springback process of rectangular tube

而回弹过程的有限元模型采用静态隐式算法，是通过导入绕弯成形结束后的单元、节点、几何位移和初始应力应变场而建立的(见图3(b))。

2.4  有限元模型可靠性验证

试验和模拟的基本条件，如模具的运动速度、间隙、弯曲半径等，都是一致的，如表1所列。

表1  试验和模拟的基本条件

Table 1  Experimental and simulation conditions

试验中，压块、防皱块、弯曲模与矩形管之间的摩擦为干摩擦，夹块与管坯的接触面上刻有防滑皱纹，芯棒-芯头与管坯之间采用航空油润滑。模拟时采用库伦摩擦条件，根据文献[15-16]，模具与管坯间的库伦摩擦因数如表2所列。

表2  模具与H96矩形管之间的摩擦条件

Table 2  Frication conditions between dies and rectangular H96 tube

采用所建有限元模型和表1、表2中的条件，模拟得到的90°H96矩形弯管与试验结果的对比如图4(a)所示，可以看到二者非常吻合。同时，图4(b)对比了图4(a)中弯管在试验和模拟条件下对称纵截面的高度变形量，可以看到模拟结果和试验结果非常接近，最大误差为23.86%。为了进一步验证模型的可靠性，图4(c)还给出了芯棒-芯头与管坯间隙为0.5 mm情况下的90°弯管模拟与试验结果的对比，由图4(c)可知，试验和模拟所得的矩形管内腹板都出现了起皱现象，二者起皱波的个数相同。且图4(d)相应地给出了该弯管对称纵截面的高度变形量的数值模拟与试验实测值，二者的最大误差约为24%。由上述分析可知，采用所建H96矩形管绕弯回弹全程有限元模型可以可靠地预测截面变形。

此外，采用所建有限元模型和表1、表2中模拟条件预测的不同弯曲角度下的回弹角如图4(e)所示，通过与试验数据对比发现，回弹角随弯曲角的变化趋势与试验结果一致，且二者的平均误差仅为10.33%。因此，所建绕弯回弹全程有限元模型可以准确地预测H96矩形管绕弯回弹。

3  压块的边界条件对H96矩形管绕弯回弹和截面变形的影响

压块的边界条件包括压块与管坯间的摩擦因数、夹持压力和助推速度。表3所列为所研究边界条件参数的取值范围。

表3  模拟用压块边界条件参数范围

Table 3  Parameters of pressure die boundary conditions in simulation

图4  H96矩形管绕弯成形试验和模拟结果对比

Fig. 4  Comparison of experimental and simulation results of rotary-draw bending

3.1  摩擦因数对回弹和截面变形的影响

通过模拟发现，当压块与管坯间摩擦因数分别为0、0.19和0.3时，矩形管绕弯回弹角分别为1.96°、1.71°和1.50°。这是由于摩擦因数越大，压块的助推能力越强，回弹量也就越小。为了进一步解释这一现象，图5(a)和(b)分别给出了弯曲角为90°时L、S节点(见图1(b))随弯曲进程的切向应力变化。可以看到，抽芯阶段是弹性变形过程，应力的大小基本不发生变化，矩形管的回弹量的大小主要受弯曲进程影响。而在弯曲进程中，摩擦因数越大，切向应力的波动幅度越大，但最终的切向应力越小，所以回弹量也越小。这同时也说明了芯棒填充区域的应力波动和随后弯曲阶段内的切向应力变化对回弹量都有着重要影响。

图6(a)和(b)分别显示沿弯曲方向75°截面上L、S节点间高度变形量和椭圆程度在90°弯曲进程中的变化。由图6(a)和(b)可以看到，节点在经过芯棒填充区域时，无论摩擦因数如何变化，截面变形量都几乎不变。而离开芯头填充区域时，摩擦因数为0.19和0.3时的高度变形量比摩擦因数为0时的小很多，同时L节点上的椭圆程度也较摩擦因数为0时的小，但S节点上的椭圆程度较摩擦因数为0时的大，这说明压块的摩擦因数对高度变形和外腹板椭圆程度的影响可能相反。综合回弹角考虑，压块的摩擦因数选取0.3较好。

3.2  夹持压力对回弹和截面变形的影响

利用公式(6)和试验得到的管子的压缩失稳应力，可算出压块的临界夹持压力在30 MPa左右。图7所示为矩形管回弹角随夹持压力的变化趋势。由图7可知，夹持压力越大，回弹角越小。当夹持压力为27 MPa时，其对应的回弹角要比夹持压力为3 MPa时的小0.76°。

图8(a)所示为不同夹持压力下矩形管截面高度变形量Δh_i沿弯曲方向的分布，从图8(a)中可以看出，夹持压力越大，Δh_i相对越小。图8(b)给出了L、S节点间Δh_i在90°弯曲进程中的变化。由图8(b)中可以看出，在芯头填充区域，不同夹持压力下的Δh_i变化非常小。但是在离开芯头填充区以后，高度变形量开始剧烈增大，而夹持压力越小，这种剧增的幅度就越大。抽芯过程的高度变形量Δh_i几乎不发生变化，所以，最终夹持压力越大，Δh_i越小。

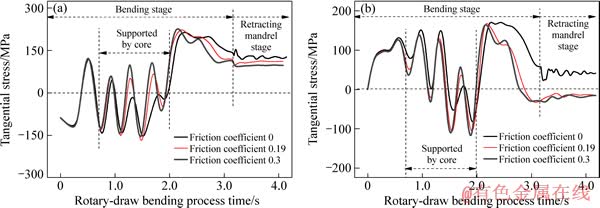
图5  不同摩擦因数下L、S节点在90°弯曲进程中的切向应力变化

Fig. 5  Tangential stress variation of nodes L (a) and S (b) under different friction coefficients during 90° bending process

图6  不同摩擦因数下90°弯曲进程中的截面变形量

Fig. 6  Section deformation under different friction coefficients during 90° bending process

图7  矩形管回弹角随压块夹持压力的变化

Fig. 7  Variation of springback angle of rectangular tube with clamping pressure of pressure die

图9(a)所示为不同夹持压力下矩形管外腹板椭圆化程度Δl_i沿弯曲方向的分布。由图9(a)可知，夹持压力越大，Δl_i越大。而内腹板椭圆程度ΔL_i随夹持压力的变化趋势同Δl_i一致，但由于差距不如Δl_i明显，不再分析。上述现象意味着压块助推作用的增大使矩形管纵截面的椭圆率增大。图9(b)给出了S节点上椭圆程度在90°弯曲进程中的变化。由图9(b)可以看到，在有芯头填充的区域，不同夹持压力下的椭圆程度同样差别不大。但是在离开芯头填充区以后，夹持压力越大，椭圆程度越大，最终形成如图9(a)所示的Δl_i沿弯曲方向的分布规律。

图8  不同夹持压力下的矩形管截面高度变形量Δh_i

Fig. 8  Sectional height deformation Δh_i of rectangular tube under different clamping pressures

图9  不同夹持压力下的矩形管纵截面椭圆化程度Δl_i

Fig. 9  Longitudinal sectional ovalization Δl_i of rectangular tube under different clamping pressures

由上述研究可知，夹持压力对矩形管截面高度变形量和椭圆程度的影响是截然相反的，需要综合考虑如何选取夹持压力的值。在此分别引入相对高度变形量δh_i、内腹板相对椭圆程度δL_i和外腹板相对椭圆程度δl_i的计算公式，

                                  (7)

                                 (8)

                                  (9)

由图8(a)和图9(a)中数据知，3、9、18、27 MPa夹持压力下，Δh_i沿弯曲方向的平均值分别为7.95%、6.06%、5.07%、4.45%，这4个数据间的最大差值为3.50%。在3、9、18、27 MPa夹持压力下，ΔL_i沿弯曲方向的平均值分别为3.63%、3.82%、4.33%、4.83%，数据间的最大差值为1.20%；而Δl_i沿弯曲方向的平均值分别为0.71%、1.32%、1.93%、2.43%，数据间最大差值为1.72%。比较上述数值可知，Δh_i受夹持压力的影响程度要大于ΔL_i和Δl_i的，且相对变形程度较ΔL_i和Δl_i的严重。综合考虑夹持力对回弹的影响，所以，采用夹持压力27 MPa为佳。

3.3  助推速度对回弹和截面变形的影响

表3所列为标准助推速度22.96 mm/s是根据助推速度与矩形管外腹板绕弯线速度一致计算得到的，而其他助推速度值则是按照0、0.5、1.25、1.5倍标准助推速度选取的。图10所示为不同助推速度下矩形管回弹角的结果。由图10可看出，助推速度对回弹量的影响不像夹持压力那样明显。在助推速度小于22.96 mm/s时，随着速度的增加，90°和45°弯管的回弹角略有下降；在助推速度大于22.96 mm/s时，随着速度的增加，90°和45°弯管的回弹角先增加后下降，34.44 mm/s助推速度所对应的回弹角最小。

然而，模拟发现，当助推速度小于标准助推速度时，成形角度大于60°的弯管会在芯头填充不到区域发生较大的截面塌陷。图11所示为11.48 mm/s 助推速度下的90°弯管半截面示意图。由图11可以看到，在非芯头填充区域，内、外腹板的截面出现较严重的塌陷。因此，不能在整个弯曲进程中一直采用低于标准值的助推速度。图12所示为助推速度下Δh_i沿弯曲方向的分布。由图12可以看出，这3条曲线起初非常接近，但在接近夹块端的弯曲截面内，过高的助推速度使得Δh_i要大于其他助推速度下的值。

综上所述，助推速度高于或低于标准助推速度值，都会对回弹量产生一定的影响，也会增大非芯头填充区域内的截面畸变量。

图10  不同助推速度下的矩形管回弹角

Fig. 10  Springback angles of rectangular tube under different boosting velocities

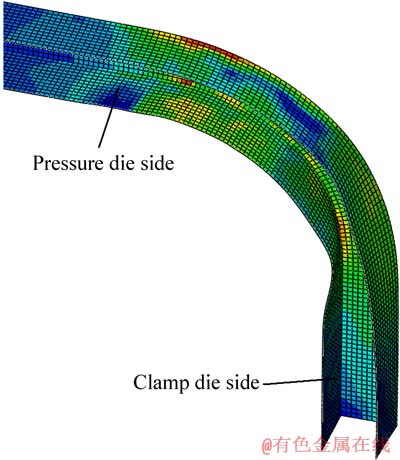
图11  助推速度11.48 mm/s下的90°弯管半截面

Fig. 11  Half profile of 90° bent tube under boosting velocity of 11.48 mm/s

图12  不同助推速度下Δh_i沿弯曲方向的分布

Fig. 12  Distribution of Δh_i obtained under different boosting velocities along bending direction

4  基于变助推速度的压块边界条件组合对矩形管绕弯截面变形和回弹的影响

由以上的研究结果得知，摩擦因数0.3和夹持压力27 MPa可有效控制回弹和截面变形，应该将其作为参数组合的基础。而结合图5、6、8(b)、9(b)、11和12的结果可知，在芯棒填充区域可利用较快或较慢的助推速度影响切向应力的大小进而降低回弹量，且不会加剧截面变形。所以采用表4中4组工艺参数组合，研究如何综合利用压块的工艺参数控制矩形管绕弯的截面变形和回弹。其中，参数组合1为1.4节中验证有限元模型时所用试验和模拟条件。参数组合3和4采用变助推速度，即在有芯头支撑的60°弯曲区域，压块速度略低于标准值(组合3)，或者为1.5倍的标准运动速度(组合4)，而离开芯头填充区后，压块的速度恢复为标准速度。

表4  4组压块边界条件参数组合

Table 4  Four groups of parameters combinations of pressure die boundary conditions

图13所示为4组工艺参数对应的回弹角。由图13可以看到，组合1条件下得到的回弹角要远大于组合2~4条件下得到的回弹角。当弯曲角度小于90°时，参数组合4得到的回弹角平均值最小，比组合1的平均值小55.31%，且在成形角度为30°时，组合4下的回弹角甚至只有0.37°；当弯曲角度为90°时，组合2~4下的回弹角比较接近，组合3下的最小值为1.12°，比组合1得到的回弹角小0.86°；当弯曲角度大于90°时，组合3得到的回弹角比其他组合的都小，比组合1的平均值小36.45%。由此可见，当弯曲角度小于90°时，组合4是控制回弹的压块最佳参数组合，而当弯曲角度大于等于90°时，组合3是控制回弹的最佳选择。

图13  4组参数组合下的回弹角

Fig. 13  Springback angles obtained under four groups of parameter combinations

图14所示为4种参数组合下60°、90°、120°弯管Δh_i沿弯曲方向的分布情况。由图14可见，在这3种弯曲角度下，组合1对应的Δh_i平均值和最大值都较其他组的大。对于60°弯管，组合4下的Δh_i平均值和最大值都是全组中最小的，如果采用组合4的成形条件，则平均能够降低高度畸变1.79%。对于90°弯管，组合2和4下的Δh_i平均值和最大值都是全组中最小的，其次是组合3的。如果采用组合2或4的成形条件，则最大能够降低高度畸变7.05%；如果采用组合3，则此值为5.98%。对于120°弯管，与上述情况略有不同的是，组合3获得的Δh_i最大值是全组中最小的，如果采用组合3的成形条件，则高度畸变量最大降低了6.35%。

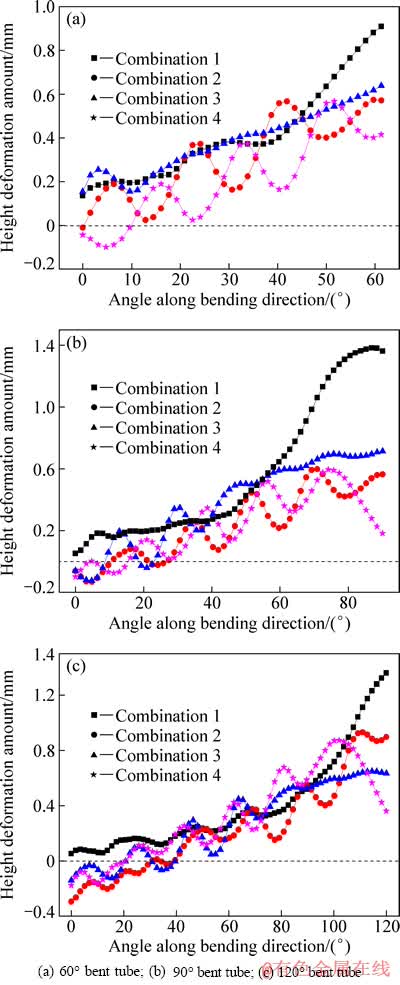
图14  4组参数组合下沿弯曲方向分布的Δh_i

Fig. 14  Distributions of Δh_i along bending direction under four groups of parameter combinations

图15所示为4组参数组合下60°、90°和120°弯管的变形量(ΔL_i)分布。由图15可以看到，当管子的弯曲角度为60°时，组合1、3、4对应的椭圆程度基本一致，组合2的变形量(ΔL_i)在小于25°的弯曲段内较其他组的偏小，而在其余弯曲段偏大。当弯曲角度为90°和120°时，在大于25°的弯曲段内，组合1的ΔL_i始终是全组中最小的，组合4的ΔL_i始终是最大的，因此，组合4不能被用于弯曲角度大于等于90°的绕弯成形。以组合1为基准，当弯管弯曲90°和120°时，采用组合2，ΔL_i的平均值分别升高了2.37%和1.31%；而采用组合3，ΔL_i的平均值分别升高了1.37%和1.68%。外腹板椭圆程度Δl_i在4种参数组合下的分布趋势，同图15完全一致。当弯管弯曲90°和120°时，采用组合2，Δl_i的平均值分别升高了2.47%和1.24%；采用组合3，Δl_i的平均值分别升高了1.46%和1.55%。综合比较，建议采用组合3弯曲大于等于90°的弯管。

图15  4组参数组合下沿弯曲方向分布的ΔL_i

Fig. 15  Distributions of ΔL_i along bending direction under four groups of parameter combinations

综上所述，采用压块参数组合4弯曲小于90°的弯管，可降低回弹量55.31%，平均降低60°弯管高度畸变量1.79%。采用压块参数组合3成形大于等于90°的弯管，可降低回弹量36.45%，分别能够最大降低90°、120°弯管高度畸变量5.98%和6.35%。但是无论是组合3还是组合4，内、外腹板的椭圆程度都会相应地升高。

5  结论

1) 摩擦因数越大，夹持压力越大，压块的助推能力越强，回弹量越小，横截面高度变形越小。但压块助推作用的增大会增大矩形管纵截面的椭圆率，压块对横、纵截面畸变的作用完全相反。横截面高度变形量受夹持压力的影响程度要大于纵截面的。综合上述结果，摩擦因数0.3和夹持压力27 MPa为控制回弹和截面变形的最佳工艺选择。

2) 在绕弯过程中，助推速度一直低于标准值时，角度大于60°的弯管会在芯头填充不到的区域内发生较大的截面塌陷，助推速度一直高于标准值时，接近夹块端的矩形管横截面高度变形量会大于标准助推速度下的值。在有芯头填充的区域，不同压块参数下的横截面高度变形和内、外腹板椭圆程度变化非常小。

3) 采用变助推速度的压块边界条件组合方案，达到同时降低回弹量和横截面高度变形量的目的。通过模拟研究发现，采用压块参数组合4弯曲小于90°的弯管，可降低回弹量55.31%，平均能够降低60°弯管高度变形量1.79%。采用压块参数组合3成形大于等于90°的弯管，可降低回弹量36.45%，分别最大能够降低90°、120°弯管高度变形量5.98%和6.35%。

REFERENCES

[1] 刘 伟, 刘红生, 邢忠文, 曹克利. 高强钢板冲压成形的回弹规律与工艺参数研究[J]. 材料科学与工艺, 2010, 18(6): 758-761.

LIU Wei, LIU Hong-sheng, XING Zhong-wen, CAO Ke-li. Study on process parameters and springback rule for stamping of high strength steel sheet[J]. Materials Science and Technology, 2010, 18(6): 758-761.

[2] 张尧武, 曾卫东, 戴 毅, 赵永庆, 周义刚, 王凯旋. 基于虚拟正交试验的热推弯管工艺参数优化设计[J]. 塑性工程学报, 2009, 16(6): 91-95.

ZHANG Yao-wu, ZENG Wei-dong, DAI Yi, ZHAO Yong-qing, ZHOU Yi-gang, WANG Kai-xuan. Optimal design of technological parameters for hot-pushing pipe-bending based on virtual orthogonal experiment[J]. Journal of Plasticity Engineering, 2009, 16(6): 91-95.

[3] LI H, YANG H, ZHAN M, KOU Y L. Deformation behaviors of thin-walled tube in rotary draw bending under push assistant loading conditions[J]. Journal of Materials Processing Technology, 2010, 210: 143-158.

[4] LI C, YANG H, ZHAN M, XU X D, LI G J. Effects of process parameters on numerical control bending process for large diameter thin-walled aluminum alloy tubes[J]. Transactions of Nonferrous Metals Society of China, 2009, 19(3): 668-673.

[5] ZHAO G Y, LIU Y L, YANG H, LU C H. Cross-sectional distortion behaviors of thin-walled rectangular tube in rotary-draw bending process[J]. Transaction of Nonferrous Metals Society of China, 2010, 20(3): 484-489.

[6] 李雁鹏, 吴建军. 非平面弯管成形过程的回弹补偿研究[J]. 锻压技术, 2009, 34(1): 89-92.

LI Yan-peng, WU Jian-jun. Study on spring-back compensation for non-plane tube bending process[J]. Forging & Stamping Technology, 2009, 34(1): 89-92.

[7] 张 深, 吴建军. 管材空间绕弯回弹补偿方法研究[J]. 西北工业大学学报, 2011, 29(5): 811-817.

ZHANG Shen, WU Jian-jun. A new method for springback compensation for the bending of a thick-walled non-planar tube[J]. Journal of Northwestern Polytechnical University, 2011, 29(5): 811-817.

[8] LIU W, YANG Y Y, XING Z W, ZHAO L H. Springback control of sheet metal forming based on the response-surface method and multi-objective genetic algorithm[J]. Materials Science and Engineering A, 2009, 499: 325-328.

[9] KATAYAMA T, NAKAMACHI E, NAKAMURA Y, OHATA T, MORISHITA Y, MURASE H. Development of process design system for press forming—Multi-objective optimization of intermediate die shape in transfer forming[J]. Journal of Materials Processing Technology, 2004 155/156: 1564-1570.

[10] CLAUSEN A H, HOPPERSTAD O S, LANGSETH M. Sensitivity of model parameters in stretch bending of aluminium extrusions[J]. International Journal of Mechanical Sciences, 2001, 43: 427-453.

[11] MILLER J E, KYRIAKIDES S, BASTARD A H. On bend-stretch forming of aluminum extruded tubes I: Experiments[J]. International Journal of Mechanical Sciences, 2001, 43: 1283-1317.

[12] CORONA E. A simple analysis for bend-stretch forming of aluminum extrusions[J]. International Journal of Mechanical Sciences, 2004, 46: 433-448.

[13] ZHU H, STELSON K A. Modeling and closed-loop control of stretch bending of aluminum rectangular tubes[J]. Journal of Manufacturing Science and Engineering, 2003, 125: 113-119.

[14] ZHU Y X, LIU Y L, YANG H. Sensitivity of springback and section deformation to process parameters in rotary draw bending of thin-walled rectangular H96 brass tube[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(9): 2233-2240.

[15] 赵刚要. 薄壁矩形管数控绕弯成形起皱及成形极限研究[D]．西安: 西北工业大学, 2010.

ZHAO Gang-yao. Study on wrinkling behaviors and limit during NC rotary-draw bending process of thin-walled rectangular tube[D]. Xi’an: Northwestern Polytechnical University, 2010.

[16] 徐 灏. 机械设计手册[M]. 第一卷. 北京: 机械工业出版社, 1991.

XU Hao. Machinery’s handbook[M]. 1st ed. Beijing: China Machine Press, 1991.

(编辑  李艳红)

基金项目：国家自然科学基金资助项目(50975235)；“111”引智计划资助项目(B08040)

收稿日期：2013-03-14；修订日期：2013-10-24

通信作者：刘郁丽，教授，博士；电话：029-88460212-803；E-mail: lyl@nwpu.edu.cn