J. Cent. South Univ. (2012) 19: 1081-1085
DOI: 10.1007/s11771-012-1112-4
Optimum blending of iron ore from Choghart stockpiles
by using goal programming
J. Gholamnejad, S. Kasmaee
Department of Mining and Metallurgical Engineering, Yazd University, Yazd 89195-741, Iran
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Iron and steel industry is an important sector of Iran’s economy. Choghart iron ore mine is an important iron ore producer of Iran steel industry. Phosphorous contained in the iron ore concentrates of Choghart mine has a detrimental effect on the steel making process, whereby this causes cracks to form in the refractory lining of blast furnaces. In the past, about 1.43 Mt of low-grade and 4.53 Mt of high-phosphorous materials had been transported to low grade and high phosphorous stockpiles, respectively, for future beneficiation. As a result of the progressive depletion of high-grade ore and establishment of beneficiation plant in Choghart, exploitation of these two stockpiles in this mine became an important issue. In this work, a linear goal programming (GP) model was developed in order to determine the optimum iron ore blend in terms of quality from low grade and high phosphorous stockpiles of Choghart mine. The model was solved by the SOLVER V.9 program. Results show that feeding with acceptable quality (w(Fe)≥50% and w(P)≤1.2%, mass fraction) materials can be blended from stockpiles that satisfy the needs of the Choghart processing line.
Key words: processing plant; short term production scheduling; goal programming; stockpile
1 Introduction
The Choghart apatite-bearing iron oxide deposit (55°28′2″E, 31°42′00″N) is locatedin the Bafq mining district of Central Iran, 12 km northeast of Bafq town and 125 km southeast of Yazd city (see Fig. 1). There are more than 80 identified magnetic anomalies in the Bafq mining district, and the region is believed to host over 2 Gt of iron oxide ore [1]. Most of the deposits are unexploited or only partially mined. Choghart is the first deposit of its kind exploited in the Bafq mining district. The remaining total reserve of Choghart is estimated to be 200 Mt. The first apatite-rich iron oxide ore was shipped to Isfahan steel mill (the largest mill in Iran) in 1971, and since then, Choghart has remained the main supplier of iron ore to this mill [2]. At this mine, from 1993 to 2003, about 1.43 Mt of lumpy low-grade (w(Fe)<50%, mass fraction) and 4.53 Mt of high- phosphorous (w(Fe)>50% and w(P)>0.6%, mass fraction) materials had been transported to low grade (LG) and high phosphorous (HP) stockpiles, respectively. Materials with w(Fe)≥50% and w(P)≤0.6% (mass fraction) were designated for the crush feed. These stockpiles were formed for storage of excessive production and storage of low grade ore for possible future processing. The quality of ore in these stockpiles is extremely variable through the horizontal and vertical directions in terms of Fe and P. Although the P and Fe contents are quiet different between the two stockpiles, they are fluctuant in their distribution. The increased rate of exploitation of iron ore has resulted in rapid depletion of known high grade iron ore deposit. Establishment of Choghart beneficiation plant in order to produce 3.2 Mt/a of iron concentrate, leads to realization of the economic potential of these piles as ore reserves. This 3.2 Mt/a fine concentration beneficiation plant consists of two independent process lines:
1) Choghart process line, with the feed capacity of 2.3 Mt/a and feed quality of w(Fe)>50% and w(P)<1.2% to produce 1.6 Mt/a of fine concentrate.
2) Sechahoun process line, with the feed capacity of 3.4 Mt/a and feed quality of w(Fe)>32% to produce 1.6 Mt/a of fine concentrate.
Milling costs depend on the quality of the feeding materials for the beneficiation process. Therefore, constantly feeding the processing plant with the optimum quality materials has a considerable influence on the overall economy of the whole operation. As a result, it is needed to develop an effective short term scheduling procedure suitable for stockpiles, considering their geometry and geology.
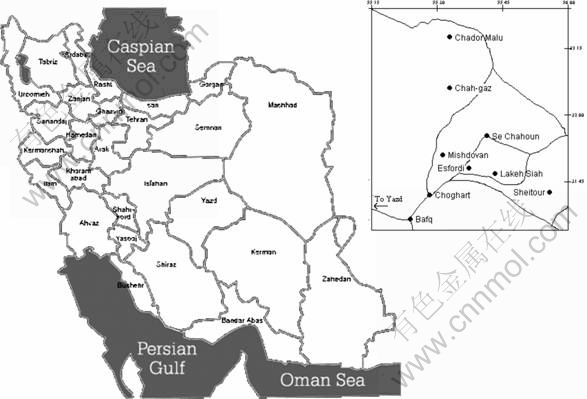
Fig. 1 Geographic map for location of Choghart deposit in Bafq mining district, Iran
2 Input data preparation for short term production scheduling
In order to prepare data for short term planning, at first, both stockpiles have been computerized and grouped into mining units or reserve records [3]. Also these stockpiles are divided into three benches according to the progress of stockpile formation; benches of 1 158, 1 163 and 1 165 m for HP pile and benches of 1 150, 1 155 and 1 160 m for LG one. Each block has been assigned the values of interest using geostatistical analysis by the aid of SURPAC V.6.0 software [4]. The qualitative and quantitative characteristics of these two stockpile block models are given in Table 1.
Table 1 Characteristics of Choghart stockpiles block model [3]

The next step is the determination of Choghart processing line constraints. The short term production scheduling in this work refers to a time frame of monthly planning. The average grade of the ore tonnage mined in each monthly period is constrained to be between 50% and 52% (mass fraction) of Fe and between 0.8% and 1.2% (mass fraction) of P, and the minimum and maximum periodical ore production from these two stockpiles are limited to be between 6×104 and 9×104 t per month. The stockpiles were scheduled to be removed for five months of production using the Integer programming model. All the blocks in the stockpiles model are considered for scheduling.
3 GP model for production scheduling of Choghart stockpiles
Single objective linear programming has been used to solve production scheduling problems. This model consists of only one objective function that is subjected to a set of constraints. Some goals like quality and quantity of produced ore, location of working benches, productivity of mining equipments and processing conditions can be taken into consideration in the constraints setting up. These goals are sometimes incompatible and no feasible solution can be found in single objective optimization. Here, goal programming (GP) is suitable, because in GP, owing to the deviation variables included, the best solution can be obtained [5]. The term “goal programming” was first coined by CHARNES and COOPER [6], who originally developed the mathematical model to address the problem of infeasibilities caused by incompatible constraints.
The presented GP formulation will determine the removal plan of stockpiles blocks as its optimal solution value in the form of linear programming (LP) with integer variables. This model consists of variables, parameters, objective function and constraints. The variables and parameters used in the LP model are defined below.
3.1 Objective function
The objective function of this model is constructed as minimization of a penalty function. This function is defined as the total cost of deviations from the planned average ore grade targets. It is expressed as
+
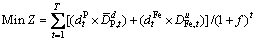 (1)
(1)
In order to write the objective function, a constant value is assigned for each cost parameter representing the cost at time 0 (base cost). Then, the f factor is introduced to quantify the penalty cost at different time periods by discounting the base cost [7].
3.2 Model constraints
Grade blending constraints are important constraints that control the quality of ore to be sent to the mill in each period. In iron ore mine, Fe, ratio of Fe/FeO, P, Si and S are important factors in mill feed control. In this model, Fe and P are considered as critical parameters, and the grade blending constraints can be written as
 (2)
(2)

 (3)
(3)
 (4)
(4)
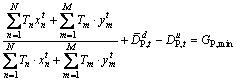 (5)
(5)
The constraints Eqs. (2)-(5) are written for each of the T times periods (t=1, 2, …, T).
In Choghart processing plant, the constraints related to the minimum Fe average grade and P maximum average grade of ore sent to the mill are tight constraints that should not violated. But those related to the maximum Fe average grade and P minimum average grade of ore sent to the mill are to some extent flexible constraints, therefore the deviation from grade blending targets is only permitted about Eqs. (3) and (5).
Other constraints like slope constraints, reserve constraints, mine and mill capacity constraints, space for operation equipments are also included in this model that are not discussed in this work [8-10].
4 Implementation of LP model on Choghart stockpiles
The presented mathematical model was applied to six benches of HP and LG stockpiles and then solved with the SOLVER V.9 program. The resulted production schedule on benches 1 150 m of HP stockpile and 1 155 m of LG stockpiles are shown in Figs. 3 and 4. The numbers in these figures represent the block extraction sequences, all the block with the same number are removed from these two piles simultaneously, and then blended and sent to the mill.
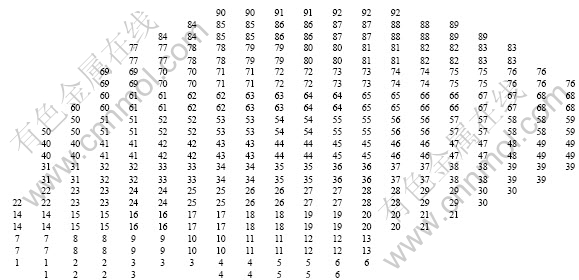
Fig. 3 Scheduling map of ore and waste block at level 1 150 m of HP stockpile (“1”, “2” and so on represent sequential monthly plan)

Fig. 4 Scheduling map of ore and waste block at level 1 155 m of LG stockpile (“1”, “2” and so on represent sequential monthly plan)
This modeling shows that with a good blending strategy, a continuous feeding can be provided for the mill with internal blending from these piles without any need to the ore from the open pit or other stockpiles. But it should be noted that a blending site is needed for dumping and homogenizing of ore from two stockpiles.
5 Conclusions
1) A goal programming model has been developed for stockpile short term scheduling. After establishing geological data files, the model is set up. The objective function of this model is constructed as minimization of the total cost of deviations from the planned average ore grade targets. This function is subjected to the ore quality and quantity and other geometrical and operational constraints.
2) The presented linear programming model is applied to Choghart HP and LG stockpiles in order to provide feed for Choghart processing plant. This model is then solved via SOLVER V.9 package and determined how many iron ore blocks on each bench of stockpiles should be mined out simultaneously to satisfy the Choghart processing line. It is concluded that, in spite of grade complexities existing in LG and HP stockpiles, goal programming is a powerful tool for solving multi-objective decision making problems, because of its practicality and flexibility. The proposed model generates feasible scheduling patterns in terms of quality, quantity and operational constraints.
Nomenclature
T
The total number of production periods, or stockpile life
N
The number of blocks considered for scheduling in HP stockpile
M
The number of blocks considered for scheduling in LG stockpile

A binary variable, it is assigned, 1, if block n from HP stockpile is mined in period t, and assigned 0 otherwise
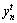
A binary variable, it is assigned, 1, if block m from LG stockpile is mined in period t, and assigned 0 otherwise
c(Fe)n
Fe content of block n in HP stockpile block model
c(Fe)m
Fe content of block m in LG stockpile block model
c(P)n
P content of block n in HP stockpile block model
c(P)m
P content of block m in LG stockpile block model
GFe, max and GFe, min
The targeted minimum and maximum Fe average grade of the ore material to be processed in a period
GP, max and GP, min
The targeted minimum and maximum P average grade of the ore material to be processed in a period
Tn and Tm
The ore tonnage inside block n and m in HP and LG stockpiles, respectively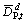 and
and 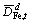
The downward deviation from GFe, max and GP, min in period t
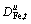 and
and 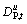
The upward deviation from GFe, max and GP, min in period t
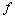
+
Risk discount rate
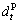 and
and 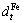
Unit cost of 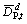 and
and 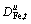 respectively for the objective function. These are the factor of priority
respectively for the objective function. These are the factor of priority
References
[1] DALIRAN F. REE geochemistry of Bafq Apatites, Iran: Implication for the genesis of Kiruna-type iron ores [C]// STANCLY et al, Eds. Proceedings of Mineral Deposits and Processes to Processing. Balkema, Netherlands, 1999: 631-634.
[2] MOORE F, MODABBERI S. Origin of choghart iron oxide deposit, bafq mining district, entral Iran: New isotopic and geochemical evidence [J]. Journal of Sciences, Islamic Republic of Iran, 2003, 14(3): 259-269. (in Iranian)
[3] KASMAEE S, GHOLAMNEJAD J, YARAHMADI A, MOJTAHEDZADEH S A. The reserve estimation of high phosphorous stockpile in Choghart Iron mine of iran by using geostatistical modeling [J]. Journal of Mining Science and Technology, 2010, 20: 0855-0860.
[4] Surpac Usres Manual, Version V5.2-D, Surpac Minex Group, 2006.
[5] ZHANG You-di, CAI Qing-xiang, WU Li-xin, ZHANG Da-xian. Combined approach for surface mine short term planning optimization [C]// Proceedings of 23rd International Symposium 1992-Application of Computers and Operations Research, Chapter 49 - Mine Design and Planning – II, 1992: 499-507.
[6] CHARNES A, COOPER W W. Management models and industrial applications of linear programming [M]. New York: John Wiley & Sons, 1961: 469-859.
[7] RAMAZAN S, DIMITRAKOPOULOS R. Stochastic optimization of long-term production scheduling for open pit mines with a new integer programming formulation [C]// Prpceedomgs of Ore body Modeling and Strategic Mine Planning-Uncertainty and Risk Management International Symposium. Perth, Australia, 2004: 353-359.
[8] GHOLAMNEJAD J, OSANLOO M, KARIMI B. A chance- constrained programming approach for open pit long-term production scheduling in stochastic environments [J]. The Journal of the South African Institute of Mining and Metallurgy, 2006, 106: 105-114.
[9] GHOLAMNEJAD J, OSANLOO M, KHORRAM E. A chance constrained integer programming model for open pit long- termproduction planning [J]. IJE Transactions A: Basics, 2008, 21(4): 307-318.
[10] GHOLAMNEJAD J. A zero-one integer programming model for open pit mining equences [J]. The Journal of the South African Institute of Mining and Metallurgy, 2008, 108: 759-762.
(Edited by DENG Lü-xiang)
Received date: 2011-06-30; Accepted date: 2011-10-17
Corresponding author: J. Gholamnejad, Assiociate Professor; Tel: +98-351-8122587; E-mail: j.gholamnejad@yazduni.ac.ir