
ARTICLE
J. Cent. South Univ. (2019) 26: 2272-2280
DOI: https://doi.org/10.1007/s11771-019-4172-x

Soft measurement model on torque of alternating current electrical dynamometer including copper loss and iron loss
ZHONG Ding-qing(钟定清)1, 2, WANG Ai-lun(王艾伦)1, HE Qian(何谦)1
1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. School of Mechanical Engineering, Hunan Institute of Engineering, Xiangtan 411104, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Alternating current electrical dynamometer is a common device to measure the torque of engines, such as the gasoline engine. In order to solve the problems such as high cost, high energy consumption and complicated measurement system which exists in the direct measurement on the torque of alternating current electrical dynamometer, copper loss and iron loss are taken as two key factors and a soft-sensing model on the torque of alternating current electrical dynamometer is established using the fuzzy least square support vector machine (FLS-SVM). Then, the FLS-SVM parameters such as penalty factor and kernel parameter are optimized by adaptive genetic algorithm, torque soft-sensing is investigated in the alternating current electrical dynamometer, as well as the energy feedback efficiency and energy consumption during the measurement phase of a gasoline engine loading continual test is obtained. The results show that the minimum soft-sensing error of torque is about 0.0018, and it fluctuates within a range from -0.3 to 0.3 N·m. FLS-SVM soft-sensing method can increase by 1.6% power generation feedback compared with direct measurement, and it can save 500 kJ fuel consumption in the gasoline engine loading continual test. Therefore, the estimation accuracy of the soft measurement model on the torque of alternating current electrical dynamometer including copper loss and iron loss is high and this indirect measurement method can be feasible to reduce production cost of the alternating current electrical dynamometer and energy consumption during the torque measurement phase of a gasoline engine, replacing the direct method of torque measurement.
Key words: torque; fuzzy theory; least square support vector machine; alternating current electrical dynamometer
Cite this article as: ZHONG Ding-qing, WANG Ai-lun, HE Qian. Soft measurement model on torque of alternating current electrical dynamometer including copper loss and iron loss [J]. Journal of Central South University, 2019, 26(8): 2272-2280. DOI: https://doi.org/10.1007/s11771-019-4172-x.
1 Introduction
Alternating current electrical dynamometer is an important testing equipment with full function (including electric conditions and power generation working conditions) and high performance [1, 2], using motor to measure the output torque of a variety of power machinery shafts and combining rotational speed to determine the power of measured devices [3]. Alternating current electrical dynamometer is widely used in dynamometer experiments of power machine with medium and small power or mini-low power, such as testing the power of engine [4], for it has the advantages of high reliability [5], strong maintainability [6], bidirectional loading and traction behavior, energy feedback, etc., compared with direct current (DC) electrical dynamometer. In addition, it also can be used as the loading equipment of engines [7, 8], gearbox, reducer and transmission for testing their power transmission [9].
According to the principle of alternating current electrical dynamometer, rotational speed and mechanical torque are the key measurement parameters in application while the common measurement method in the market is direct measurement, such as transforming the structure of alternating current asynchronous motor and installing high-precision torque meter or torque flange for detection, which generally has special requirements for the motor and increases the complexity of measurement system due to the addition of transmission system [10, 11], leading to the quite expensive cost of alternating current electrical dynamometer [12].
Due to the crisis of energy shortage [13, 14], a new idea of indirect measurement for the torque of alternating current electrical dynamometer was gotten based on the rapid development and its successful application of soft measurement technology [15, 16]. Soft measurement technology [17, 18] is a feasible solution for measuring torque of alternating current (AC) electrical dynamometer with low cost and high sensitivity.
In recent years, for the problems of alternating current electrical dynamometer in the experiment process such as nonlinearity, high cost and high energy consumption [19], in this paper, as an indirect detection method, soft sensor on the torque of alternating current electrical dynamometer based on fuzzy least square support vector machines (FLS-SVM) [20, 21] is proposed according to the unique advantages such as requiring of less sample data [22], relearning online [23] and good anti-noise performance [24, 25] of FLS-SVM. Moreover, the FLS-SVM parameters such as penalty factor and kernel parameter are optimized by adaptive genetic algorithm; torque soft-sensing of the alternating current electrical dynamometer is investigated, and the energy consumption during the torque soft measurement and direct measurement phase of a gasoline engine is compared, which provides a significant theoretical basis for the application of this new soft measurement method in the alternating current electrical dynamometer and improvement of its cost, measurement accuracy and energy consumption.
2 Method and model
2.1 Fuzzy least square support vector machine
The basic idea of support vector machine (SVM) is, through the non-linear transformation defined by inner product function, to map the N-dimensional sample space (x1, y1), …, (xN, yN) ∈RN, yi ∈{1, -1} to a high-dimensional feature space, in which a non-linear relationship between the input and output can be found. The principle of non-linear regression of SVM is shown in Figure 1.
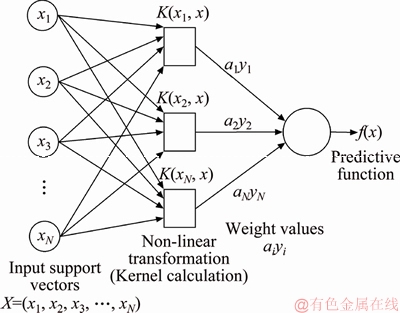
Figure 1 Principle of support vector machine
For the training samples {xi, yi}, where xi (xi∈RN) is the input variable and yi (yi∈R) is the corresponding output value, a non-linear mapping φ(xi) needs to be found out to transform the input variable to a high-dimensional space, in which linear regression is carried out, namely a linear function of the high-dimensional space is configured, as given in Eq. (1):
 (1)
(1)
According to the principle of structural risk minimization (SRM) in statistical learning theory (SLT), the optimization objective of SVM is:
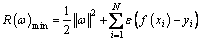
 (2)
(2)
where ε(·) is the loss function.
The basic idea of FLS-SVM is that the inequality constraints in the traditional SVM are transformed into equality constraints and the loss function of error squares sum is taken as the experience loss of the training set; meanwhile, fuzzy theory is introduced into SVM to construct the corresponding objective function and different penalty weight coefficients are used for the samples, making that different samples have different contributions when the objective function is configured, which can weaken the impact of noise and outliers on the classification and improve the solving speed and precision of convergence.
For the given fuzzy sample, similar to the least square support vector machine, a non-linear mapping φ(xi) is introduced to transform the input variable into a high-dimensional space, in which linear regression is carried out and the objective function can be expressed as:
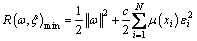
 (3)
(3)
where εi is the slack variable; c is the penalty factor and μ(xi) is the membership of xi.
The Lagrange operator ai (i=1, 2, …, n) is introduced to construct Lagrange equation to solve this optimization problem and the optimization problem of FLS-SVM is converted to the problem of solving the linear Eq. (4):
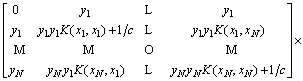
 (4)
(4)
Ultimately, the model of FLS-SVM is as follows:
 (5)
(5)
where K(x, xi) is the Kernel function; K(x, xi)= exp{-|x-xi|2/σ2}; σ is the Kernel parameter.
2.2 Establishment of torque soft-sensing model
2.2.1 Parameter measurement of alternating current electric dynamometer
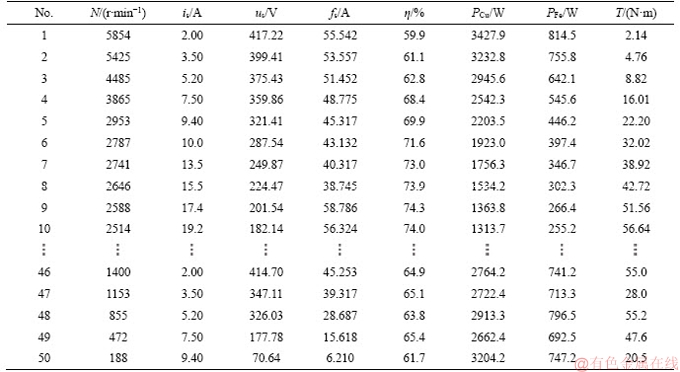
The electric dynamometer test platform is constructed, using alternating current electric dynamometer produced by a power testing instrument Co. Ltd. (Rated power 16 kW, rated speed 2485 r/min, rated torque 70 N·m, maximum speed 8000 r/min), clamp ammeter, 491 electronic fuel injection (EFI) gasoline engine, shaft coupling, FC2450 water and oil temperature control device, etc., and the parameter values of torque T corresponding to 50 groups of different parameters, including rotational speed n, feed network voltage us, feed network current is, feed network frequency fs, efficiency η, copper loss PCu and iron loss PFe, are measured, as shown in Table 1.
2.2.2 Determination of membership function of FLS-SVM
Compared with the traditional SVM, the determination of the membership of FLS-SVM is of great importance. Therefore, to effectively construct the fuzzy membership function becomes a key premise for the establishment of the soft- sensing model on the torque of alternating current electrical dynamometer based on FLS-SVM.
Table 1 Experimental data of alternating current electrodynamometer
In this paper, the method of linear distance is selected to establish the membership function with the main idea that the membership is treated as a linear function of the distance from the sample points in the feature space to the class center; the size of membership is measured based on the distance from the sample to the class center, and the smaller the distance, the greater the membership.
For the sample set {x1, x2, …, xn}, x0 is set as the class center point and r as the radius of the class, then:
 (6)
(6)
 (7)
(7)
Then the membership function of sample can be expressed as:
 (8)
(8)
where δ is a very small constant and greater than 0 to avoid the membership function being 0. Therefore, it can be solved using the objective function shown in Eq. (3) after the membership function of sample is established.
2.2.3 Torque soft-sensing model based on FLS- SVM
In the application process, the torque of alternating current electrical dynamometer has a non-linear relationship with stator voltage, electric current, frequency and loss, as a result of which the measurement on the torque of alternating current electrical dynamometer can be transformed into the measurement on the rotational speed n, feed network voltage us, feed network current is, feed network frequency fs, efficiency η, copper loss PCu and iron loss PFe, and then the torque of alternating current electrical dynamometer can be expressed as the following non-linear equation:
 (9)
(9)
The rotational speed n, feed network voltage us, feed network current is, feed network frequency fs, efficiency η, copper loss PCu and iron loss PFe are taken as the input parameters of the soft-sensing model on the torque of alternating current electrical dynamometer based on FLS-SVM and expressed by a 7-dimensional vector {x1, x2, x3, x4, x5, x6, x7}, then the fuzzy sample training sets of the first 30 groups of input parameters shown in Table 1 can be used for training and the optimal regression function is constructed to obtain the desired regression model for the nonlinear soft sensor on the torque, and its structure is shown in Figure 2.
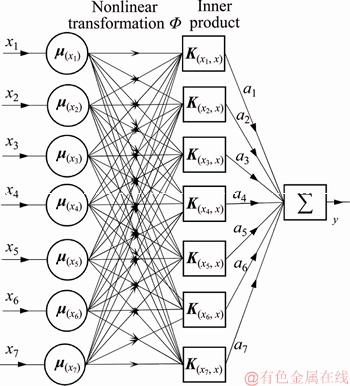
Figure 2 Torque estimating model of alternating current electrical dynamometer
3 Results and discussion
3.1 Optimization of parameters by adaptive genetic algorithm
The penalty factor c and the Kernel parameter σ are the parameters of FLS-SVM which need to be optimized through adaptive genetic algorithm. The value of the penalty factor is set in the range of [1, 500] while that of Kernel parameter is in the range of [0.1, 1], the population number in the process of the adaptive genetic optimization is set as Nind=30 and the number of parameters to be optimized, i.e. the dimension of variable, as Nvar=2; the maximum hereditary algebra is set as Maxgen=300 and binary digit of each variable as Preci=20. Then values are assigned to the initial variables, namely, 0 or 1 is assigned to 30×2×20 binary codes.
Considering that the key to adaptive genetic algorithm is to determine the fitness function, here it is selected as follows:
 (10)
(10)
where yi is the desired output; f(xi) is the actual output; e is a very small positive number, whose role is to prevent the denominator from zero, here e=10-4.
The error function MSE is defined as the evaluation index of the generalization performance of FLS-SVM:
 (11)
(11)
where f(xi) is the actual output and yi is the desired output.
The size of initial crossover probability and mutation probability is determined by Eqs. (12) and (13) respectively:
 (12)
(12)
 (13)
(13)
where f'is the larger fitness function value of two crossover individuals; f is the size of fitness function corresponding to the individual, favg is the average fitness of samples, fmax is the maximum fitness of the sample individuals. The crossover probability and mutation probability change with the evolutionary generation, and the rule is as follows:
 (14)
(14)
 (15)
(15)
where t is the hereditary algebra; tmax is the termination generation; λ is a constant, here λ=10.
The errors corresponding to 30 individuals in the initial species are shown in Figure 3. Figure 4 shows the errors corresponding to 30 individuals after 200 steps of optimization with the average error of 0.1209. Figure 5 shows the errors after 300 steps of iteration with the average error of 0.00657 and the minimum error of about 0.0018.
Compared with the errors of initial species, the errors after 200 steps descend dramatically and the majority of individuals has become saturated.
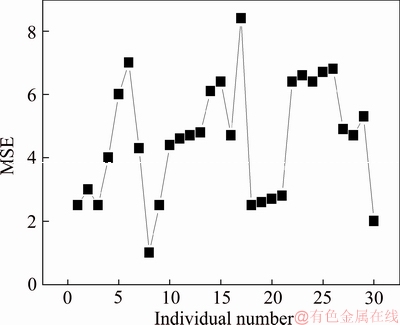
Figure 3 Errors of initial species
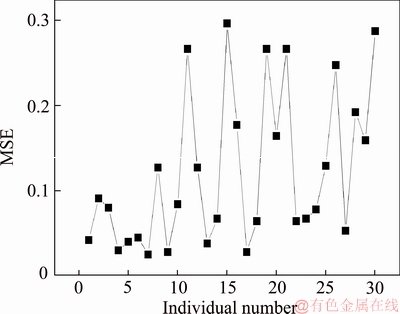
Figure 4 Errors of species after 200 steps of optimization
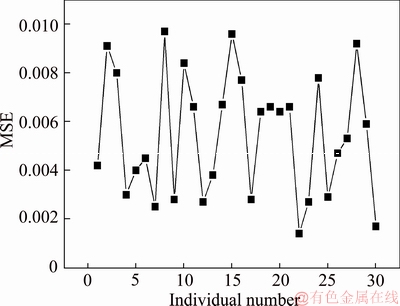
Figure 5 Errors of species after 300 steps of iteration
Ultimately, the optimal value of penalty factor c=58 and Kernel parameter σ=0.8.
3.2 Model verification and comparison
In order to verify the accuracy and practical value of the model established in this paper, fuzzy sample training sets of the latter 20 sets of input parameters shown in Table 1 are adopted for the soft-sensing analysis on the torque of alternating current electrical dynamometer, and the errors between its results and measured values are shown in Figure 6, from which it can be seen that the errors are very small when the FLS-SVM method is applied on estimating the torque of alternating current electrical dynamometer, maintained in the range from -0.3 to 0.3 N·m and achieving high accuracy.
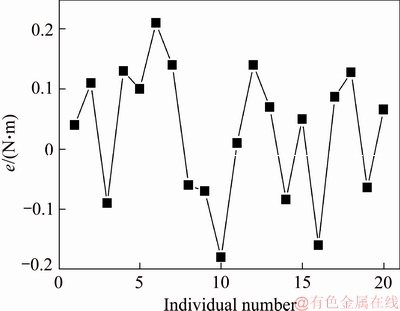
Figure 6 Errors of torque of estimating model
For comparison, in this paper, least square support vector machine is used for the training on the same training sample data and soft-sensing model on the torque of alternating current electrical dynamometer is established, then soft sensor on 10 groups of same test samples is achieved, the results of which are compared with those based on FLS-SVM, as shown in Figure 7.
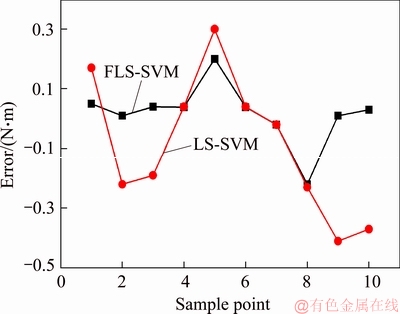
Figure 7 Error comparison of torque soft sensor for alternating current electrical dynamometer
It can be seen from the comparison results of errors shown in Figure 7 that the soft-sensing errors of the soft-sensing model on the torque of alternating current electrical dynamometer based on least square support vector machine fluctuate within a range from -0.5 to 0.4 N·m, significantly higher than the estimation errors obtained from the soft-sensing model on the torque of alternating current electrical dynamometer based on FLS-SVM, mainly because of the stronger anti-noise ability of FLS-SVM, compared with the least square support vector machine, which can assign smaller weight value to the observed samples with noise or wild values and eliminate the impact of noise and wild values on the samples ultimately.
In order to verify effect of the FLS-SVM soft-sensing model on the torque of alternating current electrical dynamometer in the practical application, random 10 sample points are selected from Table 1 and contrasted. The results between direct measurement and indirect estimation are compared in Table 2.
Table 2 Data contrast of direct with indirect measurement
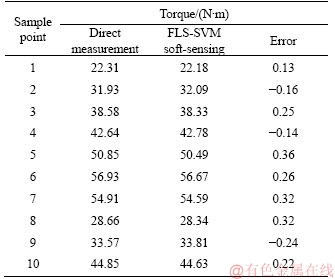
From the contrasting results in Table 2, it can be found that the error of torque between the FLS-SVM soft-sensing values on the torque of alternating current electrical dynamometer and measurement values is quite small. So, the soft-sensing model is of excellent estimating capacity and it is an effective method replacing the direct measurement, satisfying the need of equipments in the practical measurement.
3.3 Torque soft-sensing results of alternating current electrical dynamometer
The reliability of the soft-sensing model on alternating current electrical dynamometer torque is studied, taking the actual operation situation of the mentioned alternating current electrical dynamometer produced by a power testing instrument Co. Ltd. (Rated power 16 kW, rated speed 2485 r/min, rated torque 70 N·m, maximum speed 8000 r/min) for an example. 20 soft sensor readings on the torque of alternating current electrical dynamometer are obtained, using 20 groups of seven parameters including rotational speed n, feed network voltage us, feed network current is, feed network frequency fs, efficiency η, copper loss PCu and iron loss PFe, which are read in 30 min during the operation process, as the input of soft-sensing model on the torque of alternating current electrical dynamometer based on FLS-SVM while corresponding 20 sets of actual torque values of alternating current electrical dynamometer are measured by HN-500 torque test instrument. The changing trend of relative errors is shown in Figure 8.
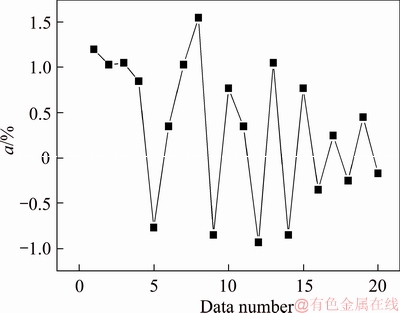
Figure 8 Relative errors between soft-sensing values and actual values of alternating current electrical dynamometer torque
Figure 8 shows that the maximum relative error α between the soft-sensing values and the actual value of alternating current electrical dynamometer torque is less than 2.0%, from which it can be seen that the soft-sensing model on the torque of alternating current electrical dynamometer has pretty high accuracy and is able to achieve the online measurement on the torque of alternating current electrical dynamometer.
Table 3 shows the energy feedback efficiency and energy consumption comparison between the soft-sensing and direct measurement on the torque of alternating current electrical dynamometer. It can be seen that the energy feedback efficiencies of the dynamometer under soft-sensing and direct measurement are 71.8% and 70.2%, respectively, and soft-sensing method can increase by 1.6% power generation feedback compared with direct measurement. Moreover, soft-sensing can save 500 kJ fuel consumption in the gasoline engine loading continual test. Therefore, torque soft- sensing model applied in the alternating current electrical dynamometer has better energy saving effect.
4 Conclusions
1) A soft-sensing model on the torque of alternating current electrical dynamometer is established based on the fuzzy least square support vector machine (FLS-SVM), where rotational speed, feed network voltage, feed network current, feed network frequency and efficiency are employed as input parameters and torque is taken as the output. Then, adaptive genetic algorithm is used for the optimization of the FLS-SVM parameters. The training results show that the corresponding average error is 0.00657 after 300 iteration steps, and the minimum error is about 0.0018; the soft-sensing results show that the soft-sensing errors of the torque soft-sensing model of the alternating current electrical dynamometer based on FLS-SVM fluctuate within a range from -0.3 to 0.3 N·m, which means high prediction accuracy.
2) The torque soft-sensing model of the alternating current electrical dynamometer including copper loss and iron loss is one of effective ways to greatly improve the estimation of accuracy as well as reduce the production cost alternating current electrical dynamometer.
Table 3 Energy feedback efficiency and fuel consumption

Moreover, the measurement error of FLS-SVM soft model is lower than LS-SVM soft model, indicating that FLS-SVM has better ability of anti-noise and removing wild value than the least square support vector machine.
3) FLS-SVM soft-sensing method can increase by 1.6% power generation feedback compared with direct measurement, and it can save 500 kJ fuel consumption in the gasoline engine loading continual test, meaning that torque soft-sensing model applied in the alternating current electrical dynamometer has better energy saving effect.
References
[1] AKPOLAT Z H, ASHER G M, ARELLANO-PADILLA J. A test bed for the experimental validation of position control algorithms [J]. Control Engineering Practice, 2004, 12(8): 933-943. DOI:10.1016/j.conengprac.2003.10.008.
[2] ZHU C L, WANG Y Z, HOU L W. Design and simulation of electrical dynamometer using improved DTC induction motor driver [J]. Journal of Central South University, 2017, 24(6): 1360-1368. DOI: CNKI:SUN:ZNGY.0.2017-06-015.
[3] TOPOLNICKI J, SKOCZYLAS N. Low cost high sensitivity dynamometer [J]. Measurement, 2011, 44(1): 74-79. DOI: 10.1016/j.measurement.2010.09.033.
[4] E J Q, LIU G L, ZHANG Z Q, HAN D D, CHEN J W, WEI K X, GONG J K, YIN Z B. Effect analysis on cold starting performance enhancement of a diesel engine fueled with biodiesel fuel based on an improved thermodynamic model [J]. Applied Energy, 2019, 243: 321-335. DOI: 10.1016/ j.apenergy.2019.03.204.
[5] E J Q, ZHAO X H, QIU L S, ZHANG Z Q, WEI K X, HAN D D, DENG Y W. Experimental investigation on performance and economy characteristics of a diesel engine with variable nozzle turbocharger and its application in urban bus [J]. Energy Conversion and Management, 2019, 193: 149-161. DOI: 10.1016/j.enconman.2019.04.062.
[6] E J Q, ZHAO X H, XIE L F, ZHANG B, CHEN J W, ZUO Q S, HAN D D, HU W Y, ZHANG Z Q. Performance enhancement of microwave assisted regeneration in a wall-flow diesel particulate filter based on field synergy theory [J]. Energy, 2019, 169: 719-729. DOI: 10.1016/ j.energy.2018.12.086.
[7] ZUO Q, ZHU X, LIU Z, ZHANG J, WU G, LI Y. Prediction of the performance and emissions of a spark ignition engine fueled with butanol-gasoline blends based on support vector regression [J]. Environmental Progress & Sustainable Energy, 2019, 38(3): UNSPe13042. DOI: 10.1002/ep.13042.
[8] ZHANG B, E J Q, GONG J, YUAN W, ZUO W, LI Y, FU J. Multidisciplinary design optimization of the diesel particulate filter in the composite regeneration process [J]. Applied Energy, 2016, 181: 14-28. DOI: 10.1016/ j.apenergy.2016.08.051.
[9] WU G, LU Z, PAN W, GUAN Y, LI S, JI C. Experimental demonstration of mitigating self-excited combustion oscillations using an electrical heater [J]. Applied Energy, 2019, 239: 331-342. DOI: 10.1016/j.apenergy.2019.01.133.
[10] YUAN W H, GONG J K, E J Q, YUAN F Q. Fuzzy control strategy for CJD alternating current electrodynamometer [J]. Journal of Xiangtan University: Natural Science, 2006, 28(2): 103-106. DOI: 10.1016/ S1872-1508(06)60066-1. (in Chinese)
[11] KULJANIC E, SORTINO M, TOTIS G. Multisensor approaches for chatter detection in milling [J]. Journal of Sound and Vibration, 2008, 312(4, 5): 20 672-693. DOI: 10.1016/j.jsv.2007.11.006.
[12] WOO L Y, GLASS R S, NOVAK R F, VISSER J H. Diesel engine dynamometer testing of impedancemetric NOx sensors [J]. Sensors and Actuators B: Chemical, 2011, 157(1): 115-121. DOI: 10.1016/j.snb.2011.03.034.
[13] LI Y, TANG W, CHEN Y, LIU J, LEE C F. Potential of acetone-butanol-ethanol (ABE) as a biofuel [J]. Fuel, 2019, 242: 673-686. DOI: 10.1016/j.fuel.2019.01.063.
[14] WU G, LU Z, XU X, PAN W, WU W, LI J, CI J. Numerical investigation of aeroacoustics damping performance of a Helmholtz resonator: Effects of geometry, grazing and bias flow [J]. Aerospace Science and Technology, 2019, 86: 191-203. DOI: 10.1016/j.ast.2019.01.007.
[15] ZHAO X H, E J Q, WU G, DENG Y W, HAN D D, ZHANG B, ZHANG Z Q. A review of studies using graphenes in energy conversion, energy storage and heat transfer development [J]. Energy Conversion and Management, 2019, 184: 581-599. DOI: 10.1016/j.enconman.2019.01.092.
[16] ZUO H Y, LIU G L, E J Q, ZUO W, WEI K X, HU W Y, TAN J Q, ZHONG D Q. Catastrophic analysis on the stability of a large dish solar thermal power generation system with wind-induced vibration [J]. Solar Energy, 2019, 183: 40-49. DOI: 10.1016/j.solener.2019.03.003.
[17] E J Q, LIU G L, LIU T, ZHANG Z Q, ZUO H Y, HU W Y, WEI K X. Harmonic response analysis of a large dish solar thermal power generation system with wind-induced vibration [J]. Solar Energy, 2019, 181: 116-129. DOI: 10.1016/j.solener.2019.01.089.
[18] E J Q, LI Y Q, GONG J K. Function chain neural network prediction on heat transfer performance of oscillating heat pipe based on grey relational analysis [J]. Journal of Central South University of Technology, 2011, 18(5): 1733-1737. DOI: 10.1007/s11771-011-0895-z.
[19] ZUO H Y, LUO Z Q, GUAN J L, WANG Y W. Identification on rock and soil parameters for vibration drilling rock in metal mine based on fuzzy least square support vector machine [J]. Journal of Central South University, 2014, 21(3): 1085-1090. DOI: 10.1007/s11771- 014-2040-2.
[20] WANG T S, ZUO H Y. Fuzzy least squares support vector machines soft measurement model based on adaptive mutative scale chaos immune algorithm [J]. Journal of Central South University, 2014, 21(2): 593-599. DOI: 10.1007/s11771-014-1978-4.
[21] E J Q, QIAN C, ZHU H, PENG Q G, ZUO W, LIU G L. Parameter-identification investigations on the hysteretic Preisach model improved by the fuzzy least square support vector machine based on adaptive variable chaos immune algorithm [J]. Journal of Low Frequency Noise, Vibration and Active Control, 2017, 36(3): 227-242. DOI: 10.1177/0263092317719634.
[22] HAO Z, ZHAO H L, ZHANG C, WANG H, JIANG Y Z, YI Z Y. Estimating winter wheat area based on an SVM and the variable fuzzy set method [J]. Remote Sensing Letters, 2019, 10(4): 343-352. DOI: 10.1080/2150704X.2018.1552811.
[23] ROY A, LASKAR R H. Fuzzy SVM based fuzzy adaptive filter for denoising impulse noise from color images [J]. Multimedia Tools and Applications, 2019, 78(2): 1785-1804. DOI: 10.1007/s11042-018-6303-z.
[24] MANOHAR L, GANESAN K. Diagnosis of schizophrenia disorder in MR brain images using multi-objective BPSO based feature selection with fuzzy SVM [J]. Journal of Medical and Biological Engineering, 2018, 38(6): 917-932. DOI: 10.1007/s40846-017-0355-9.
[25] ZHOU X L, JIANG P Y, WANG X X. Recognition of control chart patterns using fuzzy SVM with a hybrid kernel function [J]. Journal of Intelligent Manufacturing, 2018, 29(1): 51-67. DOI: 10.1007/s10845-015-1089-6.
(Edited by YANG Hua)
中文导读
含铜损和铁损交流电力测功机的扭矩软测量模型
摘要:交流电力测功机是测量发动机转矩的常用仪器设备。针对交流电力测功机扭矩直接测量中存在的问题,如成本高、能耗高、测量系统复杂等,以铜损和铁损为两个主要因素,利用模糊最小二乘支持向量机(FLS-SVM)建立了交流电力测功机的扭矩软测量模型。然后,采用自适应遗传算法对FLS-SVM的惩罚因子和核参数进行优化,将扭矩软测量模型应用于交流电力测功机中,并与其他软测量模型和直接测量进行比较和分析,得到了汽油机连续负载试验测量阶段的能量反馈效率和能耗。结果表明,FLS-SVM软测量扭矩的最小软测量误差约为0.0018,在-0.3~0.3 N·m范围内波动,比直接测量法提高了1.6%的能量反馈效率,并在汽油机连续负载试验中节省了500 kJ的油耗。因此,含铜损、铁损的交流电力测功机扭矩软测量模型的测量精度较高,这种间接测量方法可替代直接扭矩测量方法,并降低交流电力测功机的生产成本和能耗。
关键词:扭矩;模糊理论;最小二乘支持向量机;交流电力测功机
Foundation item: Project(11772126) supported by the National Natural Science Foundation of China
Received date: 2019-05-05; Accepted date: 2019-07-06
Corresponding author: ZHONG Ding-qing, PhD, Lecturer; Tel: +86-13975259709; E-mail: zhdiqi@126.com; ORCID: 0000-0001- 7506-6686