J. Cent. South Univ. Technol. (2011) 18: 411-419

DOI: 10.1007/s11771-011-0712-8

Experimental and numerical study of fence effects on dust emission into atmosphere from open storage piles

S. TORNO^{1, 2}, J. TORA?O^{1, 2}, M MEN?NDEZ^{1, 2}, M. GENT^{1, 2}, I. ?LVAREZ²

1. Mining and Civil Works Research Group, Oviedo University, 33004 Asturias, Spain;

2. School of Mines, Oviedo University, 33004 Asturias, Spain

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: The results obtained from the research on the behaviour of fences (solid and porous) in the protection against particulated material emission to the atmosphere from open storage piles, are presented. This research was carried out through computational fluid dynamics (CFD) simulation by software Ansys CFX-10.0 in 3D, with K-epsilon being considered in the turbulence model. The efficiency of the use of porous fences as a protection against the wind flow, which interacts with an open storage pile, is shown. The use of these fences (when porosity is ε=30%) allows the reduction of wind flow velocity which interacts with the pile in comparison with the case of no use of fences (when porosity is 100%). In addition, the use of porous fences makes the velocity vortex, which is formed between the solid fence (ε=0%) and the pile, disappear, reducing the particle emission to the atmosphere by 78%.

Key words: open storage pile; air pollution; particle emission; wind erosion; porous fence; computational fluid dynamics

1 Introduction

In the different industrial activities [1] of vessel load-unload in ports, the study of the wind effect on open storage piles is of great importance to know the amount of material which is windblown from their surface.

The amount of eroded material from the pile surface can be very high. As an example for coal and iron minerals, the worldwide port traffic was 1 600 Mt in 2008 [2]. To know the amount of lost material and to take preventive measures have financial interests and repercussions on the health and the environment.

Among the different preventive measures which can be taken in order to avoid the loss of material from the stockpiles by the wind effect (total pile coverage, the use of a mixture of chemical substances and water creating superficial crust, etc.), the artificial fence solution was chosen in this research.

The use of fences, due to its efficiency as an environmental pollution protection in different types of industries, was studied by wind tunnel measurements [4], measurement programmes [5-6] and numerical simulation [7-9].

The analysis of the high velocity wind vortex, which is produced between the environmental protection fence and the open mineral storage pile, is of great importance for the particulated material emission [10-12]. This high velocity vortex produces a velocity increase to the windward side of the pile, which means a greater atmospheric particle emission [13].

In comparison with other factors such as the fence configuration or design, the fence porosity is the factor which has more influence on the wind flow produced between the fence and the open mineral storage pile [14].

Lee and Kim [15-16] measured the mean velocity and turbulence profiles of wind between the fence and the pile for different fence porosities using the “Particle Tracking Velocimitry” tool, determining that a 38.5% porosity is the best, since it causes a low wind velocity between the fence and the pile.

In later studies, Lee et al [17] determined that by placing a porous fence in front of the pile, the threshold friction velocity (when the particle gets to be windblown) increases, compared with the case of no use of fence (ε=100%). A 30% porosity fence is the most effective, since this threshold friction velocity increases twice.

The authors have proceeded investigations on the wind flow structure in different fence models through experimental measurements. For each type of fence, solid fence (ε=0%), porous fence (ε=30%) and no fence (ε=100%), 183 wind velocity measurements with hot-wire anemometer and 60 dust concentration measurements, measuring Total Particle and PM10, were developed.

Some turbulence models used by the authors in other studies [5, 7-8, 12] were included again in these simulations, carried out by 3D CFD (Computational Fluid Dynamics) code ANSYS CFX-10.0 [18-19]. These simulations were validated by the measurement programmes mentioned above, determining that the vortex, which is produced between the fence and the pile, diminishes its velocity when a solid fence is changed for a porous fence (ε=30%).

The obtained and validated results, together with the experiences of EPA (Environmental Protection Agency) and Stunder and Arya [20], have been applied to the real situations of particulated material emission for different types of mineral storage piles, quantitatively demonstrating that the use of fences, solid (ε=0%) and porous (ε=30%), produced less emission of particulated material.

2 Experimental

The experiments were carried out in a prepared zone into Carbonar S.A. installation, with an aspect ratio (W/H) of 3.42 and shape ratio (B/H) of 0.04, and a cone at an angle of 37° and a height of 700 mm. In Fig.1, the model dimensions are shown.

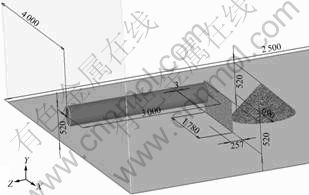
Fig.1 Experimental model sketch carried out by SolidWorks with coordinate system (unit: mm)

In Fig.2, the distribution of the elements used in the experiments, as well as a part of the porous fence used are shown. The fence pores are circular allowing a geometrical porosity (open area percentage) of ε=0%, 30% and 100%.

Fig.2 Distribution of elements used in experiments

The fence is placed at 20.5 cm from the tube which carries the air impulsed by a 12 kW fan, and the cone is at 20.5 cm from the fence (Fig.1). The air provided by the fan can be considered a plane air profile, of about 12.5 m/s, according to the curve-shaped input studies by DIEGO et al [13] from the air velocity values at different outlet points of the tube.

Two types of tests, air velocity measurements and dust concentration measurements, were conducted. These experiments last 10 min each and they were repeated five times in order to obtain an average value which is used to validate CFD modelling. The flow measurements were carried out using a hot-wire anemometer (Velocicalc Plus (TSI)) which has also been used by Coleman and Steele [21] and Kim et al [22] and a MiniAir Junior Schiltknecht anemometer, from a point mesh previously chosen. In dust measurements, two dust collectors (E-Sampler, Met One Instruments, Inc., Oregón, USA) measuring two different particle ranges (0.1-65 mm) for total particle and (0.1-10 mm) for PM10 (using a cyclone which blocks the way the particle entrances with a superior size of 10 mm) were used. These dust collectors were placed at 3 m from the pile.

Concentration data (in mg/m³), were stored in the dust collector memory every minute during the experiments, in which ultrafine coal (0.1-100 mm) was used. This range of particles was determined by Coulter analysis (Particle Size Analyzer) in the INCAR (National Coal Institute belonging to the CSIC-Spanish Council for Scientific Research), from the samples collected during the tests.

Meteorological conditions, relative humidity of atmosphere, temperature, wind velocity and wind direction were also stored each minute by a meteorological station (E-Sampler, Met One Instruments, Inc., Oregón, USA) attached to a PM10 collector. These preliminary experiments were used to validate CFD simulations carried out by software Ansys CFX-10.0. Once the model is validated (geometry and turbulence model), a new model with another geometry, that is, a cone at a height of H=11 m and ratio of 14.59 m with a separation of 22 m from the fence was developed. This fence is 1.2H in height and 3.5H in width [7].

A logarithmic wind profile fixed by EPA determining a velocity of 11.11 m/s at 10 m high location was used in the real model:

                                 (1)

where 0.4 is the constant of von Karman, u is the wind velocity, u* is the friction velocity, z_o is the pile roughness, and z is the height over pile surface.

3 Modelling

3.1 Numerical method

The simulations carried out by software Ansys 10.0, based on 3D computational fluid dynamics, have allowed us to calculate the velocity U(x, y, z) profiles behind the fence. Ansys CFX uses the finite volume method to calculate the Navier-Stokes equations [18] which describe the processes of momentum, heat and mass transfer. This method divides the region of interest into small control volumes, where the Navier-Stokes equations are discretised and solved iteratively.

The continuity equation is

                                    (2)

where r is the density,  is the divergence operator, U is the vector of velocity and t is the time.

The momentum equation is

               (3)

where  is the tensor product, the term  represents the pressure force,  represents the divergence of the stress tensor τ, and S_M is a momentum source term in the generalized form of Darcy’s law.

τ is related to the strain rate by

                              (4)

where m is the molecular (dynamic) viscosity,  is the gradient, T is the temperature and d is the Kronecker delta function (identity matrix).

The total energy equation is

                 (5)

where l is the thermal conductivity, S_E is the energy source and h_tot is the total enthalpy. The term  represents the influence of conduction heat transfer within the fluid, according to the Fourier law of conduction. The term  represents the work due to viscous stresses and is called the viscous work term. The term U?S_M represents the work due to external momentum sources and is currently neglected.

h_tot is related to the static enthalph h(T, p) by

                                                   (6)

were h is the static enthalpy.

Several simplifications can be carried out, such as an incompressible and Newtonian fluid and heat transference.

Within CFD, the software Ansys CFX 10.0 (working by mineral codes) has been chosen to solve this problem.

The pressure difference of the fluid when crossing the fence pores in the simulations is calculated through two coefficients, the linear resistance coefficient (C_R1) and the quadratic resistance coefficient (C_R2). C_R2 has been used to determine the porosity within the software of calculation [23]. By using the Navier-Stokes  equations, these coefficients within the continuous phase calculation are determined. Navier-Stokes equations discretitations produce a series of partial differential equations, which describe the flow properties (momentum and continuity equations):

                              (7)

        (8)

where ?u_i/?t is the acceleration term, u_j(?u_i/?x_j) is the advection term, ?p/?x_i is the pressure term, and (?/?x_i)[u(?²u_i/?x_j?x_j)] is the diffusion term.

S_M,i is the source term

                                  (9)

where C_R1 is set to 0 (kg/m³?s) assuming negligible viscous losses in the ambient air flow (?=1.79×10^-5 N?s/m²), and C_R2 is set to 18.45 kg/m⁴ in a 30% porosity (Tiwary et al [22]); u_i is the dimensional velocity component along the three directions (x, y, z).

In the simulations, the wind velocity decrease within the pores of the porous fence is carried out through Darcy’s law:

                                (10)

The second part of the equation corresponds to the fluid velocity term. This equation for high Reynolds numbers, relates to the fluid velocity, pressure and porosity via K_loss (empirical loss coefficient) (C_R2·ε²/ρ).

3.2 Physical model

The geometry and meshing were carried out by two different types of software, SolidWorks and Ansys IcemCFD 10.0, respectively.

The scale model geometry consists of a parallelepiped of 8 m×5 m×24 m which includes a pipe with a length of 3 m and a diameter of 300 mm, the fence and the cone both being at a height of 520 mm from the ground. The model was meshed with a total of 1 107 611 elements which are tetrahedrons. In this model, a finer meshing at 3 m from the pile has been carried out, where dust concentration measurements were taken by the dust collectors during the tests.

A test of mesh-independence was conducted based on three different meshing creations, a coarse mesh  (253 876 elements), a fine mesh (2 041 027 elements) and an intermediate mesh (1 107 611 elements). Based on the obtained results, an intermediate mesh was selected. Once the domain was meshed, the software checked the elements, determining the good quality (when the tetrahedrons have regular shapes, which indicates the top quality of 1) or on the contrary, these tetrahedrons are distorted with irregular shapes (quality of 0). In this study, the mesh has a quality value of 0.35, which is considered to be acceptable for the ICEMCFD support [24].

For a model with a pile geometry of 11 m in height and 29.18 m in diameter, the domain volume is determinated by 110 m×100 m×350 m. This fence is  13.2 m in height, 20 cm in width, 37.64 m in length and at 22 m distance from the pile. Here, the model has a total of 2 000 000 elements (scale factor/max element= 8.75), with a finer meshing area (reaching a 0.39 quality) that coincide with the pile and the fence surfaces. In order to extrapolate the emission calculation methodology from the scale model, the tetra size surrounding the piles is preserved [7].

In Fig.3 and Fig.4, two meshing planes for both models studied (real and scale models), are shown. In Fig.3, the scale model meshing plane is presented according to the quality of each one of the tetrahedron from which they are formed, distinguishing the finer meshing area at 3 m from the pile, where dust concentration measurements were taken by the dust collectors during the tests.

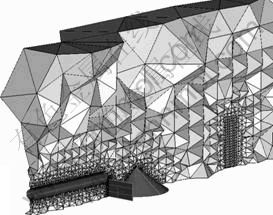
Fig.3 Scale model 3D meshing ( Good quality,  Intermediate quality,  Bad quality)

In Fig.4, the real model meshing plan is shown, presenting the wire frame meshing plane, in which the pile and the fence are included in the finer meshing area. Since the geometry and the meshing have been created, the following step is the physical definition of the model and the characterization of the boundary conditions. In the domain, we have a 25 ?C air affected by gravity, not taking into account of the heat transference which is characterized by the turbulence model K-epsilon. There are different inlets in each model. In the first one (scale model), the inlet is a plane profile with a 12.5 m/s wind velocity, which coincides with the fan air outlet, and in the second one (real model) the inlet is a logarithmic wind profile. The pile and the fence are considered as walls in both models.

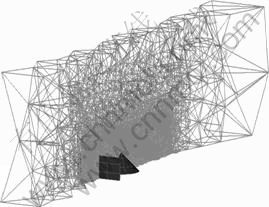
Fig.4 Real model 3D meshing

The absolute porosity introduction in the software Ansys CFX was carried out according to the quadratic resistance coefficient C_R2, as Tiwary et al [24] did.

A set of studies to achieve a relation between this coefficient C_R2 and the absolute porosity value have been carried out. The same velocity vortex measurements behind the pile have been compared with their simulations and with those carried out by Wang and Take [26], determining a good correlation (R²=0.999 7) between the absolute porosity and the quadratic resistance coefficient C_R2:

                                               (11)

4 Wind results

Wind results were performed with a 11 m-high pile and three types of fences were considered (no fence (ε= 100%), solid fence (ε=0%) and porous fence (ε=30%)). Firstly, the scale model results are validated with the experimental measurements, and secondly, the calculation methodology was extrapolated to the real model.

In Fig.5, the mathematical relation between the experimental measurements and those obtained through the Ansys CFX software and the corresponding correlation coefficient are shown for the mean velocities of air in different points.

In the no fence model (ε=100%) (Fig.5(a)), the coefficient R² is 0.928 6; in a solid fence (ε=0%) R² is 0.849 3 (Fig.5(b)), and in a porous fence (ε=30%) R² is 0.885 9 (Fig.5(c)).

Fig.5 Experimental and simulation values comparison for same mean velocity measurement point: (a) No fence (ε=100%);   (b) Solid fence (ε=0%); (c) Porous fence (ε=30%)

In the three studied models, the high correlation coefficient values (R²) show a good adjustment between the experimental data and numerical data of the model, which indicates that, the K-epsilon turbulence model used in this research work is considered the most suitable.

The obtained results give us the extrapolation to other models similar to the reality, that is to say, a logarithmic wind profile to inlet and a geometry of 11 m in height for the pile and 13.2 m in height for the fence.

For the case of no fence (ε=100%), the wind interacts directly with the pile forming behind it a velocity vortex or a recirculating flow, which has been also verified by the results obtained by LEE and LIM [11].

In Fig.6, the mean velocity profiles, at different distances to the cone according to H, H being the pile height and 0H the cone vertex are shown. The size of vectors is according to the value of the mean wind velocity in each study point. As it can be observed in this figure, the vectors increase the velocity on windward surface of the pile, giving place to a wind recirculation which disappears just behind the pile, and the logarithmic wind profile is reestablished at a distance of approximately 8H.

Fig.6 Mean velocity vectors in no fence model (ε=100%)

This necessary distance, in order to reestablish the flow, depends on the pile slope. Kim et al [22] established that a vortex behind the pile was not produced in a 0.3 pile slope, but it did appear in 0.5 pile slope. Besides, it was demonstrated that according to the inclination of the obstacle, the vortex increases in size by decay-law which has been developed by Arya et al [27], where the maximum mean-velocity perturbation is [-(ΔU)_max/U_ref=m(x/H)-1] depending on m, which is a constant that varies according to the shape of obstacle.

The obstacle geometry is one of the factors that have more influence on the wind vortex shape and size behind the pile. Research carried out by Tora?o et al [12] and Diego et al [8] shows how in other types of piles, such as the flat top oval pile and the semicircular pile, the vortex reaches a bigger size at a further distance from the pile base than for the conical pile.

In order to prove that the velocity vortex behind the fence increases as the cone slope increases, the distribution of velocities in a cone of 11 m high at a 79° angle was studied (Fig.7). When modelling a 37° angle cone, it is observed that the recovery zone of the wind flow velocity is smaller, 9H becoming 8H.

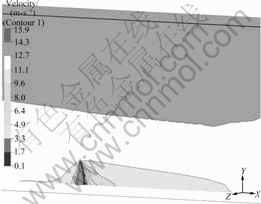
Fig.7 Contour of wind velocity in 79° cone model

The choice of these slope angles is based on former research by Tora?o et al [12], Tora?o et al [7], Torno et al [5], Torno [3] and Diego et al [8], in which they determined that for the use of standard EPA emission formulas [29], a 0.2 relation between the radio and the pile height was necessary. This relation has been used by Stunder and Arya [20] which is the same as the one used in our studies, (11 m high and 37° angle). If this 0.2 relation is not attained, as in the 79° cone model, other special emission formulae will have to be used.

The negative velocity values which define the vortex in the leeward side of the pile can be specified by variable V:

                                                            (12)

where v_m is the mean wind velocity, v_u is the X direction wind velocity given by the program for each calculation point, and v is the reference velocity of logarithmic wind profile.

In Fig.8, the variable V distribution in each line (shown in Fig.6) according to the distance from the cone and a small vortex in the windward side of the pile in the lines placed at -1H, are shown. For the lines placed at 0.5H and 1H, the large vortex which is produced behind the pile is shown.

Fig.8 V values in each of 12 study lines

If a 0% porous fence is set in front of the pile, the logarithmic wind profile interacting with it is modified, forming a recirculation region behind the fence over the pile. The effect of this type of fence is strongly influenced by the fence height, the fence and its distance from the pile, since these parameters determine the vortex dimensions, and also, the particle emission to the atmosphere.

In Fig.9, the vector plane of mean velocity of wind and the vortex produced behind the solid fence (ε=0%) placed at a 2H distance from the pile, are shown.

Fig.9 Velocity vectors in solid fence model (ε=0%)

When a porous fence (ε=30%) is installed in front of the pile, the wind flow that goes through this fence is strongly reduced and interacts with the cone with a lower velocity causing the disappearance of the vortex placed on the windward side of the pile and reducing the recirculation zone, which is produced on the leeward side of the pile (Fig.10).

If the velocity vectors in the two types of fences are compared (Fig.9 and Fig.10), it can be seen that a velocity of 7.5 m/s is reached behind the solid fence (ε=0%), descending to 3.5 m/s when changing to a porous fence (ε=30%) in the same study area. In the no fence model (ε=100%), the velocity, with which the wind flow interacts with the pile, is the greatest in these three models, 8-9 m/s. Besides, the shear layer separation, in a porous fence (ε=30%), is not produced in the cone vertex, as occurred in the no fence model (ε=100%), having lower velocity in this area.

Fig.10 Velocity vectors in solid fence model (ε=30%)

5 Multiphase results

5.1 Introduction

The 4D multiphase modelling is close to what occurs in industry, as particles were added to latter experiments carried out only with wind (monophase modelling). This is achieved through “Particle Tracking” included in software Ansys CFX. This is a Lagrangian solver which allows to simulate particle track along previously calculated velocity fields. Thus, the amount of windblown dust in a mineral pile and its distribution over the pile surface are calculated.

This methodology is very useful, since it allows to improve the storing park design and to apply different alternatives to reduce harmful emissions, for example, by using fences.

The Lagrangian method describes the movements of individual particles as a time function. The following vectors are considered in each particle:

Millions of real windblown particles are represented by software Ansys CFX from thousands of representative tracks with a certain mass quantity. This is named particle number rate (PNR), which is characterized by a one-way coupling, that is to say, the flow is not affected by the particles. Therefore, these particles follow the streamlines [28]:

                                    (13)

where R_p is the particle number rate, s^-1; R_F is the mass flow rate, kg/s; N_p is the number of positions; m_p is the mass of the particle, kg.

Mass of each particle is defined by EPA, which assigns a mass quantity depending on the area from which it is emitted over the pile surface, to each particle. The pile surface is subdivided into small subareas according to u_s/u_r [20]. In each of these subareas, the erosion potential (φ) of the EPA which specifies the emission factor (F_E) is calculated:

                               (14)

                                                                     (15)

where the friction velocity (u*) is determined by software, the threshold friction velocity  is 1 m/s (uncrusted coal pile), particle size multiplier (K) is 0.5 (particles <10 m) [29] and N is 12 disturbances per year.

The latter velocity numerical calculations carried out, are measured at a homogenous height over a 18 cm pile surface, according to the research determined by Muleski [30].

All these terms are compiled by FORTRAN creating routines which are attached to software Ansys CFX through CFD-CCL code on the MS-Dos screen. In Fig.11, a part of the routine used in the dust emission programming is shown.

Fig.11 Injection routines compiled by FORTRAN

In this way, the amount of windblown particles determined by wind velocity maps of the pile surface is emitted.

5.2 Concentration calculation

In the wind study, tests with different materials (limestone, coal and cement) to determine the dust concentration produced at 3 m from the pile, where dust collectors were set, were carried out. During the tests, the dust collectors measured PM10 particles, which are smaller than 10 mm and total particle of 0.1-55 mm.

In Fig.12, concentration-time curves obtained by dust collectors during the experiments are shown in the three types of fences studied.

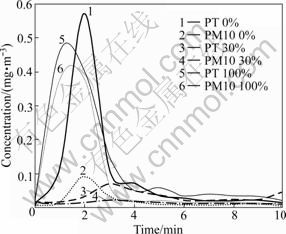
Fig.12 Sensitivity of concentration over test time in three fence types (ε=30%, 0% and 100%)

These curves are the average results of all the tests carried out, distinguishing in all cases the depletion rate curve of the material, that is to say, in 2-3 min there is a high emission, reaching the concentration peak, finally dropping to the reference value.

The authors have used the corresponding latter curves (Fig.12) for particles of smaller sizes than 10 mm, which, in health view, is the most important, as these are susceptible particles to be inhaled by humans around or close to the pile.

In order to validate the numerical models, it has been necessary to compare them with the concentration values obtained in the experiments (Fig.12). Since the numerical data depend on EPA formulations (steady state calculations), and the dust emission follows the depletion rate curve of the material during the test (transient calculations), the adjustment calculations in the area below the PM10 graphic curve, should be carried out. This would be the value to be compared with the obtained software data.

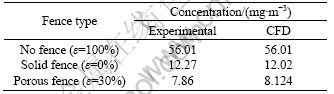
In Table 1, the experimental concentration results and the ones from CFD simulation, are listed. It can be seen that these results are almost equal, thus, our scale simulations are validated.

Table 1 Comparison between CFD and experimental concentration

The clearest difference in the three studied models lies in the dust cloud evolution (Fig.13). It is shown how the dust cloud is reduced in a lower porosity fence (ε=30% and 0%) in relation to no fence model (ε=100%).

With regard to solid fence (ε=0%), a vortex, which traps the particles between the fence and the pile, is produced. This vortex disappears in the porous fence model (ε=30%).

5.3 Emission calculation

In Table 2, the emission ratios obtained by different models are listed. These values follow the same tendency as the velocity and the concentration. There is high emission in no fence model (ε=100%), a strong reduction in the solid fence model (ε=0%) and even a stronger reduction in the porous fence model (ε=30%), which is the best against particle emission to the atmosphere.

Table 2 Dust emission ratio in three fence types

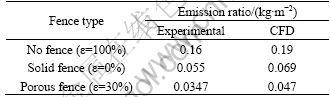
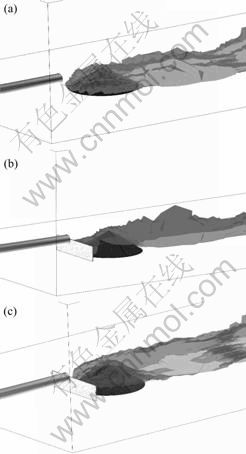
Fig.13 Dust cloud in three models: (a) No fence (ε=100%);   (b) Solid fence (ε=0%); (c) Porous fence (ε=30%)

6 Conclusions

1) In order to diminish the particulated material emission to the atmosphere in open mineral storage piles, the use of artificial fences is one of the best methods. The effect caused by a fence setting is explained. Three fences with three different porosities ε=0%, 30% and 100%, at the distance of 2H from the pile (H being the pile height), are studied.

2) This effect gives a different distribution of wind velocity on the pile surface. Therefore, this distribution of wind emits a particulated material to the atmosphere, depending on the type of porous fence chosen. This research is defined through CFD simulation carried out by software Ansys CFD and validated by experimental tests.

3) When there is no fence, the porosity is ε=100% and the wind is not interrupted. Therefore, it reaches the pile with a high velocity, leading to a higher emission. If a solid fence (ε=0%) is introduced, the wind flow is strongly distorted, causing a flow recirculation behind the fence. This flow distortion produces a velocity decrease over the pile surface, so a lower particle emission is produced.

4) The use of porous fences (ε=30%) allows the reduction of wind flow velocity which interacts with the pile in comparison with the case of no use of fences (ε=100%). In addition, the use of porous fences makes the velocity vortex, which is formed between the solid fence (ε=0%) and the pile, disappear, reducing the particle emission to the atmosphere by 78%.

Acknowledgements

The authors would like to thank the Spanish Ministry of Science and Education that granted these researches through the project CTM2005-00187/TECNO “Prediction Models and Prevention Systems in the Particle Atmospheric Pollution in an Industrial Environment” carried out at Oviedo University.

We are also very grateful for the CFX Users’ support and their contribution.

We would also like to thank Carbonar S. A. Company for the installation disposal in order to carry out the experimental tests.

References

[1] Oravisj?rvi K, Timonen K L, Wiikinkoski T, Ruuskanen A R, Heinanen K, Ruuskanen J. Source contributions to PM2,5 particles in the urban air of a town situated close to a steel works [J]. Atmospheric Environment, 2003, 37(8): 1013-1022.

[2] Port Traffic Stadistics [EB/OL]. http://www.puertos.es/en/ estadisticas/index.html. 2008.

[3] Torno S. Dust emission in open storage piles [D]. Oviedo University, Ed. Ediuno, 2008: 1-382. (in Spanish)

[4] Billman B J, Arya S P S. Windbreak effectiveness for storage-pile fugitive dust control: A wind tunnel study, EPA/600/ S3-85/059 [R]. United Stated Environmental Protection Agency, Research and Development, 1985.

[5] Torno S, Tora?o J, Diego I, Menéndez M, Gent M, Velasco J. CFD simulation with multiphase flows in porous media and open mineral storage pile [J]. WIT Transactions on Engineering Sciences, 2009, 63: 421-430.

[6] Boldes U, Goldberg A, Di Leo J M, Colman J, Scarabino A. Canopy flow and aspects of the response of plants protected by herbaceous shelterbelts and wood fences [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 1253-1270.

[7] Tora?o J, Torno S, Menéndez M, Gent M. Dust emission calculations in open storage piles protected by means of barriers, CFD and experimental tests [J]. Environmental Fluid Mechanics, 2009, 9: 493-507.

[8] Diego I, Pelegry A, Torno S, Tora?o J, Menendez M. Simultaneous CFD evaluation of wind flow and dust emission in open storage piles [J]. Applied Mathematical Modelling, 2009, 33: 3197-3207.

[9] Wilson J D. Numerical studies of flow through a windbreak [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1985, 21: 119-154.

[10] Kim H B, Lee S J. The structure of turbulent shear flow around a two-dimensional porous fence having a bottom gap [J]. Journal of Fluids and Structures, 2002, 16(3): 317-329.

[11] Lee S J, Lim H C. A numerical study on flow around a triangular prism located behind a porous fence [J]. Fluid Dynamics Research, 2001, 28: 209-221.

[12] Tora?o J, Rodríguez R, Diego I, Rivas J M, Pelegry A. Influence of the pile shape on wind erosion CFD emission simulation [J]. Applied Mathematical Modelling, 2007, 31: 2487-2502.

[13] Diego I, Tora?o J, Torno S, García B. Experimental tests and computational fluid dynamics (CFD) simulations of barriers installed around open storage piles of raw materials [J]. WIT Transactions on Engineering Sciences, 2008, 59: 101-109.

[14] Perera MDAES. Shelter behind two-dimensional solid and porous fence [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 8: 93-104.

[15] Lee S J, Kim H B. Laboratory measurements of velocity and turbulence field behind porous fences [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 80: 311-326.

[16] Kim H B, Lee S J. Hole diameter effect on flow characteristics of wake behind porous fences having the same porosity [J]. Fluid Dynamics Research, 2001, 28: 449-464.

[17] Lee S J, Park K C, Park C W. Wind tunnel observations about the shelter effect of porous fences on the sand particle movements [J]. Atmospheric Environment, 2002, 36: 1453-1463.

[18] ANSYS Inc.. ANSYS CFX [EB/OL]. URL: . 2008.

[19] Gosman A D. Developments in CFD for industrial and environmental applications in wind engineering [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 81: 21-39.

[20] Stunder B, Arya S. Windbreak effectiveness for storage pile fugitive dust control: A wind tunnel study [J]. Journal of Air Pollution Control Association, 1988, 38: 135-143.

[21] Coleman H W, Steele W G. Experimentation and uncertainty analysis for engineers [M]. New York: John Wiley & Sons Inc, 1988.

[22] Kim H G, Lee C M, Lim H C, Kyong N H. An experimental and numerical study on the flow over two-dimensional hills [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 66: 17-33.

[23] ANSYS CFX-Solver [M]. Release 10.0: Theory. Flow in porous media, 2008: 65-67.

[24] Tiwary A, Morvan H P, Colls J J. Modelling the size-dependent collection efficiency of hedgerows for ambient aerosols [J]. Journal of Aerosol Science, 2005, 37: 990-1015.

[25] ANSYS ICEMCFD 10.0 [M]. Tutorial Manual, Tetra Meshing, 2008: 309-310.

[26] Wang H, Takle E S. A numerical simulation of boundary-layer flows near shelterbelts [J]. Boundary-Layer Meteorology, 1995, 75: 141-173.

[27] Arya S P S, Capuano M E, Fagen L C. Some fluid modeling studies of flow and dispersion over two-dimensional low hills [J]. Atmospheric Environment, 1987, 21: 753-764.

[28] ANSYS CFX-Solver [M]. Release 10.0: Particle Transport Theory Lagrangian Tracking Implementation, 2008: 174.

[29] US EPA, Update of Fugitive Dust Emissions Factors In AP-42 Section 11.2-Wind Erosion [R]. MRI No. 8985-K, Midwest Research Institute, Kansas City, MO, 1988.

[30] Muleski G E. Coal Yard Wind Erosion Measurement [R]. Midwest Research Institute, Kansas City, MO, 1985.

(Edited by YANG Bing)

Received date: 2010-08-02; Accepted date: 2010-10-25

Corresponding author: S. TORNO; Tel: +34-985104254; E-mail: tornosusana @uniovi.es