J. Cent. South Univ. Technol. (2007)01-0019-05

DOI: 10.1007/s11771-007-0004-5                

Hot deformation behavior and flow stress model of F40MnV steel

WANG Jin(王 进), CHEN Jun(陈 军), ZHAO Zhen(赵 震), RUAN Xue-yu(阮雪榆)

(National Die and Mold CAD Engineering Research Center, Shanghai Jiaotong University, Shanghai 200030, China)

Abstract: Single hit compression tests were performed at 1 223-1 473 K and strain rate of 0.1-10 s^-1 to study hot deformation behavior and flow stress model of F40MnV steel. The dependence of the peak stress, initial stress, saturation stress, steady state stress and peak stain on Zener-Hollomon parameter were obtained. The mathematical models of dynamic recrystallization fraction and grain size were also obtained. Based on the tested data, the flow stress model of F40MnV steel was established in dynamic recovery region and dynamic recrystallization region, respectively. The results show that the activation energy for dynamic recrystallization is 278.6 kJ/mol by regression analysis. The flow stress model of F40MnV steel is proved to approximate the tested data and suitable for numerical simulation of hot forging.

Key words: microalloyed forging steel; flow stress; dynamic recovery; dynamic recrystallization; Zener-Hollomon parameter

1 Introduction

During hot working, several metallurgical pheno- mena such as work-hardening (WH), dynamic recovery (DRV), and dynamic recrystallization (DRX) occur simultaneously^[1]. Flow stress of steels affected observably by microstructure has a significant effect on the forming load and material flow during hot forming. Many DRX models and flow stress models of C-Mn steels and low carbon microalloyed steels have been developed to support research and production of hot rolling^[2-6], but less attention was paid to hot forging process, especially for microalloyed forging steels.

Microalloyed forging steels are widely being used for machinery structural parts because they result in dramatic energy saving by omitting heat treatment^[7-9]. F40MnV steel is one of the representative microalloyed forging steels, which is used for structure parts of automobile^[10]. The hot deformation behavior of F40MnV steel was studied. Also, the flow stress model of the steel was obtained for subsequent applications such as numerical simulation. First, the characteristic parameters of hot deformation, such as the peak strain (ε_p), peak stress (s_p), initial stress (s₀), saturation stress (s_s) and steady state stress(s_ss), were obtained using compression tests and described as functions of Zener-Hollomon parameter. Then, equations for dynamic recrystallization fraction and grain size were obtained. Finally, the flow stress model of F40MnV steel was determined in dynamic recovery region and dynamic recrystallization region, respectively. The validity of the model was demonstrated by comparing the tested data to with the calculated results.

2 Experimental

F40MnV steel with an initial grain size of about 95 μm was used as the specimens for hot compression test. The steel with the nominal composition (mass fraction) of C 0.39%, Mn 1.4%, Si 0.4%, V 0.08%, Cr 0.07%, Ni 0.07%, N 0.012%, was chosen to be tested in this study. The hot compression specimens with 15 mm in length and 10 mm in radius were machined. Single compression tests were performed on a GLEEBLE 1500 thermomechanical simulator at 1 223-1 473 K and strain rate of 0.1-10 s^-1. Argon was used to protect the specimens from surface oxidation, and graphite was used between the specimens and the compress anvils to reduce the friction. The specimens were quenched after tests immediately. Then, they were sectioned longitudinally for microstructural observations. Sections were polished and then etched in an abluent solution of saturated picric acid for about 7 min. Grain sizes were measured by the linear intercept method according to ASTM standards.

3.1 Analysis of flow stress curves

Fig.1 shows the flow stress cures for F40MnV steel at different temperatures and strain rates. Each curve exhibits a peak and softening to an extensive steady state, which indicates dynamic recrystallization behavior. Dynamic recrystallization occurs only after a critical strain (ε_c) has been exceeded. The critical strain (ε_c) of steels was reported to be lower than the peak strain (ε_p).

Fig.1 Flow stress curves of F40MnV steel at different strain rates

 (a)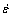=0.1 s^-1;  (b)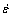=1 s^-1;  (c)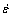=10 s^-1

KIM et al^{[3, 5-6, 11]} estimated the critical strain using the relationship as ε_c=(0.65-0.95)ε_p. Followed the report of SELLARS et al^[12], ε_c=0.83ε_p was employed in this study. Each flow stress curve can be divided into two regions, which are the dynamic recovery region and the dynamic recrystallization region. The dynamic recovery region is the region before the critical strain where dynamic recovery is the predominant softening mechanism. Otherwise, the dynamic recrystallization region is the region after the critical strain where dynamic recovery and dynamic recrystallization act together.

3.2 Analysis of dynamic recrystallization

3.2.1 Activation energy and Zener-Hollomon parameter

The prominent dependence of the flow stress on temperature and strain rate shows that the hot defor- mation process is controlled by thermally activated process. The relationship among these parameters can be expressed by the creep equation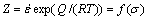^[1]:

       (1)

where  Z is the Zener-Hollomon parameter, Q is the activation energy, R is the gas constant, T is the thermodynamic temperature, and f(σ) is the stress function which can be expressed by the following equation:

f(σ)=A[sinh(ασ)]ⁿ                       (2)

where   A, a, n are the material constants^[13].

To Eqn.(2), the s value is often substituted by s_p. Combining Eqn.(1) and Eqn.(2), there is:

             (3)

When the deformed temperature is constant, the following equation can be gotten by transforming Eqn.(3):

                    (4)

When strain rate is constant, the following equation can be gotten from Eqn.(3):

               (5)

According to Eqns.(4) and (5), n is determined from the relationship between stress term and strain rate in Fig.2, and Q is then calculated from the relationship between stress and temperature in Fig.3. In this study, the n and Q are determined as 3.98 and 278.6 kJ/mol, respectively.

3.2.2 Dependence of characteristic parameters on Z parameter

The characteristic parameters, such as the peak stress (s_p), initial stress (s₀), saturation stress (s_s), steady state stress (s_ss) and peak strain (e_p), are determined from flow curves by the method that MCQUEEN et al^{[11, 14]} employed. The relationship curves between strain hard rate(θ=dσ/dε) and stress are used for determining s_p, s_s and s_ss, and the  curves are employed to determine e_p.

The dependences of s_p and e_p on Z parameter are fitted from the relationship between Z and s_p in Fig.4, and e_p in Fig.5. The same method is used to determine the dependence of other characteristic parameters on Z parameter.

Fig.2 Relationship between peak stress and strain rate 

Fig.3 Relationship between peak stress and temperature

Fig.4 Relationship between Z and peak stress

The dependence of those characteristic parameters on Z parameter are determined as following equations:

σ_p=83.33sinh^-1(0.002 9Z^0.25)          (6)

ε_p=0.017Z^0.123                     (7)

ε_s=83.33sinh^-1(0.004 1Z^0.24)       (8)

Fig.5 Relationship between Z and peak strain

σ_ss=83.33sinh^-1(0.001 2Z^0.28)      (9)

σ₀=0.96Z^0.15                  (10)

3.2.3 Dynamic recrystallization fraction

Dynamic recrystallization fraction can be cxpressed as follows with modified JMAK equation^[12]:

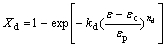  (ε≥ε_c)   (11)

where  X_d is dynamic recrystallization fraction, k_d  and n_d are dynamic recrystallization parameters depending on chemical composition and hot deformation conditions.

To determine the progress of dynamic recrystalli- zation fraction X_d, the following expression is employed^[15]:

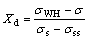   (ε≥ε_c)        (12)

where  σ_WH denotes the flow stress if dynamic recovery is the only softening mechanism and is determined by relationships between strain hardening rate (θ) and  stress (σ).

From Eqn.(12), the amount of DRX is determined by means of the flow stress curves under different deformation conditions. Combining Eqn.(11) and Eqn.(12), k_d and n_d are determined. Fig.6 shows the dependence of k_d on the Z parameter, from which, Eqn.(13) is determined. n_d for the tested steel seems to approach a constant and equals to 1.7.

k_d=2.8×10^-4Z^0.29                  (13)

3.2.4 Dynamic recrystallization grain size

The dynamic recrystallization grain size depends on the deformation temperature and strain rate, which is a function of Z parameter alone and independent of the initial grain size^[12]. Fig.7 shows that the dynamic recrystallization grain size (D_dyn) decreases with increasing strain rate and decreasing temperature. The dependence of D_dyn on Z parameter is determined as the following equation from Fig.8:

D_dyn=3 771Z^-0.2                 (14)

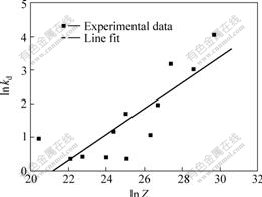
Fig.6 Relationship between Z and k_d

Fig.7 Dynamic recrystallization grains after compression tests

(a)      T=1 473 K,=0.1 s^-1;  (b) T=1 473 K,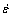=10 s^-1; (c) T=1 273 K,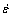=10 s^-1

Fig.8 Relationship between dynamic recrystallization grain size and Z

3.3 Flow stress model

ESTRIN et al^[16] derived the variation of dislocation density during deformation according to work hardening and dynamic recovery as the following equation^[2]:

             (15)

where  U denotes the work hardening and Ω accounts for dynamic recovery during deformation.

Assuming U and Ω are independent of strain and using the classic relationship between stress and dislocation density^[17], σ_WH=αGbρ^0.5, Eqn.(15) can be solved. The resulting relation can be expressed by the following equation:

  (ε＜ε_c)  (16)

where  Ω is determined as the following equation by the method of Laasraoui^[1].

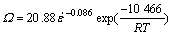     (17)

To model softening due to dynamic recrystallization, Eqns.(11) and (12) are combined and rewritten as following to obtain the flow stress model in the dynamic recrystallization region(ε≥ε_c):

(ε≥ε_c)  (18)

Fig.9 shows comparison of flow stress curves predicted by the model and experimentally measured data at isothermal condition and constant strain. It shows good agreement between two sets of data.

Fig.9 Calculated and experimental flow stress curves

(a)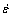＝0.1 s^-1; (b)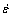＝1 s^-1

4 Conclusions

1) The activation energy of F40MnV steel is 278.6 kJ/mol. The relationships between the characteristic parameters, such as peak stress(s_p), initial stress(s₀), saturation stress (s_s), steady state stress(s_ss) and peak stain (e_p), and Z parameter are determined.

2) The dynamic recrystallization fraction (X_d) and grain size (D_dyn) of F40MnV steel can be expressed as: and D_dyn=3 771Z^-0.2, respectively.

3) The flow stress model of F40MnV steel is obtained in the dynamic recovery region and the dynamic recrystallization region, respectively, which is proved to predict experimental data well.

References

[1] LAASRAOUI A, JONAS J J. Prediction of steel flow stresses at high temperatures and strain rates[J]. Metallurgical Transactions A, 1991, 22A(7): 1545-1558.

[2] SERAJZADEH S, KARIMI T A. Prediction of flow stress at hot working condition[J]. Mechanics Research Communications, 2003, 30(1): 87-93.

[3] KIM S I, LEE Y, BYON S M. Study on constitutive relation of AISI 4140 steel subject to large strain at elevated temperatures[J]. Journal of Materials Processing Technology, 2003, 140(1/3): 84-89.

[4] SERAJZADEH S, KARIMI T A. An investigation on the effect of carbon and silicon on flow behavior of steel[J]. Materials and Design, 2002, 23(3): 271-276.

[5] MEDINA S F, HERNANDEZ C A. Modelling of the dynamic recrystallization of austenite in low alloy and microalloyed steels[J]. Acta Materialia, 1996, 44(1): 165-171.

[6] HERNANDEZ C A, MEDINA S F, RUIZ J. Modelling austenite flow curves in low alloy and microalloyed steels[J]. Acta Materialia, 1996, 44(1):155-163.

[7] NAYLOR D J. Microalloyed forging steels[J]. Materials Science Forum, 1998, 284/286:83-94.

[8] GONZALEZ-BAQUET I, KASPAR R, RICHTER J, et al. Microalloying and a new post forging treatment of medium carbon steels[J]. Materials Science Forum, 1998, 284/286: 411-418.

[9] de ARDO A J. Microalloyed strip steels for the 21st century[J]. Materials Science Forum, 1998, 284/286:15-26.

[10] DONG Cheng-rui, REN Hai-ou, JIN Tong-zhe, et al. Microalloyed Forging Steel[M]. Beijing: Metallurgical Industry Press, 2000.(in Chinese)

[11] MCQUEEN H J, YUE S, RYAN N D, et al. Hot working characteristics of steels in austenitic state[J]. Journal of Materials Processing Technology, 1995, 53(1/2): 293-310.

[12] SELLARS C M, WHITEMAN J A. Recrystallization and grain growth in hot rolling[J]. Metal Science, 1979, 13(3/4):187-194.

[13] KARHAUSEN K, KOPP R. Model for integrated process and microstructure simulation in hot forming[J]. Steel Research, 1992, 63(6): 247-256.

[14] IMBERT C A C, MCQUEEN H J. Dynamic recrystallization of A2 and M2 tool steels[J]. Materials Science and Engineering A, 2001, 313(1/2):104-116.

[15] KONG L X, HODGSON P D, WANG B. Development of constitutive models for metal forming with cyclic strain softening[J]. Journal of Materials Processing Technology, 1999, 89/90: 44-50.

[16] ESTRIN Y, MECKING H. Unified phenomenological description of work harding and creep based on one-parameter models[J]. Acta Metallurgica, 1984, 32(1): 57-70.

[17] MECKING H, KOCKS U F. Kinetics of flow and strain-hardening[J]. Acta Metallurgica, 1981, 29(11): 1865-1875.

(Edited by YANG You-ping)

Foundation item: Project (50275094) supported by the National Natural Science Foundation of China

Received date: 2006-05-08; Accepted date: 2006-07-09

Corresponding author: WANG Jin, Doctoral candidate; Tel: +86-21-62813430-8313; E-mail: jinwang@sjtu.edu.cn