J. Cent. South Univ. (2018) 25: 3021-3032

DOI: https://doi.org/10.1007/s11771-018-3971-9

Effects of initial bubble size on geometric and motion characteristics of bubble released in water

KANG Can(康灿), ZHANG Wei(张伟), ZOU Zi-wen(邹子文), PANG Chun-bo(庞春波)

School of Energy and Power Engineering, Jiangsu University, Zhenjiang 212013, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: To seek and describe the influence of bubble size on geometric and motion characteristics of the bubble, six nozzles with different outlet diameters were selected to inject air into water and to produce different bubble sizes. High-speed photography in conjunction with an in-house bubble image processing code was used. During the evolution of the bubble, bubble shape, traveling trajectory and the variation of bubble velocity were obtained. Bubble sizes acquired varied from 0.25 to 8.69 mm. The results show that after the bubble is separated from the nozzle, bubble shape sequentially experiences ellipsoidal shape, hat shape, mushroom shape and eventually the stable ellipsoidal shape. As the bubble size increases, the oscillation of the bubble surface is intensified. At the stabilization stage of bubble motion, bubble trajectories conform approximately to the sinusoidal function. Meanwhile, with the increase in bubble size, the bubble trajectory tends to be straightened and the influence of the horizontal bubble velocity component on the bubble trajectory attenuates. The present results explain the phenomena related to relatively large bubble size, which extends the existing relationship between the bubble terminal velocity and the equivalent bubble diameter.

Key words: bubble size; nozzle diameter; bubble deformation; aspect ratio; bubble terminal velocity

Cite this article as: KANG Can, ZHANG Wei, ZOU Zi-wen, PANG Chun-bo. Effects of initial bubble size on geometric and motion characteristics of bubble released in water [J]. Journal of Central South University, 2018, 25(12): 3021–3032. DOI: https://doi.org/10.1007/s11771-018-3971-9.

1 Introduction

The enthusiasm for the bubbly flow has never faded during the advancement of fluid dynamics and multiphase flows. Bubble size and its spatial distribution are two key factors that influence bubbly flow patterns [1, 2]. Essentially, the knowledge of the movement of even a single bubble in bubbly flows is insufficient. In this context, multiple factors such as operation condition, liquid property and bubble generation method contribute to the diversity of bubble trajectory, bubble geometry and bubble velocity [3, 4].

The application of computational fluid dynamics (CFD) facilitates the identification and description of bubble deformation and bubbly flow structures [5, 6]. Nevertheless, for large bubbles, numerical models cannot depict the complex interfacial effect between the bubble and surrounding liquid; moreover, the motion of the bubble exposed to turbulent fluctuations is difficult to trace numerically.

Studies on bubbly flows have benefited from the rapid development of flow measurement and visualization techniques. Of significance is the extensive practice using advanced techniques, such as high-speed photography, laser Doppler velocimetry (LDV), particle image velocimetry (PIV), planar laser-induced fluorescence (PLIF) [7, 8]. Bubble shape, trajectory and terminal velocity are interrelated and influenced by the nozzle [9]. Nevertheless, the literature documenting the motion of large bubbles, in particular those with the diameter larger than 3 mm, is not adequate. Furthermore, most existing relationships between bubble parameters are empirical and their feasibility for large bubbles still calls for validation.

Bubble velocity is related to several factors such as liquid property, liquid contamination, bubble size and air injection mode [10, 11]. It was concluded that the contamination of water causes the decrease of the bubble terminal velocity [12]. In Ref. [13], the bubble terminal velocity in the liquid containing inorganic salt was investigated and it was revealed that as the inorganic salt concentration improves, bubble oscillation attenuates, and the bubble terminal velocity decreases. It was proved in Ref. [14] that the bubble velocity in a state of equilibrium varies inversely with equivalent bubble diameter. Nevertheless, in these studies, only those bubbles with diameters less than 2 mm were considered.

The purpose of the present study is to describe the effect of bubble size on bubble shape and bubble motion characteristics. An experiment rig was built to produce bubbles through injecting air into water. Nozzles with different outlet diameters were used. Bubble images were acquired using high-speed photography. An image-processing code was developed to identify bubble profile in the images and to calculate bubble geometric parameters and bubble velocity. A comparison was implemented between bubbles of different sizes. A statistical investigation was performed to correlate the bubble terminal velocity with bubble size.

2 Experimental set-up and image- processing code

2.1 Experimental rig

The experimental system is schematically shown in Figure 1. A rectangular water tank made of plexiglass was used to contain pure water. The tank has identical horizontal cross sections with dimensions of 150 mm×150 mm, and the height of the water tank is 500 mm. At the symmetric center of the bottom wall of the tank, a nozzle was mounted via a ventilation hole. The nozzle was connected to a syringe pump through a plastic tube, and a check valve was used to avoid the backflow of water from the tank to the pump. Another important function of the valve was to change the flow rate of the injected air, q_V, and as a result, the initial bubble size will be changed. The frequency of bubble generation was regulated by adjusting operation parameters of the syringe pump. During the experiment, the water level was kept at 420 mm relative to the bottom wall of the water tank. Six nozzles with the outlet diameter D₀ of 3.00, 2.20, 1.60, 0.60, 0.19 and 0.16 mm, were used in the experiment.

Figure 1 Schematic view of bubble visualization experiment system

Bubble images were recorded using an OLYMPUS I-SPEED 3 high-speed camera, as shown in Figure 1 as well, which was jointly used with an OLYMPUS ILP-2 light source. The light passes through an acrylic diffuser plate of 5 mm in thickness before arriving at the water tank. The acrylic diffuser plate was used to uniformize the incident light over the depth of view (DOV) plane. In consideration of the magnitude of bubble rising velocity, the exposure time of the camera was set to 1 ms.

The rising bubble will reach a state of equilibrium after traveling a vertical distance [15]. For such a distance, a suggestion of 75 mm was presented [16]. In this context, a rectangular coordinates system was defined. The origin of the coordinates system overlapped with the center of the nozzle outlet section. The x-y plane was parallel with the diffuser plate and y points upwards. Two regions, Region A with y ranging from 0 to 112 mm, and Region B with y ranging from 200 to 290 mm, were monitored to capture bubble characteristics at different states and to acquire bubble data for statistical analysis.

2.2 Bubble image processing preparation

To identify the bubble in the image and to extract quantitative bubble information, a code was developed based on the commercial MATLAB software. Bubble image consists of a series of pixels with different grayscale values, serving as the basis for the idea of recognizing and plotting bubble profile in the bubble image. The primary steps of bubble-image processing are shown in Figure 2 [17]. Firstly, the background image was subtracted from the raw image, then the image was processed using image binarization and median filtering approaches, as seen in Figures 2(a) and (b). In Figure 2(c), the color of the cavity surrounded by the bubble profile was inverted. Then the Canny algorithm was used to track the bubble edge, and the result is shown in Figure 2(d).

Figure 2 Procedures of bubble image processing:

Bubble size is an important quantity in describing the characteristics of the bubbly flow [18]. The bubble area A is represented by the combination of the pixels in the filled area shown in Figure 2(c). The circumference was obtained by adding together the pixels constituting the bubble edge. The equivalent bubble diameter, d, is calculated by:

                                (1)

The coordinates of the bubble center, x_c and y_c, are given as:

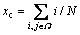,                (2)

where i and j are the abscissa and ordinate of the pixel in the bubble region, respectively; N is the total number of pixels in the area enclosed by the bubble edge; Ω is the set of pixels. The bubble trajectory is described with the time-dependent variation of x_c and y_c. Furthermore, the bubble velocity is given as:

                        (3)

where

                        (4)

and

                       (5)

and the superscript t and t+△t represent two consecutive moments.

During the bubble rising process, four kinds of bubble shapes are typical, as displayed in Figure 3. Bubble shape depends primarily on two factors. One is viscous effect and the other one is surface tension. As viscous effect is dominant, bubbles are spherical or nearly spherical, and bubble surface is stable and short of oscillation. Otherwise, subjected overwhelming to surface tension, bubbles with ellipsoidal, hat or mushroom shapes are common, and bubble wobbling is apparent.

The bubble aspect ratio, E, is used to express bubble shape. E is defined as the ratio of the bubble height to the bubble width:

                                 (6)

2.3 Uncertainty analysis

The uncertainty in the presented work is composed of three constituents, namely the system uncertainty associated with the experiment rig, the uncertainty with bubble size calculation, and the uncertainty entailed by bubble velocity calculation. The components of the experimental rig were fabricated and assembled precisely; therefore, the system uncertainty is negligible. Regarding the imaging processing steps, according to the assessment in Ref. [19], the error with the calculation of equivalent bubble diameter can be quantified with pixels. Here, the attainable spatial resolution of the camera was 0.0879 mm/pixel. The largest bubble diameter was 8.69 mm, which was determined through comparing the bubble diameters obtained through image processing and the physical size of the nozzle. Based on an assumption that the pixel number and bubble size are linearly related, the maximum uncertainty of ±2.78% in bubble size acquisition is deduced. As for the bubble velocity calculation, the uncertainty originates chiefly from the positioning of the centroid of the same bubble in consecutive bubble images, and it is related to bubble profile identification. With a conservative evaluation with the uncertainties considered being combined algebraically, the overall uncertainty in the presented experiment is approximately ±8%.

Figure 3 Typical bubble shapes during bubble rising process:

3 Experimental results and analysis

3.1 Initial bubble shape

The variation of bubble shape immediately downstream of the nozzle is illustrated in Figure 4, where six groups of consecutive images correspond respectively to the six nozzles. The injected air flow rate of 20 mL/h was kept constant for all cases.

Prior to being fully separated from the nozzle, the bubble has a clear bubble tail and a vertically prolonged profile. Then, the bubble oscillates in vertical direction as the physical contact between the bubble and the nozzle is entirely absent [20]. For relatively large bubbles, as shown in Figures 4(a)–(c), vertical oscillation is apparent and the period lasted is long compared with the other cases. During the experiment, it was observed that the vertical oscillation was drastic even in Region B for large bubbles. The bubble images exhibited in Figure 4 contain typical bubble profiles at the initial stage of bubble evolution after the bubble departs from the nozzle. Since the nozzle exerts a boundary effect on the bubble at the moment, it is separated from the nozzle, the lower part of the bubble shrinks and local energy is accumulated. Eventually, the bubble is separated from the nozzle, but the energy in the lower part of the bubble compels it to oscillate vertically. As the bubble rises continuously, the energy leading to bubble oscillation attenuates. Regarding large bubbles, such a process is relatively long. Within this period, bubble shape transforms from ellipsoidal to hat shape, and then the mushroom shape. After several cycles of oscillation, a stable ellipsoidal bubble shape is attained. In contrast, relatively small bubbles shown in Figures 4(d)–(f) undergo relatively slight vertical oscillation. Meanwhile, the duration of bubble deformation is short.

As for large bubbles, with the contribution of surface tension and the influence of ambient water, bubble surface fluctuates violently. In contrast, the spherical shape is attained rapidly for small bubbles as they break away from the nozzle, signifying a balance state of bubble shape evolution.

The bubble aspect ratio is plotted in Figure 5 as a function of evolution time. For the six cases, the overall variation trends of the bubble aspect ratio are similar. With continuous rising of the bubble, the bubble aspect ratio decreases with fluctuations, which is accompanied with the vertical oscillation of the bubble surface.

The aspect ratio of large bubble declines sharply with the evolution of the bubble. From t=0 to 6 ms, for small bubbles, the spherical and hat shapes are predominant, as evidenced in Figure 5. For large bubbles, as shown in Figure 4, they are elongated in vertical direction; then their profiles are flattened. Small bubble secures a small volume and low rising velocity; therefore, both the resistance from ambient water and the surface tension are low. At 6 ,the majority of the bubbles shown in Figure 5 are ellipsoids. In this context, as the bubble velocity increases, the resistance to bubble rising is promoted.Consequently, the bubble velocity is reduced; then the resistance dwindles again.

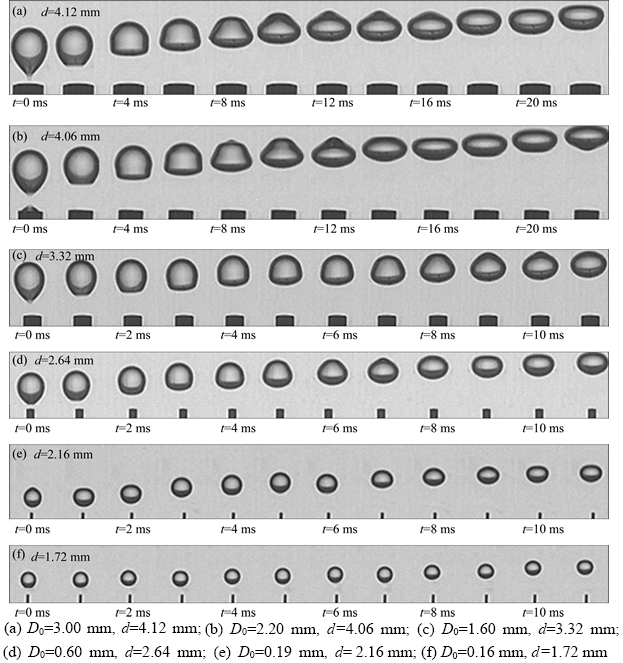
Figure 4 Consecutive bubble images captured with different nozzles at q_V= 20 mL/h:

Figure 5 Variation of bubble aspect ratio as bubble rises

3.2 Bubble trajectory

1) Bubble trajectory in Region A

After the bubble detaches from the nozzle, the buoyant force drives it to ascend in water. Since the DOV plane is two-dimensional, the captured image records the projection of the three-dimensional bubble trajectory onto the DOV plane. In Region A, bubble rising trajectories with the six nozzles are plotted in Figure 6, where the small circles indicate transient bubble positions and the identical time interval between neighboring two positions is 5 ms. The flow rate of the injected air is 20 mL/h, which is shared by all cases in Figure 6.

Figure 6 Bubbles trajectories with different nozzles in Reginon A:

In Region A, variations of the bubble velocity and bubble surface oscillation are remarkable. In Figure 6, near the nozzle outlet, each bubble trajectory covers a linear segment although the length of the linear segment varies. The largest bubble is associated with the longest linear segment length of 79.62 mm, followed by the smallest bubble, as shown in Figures 6(a) and (f). Furthermore, the length of the latter is about half of that of the former. Then the bubble trajectory begins to wobble and the trajectory shown in Figure 6(d) is featured by the most violent horizontal deviation relative to y axis. It is noticeable that the largest bubble rises along a nearly straight route. Overall, the trajectory oscillation of large bubbles is relatively weak.

In Region A, bubble velocity components, V_x, and V_y were obtained through image processing, and the results are plotted in Figure 7. The variation of the bubble aspect ratio is plotted in Figure 7 as well. At this stage, the bubble is in a state of instability, as can be inferred from the fluctuation of velocity curves. For equivalent bubble diameters of 1.72, 2.16 and 2.64 mm, the vertical velocity component increases rapidly near the nozzle. While for the other three equivalent bubble diameters, bubble motion exhibits strong randomness, vertical velocity varies drastically as the bubble progresses and gets stable after several oscillation periods.

It is seen in Figure 7 that the bubble aspect ratio and vertical bubble velocity vary synchronously but in an inverse manner. The crest of the aspect ratio curve corresponds to the trough of the vertical velocity curve, as shown in Figure 7. As the vertical bubble velocity increases, the resistance from ambient water increases simultaneously. Consequently, a high pressure difference between the upper and lower sides of the bubble arises and the bubble surface tends to be flattened and the aspect ratio decreases accordingly. Since the flattened bubble suffers from a large drag force, the increase of the vertical bubble velocity is hindered. These alternate steps boost the bubble oscillation. Regarding large bubbles, there is no consistent relationship between the aspect ratio and the velocity component, as indicated in Figure 7. The variation of the aspect ratio with the bubble rising is severe in Figures 7(a) and (b) relative to that in Figures 7(c) and (f). The aspect ratio in Figure 7(c) is associated with a nearly spherical bubble. Regarding the variation of the horizontal bubble velocity with bubble rising, Figures 7(c) and 6(c) are in good accordance, and small horizontal velocity magnitude is compatible with the nearly linear bubble trajectory.

2) Bubble trajectory in Region B

Bubble trajectories in Region B are displayed in Figure 8. The bubble trajectories in Region B are characterized by periodicity, and all the six trajectories can be approximated with the sinusoidal function. The largest bubble is associated with a fairly straight trajectory, and the smallest bubble is responsible for the longest sinusoidal wavelength. As the equivalent bubble diameter decreases, the sinusoidal wavelength decreases consistently.

Variations in the bubble aspect ratio and bubble velocity in Region B are shown in Figure 9. The bubble aspect ratio varies remarkably for large bubbles. Furthermore, the periodicity of the bubble aspect ratio variation is explicit and differs significantly from the situations shown in Figure 7. In contrast, in Figures 9(e) and (f), bubble deformation is relatively slight. Apparently, the fluctuation of the vertical bubble velocity is suppressed. Moreover, it is seen that the horizontal velocity curves are similar to bubble rising trajectories displayed in Figure 8. Bubbles situated in Region B undergo a stable state with which the bubble motion is dominated by the horizontal bubble velocity. Moreover, in Region B, the disturbance of the fluctuation of the vertical bubble velocity fluctuation to the bubble trajectory is evidently weakened.

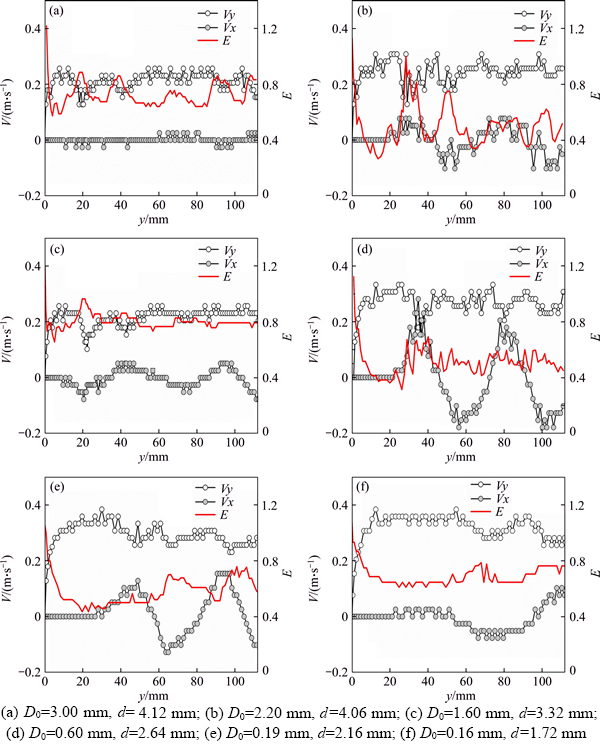
Figure 7 Variation of bubble aspect ratio and velocity components as bubble rises in Region A:

As can be summarized that the rising process of the bubbles considered covers three distinct stages: 1) Vertical bubble velocity dominated stage, at which the vertical bubble velocity varies drastically while the horizontal bubble velocity remains stable, and bubble rises along a fairly straight route; 2) Bubble velocity fluctuation stage, at which the bubble begins to rise in a zigzag pattern, fluctuations of both horizontal and vertical bubble velocities are prevalent; 3) Stable bubble rising stage, at which the bubble trajectory is approximated with the sinusoidal function and the horizontal bubble velocity is predominant. For bubbles with different initial sizes, the time spans for the same stage are significantly different.

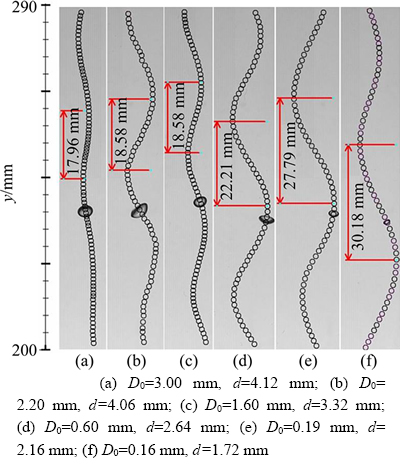
Figure 8 Bubbles trajectories with different nozzles in Region B:

3.3 Influence of air flow rate on bubble geometry

With the same nozzle, the adjustment of the flow rate of injected air triggers the variation in the initial bubble size. Here, the nozzle of D₀=2.20 mm is selected as a representative and bubbles with various equivalent diameters produced thereby are displayed in Figure 10. From Figures 10(a) to (f), q_V increases continuously. The bubble evolution is at the stage dominated by the vertical velocity. A nearly spherical bubble with the equivalent diameter of 1.13 mm is shown in Figure 10(a). As the equivalent diameter increases, the spherical shape is shifted into the ellipsoidal one, as demonstrated in Figures 10(b) and (c). From Figures 10(c) to (d), bubble shape experiences a remarkable change and the ellipsoidal bubble is replaced with a flattened one. Meantime, the bubble oscillation is reinforced. As q_V increases further, the equivalent bubble diameter increases to 8.48 mm, as displayed in Figure 10(f). Such a large size can be produced only in stationary water. For flowing water, it is perceivable that the shear effect outweighs the surface tension of the bubble, and bubble surface integrity cannot sustain.

3.4 Terminal velocity

As the drag and buoyancy forces exerted upon the bubble are entirely counteracted in y direction, vertical bubble velocity no longer changes and the terminal velocity is accomplished. Such a situation signifies an equilibrium state for the rising bubble in stationary water. In this context, the bubble has been completely relieved from the effect of the nozzle. The balance between the drag and buoyancy forces is expressed as:

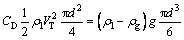              (7)

where C_D is the drag coefficient; the terminal velocity V_T is thus given by:

                       (8)

It was predicted in Ref. [21] that the value of C_D for the distorted bubbles is larger than that of spherical bubbles and therefore the following expressions are recommended for C_D in pure liquid:

 (9)

where Eo is the Etvs number and is defined as:

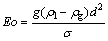                       (10)

In addition to calculating the bubble terminal velocity through C_D, the approach of directly predicting such a velocity was proposed in Ref. [22]. They associated the bubble rising velocity with hydrodynamic principles of waves and the following equation was constructed:

              (11)

The solutions of Eqs. (8) and (11) can be obtained analytically, but the validation has not been attained experimentally for large bubble diameters considered here. As a prerequisite of statistical investigation of bubble geometry and the bubble velocity, bubble data were supplemented in Region B through adjusting the flow rate of the injected air. The bubble terminal velocity and corresponding equivalent bubble diameters were calculated and processed statistically. The result is shown in Figure 11. At 0.25 mm obtained via Eq. (8), but is contrary to Mendelson’s prediction with Eq. (11). In this context, small bubbles are nearly spherical and fluctuate only slightly so that the motion of small bubbles does not conform to the hydrodynamic wave theory. Therefore, Eq. (11) is only suitable for conditions of medium-sized bubbles.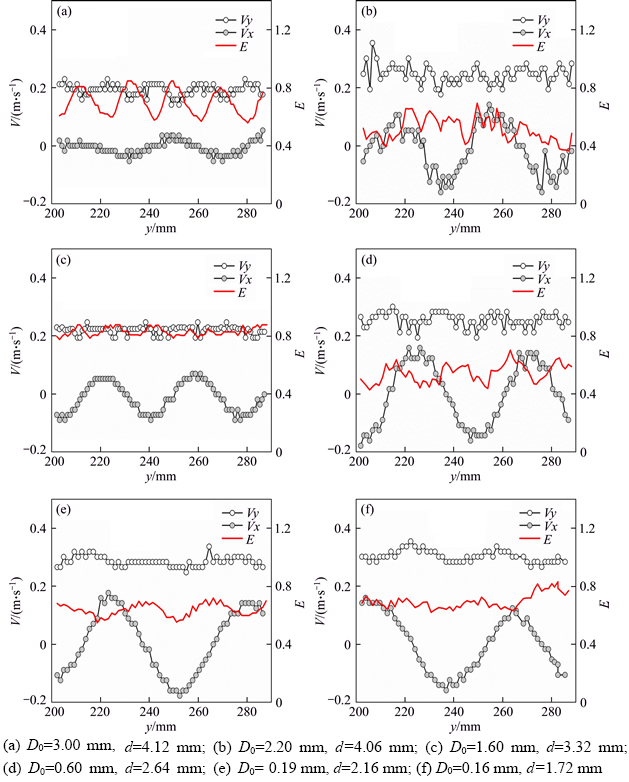

Figure 9 Variation of bubble aspect ratio and velocity components as bubble rises in Region B:

Figure 10 Comparison of bubble geometry at different air flow rates with nozzle of D₀=2.20 mm:

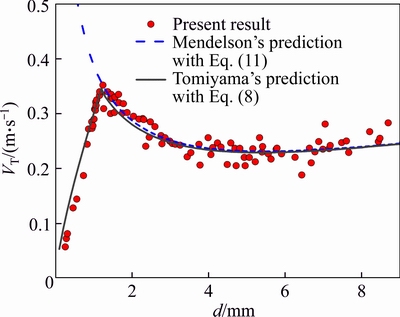
Figure 11 Variation of bubble terminal velocity with equivalent bubble diameter in Region B

At 1.2 mm≤d<3.5 mm, V_T decreases gradually as d increases, and data points of V_T are well situated near the two empirical curves. For 3.5 mm≤ d<8.69 mm, it is seen that the data points are sparsely distributed and the deviation between the data points obtained in the present study and the two empirical relations is apparent. In this context, the effects of the bubble surface deformation play an important role. From an overall view, the data of large bubbles can still be fitted with the empirical relations. Therefore, within the whole range of bubble size considered here, the effect of nozzle outlet diameter is negligible as the rising bubble reaches the state of equilibrium. Furthermore, although the bubble geometry is intricate for large bubbles, the tendency of the variation of the bubble terminal velocity with the equivalent bubble diameter is statistically stable.

4 Conclusions

1) Evolution of the rising bubble depends significantly on bubble size. Large bubble is featured by evident transitions from ellipsoidal shape, hat shape, mushroom shape and finally to ellipsoidal shape. Small bubble attains spherical shape rapidly after it detaches from the nozzle. The oscillation of the bubble surface is reinforced as bubble size increases.

2) Consecutive stages with various patterns of bubble velocity fluctuations and bubble trajectories are experienced, irrespective of bubble size. Large bubble is associated with slight variation in the horizontal bubble velocity. Sinusoidal trajectories are common for all bubble sizes but large bubble is associated with relatively straight trajectory.

3) The existing empirical relations are extended with large bubble diameters considered in the present work. The deviation between the present data and the empirical relations is evident for large bubbles, as is ascribed to reinforced surface oscillation. Nevertheless, the data of large bubbles can be roughly fitted with the empirical relations.

Acknowledgements

The authors also appreciate the suggestions from the technicians of Cinv Optical Instruments Co., LTD in evaluating the uncertainty of the bubble visualization experiment.

References

[1] SRINOI P, SATO K. Controllable air-bubbles size generator performance with swirl flow [J]. Engineering, Technology & Applied Science Research, 2015, 8(4): 245–249.

[2] ONOE K, WADA Y, MATSUMOTO M. Fascination and engineering application of reaction field utilizing fine bubbles [J]. Japanese Journal of Multiphase Flow, 2016, 30(1): 27–36.

[3] NAGAMI Y, SAITO T. An experimental study of the modulation of the bubble motion by gas–liquid-phase interaction in oscillating-grid decaying turbulence [J]. Flow, Turbulence and Combustion, 2014, 92(1): 147–174.

[4] SINGH K K, GEBAUER F, BART H J. Bouncing of a bubble at a liquid-liquid interface [J]. AIChE Journal, 2017, 63(7): 3150–3157.

[5] SCHWARZ S, FRHLICH J. Numerical study of single bubble motion in liquid metal exposed to a longitudinal magnetic field [J]. International Journal of Multiphase Flow, 2014, 62(2): 134–151.

[6] LI Shao-bai, YAN Zheng, LI Run-dong, WANG Lei, LUAN Jing-de. Numerical simulation of single bubble rising in shear-thinning fluids by level set method [J]. Journal of Central South University, 2016, 23: 1000–1006.

[7] BHM L, BREHMER M, KRAUMEM. Comparison of the single bubbleascent in a Newtonian and a non-Newtonian liquid: A phenomenological PIV study [J]. Chemie Ingenieur Technik, 2015, 88: 1–2.

[8] YOSHIDA K, MORIOKA S, KAGAWA Y. Power-law dependence describing subharmonic generation from a non-spherically oscillating bubble [J]. Acoustical Science and Technology, 2015, 36(3): 191–200.

[9] LIU L, YAN H, ZHAO G, ZHANG J. Experimental studies on the terminal velocity of air bubbles in water and glycerol aqueous solution [J]. Experimental Thermal and Fluid Science, 2016, 78: 254–265.

[10] OKAMOTO R, ONUKI A. Bubble formation in water with addition of a hydrophobic solute [J]. The European Physical Journal E, 2015, 38: 72. DOI: https://doi.org/10.1140/epje/ i2015- 15072-9.

[11] ZAWALA J, WIERTEL A, NIECIKOWSKA A, MALYSA K. Influence of external vibrations on bubble coalescence time at water and oil surfaces—Experiments and modelling [J]. Colloids and Surfaces A, 2017, 519: 137–145.

[12] ORTIZ-VILLAFUERTE J, SCHEMIDL W D, HASSAN Y A. Three-dimensional PIV measurements of bubble drag and lift coefficients in restricted media [J]. Revista Mexicana de Física, 2013, 59: 444–452.

[13] QUINN J J, MALDONADO M, GOMEZ C O, FINCH J A. Experimental study on the shape–velocity relationship of an ellipsoidal bubble in inorganic salt solutions [J]. Minerals Engineering, 2014, 55(1): 5–10.

[14] XIN Z, DONG H, DI B, KOIDE T. Effect of small amount of water on CO₂ bubble behavior in ionic liquid systems [J]. Industrial and Engineering Chemistry Research, 2014, 53(1): 428–439.

[15] LAQUA K, MALONE K, HOFFMANN M, KRAUSE D, SCHLUTER M. Methane bubble rise velocities under deep-sea conditions-influence of initial shape deformation [J]. Colloids and Surfaces A, 2016, 505: 106–117.

[16] CELATA G P, CUMO M, D’ANNIBALE F, MARCO P D, TOMIYAMA A, ZOVINI C. Effect of gas injection mode and purity of liquid on bubble rising in two-component systems [J]. Experimental Thermal and Fluid Science, 2006, 31(1): 37–53.

[17] KANG Can, ZHANG Wei, GU Yi-ping, MA Ning. Bubble size and flow characteristics of bubbly flow downstream of a ventilated cylinder [J]. Chemical Engineering Research and Design, 2017, 122: 263–272.

[18] ZHANG Wei, NESSET J E, FINCH J A. A novel approach to prevent bubble coalescence during measurement of bubble size in flotation [J]. Journal of Central South University, 2014, 21: 338–343.

[19] DEHAECK S, PARYS H V, HUBIN A, BEECK J P A J V. Laser marked shadowgraphy: A novel optical planar technique for the study of microbubbles and droplets [J]. Experiments in Fluids, 2009, 47: 333–341.

[20] ZHANG A M, CUI P, CUI J, WANG Q. Experimental study on bubble dynamics subject to buoyancy [J]. Journal of Fluid Mechanics, 2015, 776: 137–160.

[21] TOMIYAMA A, KATAOKA I, ZUN I, SAKAGUCHI T. Drag coefficients of single bubbles under normal and micro gravity conditions [J]. JSME International Journal Series B, 1998, 41(2): 472–479.

[22] MENDELSON H D. The prediction of bubble terminal velocities from wave theory [J]. AIChE Journal, 2010, 13(2): 250–253.

(Edited by YANG Hua)

中文导读

初始尺寸对气泡在水中的几何和运动特征的影响

摘要：为了探究和描述气泡尺寸对气泡的几何形态及运动学特征的影响，使用6种不同直径的喷嘴采用向水中通气的方法产生了不同尺寸的气泡，采用高速摄像系统对气泡图像进行采集，并结合专门开发的软件分析了气泡发展过程中的形状、运动轨迹和速度的变化。实验过程中获得的气泡尺寸范围为0.25~8.69 mm。结果表明，气泡脱离喷嘴后，气泡形态依次经由椭球形、球帽形、蘑菇形，最终转变为稳定的椭球形。随着气泡尺寸的增大，气泡表面的波动加剧。在气泡运动的稳定阶段，气泡的轨迹可近似用正弦曲线来描述。同时，随着气泡尺寸的增大，气泡轨迹有被拉直的趋势，横向分速度对气泡轨迹的影响减弱。研究结果解释了与大尺寸气泡相关的现象，拓展了已发表的气泡终速度与气泡当量直径之间的关系。

关键词：气泡尺寸；喷嘴直径；气泡变形；纵横比；气泡终速度

Foundation item: Project(51676087) supported by the National Natural Science Foundation of China

Received date: 2017-10-17; Accepted date: 2018-06-25

Corresponding author: KANG Can, PhD, Professor; Tel: +86-511-88780217; E-mail: kangcan@mail.ujs.edu.cn; ORCID: 0000-0002- 1152-0787