拼焊板成形性能的理论预测与实验研究
来源期刊:中国有色金属学报(英文版)2016年第1期
论文作者:马向东 官英平
文章页码:228 - 236
关键词:拼焊板;成形极限图;纳米压痕实验;半球凸模胀形实验
Key words:tailor-welded blank; forming limit diagram; nanoindentation test; hemispherical punch bulging test
摘 要:基于塑性本构关系和Hosfrod屈服准则,当拼焊板焊缝及热影响区金属的弹塑性力学性能已知时,提出一种获得拼焊板成形极限图的理论计算方法。建立获取拼焊板成形极限图的半球凸模胀形物理实验模型,并将物理实验结果与理论计算结果进行对比分析。研究结果表明:拼焊板及其母材成形极限图的理论计算结果与物理实验结果吻合较好;拼焊板的成形极限明显低于母材,说明拼焊板与母材相比,成形性能降低。该理论计算模型为快速准确获得拼焊板的成形极限图提供了一种方法。
Abstract: Based on the elastoplastic mechanical properties of the weld and heat affected zone metals obtained by a nanoindentation test, a theoretical calculation model was established for the forming limit diagram (FLD) of tailor-welded blanks (TWBs) on the basis of plastic constitutive relations and Hosford yield criteria. Hemispherical punch bulging tests were performed to verify the FLD theoretical calculation results. The results demonstrated that not only the FLD theoretical calculation of base materials but also that of TWBs had a good agreement with their experiments. Besides, poorer formability of TWBs caused its FLD significantly lower than that of base materials. The theoretical calculation model offers a reliable approach to obtain the specific FLD of TWBs.
Xiang-dong MA, Ying-ping GUAN
Key Laboratory of Advanced Forming and Stamping Technology and Science of
Ministry of Education of China, Yanshan University, Qinhuangdao 066004, China
Received 12 February 2015; accepted 14 September 2015
Abstract: Based on the elastoplastic mechanical properties of the weld and heat affected zone metals obtained by a nanoindentation test, a theoretical calculation model was established for the forming limit diagram (FLD) of tailor-welded blanks (TWBs) on the basis of plastic constitutive relations and Hosford yield criteria. Hemispherical punch bulging tests were performed to verify the FLD theoretical calculation results. The results demonstrated that not only the FLD theoretical calculation of base materials but also that of TWBs had a good agreement with their experiments. Besides, poorer formability of TWBs caused its FLD significantly lower than that of base materials. The theoretical calculation model offers a reliable approach to obtain the specific FLD of TWBs.
Key words: tailor-welded blank; forming limit diagram; nanoindentation test; hemispherical punch bulging test
1 Introduction
Tailor-welded blanks (TWBs) are constituted of two or more materials with different strengths or thicknesses or surface coatings joined together to form a single part before the forming process [1]. TWBs play a great important role in reducing the mass and enhancing the safety of automotive body structures [2]. In recent years, with the increasingly high society demand of environment protection and energy conservation, applications of TWBs are wider and wider in the automotive industry. However, due to the different thicknesses or different strengths of TWBs base materials and the presence of weld nugget (WN) and heat affected zone (HAZ), the forming technology for TWBs is very different with that for conventional single sheet. Many new technical issues of TWBs forming have not been well solved, such as the reduced forming limit, weld line movement and other problems [3,4].
The concept of FLD was first developed by KEELER and BACKOFEN [5] with experimental testing for tension-tension deformations and GOODWIN [6] for tension-compression deformations, mostly represented as the in-plane major principal strain (ε1) versus the in-plane minor principal strain (ε2) that a sheet metal can undergo before the occurrence of necking or cracking in all possible tension and compression strain paths during the forming process. Many experimental and numerical approaches were proposed to obtain the FLD of sheet metals. JAHROMI et al [7] determined experimentally for the FLD of three grades steels, and then discussed the strain hardening exponent (n), plane anisotropy (r) and sheet orientation on the influence of FLD. LIU and XUE [8] studied experimentally on the formability of three kinds of AA5052/polyethylene/AA5052 sandwich sheets with different thicknesses of core materials. LEE et al [9] used hemispherical dome stretching test to assess the formability of five friction stir welding automotive sheets, and noticed that the formability of TWB sheets in forming process mainly depended on the weld zone line arrangement as well as the weld zone ductility and strength. GAIED et al [10] presented a numerical simulation model to predict the forming limit curve of TWBs, and found that the numerical simulation and experimental results are very consistent. All of the above formability researches used either numerical simulation or hemispherical punch bulging tests, but both of them needed a longer time or higher cost. BANDYOPADHYAY et al [11] developed a mathematical framework to estimate stress-based forming limit diagram of TWBs from strain-based forming limit diagram using Hill-48 and Barlat-89 anisotropic plasticity theories, and observed that the stress-based forming limit diagram was more robust compared with the strain-based forming limit diagram, especially under complex strain state forming. However, stress-based forming limit diagram can only be obtained by the experimental limit strain and plastic yield criterion indirectly, and the results are greatly related to the measurement accuracy of limit strain. MOHEBBI and AKBARZADEH [12] calculated the FLD of TWBs relied on the modification of M-K theoretical method and imposed the weld constraints to deformation state of each blank at each strain increment. However, this method required material constants and the levels of initial material imperfection.
In view of the above shortcomings, the main objective of the present work is to establish the FLD theoretical calculation models for TWBs and their base materials based on the plastic constitutive relations and Hosford yield criteria. The elastoplastic mechanical properties of the TWBs weld and heat affected zone metals are obtained by a nanoindentation test. The hemispherical punch bulging tests are performed for the FLD of TWBs and their base materials, and then the experimental results of FLD are compared with their theoretical calculation results.
2 Theoretical models of FLD
2.1 FLD model for TWBs base materials
The stress state of plate deformation can be approximated as plane stress state, that is, the principal stress in thickness direction (σ3) is 0. The following equation can be obtained according to the Hill anisotropic plasticity theory [13]:
 (1)
(1)
where 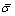 and
and  represent the effective stress and effective strain increment, respectively.
represent the effective stress and effective strain increment, respectively. 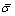 and
and  are expressed as follows:
are expressed as follows:
 (2)
(2)
 (3)
(3)
where σ1 and σ2 are the major and minor principal stresses, respectively; dε1 and dε2 are the major and minor principal strains increment, respectively; R is the anisotropy coefficient.
Under the simple loading condition, it is assumed that the principal stress ratio α=σ2/σ1, the principal strain ratio β=ε2/ε1, the effective stress and the relationship between effective strain and principal strain are expressed as follows:
 (4)
(4)


 (5)
(5)
In tension-tension strain area, that is the right side of forming limit diagram, the expressions of major and minor strains can be obtained on the basis of Swift instability criterion, namely,
 (6)
(6)
In tension-compression strain area, that is the left side of forming limit diagram, the expressions of major and minor strains can be obtained on the basis of the Hill instability criterion, namely,
 (7)
(7)
At this point, the FLD of TWBs base materials can be gained by Eqs. (6) and (7). In above equations, n is strain hardening exponent; ε1f and ε2f represent the limit major and minor strain respectively in tension-tension strain area; εj1 and εj2 represent the limit major and minor strain respectively in tension-compression strain area.
2.2 FLD model for TWBs
TWBs are composed of base materials A, B, and welded zone (WN and HAZ) W, as shown in Fig. 1. Due to the small molten pool, large temperature gradient and thermal conduction in the process of TWB welding, the martensite easily appeared in the weld and heat affected zone, resulting in metals with high hardness, poor plasticity in the TWB weld and heat affected zone and abnormal mechanical behavior during deformation [14]. Consequently, the theoretical model of TWB forming limit diagram should reflect the restriction effect of weld metals on base materials. Theoretical analysis model for the TWB forming limit diagram is shown in Fig. 2. F, σ and ε represent the force, stress and strain, respectively. Subscripts 1 and 2 indicate major and minor strain (or stress) direction, respectively. Subscripts A and W indicate force (or strain or stress) on the base material A and welded zone metals W, respectively. The weld and heat affected zones act as a force transmission during the TWBs deformation because of its high hardness and low deformation ability.

Fig. 1 Schematic diagram of TWBs

Fig. 2 Theoretical analysis model of TWB forming limit diagram
According to the force equilibrium condition, the force of 1-direction can be given by
F1A=F1W (8)
It is assumed that the strain increment of base material and weld metals are equal in 2-direction during the whole deforming process, namely,
dε2A= dε2W (9)
Equation (8) can be further converted as
 (10)
(10)
where ε3A and ε3W are the thick strains of base material A and welded zone metals W, respectively; tA0 and tW0 are the initial thicknesses of base material A and welded zone metals W, respectively.
The Swift law was used as strain hardening behavior [15], which was expressed as follows:
 (11)
(11)
where 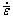 is the effective strain rate; m is the strain sensitivity coefficient; K is the strength coefficient; n is the strain hardening exponent.
is the effective strain rate; m is the strain sensitivity coefficient; K is the strength coefficient; n is the strain hardening exponent.
φ is defined as effective stress divided by the first principal stress:
 (12)
(12)
Combining Eqs. (11) and (12), Eq. (10) can be changed as

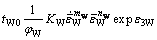 (13)
(13)
ρ is defined as minor strain increment divided by major strain increment, γ is the effective strain increment divided by major strain increment, and they are described as follows:
 ,
,  (14)
(14)
It is assumed that the strain sensitivity coefficients of base material and welded zone metals are equal, that is mA=mW=m. When effective strain  increases with
increases with  , Eq. (13) can be transformed as
, Eq. (13) can be transformed as

 (15)
(15)
In this work, plastic behavior of the plates is formulated by the Hosford yield criterion [16], which is described as follows:
 (16)
(16)
where μ is the stress exponent; R is the anisotropy coefficient.
By combining Eqs. (12) with (16), Eq. (16) can be converted as
 (17)
(17)
Based on the plastic flow rule, the Eq. (17) can be expressed as
 (18)
(18)
According to the above analysis, theoretical calculation of the TWB forming limit diagram has been converted into solving the nonlinear Eq. (15). From Eq. (15), we can see that under a certain strain ratio, the limit strains of TWBs can be easily obtained when the elastoplastic mechanical properties of weld and heat affected zone metals (KW and nW) are determined.
Nonlinear Eq. (15) is solved by the Newton- Raphson iteration method, and its algorithmic flowchart is illustrated in Fig. 3. Firstly, the mechanical properties of TWBs base materials (KA and nA) and its weld and heat affected zone metals (KW and nW) were determined, which will be described in Section 3. Secondly, a strain increment of Δε1W in weld and heat affected zone area was applied which is perpendicular to the weld line (1-direction) under a certain strain ratio, and then the strain increment of Δε1A in base material area was calculated according to the mechanical equilibrium
Eq. (15). Thirdly, the failure criterion f was set, if Δε1A/Δε1W was less than or equal to the f, considering that the TWB does not reach the limit strain, and then a strain increment of Δε1E was supposed once again in weld and heat affected zone area in foundation of above deformation, a new strain increment of Δε1A was calculated. Finally, the above steps were repeated until Δε1A/Δε1W was greater than failure criterion f, and the iteration ends. The main strain ε1W and minor strain ε2W at this moment are the limit strains of TWBs in strain ratio, and changing the strain ratio can obtain the FLD of TWBs completely.
3 Mechanical properties of TWB base materials and welded zone metals
Cold rolling ST12 steel plates with thicknesses of 0.8 mm and 1.2 mm were used in this work. The chemical composition of base materials is shown in Table 1. The elastoplastic mechanical properties of base materials were obtained by a uniaxial tensile test on Inspekt 100 kN universal electronic material testing machine. Along rolling direction, 45 degrees to the rolling direction and perpendicular to the rolling direction, three kinds of uniaxial tensile specimens were cut by wire cutting machine, of which the dimensions followed the guidelines of ASTM E8 [17]. The elastoplastic mechanical properties of base materials are shown in Table 2.

Fig. 3 Algorithmic flowchart of TWB FLD
Table 1 Chemical composition of base material St12 (mass fraction, %)

Table 2 Elastoplastic mechanical properties of base material ST12

Two types of TWBs were studied in this work: TWBs of the same materials with same thicknesses, ST12 (0.8 mm)/ST12 (0.8 mm), and TWBs of the same materials with different thicknesses, ST12 (0.8 mm)/ ST12 (1.2 mm). In order to facilitate the expression, these two aforementioned types of TWBs are defined as TWB1 and TWB2, respectively. All of the welding experiments were carried out with a pulse laser welding machine (Model: HC-AW300), as shown in Fig. 4. The welding current, laser frequency, pulse width and welding speed are 150 A, 20 Hz, 4.5 ms and 120 mm/min, respectively. Additionally, the welding direction is parallel to the rolling direction of base materials.

Fig. 4 Apparatus of TWB laser welding processing
The elastoplastic mechanical properties of the weld and heat affected zone metals were obtained by a nanoindentation test, which is a more advanced testing method without damage or micro damage for mechanical properties of micro samples or the local area of normal samples [18]. Theoretical bases of nanoindentation tests were introduced particularly in Refs. [19-22]. All of the nanoindentation tests were carried out with a TRIBOINDENTER nanoindentation instrument which was produced by HYSITRON company, as shown in Fig. 5(a). The Berkovich indenter was used with an interior angle of 130.6°, as shown in Fig. 5(b). 20 test points were linearly arranged with equal interval on the specimens of base materials, weld nugget and heat affected zone metals, as shown in Fig. 5(c). A load of 5000 μN was applied on each test point, and the strain rate was set to be 0.05 s-1 during the entire process of loading and unloading. In order to make the initial slope of unloading curve clear, the pressure was held for 10 s when the loading reached the maximum, then unloaded completely. The measured loading and unloading curves of load-indentation depth (P-h) relation for one point are schematically shown in Fig. 5(d), from which the mechanical parameters K and n can be accurately determined. The analysis procedures refer to Ref. [23].

Fig. 5 TRIBOINDENTER nanoindentation instrument (a), microscopic view of appearance on sample (b), distribution of test points (c) and typical P-h curve for one test point (d)
Figure 6 shows the mechanical properties with strength coefficient K and strain hardening exponent n of TWB1 and TWB2 distributed in cross section. From Fig. 6, it can be seen that the strength coefficient commonly increases with decreasing distance from the welded centerline. The strain hardening exponent, however, exhibits an opposite variation tendency to that of strength coefficient. In addition, both ST12 base materials with different thicknesses were produced from Anshan Iron and Steel Group Corporation, and their true stress-true strain curves of the gap were very small and the maximum difference between their true stresses was 13.87 MPa. Therefore, the mechanical properties of the TWB1 and TWB2 weld and heat affected zone metals are very similar. In order to take mechanical properties K and n of the weld and heat affected zone metals into theoretical model of the TWB FLD (described in Section 2.2), the entire weld and heat affected zones are assumed to be homogeneous and their properties were obtained by averaging the data of the test points located in this zone.

Fig. 6 Elastoplastic mechanical properties of TWB1 and TWB2 weld and heat affected zones metals: (a) Strength; (b) Strain hardening exponent
4 Experimental processes for FLD
For experimental determination of the tailor-welded blank and base materials FLD, hemispherical punch bulging tests were carried out according to the international standard ISO 120004-2 [24] on a BCS-50A sheet metals forming performance test machine, as shown in Fig. 7(a), and the schematic diagram of mould structure is shown in Fig. 7(b). In the experiment, hemispherical punch diameter was 100 mm, punch speed was 35 mm/min, and the applied blank holder force was 110 kN. Polyethylene film wrapped Vaseline was utilized as lubricants between the moulds and blank. Patterns of square grid with a size of 2 mm were marked on the blank surfaces by electric corrosion marking machine (as shown in Fig. 7(c)) to measure the major and the minor strains induced in the specimen after deformation. The major and minor principal strains in the vicinity of crack were conducted by the AutoGrid Comsmart strain measurement system, as shown in Fig. 7(d). All the experiments were stopped when an obvious neck or initiation of fracture occurred on the specimens. The test sheet metal samples had the same length of 180 mm but different widths, varying from 20 to 180 mm, in order to obtain the limit strain in different strain states. Geometric sizes of the test samples are shown in Fig. 8.
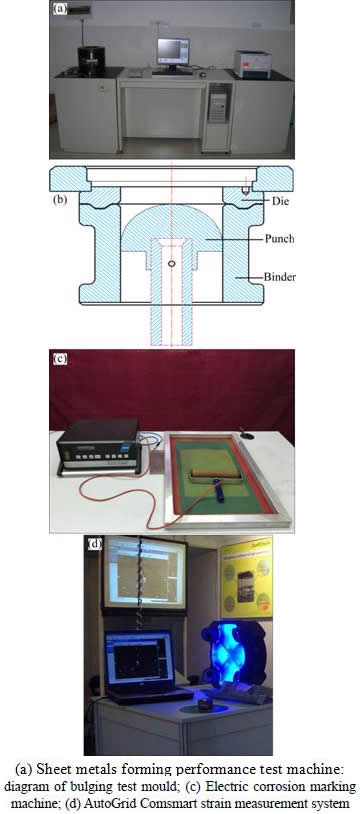
Fig. 7 Hemispherical punch bulging test set-up

Fig. 8 Geometric sizes of test samples (unit: mm)
5 Results and discussion
From experimental hemispherical punch bulging tests with the AutoGrid Comsmart strain measurement system and theoretical calculation, the FLDs of investigated base materials of TWBs, ST12 with thicknesses of 0.8 mm and 1.2 mm, were determined and shown in Fig. 9. The theoretical calculation results of forming limit curves for TWBs base materials have a good agreement with experimental results, and the forming limit curve of the ST12 with thickness of 1.2 mm is slightly higher than that with thickness of 0.8 mm in both tension-tension and tension- compression strain areas. The main reason behind this phenomenon is the higher strain hardening exponent n of ST12 with thickness of 1.2 mm than that with thickness of 0.8 mm, which are listed in Table 2. Additionally, the formed samples of hemispherical punch bulging tests are shown in Fig. 10. It can be observed that the test samples crack or neck at the top of hemispherical punch area in uniaxial tension stress state, but in biaxial tension stress state near the top of hemispherical punch area.
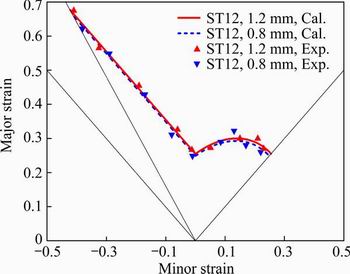
Fig. 9 Theoretical and experimental results of TWB base materials FLD

Fig. 10 Formed samples after failure in hemispherical punch bulging tests
In theoretical calculation process of FLD for tailor-welded blanks, the strain sensitivity coefficient m was 0.015, the stress exponent μ was 6, the thickness anisotropy coefficient of weld area RW was 1.06, and the failure criterion f was set to be 10. Visual Basic was used to calculate the FLD of tailor-welded blanks, and the algorithmic flowchart is presented in Fig. 3. The comparison diagram of tailor-welded blanks forming limit curves based on the theoretical calculation and physical experiment is shown in Fig. 11. The theoretical calculation results of forming limit curves for TWBs are well consistent with those of experiments, but significantly less than the forming limit curves of base materials. This can be related to the high strength of weld and heat affected zone areas relative to base materials. In the initial stage of deformation, the load increases steadily and the strain path keeps linearly. High strength of weld and heat affected zone regions cannot deform freely as the deformation continues, which restricts the plastic flow of base material adjacent to weld and heat affected zone regions in weld line direction and affects the strain path drifting. Therefore, the strain state of base materials gradually becomes plane strain state, that is dε2A=0, localized necking occurs, and the TWBs achieve limit strain state.

Fig. 11 Comparison between experimental and theoretical FLDs for investigated TWBs
6 Conclusions
1) The FLDs of two types of TWBs (TWB1 and TWB2) and their base materials were investigated by the theoretical analysis method. Swift instability criterion and Hill instability criterion were used for the FLD of base materials in both tension-tension strain and tension-compression strain areas. The mechanical equilibrium equation and Hosford yield criterion were used to calculate the FLD of TWBs when the elastoplastic mechanical properties of the TWBs weld and heat affected zone metals are known.
2) The elastoplastic mechanical properties of the TWBs weld and heat affected zone metals are obtained by a nanoindentation test. The strength coefficient commonly increases with decreasing distance from the welded center line. The strain hardening exponent, however, presents an opposite variation tendency.
3) Hemispherical punch bulging tests were carried out to determine the FLD of TWBs and their base materials. Not only the theoretical calculation result of TWBs, but also that of their base materials has a good agreement with experimental result. The forming limit curve of the ST12 with thickness of 1.2 mm is slightly higher than that with thickness of 0.8 mm, but significantly more than the forming limit curves of TWB1 and TWB2.
References
[1] MERKLEIN M, JOHANNES M, LECHNER M, KUPPERT A. A review on tailored blanks-Production, applications and evaluation [J]. Journal of Materials Processing Technology, 2014, 214(2): 151-164.
[2] ABBASI M, KETABCHI M, RAMAZANI A, ABBASI M, PRAHL U. Investigation into the effects of weld zone and geometric discontinuity on the formability reduction of tailor welded blanks [J]. Computational Materials Science, 2012, 59: 158-164.
[3] VEERA B K, GANESH N R, SARAVANA K G. An expert system for predicting the deep drawing behavior of tailor welded blanks [J]. Expert Systems with Applications, 2010, 37(12): 7802-7812.
[4] KOKLU U. Investigation into the formability of Al-1050 tailor-welded blanks with antilock braking system [J]. International Journal of Advanced Manufacturing Technology, 2013, 66(1-4): 221-229.
[5] KEELER S P, BACKOFEN W A. Plastic instability and fracture in sheets stretched over rigid punches [J]. ASM Transactions Quarterly, 1963, 56(11): 25-48.
[6] GOODWIN G M. Application of strain analysis to sheet metal forming problems in the press shop [J]. SAE Transactions, 1968, 77: 380-387.
[7] JAHROMI S A, NAZARBOLAND A, MANSOURI E, ABBASI S. Investigation of formability of low carbon steel sheets by forming limit diagrams [J]. Iranian Journal of Science & Technology B, 2006, 30(3): 377-385.
[8] LIU Jian-guang, XUE Wei. Formability of AA5052/polyethylene/ AA5052 sandwich sheets [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(4): 964-969.
[9] LEE W, CHUNG K H, KIM D, KIM J, KIM C, OKAMOTO K, WAGONER R H, CHUNG K. Experimental and numerical study on formability of friction stir welded TWB sheets based on hemispherical dome stretch tests [J]. International Journal of Plasticity, 2009, 25(9): 1626-1654.
[10] GAIED S, ROELANDT J M, PINARD F, SCHMIT F, BALABANE M. Experimental and numerical assessment of tailor-welded blanks formability [J]. Journal of Materials Processing Technology, 2009, 209(1): 387-395.
[11] BANDYOPADHYAY K, BASAK S, PANDA S K, SAHA P. Use of stress based forming limit diagram to predict formability in two-stage forming of tailor welded blank [J]. Materials & Design, 2015, 67: 558-570.
[12] MOHEBBI M S, AKBARZADEH A. Prediction of formability of tailor welded blanks by modification of MK model [J]. International Journal of Mechanical Sciences, 2012, 61(1): 44-51.
[13] HILL R. A theory of the yielding and plastic flow of anisotropic metals [J]. Proceedings of the Royal Society A, 1948, 193(1033): 281-297.
[14] ABDULLAH K, WILD P M, JESWIET J J, GHASEMPOOR M. Tensile testing for weld deformation properties in similar gage tailor welded blanks using the rule or mixtures [J]. Journal of Materials Processing Technology, 2001, 112(1): 91-97.
[15] SWIFT H W. Plastic instability under plane stress [J]. Journal of the Mechanics and Physics of Solids, 1952, 1(1): 1-18.
[16] GRAF A, HOSFORD W F. Calculations of forming limit diagrams [J]. Metallurgical & Materials Transactions A, 1990, 21(1): 87-94.
[17] ASTM E8/E8M. Standard test methods for tension testing of metallic material [S]. 2009.
[18] ZORZI J E, PEROTTONI C A. Estimating Young’s modulus and Poisson’s ratio by instrumented indentation test [J]. Materials Science and Engineering A, 2013, 574: 25-30.
[19] VENKATESH T A, VAN K J, GIANNAKOPOULS A E, SURESH S. Determination of elastoplastic properties by instrumented sharp indentation: guidelines for property extraction [J]. Scripta Materialia, 2000, 42(9): 833-839.
[20] GIANNAKOPOULOS A E, SURESH S. Determination of elastoplastic properties by instrumented sharp indentation [J]. Scripta Materialia, 1999, 40(10): 1191-1198.
[21] GIANNAKOPOULOS A E, LARSON L P, VESTERGAARD R. Analysis of Vickers indentation [J]. International Journal of Solids and Structures, 1994, 31(19): 2679-2708.
[22] SURESH S, GIANNAKOPOULOS A E. A new method for estimating residual stress by instrumented sharp indentation [J]. Acta Materialia, 1998, 46(16): 5755-5767.
[23] SONG Y L, HUA L MENG F Z. Inhomogeneous constructive modeling of laser welded bead based on nanoindentation test [J]. Iron Making and Steelmaking, 2012, 39(2): 95-103.
[24] ISO 12004-2. Metallic materials–sheet and strip–determination of forming limit curves, Part 2: Determination of forming limit curves in the laboratory [S]. 2008.
马向东,官英平
燕山大学 先进锻压成形技术与科学教育部重点实验室,秦皇岛 066004
摘 要:基于塑性本构关系和Hosfrod屈服准则,当拼焊板焊缝及热影响区金属的弹塑性力学性能已知时,提出一种获得拼焊板成形极限图的理论计算方法。建立获取拼焊板成形极限图的半球凸模胀形物理实验模型,并将物理实验结果与理论计算结果进行对比分析。研究结果表明:拼焊板及其母材成形极限图的理论计算结果与物理实验结果吻合较好;拼焊板的成形极限明显低于母材,说明拼焊板与母材相比,成形性能降低。该理论计算模型为快速准确获得拼焊板的成形极限图提供了一种方法。
关键词:拼焊板;成形极限图;纳米压痕实验;半球凸模胀形实验
(Edited by Xiang-qun LI)
Foundation item: Project (51275444) supported by the National Natural Science Foundation of China; Project (20121333110003) supported by the Specialized Research Fund for the Doctoral Program of Higher Education, China; Project (E2014203271) supported by the Natural Science Foundation–Steel and Iron Foundation of Hebei Province, China
Corresponding author: Ying-ping GUAN; Tel: +86-335-8074686; Email: gyp@ysu.edu.cn
DOI: 10.1016/S1003-6326(16)64108-0

