J. Cent. South Univ. (2019) 26: 824-838

DOI: https://doi.org/10.1007/s11771-019-4052-4

Impulsive component extraction using shift-invariant dictionary learning and its application to gear-box bearing early fault diagnosis

ZHANG Zhao-heng(张兆珩)¹, DING Jian-ming(丁建明)¹, WU Chao(吴超)², LIN Jian-hui(林建辉)¹

1. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China;

2. CRRC Zhuzhou Locomotive Co., Ltd, Zhuzhou 412001, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: The impulsive components induced by bearing faults are key features for assessing gear-box bearing faults. However, because of heavy background noise and the interferences of other vibrations, it is difficult to extract these impulsive components caused by faults, particularly early faults, from the measured vibration signals. To capture the high-level structure of impulsive components embedded in measured vibration signals, a dictionary learning method called shift-invariant K-means singular value decomposition (SI-K-SVD) dictionary learning is used to detect the early faults of gear-box bearings. Although SI-K-SVD is more flexible and adaptable than existing methods, the improper selection of two SI-K-SVD-related parameters, namely, the number of iterations and the pattern lengths, has an adverse influence on fault detection performance. Therefore, the sparsity of the envelope spectrum (SES) and the kurtosis of the envelope spectrum (KES) are used to select these two key parameters, respectively. SI-K-SVD with the two selected optimal parameter values, referred to as optimal parameter SI-K-SVD (OP-SI-K-SVD), is proposed to detect gear-box bearing faults. The proposed method is verified by both simulations and an experiment. Compared to the state-of-the-art methods, namely, empirical model decomposition, wavelet transform and K-SVD, OP-SI-K-SVD has better performance in diagnosing the early faults of a gear-box bearing.

Key words: gear-box bearing; fault diagnosis; shift-invariant K-means singular value decomposition; impulsive component extraction

Cite this article as: ZHANG Zhao-heng, DING Jian-ming, WU Chao, LIN Jian-hui. Impulsive component extraction using shift-invariant dictionary learning and its application to gear-box bearing early fault diagnosis [J]. Journal of Central South University, 2019, 26(4): 824–838. DOI: https://doi.org/10.1007/s11771-019-4052-4.

1 Introduction

A gear-box bearing, as a key component of a gear-box system, plays an important role in maintaining the stable transmission of the gear. However, faults in a gear-box bearing can occur easily because of the comprehensive effects of long-term alternating transmission loads, unsuitable cooperation and manufacture error, and these unfavorable factors finally endanger the safety of high-speed train service [1, 2]. Therefore, the running condition of a gear-box bearing must be monitored.

Acceleration-based vibration monitoring is a feasible method for running condition monitoring that is widely applied in industrial applications because of its effectiveness, lower cost and convenient installation [3, 4]. When there is a defect on the surface of gear-box bearing components, a series of impulsive components will be generated with the rotation of the gear axle [5]. However, the excited impulsive components are typically fairly weak and can be easily masked by other types of interference, such as gear mesh and structure vibration. Therefore, extraction of those impulsive components from the measured vibration signals remains difficult [6].

Many advanced signal processing methods have been proposed to overcome difficulties mentioned above, such as time-domain analysis, frequency-domain analysis and time-frequency analysis. In time-domain analysis, statistical indicators, such as the mean, root mean square and kurtosis factor, are used to analyze the vibration signals to monitor the running condition of the gear- box [7]. Frequency-domain analysis, also known as spectrum analysis, can provide information regarding the status of gear-box in the format of spectrum lines, and the frequency components of interest can be easily identified in the frequency domain [8]. However, time-domain statistic indicators simultaneously contain the time-varying operation condition of the gear-box and its running information, which may cause it to be invalid under certain conditions. Frequency-domain analysis is intrinsically not suitable for analyzing such non-stationary signals induced by gear-box bearing faults [9]. Time-frequency analysis, as a kind of methods for processing a non-stationary signal, has been applied in the field of bearing fault diagnosis. Empirical mode decomposition (EMD) [10–12], short-time Fourier transformation (STFT) [13] and the Wigner-Ville distribution (WVD) [14] are the mainstream time-frequency methods in the domain of bearing fault diagnosis. However, these methods show poor indicative ability under the condition of a weak fault and heavy background noise. Wavelet transformation (WT) [15] and its extensions [16, 17] are advanced time-frequency analysis methods that have been successfully applied in the field of fault diagnosis of bearings [16] and gears [18] using a series of basic functions with different frequencies at different times to represent the given signal. Nevertheless, when the aforementioned WTs are applied to bearing fault diagnosis, a considerable amount of redundant information has been persevered [19]. The recently developed dictionary learning method provides the potential to seek the sparsest representation of the impulsive components with shift-invariant features caused by bearing faults.

Dictionary learning can directly learn a dictionary formed from a set of training signals. The learned dictionary represents the essential constituent components embedded in the analyzed signals. In this sense, the learned dictionary can reveal the high-level structure and intrinsic behaviour of the impulsive components embedded in measured signals [20]. Moreover, without any analytical expression, the learned dictionary provides more flexibility to extract the latent impulsive components in a more sparse and effective manner. Dictionary learning mainly includes regular dictionary learning and shift-invariant dictionary learning [21]. Regular dictionary learning methods include online dictionary learning (OLD) [22], the method of optimal directions (MOD) [23], K-means singular value decomposition (K-SVD) [24, 25], and the iterative least square dictionary learning algorithm (ILS-DLA) [26]. However, when the aforementioned regular dictionary learning methods are used to address the shift-invariant issues, a long signal must be split into several small segments; such segment-based dictionary learning results in multiple values and a suboptimal representation with respect to the entire signal [27]. Several shift-invariant dictionary learning methods have been proposed to address the shift-invariant issues, such as convolution sparse representation (CSR) [27], shift-invariant K-SVD algorithm (SI-K-SVD) [28], shift-invariant sparse coding (SISC) [29] and support vector machine shift-invariant dictionary learning (SVM-SIDL) [30]. These algorithms are helpful for extracting the latent similar components from a long signal. SI-K-SVD is an extension of the standard K-SVD and inherits the advantages of K-SVD of flexibility, simplicity and efficiency [31]. Moreover, SI-K-SVD eliminates the time-localized or position-sensitive problem and has a potential to solve the shift-invariant issue and obtain an optimized sparse representation of the given signal [32–34].

Although SI-K-SVD algorithm has the potential to extract these impulsive components caused by faults, its two key parameters, namely, the number of iterations and the pattern lengths, have great influences on the fault diagnosis performance. Therefore, the key step when using SI-K-SVD is to select the two parameters properly. As such, two indicators, namely, the sparsity of the envelope spectrum (SES) and the kurtosis of the envelope spectrum (KES), are employed to adaptively tune the number of iterations and the pattern lengths, respectively. SI-K-SVD with the optimal values of these two parameters, referred to as optimal parameter SI-K-SVD (OP-SI-K-SVD), is used to detect the faults of a gear-box bearing.

The remainder of this paper is organized as follows. Section 2 introduces the basic theory of SI-K-SVD and discusses the influence of SI-K- SVD-related parameters on the fault detection performance. In Section 3, the two indicators for parameter selection are discussed. Next, the simulated signals are employed to verify the proposed method in Section 4. In Section 5, experimental data of a bench test is used to validate the effectiveness of the proposed OP-SI-K-SVD. Finally, the conclusions of this paper are presented in Section 6.

2 Basic theory of SI-K-SVD and a discussion of its related parameters

2.1 SI-K-SVD

SI-K-SVD, originated from K-SVD, is a dictionary learning method that has been used to solve the shift-invariant issue. In SI-K-SVD, the target signal remains as one long signal instead of separating it into many segments, as in regular dictionary learning (e.g., K-SVD). The dictionary D containing K atoms is built by shifting a family M of normalized patterns 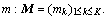Therefore, those components with similar characteristics at different locations can be represented by only one basic function in the analyzed signal. Therefore, such dictionary learning is transformed to learn a set of patterns, defined as follows [28]:

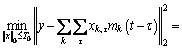
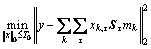                (1)

where T₀ is the nonzero entries of the sparse coefficients, ||·||₀ is the zero norm, 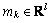represents the learned pattern, l is the pattern length, is the shift operator that takes the pattern m_k and returns an atom that is null everywhere except for a copy of m_k that starts at instant τ, and x_k,τ is the coefficient associated with the pattern m_k shifted to instant τ. Videlicet, the dictionary is defined as D=(S_τm_k)_k,τ. Specifically, the shift operator S_τ is a matrix with only l nonzero entries which equal 1 in the semi-diagonal that starts in the τth row:

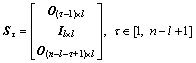            (2)

where O_k×l is a zero matrix with k rows and l columns and I_l×l means an identity matrix having l entries.

In Eq. (1), each of the patterns and its corresponding coefficients cannot be solved simultaneously because of their coupled relationship. To solve the coupling problem, before updating the next pattern, each pattern m_k and its corresponding coefficient x_k,τ are updated successively. The pattern m_k can be solved by the optimization problem below:

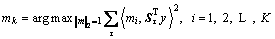  (3)

where 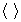is the inner product, ||·||₂ is the 2 norm and 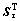denotes the transpose of S_τ. When the pattern m_k has been obtained, the corresponding coefficient x_k,τ can be solved using the following equation:

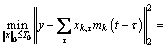
                  (4)

Unfortunately, the atoms in this dictionary are highly coherent because of the few differences between the close shifts of the pattern. Moreover, when the given signal is long, the size of dictionary will be extremely large. MP algorithm, as an efficient and economic method, performs well in solving the coherent problems [35]. Hence, MP algorithm is chosen to obtain the coefficient x_k,τ and shift operator S_τ.

The subject function in Eq. (1) can be minimized via singular value decomposition (SVD) to update the patterns and its resulting coefficients [28]. When the pattern m_k is updated, the relevant shift operator S_τ is supposed to be fixed, and the pattern m_k and its coefficient x_k,τ are updated by the following equation:

     (5)

where is a set of all data indices using m_k in their representation and E^k represents overall error without the contribution of m_k. Finally, after the updated pattern m_k and its corresponding coefficient x_k,τ are obtained, the extracted impulse signal can be expressed as

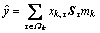                         (6)

2.2 Discussion of SI-K-SVD-related parameters

When SI-K-SVD is applied to gear-box bearing diagnosis, the proper selection of its two parameters, namely, the number of iterations and the pattern lengths, plays an important role in extracting fault information. The number of iterations is one of the key parameters in SI-K-SVD, which is expressed as nonzero entries of the sparse coefficients T₀. If the number of iterations is larger than the real number of impulses embedded in measured vibration signals, the false impulses without any fault information are extracted, whereas the ones with the fruitful fault information will be lost if the number of iterations is less than the real number of impulses. If the pattern length l is too short, the waveform of pattern is meaningless, whereas the learned pattern will contain a considerable amount of noise if the pattern length is too long.

The number of iterations is taken as an example to illustrate the importance of parameter selection. The simulated signals with an SNR of –5 dB are processed by SI-K-SVD with different number of iterations, and the results are shown in Figure 1. If the number of iterations is smaller than the real value, then the certain impulses, marked by green rectangles in Figure 1(a), will be missed. Conversely, the noisy components, indicated by red dash circles in Figure 1(c), are mistaken for fault impulses.

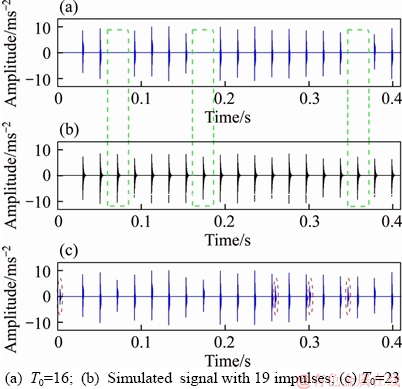
Figure 1 Extracted impulse signals using different numbers of iterations:

3 OP-SI-K-SVD

3.1 Indicator for selecting number of iterations

The number of iterations T₀ affects the distribution and sparseness of the extracted impulsive components. The SES is an effective indicator that reflects the sparseness of the extracted impulse signal [36]. The envelope spectrum of the signal is sparser when the extracted impulse signal has distinct periodic continuous impulses. Therefore, a higher SES value indicates that the extracted impulse signal has more periodic impulsive components and fewer non-periodic components. Hence, the SES value is used as an indicator to select the number of iterations.

The Hilbert transform h of the extracted impulse signal 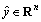is expressed as

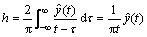                   (7)

The envelope spectrum (ES) ofis written as

                      (8)

where F{·} denotes the Fourier transform.

The SES is defined as [36]:

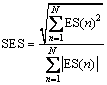                        (9)

The SES values for different numbers of iterations are computed and are shown in Figure 2(a). The SES has clear peak when T₀=19, which is equal to the number of impulses in the simulated signal. SI-K-SVD with T₀=19 can extract all of the fault impulsive components, as shown in Figure 2(b). As a result, the SES indicator is suitable for selecting the number of iterations. The procedure of selecting the number of iterations based on the SES is shown in Figure 3, where indicates that the number of iterations adopted in extracted impulse signal is i.

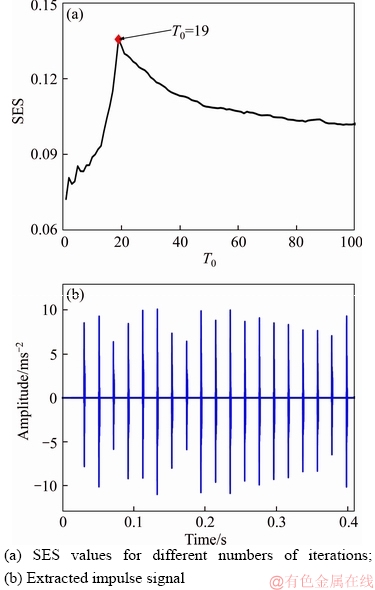
Figure 2 Selection of number of iterations based on SES:

3.2 Indicator for selecting pattern length

Another key parameter in SI-K-SVD is the pattern length l. The length of pattern should ideally be equal to the total length of the impulsive components. However, in practical application, the length of the impulse is unknown. The pattern length can typically be simply classified as shorter (less than half of the impulse attenuation) and longer (over half of impulse attenuation). To illustrate the influence of the different pattern lengths on the extraction of fault impulses, the simulated signals with a SNR of –12 dB are analyzed by SI-K-SVD with different pattern lengths. In the simulated signal, because the amplitudes of the impulses are small when the length of the impulse is larger than 48, the length of the impulse is considered to be 48. The results obtained by SI-K-SVD with different pattern lengths (36 and 12 sampling points) are shown in Figure 4 (the number of iterations is fixed at 19).

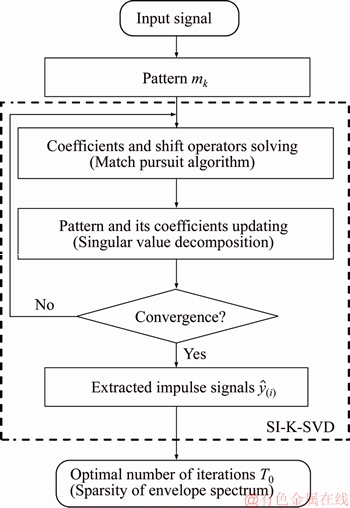
Figure 3 Procedure for selecting number of iterations based on SES

In Figure 4, SI-K-SVD with the two different pattern lengths can recognize the characteristic frequency of 48.6 Hz and its harmonics. Although two results have misrecognized components because of the heavy noises, 15 and 12 fault impulses are found by the shorter pattern and longer pattern, respectively. Compared to the envelope spectrums in Figure 4(d), the shorter pattern in Figure 4(b) can extract considerably more harmonics, and has better fault diagnosis property. The reason can be explained that the waveform with smaller amplitude in impulsive components will be easily masked by noise but the larger one is less influenced by noise.

Therefore, the pattern length must be properly selected in practical application. The KES is used to select the pattern length. The harmonics in the envelope spectrum imply the periodicity of the extracted impulse signal. More harmonics with higher amplitude appear in the envelope spectrum leading to considerably higher KES values [37]. Therefore, the KES can be employed as a suitable indicator for selecting the pattern length. The KES is expressed as [37]:

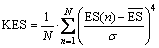                (10)

where is the average value of the envelope spectrum and σ is the standard deviation of the envelope spectrum.

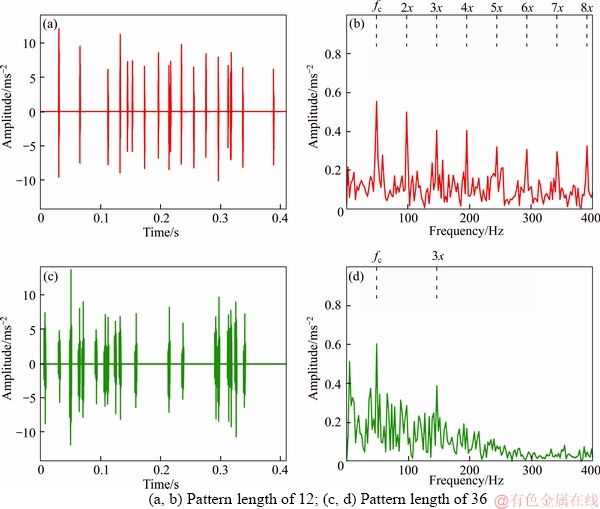
Figure 4 Extracted impulse signals (a, c) and its envelope spectrums (b, d) using different pattern lengths:

The KES values obtained for different pattern lengths are shown in Figure 5(a). The optimal pattern length is set as 8. The envelope spectrum of the extracted impulse signal using the optimal pattern length is shown in Figure 5(b). Therefore, the KES is an ideal indicator for selecting the pattern length. The procedure of the pattern length selection using the KES indicator is shown in Figure 6, where m_k(j) represents that the pattern length of m_k is j.

3.3 Procedure of OP-SI-K-SVD for fault diagnosis of a gear-box bearing

OP-SI-K-SVD for the fault diagnosis of a gear-box bearing mainly contains four steps, as shown in Figure 7.

Step 1: The optimal number of iterations T₀ is determined by the SES indicator;

Step 2: The optimal pattern length l is selected by the KES indicator;

Step 3: The optimal impulse signal generated by the gear-box bearing faults are extracted by the SI-K-SVD with the selected optimal T₀ and l.

Step 4: The envelope spectrum of the extracted impulse signal is used to assess the faults of a gear-box bearing.

4 Simulation validation

A bearing fault model that considers the effects of bearing geometry, load distribution, shaft speed and exponential decay vibration, etc., was proposed in a previous study [38], the model is expressed as:

Figure 5 Selection of pattern length based on KES:

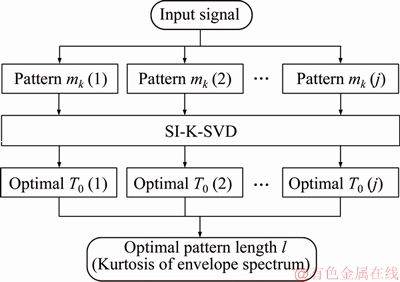
Figure 6 Procedure for selecting pattern length based on KES

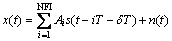               (11)

where NFI represents the number of fault impulses; A_i is the amplitude modulator with the period Q=1/f_m and written as

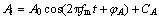                (12)

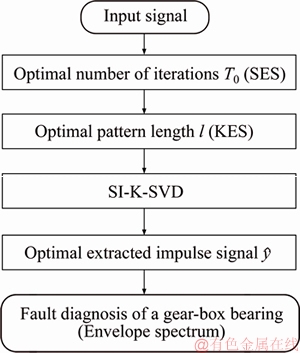
Figure 7 Procedure of OP-SI-K-SVD for fault diagnosis of a gear-box bearing

and s(t) is damping oscillation with mean impulse period T=1/f_c and is expressed as

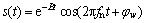                  (13)

and δT represents the random jitter caused by the sliding effect of rolling elements, which accounts for 1%–2% of T; n(t) is Gaussian-white-noise with zero-mean; f_n is the natural frequency of bearing system; A₀ is the resonance intensity; C_A is a constant; B is the coefficient of resonance damping; f_m is the nature frequency of the system; φ_A and φ_w are the initial phase.

The frequency parameters in the simulated signal are listed in Table 1, where f_c is the characteristic frequency and f₀ is the sampling rate. The simulated signal without any noises is shown in Figure 8. To test the performance of the proposed OP-SI-K-SVD under the conditions of different noise levels, two cases with medium and heavy noises are analyzed, respectively.

Table 1 Frequency parameters of simulation signal

4.1 Case 1: Simulation of a signal with a SNR of –5 dB (medium noises)

The simulated signal with a SNR of –5 dB is shown in Figure 9. The proposed OP-SI-K-SVD is used to extract impulsive components from the simulated signals. First, the SES and KES values are computed, as shown in Figures 10(a) and (b),respectively. According to the rules for selecting the number of iterations and pattern length, T₀ and l are equal to 19 and 12, respectively. The impulsive components extracted by OP-SI-K-SVD are shown in Figure 10(c), and their envelope spectrum is shown in Figure 10(d).

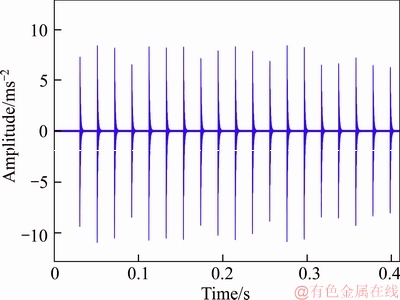
Figure 8 Time domain waveform of simulated signal without any noises

Compared to the envelope spectrum of simulated signal in Figure 9(c), the proposed OP-SI-K-SVD obtains a envelope spectrum with larger amplitudes of characteristic frequency, as shown in Figure 10(d), demonstrating that OP-SI-K-SVD can effectively extracte impulsive components and recognize the fault features.

4.2 Case 2: Simulation of a signal with a SNR of –12 dB (heavy noises)

The simulated signal with a SNR of –12 dB is shown in Figure 11. The Fourier spectrum of the simulated signal in Figure 11(b) and its envelope spectrum cannot discover obvious fault features. OP-SI-K-SVD is also employed to analyze the simulated signals. The SES and KES values for selecting the key parameters are computed and shown in Figures 12(a) and (b), respectively. As a result, T₀ and l are equal to 21 and 10, respectively. The impulsive components extracted by OP-SI-K-SVD are shown in Figure 12(c), and their envelope spectrum is shown in Figure 12(d).

Compared to the envelope spectrum of the simulated signal in Figure 11(c), the proposed OP-SI-K-SVD can obtain an envelope spectrum with larger amplitudes of harmonics and more harmonic number. This result demonstrates that OP-SI-K-SVD has excellent performance on recognizing the fault features, particularly under the heavy noise condition.

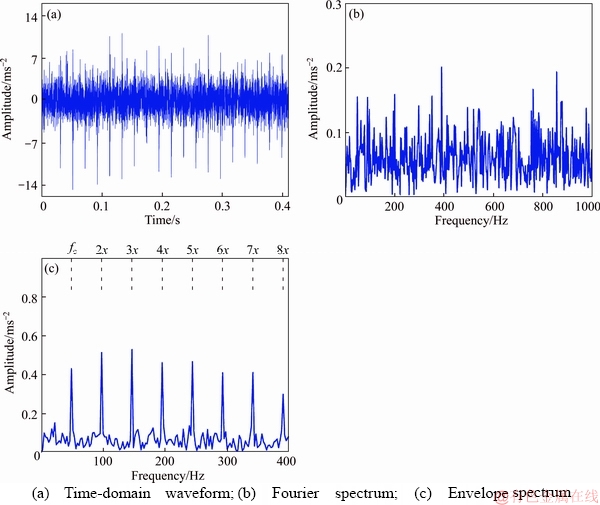
Figure 9 Simulated signals with a SNR of –5 dB:

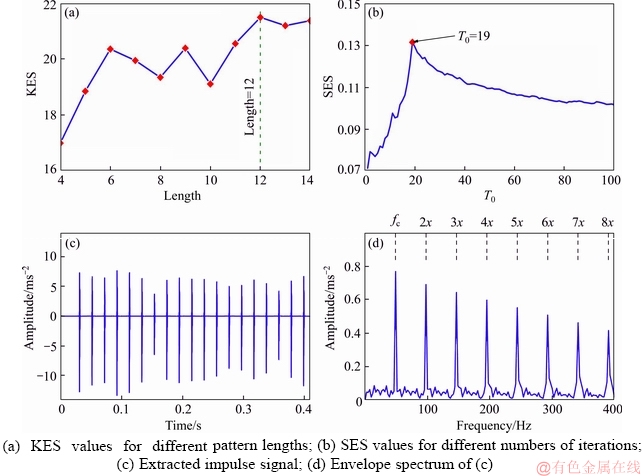
Figure 10 Results obtained by OP-SI-K-SVD under medium noise condition:

Figure 11 Simulated signals with a SNR of –12 dB:

5 Experimental study

An experimental bench is used to verify the proposed OP-SI-K-SVD, as shown in Figure 13(a). A single artificial defect on the surface of roller in Figure 13(b) is made using electro-discharge machining. The size of the defect is 0.1 mm, which is fairly small. The gear-box along with the single artificial defect on the roller surface of the bearing is used to conduct the fault experiments.

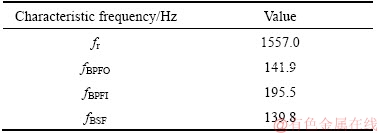
The detailed schematic diagram of the test bench is also shown in Figure 14. Accelerometers are installed on the input terminal of the shaft, and donated as c1 to c4. Because accelerometer c3 measures the vertical acceleration of the gear-box bearing, which can directly reflect effects of roller faults, the signal of c3 is selected to verify the performance of OP-SI-K-SVD. The rotation speed of the shaft is 1557 r/min corresponding to a train speed of 100 km/h. The vibration signals are collected at 10000 Hz. The geometric parameters of the gear-box input terminal bearing are listed in Table 2. The fault characteristic frequencies of bearing are computed according to the computation formulas [4], and are provided in Table 3, where f_r represents the rotation speed of the shaft, f_BPFO is the characteristic frequency of outer ring, f_BPFI is the characteristic frequency of inner ring and f_BSF is the characteristic frequency of roller.

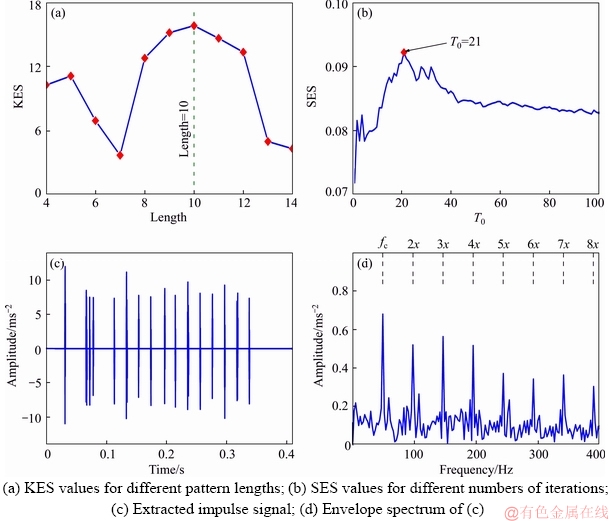
Figure 12 Results obtained by OP-SI-K-SVD under heavy noise condition:

Figure 13 Fault experiment of a gear-box bearing:

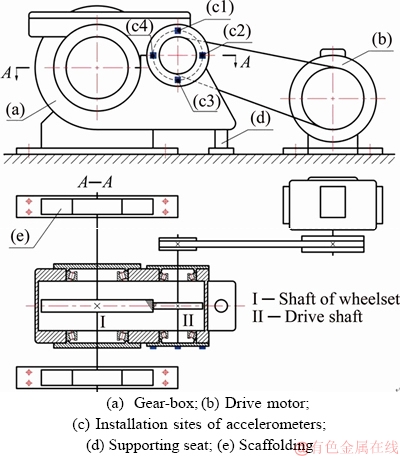
Figure 14 Test bench of a gear-box:

Table 2 Geometric parameters of gear-box input terminal bearing

Table 3 Characteristic frequencies

The measured vibration signal is shown in Figure 15(a). The envelope spectrum of raw sampled signal in Figure 15(c) cannot discover any characteristic frequencies or their harmonics.

Figure 15 Measured vibration signals:

Figure 16 shows the results obtained by the proposed OP-SI-K-SVD. The computed KES values and SES values are shown in Figures 16(a) and (b), respectively. The optimal pattern length and number of iterations are equal to 7 and 37, respectively. The extracted impulse signal and its envelope spectrum are shown in Figures 16(c) and (d), respectively. The envelope spectrum of extracted impulse signal shows that three highlighted spectrum lines corresponding to the roller fault characteristic frequency and its second and third harmonics are found using OP-SI-K-SVD.

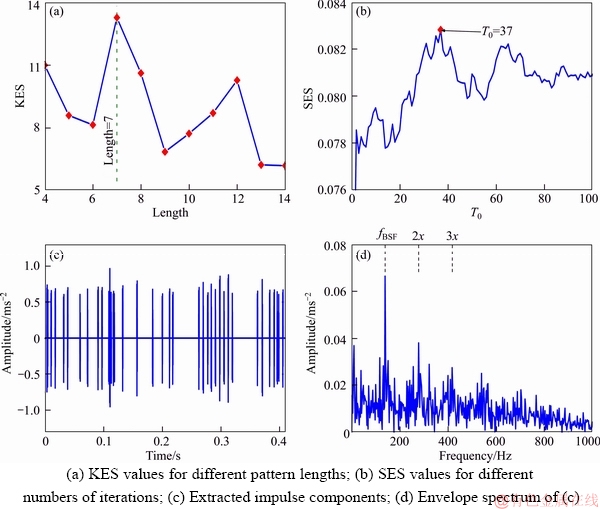
Figure 16 Results obtained by OP-SI-K-SVD:

To illustrate the superiority of the proposed OP-SI-K-SVD, three existing methods (EMD, WT, and K-SVD) are used to analyze the same measured signals in Figure 15(a). The results obtained using these three methods are shown in Figure 17. The IMF1, which has the highest correlation coefficient with the measured signals, is selected to extract fault information. The envelope spectrum of the IMF1 identifies the characteristic frequency of the roller fault and its second harmonic in Figure 17(b). However, these spectrum lines at the position of fault characteristic frequencies are masked by the noises. The “Coiflets” function is regarded as a basic WT function. The first-level decomposition signal in WT is shown in Figure 17(c). Its envelope spectrum in Figure 17(d) can only find the characteristic frequency of the roller fault. The time-domain waveform obtained by standard K-SVD is shown in Figure 17(e). Only the characteristic frequency of the roller fault can be found in the envelope spectrum, as shown in Figure 17(f). Compared to these three existing methods, OP-SI-K-SVD has better performance in diagnosing the faults of a gear-box bearing.

6 Conclusions

OP-SI-K-SVD is used to extract the high-level structure embedded in the measured vibration signals and detect the faults of a gear-box bearing. The high-level structure properly reflects the shift invariance of cyclic impulse action between faults and their matching surfaces. The SES and KES values are used as indicators to determine the number of iterations and pattern length, respectively.

Simulated and experimental signals are used to verify the effectiveness of the proposed OP-SI-K-SVD in the field of bearing fault diagnosis. Compared to three existing signal processing methods (EMD, WT and K-SVD), OP-SI-K-SVD is more suitable for extracting these weak fault impulsive components, and the proposed method has better performance in detecting the faults of a gear-box bearing.

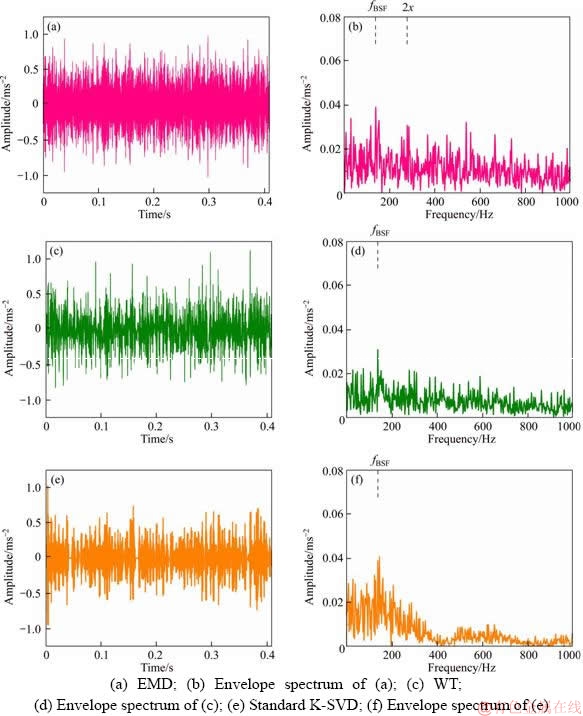
Figure 17 Results obtained by three comparison methods:

The types of the patterns embedded in the measured signals will be further discussed and estimated for complex fault detection.

References

[1] DONELSON J, DICUS R L. Bearing defect detection using on-board accelerometer measurement [C]// ASME/IEEE Joint Railroad Conference. Washington DC: IEEE, 2002: 95–102. DOI: 10.1109/ RRCON.2002.1000100.

[2] CAO Hong-rui, FAN Fei, ZHOU Kai, HE Zhen-jia. Wheel-bearing fault diagnosis of trains using empirical wavelet transform [J]. Measurement, 2016, 82: 439–449. DOI: 10.1016/j.measurement.2016.01.023.

[3] LEI Ya-guo, HE Zhen-jia, ZI Yan-yang, CHEN Xue-feng. New clustering algorithm-based fault diagnosis using compensation distance evaluation technique [J]. Mechanical Systems and Signal Processing, 2008, 22(2): 419–435. DOI: 10.1016/j.ymssp.2007.07.013.

[4] RANDALL R B, ANTONI J. Rolling element bearing diagnostics–A tutorial [J]. Mechanical Systems and Signal Processing, 2011, 25(2): 485–520. DOI: 10.1016/j.ymssp. 2010.07.017.

[5] ZHAO Ming, LIN Jing, MIAO Yong-hao, XU Xiao-qiang. Detection and recovery of fault impulses via improved harmonic product spectrum and its application in defect size estimation of train bearings [J]. Measurement, 2016, 91: 421–439. DOI: 10.1016/j. measurement. 2016. 05.068.

[6] ZHANG Xin-peng, HU Niao-qing, HU Lei, CHEN Ling. A bearing fault diagnosis method based on sparse decomposition theory [J]. Journal of Central South University, 2016, 23(8): 1961–1969. DOI: 10.1007/ s11771-016-3253-3.

[7] ASSAAD B, ELTABACH M, ANTONI J. Vibration based condition monitoring of a multistage epicyclic gearbox in lifting cranes [J]. Mechanical Systems and Signal Processing, 2014, 42(1, 2): 351–367. DOI: 10.1016/j.ymssp. 2013. 06. 032.

[8] MOSHER M. Understanding vibration spectra of planetary gear systems for fault detection [C]// ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. 2003: 645–652. DOI: 10.1115/DETC2003/PTG-48082.

[9] DONG Guang-ming, CHEN Jin. Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings [J]. Mechanical Systems and Signal Processing, 2012, 33(2): 212–236. DOI: 10.1016/j. ymssp. 2012.06.008.

[10] ZHAO De-zun, LI Jian-yong, CHENG Wei-dong, WANG Tian-yang. Rolling element bearing instantaneous rotational frequency estimation based on EMD soft-thresholding denoising and instantaneous fault characteristic frequency [J]. Journal of Central South University, 2016, 23(7): 1682–1689. DOI: 10.1007/ s11771-016-3222-x.

[11] LEI Ya-guo, HE Zhen-jia, ZI Yan-yang. EEMD method and WNN for fault diagnosis of locomotive roller bearings [J]. Expert Systems with Applications, 2011, 38(6): 7334–7341. DOI: 10.1016/j.eswa.2010.12.095.

[12] ZHAO Ming, LIN Jing, XU Xiao-qiang, LI Xue-jun. Multi-fault detection of rolling element bearings under harsh working condition using imf-based adaptive envelope order analysis [J]. Sensors, 2014, 14(11): 20320. DOI: 10.3390/s141120320.

[13] RAJIV K V, PENG Qing-jin. Crack detection in the rotor ball bearing system using switching control strategy and short time Fourier transform [J]. Journal of Sound and Vibration, 2018, 432: 502–529. DOI: https://doi.org/10.1016/j.jsv.2018. 06.061.

[14] XIE Ping, YANG Yu-xin, JIANG Guo-qian, LI Xiao-li. A new fault detection and diagnosis method based on Wigner-Ville spectrum entropy for the rolling bearing [J]. Applied Mechanics and Materials, 2012, 97: 346–350. DOI: 10.4028/www.scientific.net/amm.197.346.

[15] SUN Qiao, TANG Ying. Singularity analysis using continuous wavelet transform for bearing fault diagnosis [J]. Mechanical Systems and Signal Processing, 2002, 16(6): 1025–1041. DOI: 10.1006/mssp.2002.1474.

[16] LOU Xin-sheng, LOPARO K A. Bearing fault diagnosis based on wavelet transform and fuzzy inference [J]. Mechanical Systems and Signal Processing, 2004, 18(5): 1077–1095. DOI: 10.1016/s0888-3270(03)00077-3.

[17] PRABHAKAR S, MOHANTY A R, SEKHAR A S. Application of discrete wavelet transform for detection of ball bearing race faults [J]. Tribology International, 2002, 35(12): 793–800. DOI: 10.1016/S0301-679X (02)00063-4.

[18] KAR C, MOHANTY A R. Monitoring gear vibrations through motor current signature analysis and wavelet transform [J]. Mechanical Systems and Signal Processing, 2006, 20(1): 158–187. DOI: 10.1016/j.ymssp.2004.07.006.

[19] PENG Zhi-ke, CHU Fu-lei. Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography [J]. Mechanical Systems and Signal Processing, 2004, 18(2): 199–221. DOI: 10.1016/s0888-3270(03)00075-x.

[20] HAN Te, JIANG Dong-xiang, ZHANG Xiao-chen, SUN Yan-kui. Intelligent diagnosis method for rotating machinery using dictionary learning and singular value decomposition [J]. Sensors, 2017, 17(4): 689. DOI: 10.3390/ s17040689.

[21] DING Jian-ming. Fault detection of a wheelset bearing in high-speed train using the shock-response convolutional sparse-coding technique [J]. Measurement, 2018, 117: 108–124. DOI: 10.1016/j.measurement.2017.12.010.

[22] MAIRAL J, BACH F, PONCE J, SAPIRO G. Online dictionary learning for sparse coding [C]// International Conference on Machine Learning, ICML 2009. Montreal, Quebec, Canada, 2009: 689–696. DOI: 10.1145/ 1553374.1553463.

[23] ENGAN K. AASE S O, HUSOY J H. Method of optimal directions for frame design [C]// IEEE International Conference on Acoustics, Speech, and Signal Processing. 1999: 2443–2446. DOI: 10.1109/ICASSP.1999.760624.

[24] AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation [J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311–4322. DOI: 10.1109/TSP.2006.881199.

[25] RUBINSTEIN R, PELEG T, ELAD M. Analysis K-SVD: A dictionary-learning algorithm for the analysis sparse model [J]. IEEE Transactions on Signal Processing, 2013, 61(3): 661–677. DOI: 10.1109/TSP.2012.2226445.

[26] ENGAN K, SKRETTING K, HUSY J H. Family of iterative LS-based dictionary learning algorithms, ILS-DLA, for sparse signal representation [J]. Digital Signal Processing, 2007, 17(1): 32–49. DOI:10.1016/j.dsp.2006.02.002.

[27] WOHLBERG B. Efficient algorithms for convolutional sparse representations [J]. IEEE Transactions on Image Processing, 2015, 25(1): 301–315. DOI: 10.1109/tip. 2015.2495260.

[28] MAILH B, LESAGE S, GRIBONVAL R, BIMBOT F, VANDERGHEYNST P. Shift-invariant dictionary learning for sparse representations: Extending K-SVD [C]// Signal Processing Conference. European IEEE, 2008: 1–5. DOI: https://ieeexplore.ieee.org/document/7080585.

[29] GROSSE R, RAINA R, KWONG H, NG A Y. Shift-invariance sparse coding for audio classification [J]. Computer Science, 2012, 6: 149–158. DOI: https://arxiv.org/ abs/1206.5241v1.

[30] ZHENG Guo-qing, YANG Yi-ming, CARBONELL J. Efficient shift-invariant dictionary learning [C]// ACM Sigkdd International Conference. 2016: 2095–2104. DOI: 10.1145/2939672.2939824.

[31] FENG Zhi-peng, LIANG Ming. Complex signal analysis for planetary gearbox fault diagnosis via shift invariant dictionary learning [J]. Measurement, 2016, 90: 382–395. DOI: 10.1016/j.measurement.2016.04.078.

[32] ELAD M, STRACK J L, QUERRE P, DONOHO D L. Simultaneous cartoon and texture image inpainting using morphological component analysis (MCA) [J]. Applied and Computational Harmonic Analysis, 2005, 19(3): 340–358. DOI: 10.1016/j.acha.2005.03.005.

[33] WERSING H, EGGERT J, KRNER E. Sparse coding with invariance constraints [J]. Artificial Neural Networks and Neural Information Processing–ICANN/ICONIP, 2003, 2714: 385–392. DOI: 10.1007/3-540-44989-2_46.

[34] THIAGARAJAN J J, RAMAMURTHY K N, SPANIAS A. Shift-invariant sparse representation of images using learned dictionaries [C]// Proceedings of IEEE Workshop on Machine Learning for Signal Processing. 2008: 145–150. DOI: 10.1109/MLSP.2008.4685470.

[35] KRSTULOVIC S, GRIBONVAL R. MPTK: Matching pursuit made tractable [C]// IEEE International Conference on Acoustics Speech & Signal Processing IEEE, 2006, 3: 496–499. DOI: 10.1109/ICASSP.2006.1660699.

[36] TSE P W, WANG Dong. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement-Parts 1 and 2” [J]. Mechanical Systems and Signal Processing, 2013, 40(2): 499–519. DOI: 10.1016/j.ymssp.2013.05.024.

[37] McDONALD G L, ZHAO Qing, ZUO Ming-jian. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection [J]. Mechanical Systems and Signal Processing, 2012, 33(1): 237–255. DOI: 10.1016/j.ymssp. 2012.06.010.

[38] MCFADDEN P D, SMITH J D. The vibration produced by multiple point defects in a rolling element bearing [J]. Journal of Sound and Vibration, 1985, 98(2): 263–273. DOI: 10.1016/0022-460x (85)90390-6.

(Edited by FANG Jing-hua)

中文导读

移不变字典学习算法提取冲击成分及其在齿轮箱轴承早期故障诊断中的应用

摘要：由轴承故障所产生的故障冲击成分是对齿轮箱轴承故障评估的关键特征。但是由于严重的背景噪声与其它振动的干扰，从测量的振动信号中提取这些故障尤其是早期故障的冲击成分是十分困难的。为了捕捉到这些隐藏在测量的振动信号中的冲击成分的高阶特征，应用一种被称作移不变K均值奇异值分解字典学习算法(SI-K-SVD)对齿轮箱轴承进行早期故障检测。尽管移不变K均值奇异值分解字典学习算法比现有的大部分算法更具有灵活性与自适应性，但与该算法密切相关的两种参数（迭代次数与模式的长度）的不合理选取，会对故障诊断的效果产生负面影响。因此，该算法引入包络谱的稀疏度与峭度值并分别用于选取上述两种参数。基于这两种参数优化选取的移不变K均值奇异值分解字典学习算法，被称为最优参数移不变奇异值分解字典学习算法(OP-SI-K-SVD)，本文采用该算法用于齿轮箱轴承的故障检测。通过对仿真与台架试验的数据的分析，验证了该算法的有效性。同时通过与现有的几种先进算法(经验模态分解、小波变换和K均值奇异值分解)的对比，最优参数移不变奇异值分解字典学习算法在齿轮箱轴承的早期故障诊断中展现出了优异的性能。

关键词：齿轮箱轴承；故障诊断；移不变K均值奇异值分解字典学习算法；冲击成分提取

Foundation item: Project(51875481) supported by the National Natural Science Foundation of China; Project(2682017CX011) supported by the Fundamental Research Foundations for the Central Universities, China; Project(2017M623009) supported by the China Postdoctoral Science Foundation; Project(2017YFB1201004) supported by the National Key Research and Development Plan for Advanced Rail Transit, China; Project(2019TPL_T08) supported by the Research Fund of the State Key Laboratory of Traction Power, China

Received date: 2018-03-29; Accepted date: 2018-11-18

Corresponding author: DING Jian-ming, PhD, Associate Professor; Tel: +86-13880454258; E-mail: fdingjianming@126.com; ORCID: 0000-0003-4565-0042