Testing study of subcritical crack growth rate and fracture toughness in

different rocks

CAO Ping(曹 平), LI Jiang-teng(李江腾), YUAN Hai-ping(袁海平)

School of Resources and Safety Engineering, Central South University, Changsha 410083, China

Received 28 February 2005; accepted 1 June 2005

Abstract: Subcritical crack growth of double torsion specimens made of ore, lherzolite, marble and granite was studied using Instron1342 type electro hydraulic servo test machine. The relations of the mode-I stress intensity factor K_I versus the subcritical crack growth velocity v and the fracture toughness K_IC were obtained by the double torsion constant displacement load relaxation method. The behavior of subcritical crack growth was analyzed for different rocks. The results show that lgK_I—lgv relations of four kinds of rocks measured by this method accord with linear rule, i.e. the relations between subcritical crack growth velocity and stress intensity factor have a power law, which is in good agreement with CHARLES theory. lgK_I—lgv curves move to top left corner with the decrease of the elastic modulus, which implies that the subcritical crack growth velocity speeds up. The maximum subcritical crack growth velocity exhibits negative exponential increase, and mode-I fracture toughness K_IC decreases with the decrease of elastic modulus. The testing results provide a basis for time-dependence of rock engineering stability.

Key words: rocks; fracture toughness; subcritical crack growth; double-torsion specimens; constant displacement load relaxation method

1 Introduction

The time effect of rock engineering stability is attached importance to with enlarging of the rock engineering scale. The instability instances in-situ and rock laboratory examinations show that the rock instability is owing to crack growth, propagation, encounter and integrating in rock mass. The fracture mechanics method has been adopted to study crack growth laws in rock mass in 30 years[1-6]. The research shows that the cracks in environmental medium material propagate until material fractures under combined action of tensile stress and corrosion medium, which is called stress corrosion. Usually, the mode-I stress intensity factor K_I at crack tip is regarded as a parameter to control the crack growth. The stress corrosion lower limit is K₀, and the fracture toughness is K_IC. When K_I>K_IC, the crack grows catastrophically at velocity of sound approximatively, and when K_I0, the crack does not grow, and when K₀IIC, the crack grows at a certain velocity and increases with the stress intensity factor K_I. The reasons may be listed as follows[7]: 1) The stresses at crack tip increase in the process of forming micro-crack and interspace; 2) The chemical bond fracture stresses decrease by the effects of environmental medium. But the crack grows at stability and static state in the process, which is called subcritical crack growth. The crack grows catastrophically in rock mass and engineering instability happens after the subcritical cracks propagate to a certain extent, which results in that rock engineering instability relates to crack growth time. So, studies of the subcritical crack growth laws and fracture properties and their testing data are important to rock engineering long-term stability.

The principle of testing subcritical crack growth velocity, the mode-I stress intensity factor K_I and the fracture toughness K_IC were introduced using double torsion specimens in the paper. Subcritical crack growth of double torsion specimens made of ore, lherzolite, marble and granite was studied using Instron1342 type electro hydraulic servo test machine. The relations of the mode-I stress intensity factor K_I versus the subcritical crack growth velocity v and the fracture toughness K_IC were obtained by the double torsion constant displacement load relaxation method. The behavior of subcritical crack growth was analyzed in different rocks. The testing results provide basis for time-dependency of rock engineering stability.

2 Principle of double torsion testing

The specimen of double torsion is shown in Fig.1, which is a rectangle plate. There is a longitudinal groove on the bottom surface, and the crack front proceeds along a straight line starting from a machined initial notch and guided by a side groove thus producing a relaxation of the load. The specimen is treated as two elastic torsion bars. According to Refs.[8-13], the stress intensity factor K_I and the subcritical crack growth v can be obtained for small deformation when the width of torsion bar is much larger than its thickness (see Eq.(1) and Eq.(2)).

                       (1)

                   (2)

where  P is the applied load, w_m is the moment arm of the torsion, ν is Poisson’s ratio, d is the thickness of the specimen, d_n is the thickness of the specimen minus the groove depth, W/2 is the width of torsion bar, E is elastic modulus, and t is time.

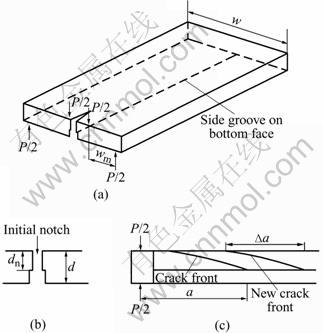
Fig.1 Schematic diagram of double torsion specimen:       (a) Specimen shape; (b) Cross-section in width; (c) Cross- section in length

Crack will propagate catastrophically when P comes up to critical P_C, i.e. K_I is equal to the fracture toughness K_IC.

                      (3)

It can be seen that the stress intensity factor K_I and subcritical crack growth rate are independent of the crack length, which is very useful in the subcritical crack growth research. The relation between the subcritical crack growth v and the stress intensity factor K_I can be established by Eq.(1) and Eq.(2).

3 Experimental

3.1 Sample preparation

Four kinds of rocks from Jinchuan Mining Area are machined as rectangle plate double torsion specimens, There is a longitudinal groove on the bottom surface, which is 1 mm in width and t/3 in depth, and a notch is cut at the end. The crack front proceeds along a straight line starting from a machined initial notch and guided by a side groove thus producing a relaxation of the load. The parallel error between the top surface and the bottom surface of specimens is less than 0.025 mm[14]. The specimens size and mechanical parameters are listed in Table 1.

3.2 Testing methods

The advantage of this method is that it only requires one to monitor the decrease of the load with time to measure both the stress intensity factor K_I and the subcritical crack growth velocity v, without any need to measure the crack length during the testing. Furthermore, pre-crack method is simple and effective, so, it has been effective means in the subcritical crack growth research. The testing was processed using Instron1342 type electro hydraulic servo test machine in the testing center of Central South University. The specimens should be pre-cracked to obtain reasonable K_IC and K_I—v data[3, 9, 14], and pre-crack velocity is 0.05 mm/min. The load-time curve of typical specimen in pre-crack is shown in Fig.2.There is a turning point in the curve, and the drop in load is interpreted as the initiation of pre- crack.

Table 1 Specimens size and mechanical parameters

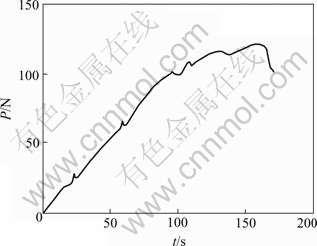
Fig.2 Load—time curve of typical specimen in pre-crack

The pre-cracked specimen is loaded in 5 mm/min displacement velocity during constant displacement load relaxation testing[9] firstly, and the displacement of specimen is kept to constant when the load comes up to 95%[6, 15]of pre-crack load and the relaxation testing is done. The load-time data are recorded until load relaxation is stabilized. The load-time curve and the displacement-time curve of typical specimen are shown in Fig.3 and Fig.4 respectively. The normalized load-time curve of typical specimens of four kinds of rocks are shown in Fig.5

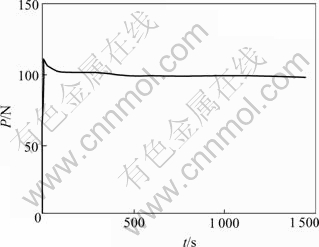
Fig.3 Load—time curve of typical specimen

The pre-cracked specimen is loaded in 20mm/min displacement velocity during the fracture toughness K_IC testing[9, 14], and record critical load P_c. The fracture toughness K_IC can be obtained by Eqn.(12). The load— time curve of typical specimen in testing K_IC is shown in Fig.6.

4 Results and analysis

According to the testing data, the relation between the subcritical crack growth v and the stress intensity factor K_I of four kinds of rocks can be established by Eqn.(1) and Eqn.(2), and their average logK_I—logv coordinate points in logarithm coordinates are shown in Fig.7. logK_I—logv data are regressed as

                            (4)

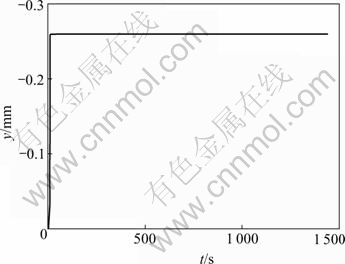
Fig.4 Displacement—time curve of typical specimen

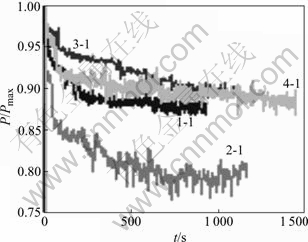
Fig.5 Normalized load—time curve of typical specimens of four kinds of rocks

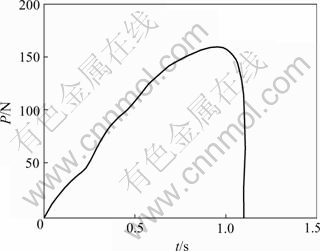
Fig.6 Load—time curve of typical specimen in testing K_IC

The mechanical parameters of rocks differ from each other, and the load P depends on the mechanical parameters in Eqn.(1) and Eqn.(2). It can be seen that the subcritical crack growth velocity is visible function of the elastic modulus E besides the load P. So, the elastic modulus E is employed to reveal the subcritical crack growth velocity laws in different rocks.

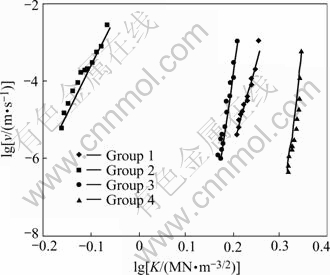
Fig.7 Average K_I—v curve of four kinds of rocks

The average K_I—v curves of four kinds of rocks are shown in Fig.7. It can be seen that the curves move to top left corner with decrease of the elastic modulus E, which implies that the subcritical crack growth threshold and the fracture toughness decrease, but the subcritical crack growth velocity speeds up.

The subcritical crack growth ranges are different in four kinds of rocks. The elastic modulus E is minimum in lherzolite and the maximum of the subcritical crack growth velocity is 10^{-3 m}/s scale. But, the elastic modulus E is maximum in granite and the maximum of subcritical crack growth velocity is 10^{-4 m}/s scale, and its subcritical crack growth velocity is less than that in lherzolite. It can be seen that the maximum subcritical crack growth velocity increases with decrease of elastic modulus E from Table 2, and that the maximum subcritical crack growth velocity exhibits negative exponential increase with decrease of elastic modulus E from Fig.8. The minimum subcritical crack growth velocity depends on relaxation time besides components in rock, and the longer the relaxation time, the less the subcritical crack growth minimum velocity.

The ability of resisting crack growth strengthens with increasing elastic modulus E, i.e. the fracture toughness increases accordingly in theory. The parameparameters of subcritical crack growth and fracture toughness (average) of four kinds of rocks are listed in Table 3. The relations between the mode-I fracture toughness K_IC and elastic modulus E are shown in Fig.9. It can be seen that the fracture toughness increases with the elastic modulus E increasing, which accords with theory.

Table 2 Velocity v and stress intensity factor K_I (average)

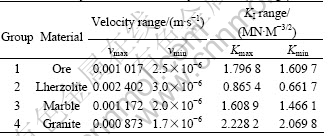
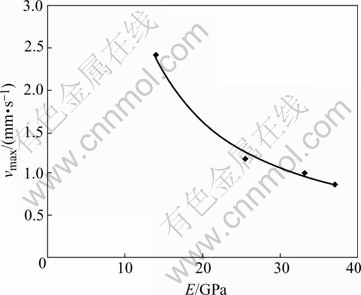
Fig.8 Subcritical crack growth maximal velocity v_max vs elastic modulus E

Table 3 Parameters of subcritical crack growth and fracture toughness (average)

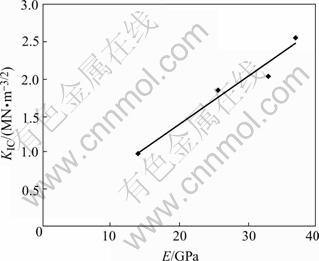
Fig.9 Mode-I fracture toughness K_IC vs elastic modulus E

5 Conclusions

1) Subcritical crack growth of double torsion specimens made of ore, lherzolite, marble, granite was studied using Instron1342 type electro hydraulic servo test machine. The relations of the mode-I stress intensity factor K_I versus the subcritical crack growth velocity v and the fracture toughness K_IC were obtained by the double torsion constant displacement load relaxation method. The behavior of subcritical crack growth was analyzed in different rocks.

2) lgK_I—lgv relations of four kinds of rocks measured by this method accord with linear rule, i.e., the relations between subcritical crack growth velocity v and stress intensity factor K_I have power law, which is in good agreement with CHARLES theory.

3) lgK_I—lgv curves move to top left corner with decrease of the elastic modulus E, which implies that the subcritical crack growth velocity speeds up, and the fracture toughness K_IC decreases, which accords with practice.

4) The subcritical crack growth ranges are different in four kinds of rocks, and it is within 10^-3-10^{-8 m}/s scale. The maximum subcritical crack growth velocity exhibits negative exponential increase with decrease of elastic modulus E and the minimum subcritical crack growth velocity depends on relaxation time besides components in rock, and the longer the relaxation time, the less the subcritical crack growth minimum velocity.

References

[1] Williams D P, Evans A G. A simple method for studying slow crack growth [J]. Journal of Testing and Evaluation, 1973, 1(4): 264-270.

[2] Henry J P, Paquet J, Tancret J P. Experimental study of crack propagation in calcite rocks [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1977 ,14(1): 85-91.

[3] Atkinson B K. Fracture toughness of Tennessee sandstone and Canam marble using the double torsion testing method [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1979, 16(1): 49-53.

[4] Swanson P L. Subcritical crack propagation in westerly granite: an investigation into the double torsion method [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1981, 18(2): 445-449.

[5] XIAO Hong-tian. Rheologic damage study of three gorges shiplock highslope and analysis on in-situ measured deformation [J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(5): 497-502.(in Chinese)

[6] Ciccotti m, Negri n, Sassi l, et al. Elastic and fracture parameters of Etna, Stromboli, and Vulcano lava rocks [J]. Journal of Volcanology and Geothermal Research, 2000, 98(1-4): 209-217.

[7] ZHANG Fu-fan, WANG Fu-chu, LU Jian. Fracture mechanics [M]. Beijing: China Architecture & Building Press, 1981.(in Chinese)

[8] SUN Shun-fang. Material Mechanics [M]. Beijing: People Education Press, 1979.(in Chinese)

[9] Saadaouia m, Reynauda p, Fantozzia g, et al. Slow crack growth study of plaster using the double torsion method [J]. Ceramics International, 2000, 26(4): 435-439.

[10] Chevalier j, Olagnon c, Fantozzia g, et al. Subcritical crack growth and thresholds in a 3Y-TZP ceramin under static and cyclic loading conditions [J]. Ceramics International, 1997, 23(3): 263-266.

[11] Krella a, Pippelb e, Woltersdorf j, et al. Subcritical crack growth in Al₂O₃ with submicron grain size [J]. Journal of the European Ceramic Society, 2003, 23(1): 81-89.

[12] Ciccotti m, Gonzato g, Mulargia f. The double torsion loading configuration for fracture propagation: an improved methodology for the load-relaxation at constant displacement [J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(7): 1103-1113.

[13] Ciccotti m, Negri n, Gonzato g, et al. Practical application of an improved methodology for the double torsion load relaxation method [J]. International Journal of Rock Mechanics & Mining Sciences, 2001, 38(4): 569-576.

[14] YU Xiao-zhong. Fracture Mechanics of Rock and Concrete [M]. Changsha: Central South University of Technology Press, 1991.(in Chinese)

[15] Ebrahimi M E, Chevalier J, Fantozzi G. Slow crack growth behavior of alumina ceramics [J]. J Master Res, 2000, 15(1): 142-147.

Foundation item: Project(50274074) supported by the National Nature Science Foundation of China; Key Project(50490274) supported by the National Nature Science Foundation of China

Corresponding author: CAO Ping; Tel: +86-731-8879612; E-mail: pcao_csu@sohu.com

(Edited by PENG Chao-qun)