­­ Study of thermal expansion of mercury indium telluride crystals by XRD technique

WANG Ling-hang (王领航)¹, JIE Wan-qi(介万奇)²

1. Electronic Materials Research Laboratory, Key Laboratory of Education Ministry,

Xi’an Jiaotong University, Xi’an 710049, China;

2. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China

Received 10 August 2009; accepted 15 September 2009

Abstract: The thermal expansion behavior of mercury indium telluride (MIT) crystals, Hg_(3-3x)In_2xTe₃(x=0.5), based on X-ray diffraction experimental data is studied at 298-573 K. The variation of the lattice parameter of MIT crystals with temperature was determined and the thermal expansion coefficient was deduced to be 6.18×10^-6 K^-1. The results of the thermal expansion are fitted to polynomial expressions. It is found that the lattice parameter decreases quickly with temperature increasing at 298-330 K and then increases continuously up to 573 K. The minimum lattice parameter corresponds to a maximum shrinkage of 0.06%.

Key words: mercury indium telluride; crystal growth; XRD; thermal expansion; semiconductor material

1 Introduction

Solid solutions of Ⅱ-Ⅵ/Ⅲ-Ⅵ system attract many scientists due to their special feature of the high concentration of the structural vacancies[1-4]. Mercury indium telluride (MIT) with the formula of Hg_(3-3x)In_2xTe₃ in HgTe/In₂Te₃ system is disclosed to be one of the important novel Ⅱ-Ⅵ/Ⅲ-Ⅵ compounds. For Hg_(3-3x)In_2xTe₃, three stable phases are known at x=0.375, x=0.5 and x=0.75 called β, α₂ and γ, respectively[5]. β phase has a body-centered tetragonal structure. It undergoes a transition from ordered structure to partially ordered structure at 720 K[6] and reacts peritectically with α₂ and γ at 973 K[5]. α₂ phase is face-centered cubic and its structure is related to that of the zinc-blende type ZnS. At 585 K, α₂ undertakes an order-disorder transformation[7]. It has been reported that α₂ completely decomposes to In₂Te₅ and In₃Te₅ with Hg escaped at 661 K at open condition[8]. The melting point of α₂ is 982 K[9]. γ phase belongs to the chalcopyrite structure and melts congruently at 982 K[10]. Among them, MIT (x=0.5) is considered as a promising material for fast and efficient near-infrared photodetectors[11]. Information on thermal expansion coefficient and thermal conductivity of MIT as a function of temperature is essential to evaluate the thermophysical properties under temperature gradients. So far, no details concerning the thermal expansion behavior of MIT crystals studied by XRD technique were reported. Therefore, thermal expansion investigation was carried out for MIT (x=0.5) compound of HgTe-In₂Te₃ system. The aim of the present work is to study the thermal expansion behavior of MIT (x=0.5) compound as a function of temperature.

2 Experimental

The sample of MIT single crystal was grown by using the vertical Bridgman (VB) method[12-13]. The raw materials for crystal growth were synthesized by direct reaction in vacuum in a quartz ampoule using the high purity (99.999 99%) elements of Te, In and Hg. The crystal growth was performed in a vertical Bridgman furnace in the same ampoule. A temperature gradient of 10 K/cm and a growth rate of less than 1 mm/h were adopted. The ingot was in-situ annealed for 72 h after growth.

Phase identification and crystal structure of the as-grown crystals was examined by X-ray powder diffraction (XRPD) method. In order to monitor the crystal structure of MIT material, high temperature X-ray diffraction (HT-XRD) measurements were carried out at 298-573 K. The HT-XRD patterns were taken at an interval of 50 K using a high temperature attachment. The sample cut from the as-grown crystal was crushed and finely ground into powder, then mixed with drops of acetone and well distributed on a Pt-Rh sample carrier, which is spot welded at the bottom with a Pt/Pt-10%Rh thermocouple to collect temperature signals. The programmed heating rate was set to 5 ℃/min. An X′Pert MPO Pro X-ray diffractometer was employed to record the diffraction data in the 2θ range of 10?-120? with the step of 0.033 0?. The X-ray source was Cu K_α with the wavelength of 0.154 060 nm. The accelerating voltage was 40 kV and the current was 35 mA. Divergence slit and the recieving slit were 0.435 4? and 0.05?, respectively. The lattice parameters at each temperature were determined by using a computer DICVOL program with an accuracy of ±1.0×10^-5 nm.

3 Results and discussion

The thermal expansion of a crystal implied by the thermal-expansion coefficient has great influence on crystal growth and on its possible applications. It is known that the thermal-expansion coefficient is a symmetrical second-rank tensor and can be geometrically described by a second-rank indicative surface, which can be expressed in the principal axis coordinate by the following form[14-15]:

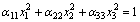                      (1)

where the semi-axis lengths of the three principal axes of the second-rank indicative surface are (α₁₁)^-1/2, (α₂₂)^-1/2, and (α₃₃)^-1/2. The shape of the second-rank indicative surface is determined by the values of the principal components (α₁₁, α₂₂ and α₃₃). The thermal expansion coefficient tensor with respect to the axes in the principal coordinate is

                         (2)

For MIT (x=0.5) crystal, it has a defect zinc-blende structure and belongs topoint group[12], which has four triad axes along the diagonal of the crystallographic lattice and three diad axes along the crystallographic axes that are selected as the axes in the principal coordinate. According to the Neumann’s principle, the components of the thermal-expansion coefficient tensor can be calculated to be only one independent principal component (α₁₁=α₂₂=α₃₃). The second-rank indicative surface of MIT crystal has three equal semi-axis lengths and is a sphere.

In order to determine the value of α₁₁, the thermal expansion of MIT crystal by HT-XRD method was measured. The HT-XRD patterns up to 573 K clearly display the shift in the X-ray diffraction line positions showing the change of the unit cell. The XRD pattern at room temperature of MIT crystal is shown in Fig.1, from which the unit cell parameters are determined to be  0.629 34 nm with a volume of 0.249 26 nm³. Fig.2 shows the variation of lattice parameters of MIT crystal with temperature at 298-573 K. It can be seen that the lattice parameter of MIT crystal decreases with temperature at the first stage, then increases continuously up to 573 K. The volume of the unit cell has the same trend. The lattice parameter inclines quickly at a ratio of about 1.52×10^-5 nm/K in the shrinkage stage, and then begins to expand. At the expansion stage, the expansion ratio reduces to about 5.8 ×10^-6 nm/K. The thermal expansion behavior of MIT crystal exhibits a minimum in the expansion curve. The shrinkage is probably caused by removal of the residual thermal defects formed during the cooling process when MIT crystals are quenched.

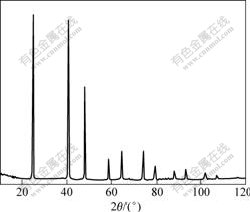
Fig.1 XRD pattern of MIT (x=0.5) crystal at room temperature

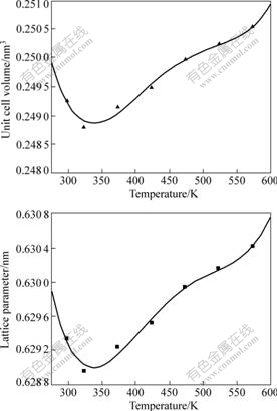
Fig.2 Variations of lattice parameter of MIT (x=0.5) crystal with temperature

The lattice parameter of MIT crystal against temperature can be probably expressed by a fourth-order polynomial relation obtained from the least squares method as implied by Eqns.(3)-(4):

a_T=0.709 66-0.000 74T+0.250 17×10^-5T²–

0.365 85×10^-8T³+0.197 74×10^-11T⁴          (3)

V_T=345.941 1×10^-3-0.894 2×10^-3T+0.003 0×10^-3T²-

4.408 3×10^-9T³+2.383 2×10^-12T⁴            (4)

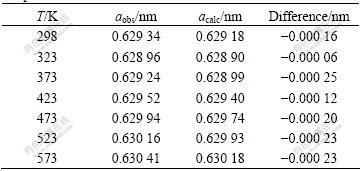
The theoretical temperature corresponding to the minimum lattice parameter was determined to be 330 K from the differential results of ?a/?T=0. The values of the lattice parameters observed and calculated from Eqn.(3) are both given in Table 1. The total error of the individually observed lattice parameter is probably no more than 0.000 2 nm. Eqn.(3) is taken as a better representation of the results.

Table 1 Lattice parameters of MIT crystals at different temperatures

The values of the thermal expansion coefficient can generally be obtained by the expression of α=       (1/a) (?a/?T) from the relation of lattice parameter a and temperature T. Supposing that the lattice parameter of MIT crystal at 298 K is a₂₉₈, the value of the thermal expansion coefficient (α_T) can be calculated through the following equation:

                              (5)

where Δa is the variation of lattice parameter corresponding to a temperature change ΔT. The value of the average thermal expansion coefficient at 298-573 K can be theoretically calculated from Eqn.(5) to be α₁₁=6.18×10^-6 K^-1. The volume coefficient of thermal expansion is equal to 18.54×10^-6 K^-1.

Fig.3 shows the thermal expansion coefficients of MIT crystal at 298-573 K. It is noticeable for the thermal expansion behavior of MIT crystal that there are two distinctive parts: shrinkage and expansion stages. The thermal expansion coefficient of the former is up to -24.15×10^-6 K^-1, whereas that of the latter is 9.22×10^-6 K^-1.

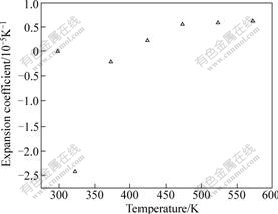
Fig.3 Thermal expansion coefficient of MIT (x=0.5) crystal

The distinctive thermal expansion behavior suggests that in the process of MIT crystal growth, different cooling rates should be adopted; otherwise, a large amounts of defects are likely to be introduced into the crystal, such as microcracks.

4 Conclusions

1) The thermal expansion behavior of mercury indium telluride (MIT) crystals, Hg_(3-3x)In_2xTe₃ (x=0.5), grown by vertical Bridgman (VB) method was studied at 298-573 K by the high temperature X-ray diffraction (HT-XRD) measurements. It is found that the unit cell of MIT shrinks quickly with temperature increasing at 298-330 K and then expands continuously up to 573 K. There exists a maximum shrinkage of 0.06% at 330 K.

2) The lattice parameters of MIT crystal are fitted to a fourth-order polynomial expression as a function of temperature. There are two distinctive parts in the expansion curve of MIT crystals: shrinkage and expansion stages. The thermal expansion coefficient at the former stage is up to -24.15×10^-6 K^-1, whereas that at the latter stage is 9.22×10^-6 K^-1. The average thermal expansion coefficient is 6.18×10^-6 K^-1 at 298-573 K.

References

[1] WOOLLEY J C, RAY B. Effects of solid solution of In₂Te₃ with A^ⅡB^Ⅵ tellurides [J]. J Phys Chem Solids, 1960, 15: 27-32.

[2] HAILING T, SAUNDERS G A, LAMBSON W A. Elastic behaviour under pressure of the vacancy compounds [J]. Phys Rev B, 1982, 26(10): 5786-5797.

[3] SAUNDERS G A, SEDDON T. The elastic behaviour of tetrahedral materials with vacant sites [J]. J Phys Chem Solids, 1976, 37: 873-882.

[4] GASTALDI L, SIMEONE M G , VITICOLI S. Cation ordering and crystal structures in AGa₂X₄ compounds [J]. Solid State Communication, 1985, 55(7): 605-607.

[5] SPENCER P M, RAY B. Phase diagram of the alloy system Hg₃Te₃-In₂Te₃ [J]. Brit J Appl Phys (J Phys D), 1968, 1: 299-301.

[6] LEUTE V, SCHMIDTKE H M. Thermodynamics and kinetics of the quasibinary system Hg_(3-3x)In_2xTe₃——Ⅰ. Investigations by X-ray diffraction and differential thermoanalysis [J]. J Phys Chem Solids, 1988, 49(4): 409-420.

[7] MAYNELL C A, SAUNDERS G A, SEDDON T. An order-disorder transformation in Hg₃In₂Te₆ [J]. Physics Letters A, 1970, 31A(6): 338-339.

[8] WANG Ling-hang, DONG Yang-chun, JIE Wan-qi. Growth and electrical properties of mercury indium telluride single crystals [J]. Materials Research Bulletin, 2007, 42(11): 1949-1954.

[9] WANG Ling-hang, DONG Yang-chun, JIE Wan-qi. Growth, structure and electrical properties of mercury indium telluride single crystals [J]. J Phys D: Applied Physics, 2007, 40: 3921-3924.

[10] WEITZE D, LEUTE V. The phase diagrams of the quasibinary systems HgTe/In₂Te₃ and CdTe/In₂Te₃ [J]. Journal of Alloys and Compounds, 1996, 236: 229-235.

[11] GRUSHKA G G, BAKHTINOV A G , GRUSHKA Z M. Advanced semiconductor compound Hg₃In₂Te₆ [J]. J Adv Materials, 1997, 4(1): 36-39.

[12] WANG Ling-hang, JIE Wan-qi. Single-crystal growth of mercury indium telluride (MIT) by Vertical Bridgman method [J]. J Cryst Growth, 2006, 290: 203-206.

[13] WANG Ling-hang, JIE Wan-qi, ZHA Gang-qiang, XU Gang. Growth and characterization of mercury indium telluride single crystals [J]. Materials Science and Engineering B, 2006, 133: 129-131.

[14] NYE J F. Physical properties of crystals [M]. Oxford: Clarendon, 1985: 93-164.

[15] CHEN Gang, LIAO Li-ji. The fundamental of crystal physics [M]. Beijing: Science Press, 2007: 110-150.

(Edited by CHEN Ai-hua)

Foundation item: Project(2007AA03Z442) supported by the National High-tech Research and Development Program of China; Project(20090451374) supported by China Postdoctoral Science Foundation

Corresponding author: Wang Ling-hang; Tel: +86-29-82668679; E-mail: uswlh@yahoo.com.cn