J. Cent. South Univ. Technol. (2010) 17: 554-559

DOI: 10.1007/s11771-010-0522-4                                                                        

Transition of super-hydrophobic states of droplet on rough surface

YE Xia(叶霞)^{1, 2}, ZHOU Ming(周明)¹, JIANG Da-lin(蒋大林)¹, LI Jian(李健)¹, CAI Lan(蔡兰)¹

1. Photonics Fabrication Science Center, Jiangsu University, Zhenjiang 212013, China;

2. School of Mechanical Engineering, Jiangsu Teachers University of Technology, Changzhou 213015, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: Twelve samples with periodic array square pillars microstructure were prepared on the silicon wafer by plasma etching techniques, on which space b of the square pillars increased from 5 to 60 μm. In order to study the effect of b on the wettability of the rough surface, the effects of apparent contact angle (CA) and sliding angle (α) of the droplet on the rough surface were measured with the contact angle meter. The results show that the experimental values of CA well agree with the classical wetting theory and α decreases with the increase of b. Two drop shapes exist on the samples’ surface, corresponding to the Cassie state and the Wenzel state respectively. The contact state in which a drop would settle depends typically on the size of b. On the role of gravitation, the irreversible transition of a drop from Cassie state to Wenzel state should occur at a certain space of the square pillars. Since the transition has implications on the application of super-hydrophobic rough surfaces, theoretically, the prediction of wetting state transition on square pillar array micro-structured surfaces provides an intuitionistic guidance for the design of steady super- hydrophobic surfaces.

Key words: square pillar microstructure; wetting mode transition; apparent contact angle; sliding angle

1 Introduction

Wettability is a very important property of solid surfaces for both fundamental research and practical applications. When the contact angle of a water drop on a clean solid surface is greater than 150?, the surface is considered to be super-hydrophobic. Super-hydrophobic surfaces play an important role in many applications, and may be used not only to resist water and fog condensation, but also to prevent contamination. So they have attracted great attention. It is well known that the roughness of a hydrophobic solid surface amplifies its hydrophobicity. The contact angle (CA) of water on the flat solid surfaces is typically of the order of 100?-120?, but reaches values as high as 160? to 175? if they are rough. This is frequently seen in nature [1-3] and has been demonstrated for micro-fabricated rough surfaces [4-9]. Two distinct hypotheses are classically proposed to explain this effect. One is that liquid wets the grooves of the rough surface and the roughness increases the surface area of the solid (Fig.1(a)), which geometrically enhances hydrophobicity (Wenzel state). The other is  that air can remain trapped underneath the drop inside the roughness grooves and the drop sits partially on air (Fig.1(b)), which leads to a super-hydrophobic behaviour (Cassie state). We shall refer to this as the composite contact with the rough substrate.

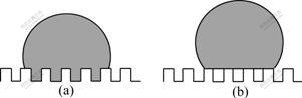
Fig.1 Drop on two rough surfaces: (a) Wenzel state; (b) Cassie state

The CA of the drop that wets the grooves is expressed by the following equation:

cos θ_W=rcos θ_Y                               (1)

where θ_Y is the intrinsic CA on a smooth surface, also known as Young’s contact angle, θ_W is apparent CA on a rough surface made of the same material, and r is the roughness factor, namely, the ratio of the actual area of a rough surface to the geometric projected area.

The CA of a drop that sits on the roughness peaks is given by Cassie’s equation:

cos θ_CB=-1+f(1+cos θ_Y)                        (2)

where θ_CB is the apparent CA assuming a composite surface, and f is an area fraction of solid in contact with the liquid.

MARMUR [10] pointed out that from the view of thermodynamics the wetting state which gave the minimum apparent contact angle is the most steady state, since here the Gibbs energy completely is translated into contact angle. Some researches indicated that Wenzel state applies to a middling hydrophobic surface while Cassie state applies to a high hydrophobic surface [11].

There is a threshold value θ_c between the two states (Fig.2). When 90?＜θ_Y＜θ_c, the droplets formed wetted surfaces (i.e., Wenzel state) are at lower energy, while  θ_Y＞θ_c, the droplets formed composite surfaces (i.e. Cassie state) are at lower energy. However, it has been reported that the Cassie state can be also observed for   θ_Y＜θ_c, in spite of a higher energy. In such a case, the droplets are at metastable state and the micro-structured surfaces are at middling hydrophobic state which is represented by a dashed line. This state is very unstable and in a certain condition (such as increasing volume of the droplets and bringing pressure to bear on the droplets) the irreversible transition to Wenzel state (intituled as C/W transition) which is with lower systematic energy would occur [12].

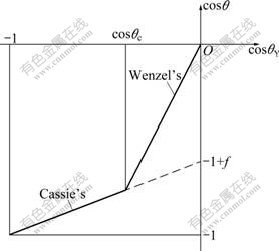
Fig.2 Prediction by Wenzel and Cassie formulas (when θ_Y＜θ_c, wetting contact gives lower energy, and when θ_Y＞θ_c, composite contact gives lower energy)

PATANKAR [13-14] did a lot of work about of C/W transition. They discussed the metastability of the super-hydrophobic states, and proposed the concept of energy barrier and the methodology to determine whether the C/W transition is possible from the view of energy equilibrium. They theoretically discussed the transition criteria between two wetting states. The up-to-date research of LI and AMIRFAZLI [15] also involved thermodynamically integrated analysis about influencing factors of  C/W transition, and firstly put forward the concept of critical height (h_c) and posed a general criterion for wetting state transition (i.e., h＞h_c) from the view of geometry. But they have not further studied calculation methods of the critical height for concrete shapes of surface micro-structures and not experimentally verified the transition.

In this work, we studied the effect of the parameters on the wettability of the square pillars micro-structure surfaces and aimed to confirm the C/W transition on such a surface with experimental method, and provided the theoretical guidance for the design of steady super- hydrophobic surfaces.

2 Theoretical background

Let the rough surface be made of periodically placed square pillars of size a×a, height h, and spacing b arranged in a regular array (Fig.3). In regard to the one period lined out by the dashed line frame in Fig.3, according to the definition of r and f, the apparent CAs of the drop on square pillar array microstructure surfaces in two states are theoretically predicted by Eqs.(3) and (4), respectively:

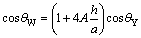                      (3)

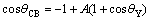                     (4)

where A=(a/(a+b))². They are also general applicable equations to express the relationship between geometric parameters of square pillar array microstructures and the apparent contact angles.

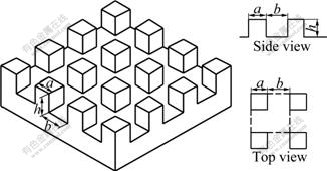
Fig.3 Sketch of square pillar array microstructures and their geometric parameters

Strictly speaking, super-hydrophobic surface should meet two conditions: the larger contact angle and the smaller sliding angle. Sliding angle is the critical angle that the droplet placed on tilted solid surface begins rolling.  In general, sliding angle is denoted by α [16] and used to character the hysteresis of the solid surface. The smaller the sliding angle, the more hydrophobic the solid surface.

3 Experimental

The fabrication of periodic array square pillars micro-structures was completed by plasma etching techniques. In our experiments, twelve samples were manufactured and numbered as 1-12. The microstructure of sample was observed and evaluated on a scanning electron microscope (SEM, JSM-840A, JEOL Ltd., Japan). The geometric parameters of micro-structure were as follows: the widths of square pillars a were all  6 μm, the heights of square pillars h were all 10 μm, and the spaces of the square pillars b gradually increased from 5 to 60 μm. The geometric parameters of micro- structure of all samples are shown in Table 1. Before testing the contact angle and sliding angle, the samples were cleaned by supersonic in deionized water for 30 min at room temperature. And then the surfaces of the samples were rinsed in turn by deionized water, acetone and anhydrous ethanol to remove any impurity and organic matter on them. After drying by cold air, the samples were exposed to trichloro(1H, 1H, 2H, 2H- perfluorooctyl)silane(CF₃(CF₂)₅CH₂CH₂SiCl₃) at 70 ℃ for 2 h in a vacuum oven. The solution was evaporated and coated on the samples’ surfaces to decrease the surface free energy.

The sessile drop method was used for apparent CA measurements with a contact angle meter (OCAH200, Dataphysics, Germany). The droplets used in testing were drops of deionized water with volumes of 1 μL and 6 μL, respectively. Contact angles were measured at five different points for each sample, and average values were calculated. The sliding angle (α) of drop on the rough surfaces was measured with water droplets of 6 μL and also measured five times to average. In each experiment, the droplet was placed on the horizontal sample surface firstly, and then the whole testing system was tilted and rotated, the whole process from the rotation to drop rolling was recorded, and the tilted angle of system was obtained as the sliding angle when the drop just rolled.

4 Results and discussion

Fig.4 shows the SEM image of periodic square pillar microstructures. A well-ordered array of pillars is observed on a silicon surface. The theoretical predictions of contact angle for the composite and wetted cases are all shown in Table 1. The experimental values of contact angles and sliding angles are also shown in Table 1.

Before testing, all samples were modified with trichlorosilane. It should be known that the experiment measured the apparent contact angle of the drop on the silane-treated silica-smooth surface to be 120.7?. The CA of silane-treated surface is increased by 70?-80? than that of the drop on the unmodified silica-smooth surface. This shows that the silica-smooth surface has achieved changes of wettibility from hydrophilic to hydrophobic.

4.1 Two states on sample surfaces

Fig.5 shows the photographs of a 1 μL water droplet on the prepared surfaces with square pillar micro- structures. On the surface of samples 1 to 8 (with pillar spaces b from 5 to 40 μm), we can see the similar images of the droplet sit on the peak of the roughness, as shown in Fig.5(a). It is clearly seen that the light can pass through the interspace between the droplets and the rough surface, which indicates that a composite surface is formed.

The measured apparent contact angle in Table 1 is closer to the value predicted by Cassie’s formula. In the testing process of samples 9 to 12 (with pillar spaces b from 45 to 60 μm), the droplet was very difficult to be adsorbed on the surface samples, rather firmly adhered to the needle with teflon coating. However, once the droplet adhered to the sample surface, the droplet fully would wet the depressions of the rough surface. The image of droplet in such a status is shown in Fig.5(b). Light cannot be seen between the droplet and the rough surface. Again, the measured apparent contact angle is indeed closer (seen in Table 1) to that predicted by Wenzel’s formula based on the hypothesis of a rough surface. This indicates that on the silicon-based square pillar array micro-structured surfaces, droplets display two contact states of Cassie contact (for samples 1-8) and Wenzel contact (for samples 9-12).

Table 1 Contact and sliding angle of twelve samples with different roughness parameters

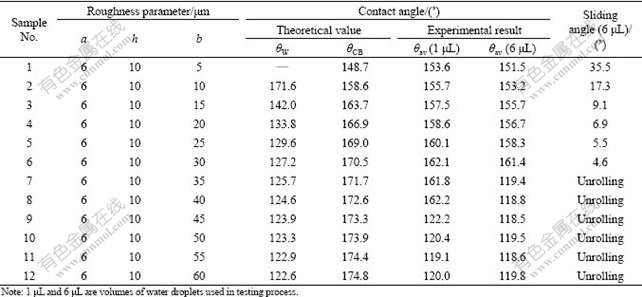
Fig.4 SEM image of periodic microstructures on silicon-based surface with square pillar array

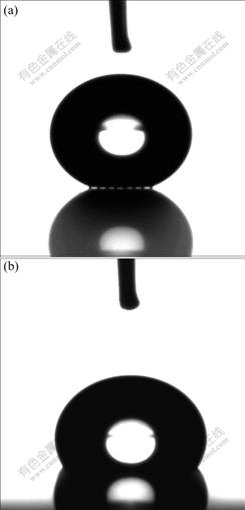
Fig.5 Images of droplet on samples’ surfaces: (a) In Cassie state; (b) In Wenzel state

4.2 Effect of spacing b on apparent contact angle

Based on the experimental results of the apparent contact angles of the drop on the surface of samples 1-8, the larger the space b, the greater the apparent contact angle. This result agrees with the prediction of the Cassie’s formula.

According to the theoretical formula, the area fraction of solid in contact with the liquid (f) decreases with the increase of space b between the pillars. And the apparent contact angle of water on the sample surface becomes larger. Namely, the super-hydrophobicity of the rough surface is enhanced. However, when b is added to a critical value, the apparent contact angle of the droplet becomes smaller suddenly (on the surface of sample 9), because at this time the wetting state is irreversibly transformed from Cassie state to Wenzel state. Fig.6 shows that the wettability of the sample surface changes between samples 8 and 9. But only from the view of thermodynamics, the transition should happen between samples 2 and 3 (at the critical point in Fig.6). The reasonable interpretation is that there are energy barriers between two states [13]. To make C/W transition, it is necessary to overcome the energy barrier. When the space between the pillars increases, the center of mass of the Cassie drops lowers. The gravitational potential energy of the whole system reduces. According to the quantitative conservation of energy, the reduction of the potential energy can be used to overcome the energy barrier, which eventually leads to the occurrence of C/W transition of droplets on the sample surface.

Fig.6 Contrastive curves of apparent contact angle values between experimental results and theoretical predictions θ_W as well as θ_CB for surfaces of samples

Some similar cases are observed on the droplets with a volume of 6 μL which are settled on the rough surfaces. The difference is that the transition of two states took place between samples 6 and 7 (as shown in Table 1 and Fig.6) instead of between samples 8 and 9. This is because the bigger the droplet size, the larger the gravity. When the space of the pillars is added with the same value, the reduction of gravitational potential energy of larger droplet is more than that of smaller droplet. And in this instance the energy barrier is easier to be overcome on the same rough surface. Even if gravity plays an insignificant role in determining the drop shape, it can play an important role in the C/W transition. This is further evidence of that there should be the energy barrier between Cassie state and Wenzel state, and this barrier should be overcome to achieve the C/W transition. Our experiments confirm that the wetting state of the solid surface can be transformed by changing geometric parameters of the micro-structure. This fact is significant in microfluidic application, where a rough surface is used for applications based on wettability amplification. If the apparent contact angle changes as a result of a transition, it can result in different surface characteristics. To avoid an evident contact angle change due to external disturbance, the appropriate geometric parameters of the micro-structure surface should be designed to assure that droplets on the rough surface should be as far as possible to remain in a stable Cassie state (superhydrophobic area) and not prone to C/W transition.

4.3 Effect of geometric parameter b on sliding angle

In the experimental process of testing sliding angle, we found that the volume of droplet has great influence on the test results. On the same sample surface (with the same hydrophobicity), the larger the droplet size, the smaller the sliding angle. From another point of view, the wettability of the rough solid surface is influenced by the gravitational potential energy. Limited by the sample size and injection system, the droplet size could not be too large. Therefore, the droplet with the volume of 6 μL was used to test the sliding angle. In the experiment, it was observed that all Cassie droplets could roll down, even though the area of the droplet contacting with the sample surface varied obviously between different samples. The Wenzel droplets never rolled even if the testing system was tilted with angle of 90?. This indicates that the contact state influences the rolling of the droplet remarkably. The experimental results of sliding angle are shown in Table 1. And Fig.7 shows a sketch of the measurements of sliding angle as a function of the geometric parameter b. This shows that when the width a and height h of the pillars do not change, the sliding angle gradually decreases with the increase of the space b of the pillars. In other words, the super-hydrophobicity of the rough surface enhances with the increase of b. However, when b is added to a certain extent, the drop sticks to the sample surface for hysteresis, no longer rolling. This is because the contact states of droplets are transformed from Cassie state to Wenzel state at this time. This agrees with the experimental results of the contact angle.

It is worth noting that sliding angles in Table 1 are all greater than 2?, which is restricted by the testing method. In our experiments, the droplet was dripped on the horizontal sample surfaces. After reaching equilibrium, the testing system was tilted to measure the sliding angle. It is clear that compared to the method of tilting the testing system firstly, and then dripping the droplet, the adherence of the droplet on the surface is greatly enhanced because of the affects of gravitation. Therefore, the droplet rolls with more difficult owning to the role of the surface tension. Using the latter method, the testing value of the sliding angle of the droplet on the surface of sample 6 is 1?-2?.

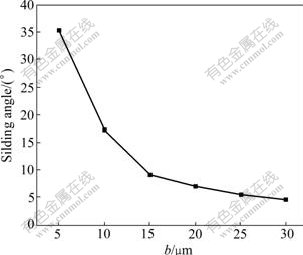
Fig.7 Relationship of α as function of geometric parameter b

5 Conclusions

(1) Based on the classical wetting theories we took the three-dimensional square pillar array micro- structured surfaces as a study object and theoretically predicted the apparent contact angles on such surfaces. Also we designed and fabricated square pillar array samples through plasma etching technology on the silicon wafer surface and carried out some experimental tests and analysis on wettability as well as super- hydrophobic stability.

(2) There could be two wetting states corresponding to Cassie’s and Wenzel’s theory on the same micro-structure surface, and under certain conditions the irreversible C/W transition would occur. The effects of wetting mode transition must be considered when we design and fabricate micro-structured surfaces.

(3) The wettability of the rough surface depends on the geometric parameters of the micro-structure of the surface. On the square pillar array micro-structured surfaces, in a certain range, when the width and height of the square pillars do not change, the larger the space of the square pillars, the higher hydrophobic the surface. But when the space is added to certain extend, the wetting state irreversibly transforms from Cassie state to Wenzel state. At this moment, the gravity plays an important role. And the test results of rolling angle are also consistent with this result.

(4) The theoretical predictions match experiments. So from the view of geometry, the wetting state transition on square pillar micro-structured surfaces can be theoretically predicted, which will provide a direct guidance for the design of steady super-hydrophobic surfaces.

(5) In later researches, the effect of the width and height of the square pillars on the hydrophobility of the rough surface should be further experimentally investigated. The energy-based theoretic criteria for wetting state transition will be deduced and the wetting state transition of other various regular geometric microstructure surfaces will be examined.

References

[1] BARTHLOTT W, NEINHUIS C. Purity of the sacred lotus, or escape from contamination in biological surfaces [J]. Planta, 1997, 202: 1-8.

[2] GUO Zhi-guang, LIU Wei-min. Biomimic from the super- hydrophobic plant leaves in nature: Binary structure and unitary structure [J]. Plant Science, 2007, 172: 1103-1112.

[3] NEINHUIS C, BARTHLOTT W. Characterization and distribution of water-repellent, self-cleaning plant surfaces [J]. Annals of Botany, 1997, 79: 667-677.

[4] LIN Feng, LEI Jiang. Preparation and investigation of super-hydrophobic nanoscale interfacial materials [J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2005, 22(1): 106-109.

[5] CALLIES M, CHEN Y, MARTY F, PEPIN A, QUERE D. Microfabricated textured surfaces for super-hydrophobicity investigations [J]. Microelectronic Engineering, 2005, 78/79: 100-105.

[6] YOSHIMITSU Z, NAKAJIMA A, WATANABE T, HASHIMOTO K. Effects of surface structure on the hydrophobicity and sliding behavior of water droplets [J]. Langmuir, 2002, 18(15): 5818-5822.

[7] BICO J, MARZOLIN C, QU?R? D. Pearl drops [J]. Europhys Lett, 1999, 47: 220-226.

[8] ?NER D, MCCARTHY T J. Ultrahydrophobic surfaces. Effects of topography length scales on wettability [J]. Langmuir, 2000, 16(20): 7777-7782.

[9] BALDACCHINI T, CAREY J E, ZHOU M, MAZUR E. Superhydrophobic surfaces prepared by microstructuring of silicon using a femtosecond laser [J]. Langmuir, 2006, 22(11): 4917-4919.

[10] MARMUR A. Wetting on hydrophobic rough surfaces: To be heterogeneous or not to be? [J]. Langmuir, 2003, 19(20): 8343-8348.

[11] LI W, AMIRFAZLI A. A thermodynamic approach for determining the contact angle hysteresis for superhydrophobic surfaces [J]. J Colloid Surface Sci, 2005, 292: 195-201.

[12] HE B, PATANKAR N A, LEE J. Multiple equilibrium droplet shapes and design: Criterion for rough hydrophobic surfaces [J]. Langmuir, 2003, 19(12): 4999-5003.

[13] PATANKAR N A. Transition between superhydrophobic states on rough surfaces [J]. Langmuir, 2004, 20(17): 7097-7102.

[14] PATANKAR N A. On the modeling of hydrophobic contact angels on rough surfaces [J]. Langmuir, 2003, 19(4): 1249-1253.

[15] LI W, AMIRFAZLI A. Microtextured superhydrophobic surfaces: A thermodynamic analysis [J]. Advances in Colloid and Interface Science, 2007, 132(2): 51-68.

[16] KIJLSTRA J, REIHS K, KLAMT A. Roughness and topology of ultra: Hydrophobic surfaces [J]. Colloids Surface

Foundation item: Project(50435030) supported by the National Natural Science foundation of China; Project supported by the Program for New Century Excellent Talents in Chinese University; Project(GZ080010) supported by the Open Research Fund Program of Jiangsu Province Key Laboratory for Photon Manufacturing Science and Technology

Received date: 2009-05-17; Accepted date: 2009-10-26

Corresponding author: ZHOU Ming, Professor; Tel: +86-511-88791458; Fax: +86-511-88791288; E-mail: zm_laser@126.comScience, 2002, 206: 521-529.

(Edited by YANG You-ping)