J. Cent. South Univ. (2012) 19: 55-62

DOI: 10.1007/s11771-012-0972-y

Simulation of pressure effects on

hot isostatic pressing of stainless steel powder

LIU Guo-cheng(刘国承), SHI Yu-sheng(史玉升), WEI Qing-song(魏青松), XUE Peng-ju(薛鹏举)

State Key Laboratory of Materials Processing and Die & Mould Technology,

 Huazhong University of Science and Technology, Wuhan 430074, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: To investigate the effects of pressure on the hot isostatic pressing (HIP) process of a stainless steel powder, density distribution and deformation of the powder at four different applied pressure levels were predicted and compared by using finite element method (FEM). Constitutive relations of porous compacts during HIP process were derived based on the yield criterion of porous metal materials. Thermo-mechanical coupling calculations were carried out by the MSC.Marc. Densification mechanisms were studied through evolutions of relative density, equivalent plastic strain and equivalent viscoplastic strain rate for compacts. The simulation results were also compared with experimental data. The results show that the densification rate and final density of compacts increase dramatically with the increase in the applied pressure level when it is below 100 MPa during HIP process, and the creep for compacts evolves into steady stage with the improvement of density.

Key words: hot isostatic pressing (HIP); stainless steel powder; numerical simulation; densification mechanism; applied pressure

1 Introduction

Hot isostatic pressing (HIP) is a powder metallurgy (PM) technique for consolidating powders to full density. The HIP process is commonly used to manufacture homogeneous compacts with precise tolerances which is the major driving force for its commercial development [1]. Pressure and temperature as the key technical parameters are transmitted to the powder through its container. A typical HIP cycle consists of three stages: elevating pressure and temperature to peaks, then holding them for some time, and finally decreasing them to normal states. The highest holding temperature is usually greater than 0.7 times melting point [2]. High temperature maybe induces the grain growth, accordingly decreasing the mechanical properties.

Numerical simulations provide some effective methods to investigate the densification and deformation behaviors of powder compacts during the HIP process. Two different types of mathematical models have been used to simulate the HIP process. A microscopic approach is based on the local behavior of particles sintered. HELLE et al [3] established the HIP maps using densification rate equations to show predominant mechanisms for the HIP densification. However, the microscopic approach is difficult to predict the shape changes of compacts [4]. A macroscopic method is established based on the theories of continuum mechanics. Many constitutive equations based on the power-law creep equations have been proposed to predict the flow behavior of powders during HIP process [5-6]. ARYANPOUR [7] also presented a new elasto-plastic- viscoplastic model for HIP of metal powders considering over-consolidation conditions for powders. Many researchers also worked on the deformation of container during the HIP process and optimized its design through the macroscopic method [8-10]. All these simulation investigations mentioned above mainly concentrated either on developing constitutive models in order to understand the powder densification mechanisms or on forming the complex components with near-net shape during the HIP process.

However, the applied pressure, which is one of the most important factors during the HIP process, significantly influences not only final configurations but also densification behavior of compacts [11-12]. The powdered metals under high temperatures and pressures exhibit simultaneously the phenomena of creep and plasticity. The PERZYNA viscoplastic rheological model [13] can provide a unified approach to them. Therefore, the major objective of this study is to investigate the pressure effects on the AISI 316L powder during the HIP process by using finite element method (FEM) according to a modified PERZYNA model, and the simulation results were also compared with experimental data.

2 Finite element analysis

2.1 Physical model

The HIP process for powders is a thermo- mechanical coupling progress. Large thermal gradient will cause thermal strain to compacts. The thermal viscoplastic structure for the constitutive relationship of the powder compacts underlying classical viscoplasticity is motivated by examining the response of the mechanical device arranged, as illustrated in Fig. 1. The device consists of a thermal element with a coefficient of thermal expansion α for powder materials connecting to the combination elements, which has a dashpot of a viscosity coefficient η in parallel with a coulombic frictional device with the yield stress of powder compacts σ_y. The viscoplasticity is composed of a dashpot and a friction element and mainly characterizes viscoplastic deformation in creep.

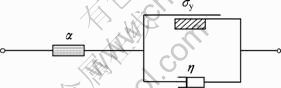
Fig. 1 Thermal viscoplastic model for HIP process of powder compacts

When stress is applied to the device, the total strain rate 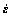 in the thermal viscoplastic simulation for powders during the HIP process can be given by

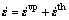
where 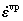 is the viscoplastic strain rate;  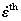is the thermal strain rate. The viscoplastic strain rate can be expressed by many formulations, such as power-law creep equation. In this study, the viscoplastic strain rate is defined in the PERZYNA model [13-14] as

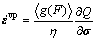
where g is monotone and Q means the plastic potential. The symbols á·? is defined as follows

The thermal strain rate can be defined as

where 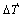 is the temperature variable rate in a time interval; m=[1, 1, 1, 0, 0, 0]^T. During a time interval, thermal strain tensor increments and viscoplastic strain tensor increments can be got from some numerical integration calculations. The nonlinear equations can be solved by a modified Newton-Raphson algorithm.

2.2 Constitutive equations

At the beginning of the HIP process, porous compacts are highly compressible. From a macroscopic point of view, compacts can be considered as porous parts with the relative density ρ defined as

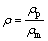
where ρ_p is the density of porous materials and ρ_m represents the theoretical density of matrix materials.

One general form of the equivalent stress σ_eq for porous materials used by many investigators [5, 15] is defined as

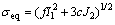
where I₁=tr(σ), J₂=1/2S:S, S=σ-σ_mI and σ_m=1/3tr(σ). Here, σ is the Cauchy stress tensor; S means the deviatoric stress tensor; σ_m is the mean stress; I is the second-order unitary tensor; tr(·) denotes the trace operator; I₁ and J₂ represent the first invariant of stress tensor and the second invariant of deviatoric stress tensor, respectively; f and c are functions of relative density which can be experimentally determined.

The loading function F for porous materials with isotropic hardening can be written as

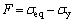
where σ_y is the yield stress of the porous materials depending on the yield stress of the matrix materials and relative density. F<0 means that any deformation process on the materials is elastic. F=0 represents that the porous materials occur plastic deformation. Substituting Eq. into Eq. , we can get the yield surface, which forms an elliptical volume in principal stress space with major axis coincident with the hydrostatic axis. This yield criterion is an extension of the Von-Mises criterion to porosity [16].

When an associative viscoplastic flow rule with g(F)≡F is considered, the flow function is directly equivalent to plastic potential, and Eq. can be written as

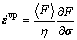
Equation is the associative version of the flow rule and isotropic hardening law for viscoplasticity. Then, we can get the PERZYNA type viscoplasticity based on elliptical yield function for porous materials [17]. Substituting Eqs. - into Eq. gives

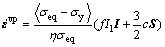
The main feature of Eq. is the overstress used for describing the viscoplasticity. As shown in Eq. , there is viscoplastic strain while the equivalent stress is over the yield stress. Then, Eq. can present the creep and plastic deformation for powder materials.

The mechanical behavior of the container materials during the HIP process can be considered to be elasto-plastic and governed by the Von-Mises yield criterion, i.e.,

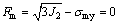
where F_m and σ_my are loading function and yield stress of container materials, respectively. The containers are also assumed to obey the associated flow rule and require a thermo-mechanical coupling analysis because of high temperature effect.

The strain increment dε of containers can be got as follows:

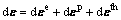
where dε^e, dε^p and dε^th are elastic strain tensor increments, plastic strain tensor increments and thermal strain tensor increments, respectively.

The plastic strain tensor increment is expressed as

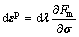
where dλ is the plastic proportional scalar, depending upon the material yield strength, the current state of stress and the strain increments, varying throughout the deformation history. During a time interval dt_n=t_n+1-t_n, the thermal conduction is described by Fourier's law.

The temperature increment is dT, and then the thermal strain tensor increment is rewritten as

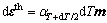
where α_T+dT/2 is the average thermal expansion at a time interval.

From Hooke's law, the stress tensor increment is calculated as

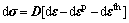
where D is the stiffness tensor. During the decoupling process, a change in the temperature distribution contributes to the deformation of powder and container configurations through thermal strains and influences the material properties, but deformation converting mechanical work into heat is ignored in this work.

3 FEM simulation

3.1 Mesh and material properties

The height of a cylindrical specimen was 100 mm, the inner diameter was 40 mm and the thickness was   2 mm. The first quadrant of section for the sample was considered due to axisymmetry in the z axis and symmetry in the r axis. The finite element mesh is shown in Fig. 2. The powder material was the AISI 316L stainless steel and the container material was the AISI 304 stainless steel. The eight-noded isoparametric distorted quadrilateral elements with biquadratic interpolation and full integration were used in the thermo-mechanical coupling analysis. The powder and container configurations consisted of 392 and 108 elements, respectively. The nodes at left and bottom boundaries of this mesh were fixed with the r and z axes, respectively. Temperature and pressure loads were applied to the outer boundaries of the container.

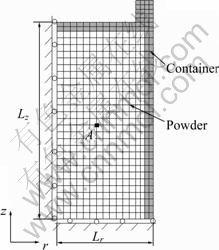
Fig. 2 Finite element mesh and boundary conditions for AISI 316L stainless steel powder and AISI 304 container configurations

As shown in Eq. , the equivalent stress of AISI 316L stainless steel powder is determined by the parameters of f and c. These parameters were derived from uniaxial creep tests under high temperature for samples with different levels of relative density obtained from the interrupting HIP experiments [18] as

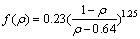
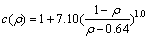
Some material properties of porous metals could be got from full density by empirical relationships. Thus, the elastic modulus E, Poisson ratio ν and viscosity coefficient η are given by the following functions [7, 19-20], respectively:

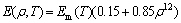
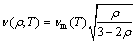
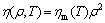
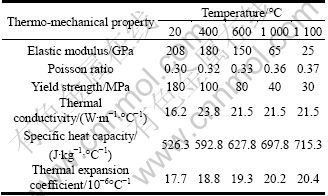
where E_m(T), ν_m(T) and η_m(T) are temperature-dependent elastic modulus, Poisson ratio and viscosity coefficient of matrix material, respectively. Other relevant thermo- mechanical properties for AISI 316L stainless steel powder can be obtained from literature or directly measured in the tests of porous samples. Table 1 gives the effects of temperature on the mechanical and thermal properties of AISI 304 stainless steel [6, 21].

Table 1 Temperature dependent thermo-mechanical properties of AISI 304 stainless steel

3.2 Loading conditions and numerical solutions

As shown in Fig. 3, four HIP schedules were designed. The temperature cycle was held for 2 h at    1 030 °C. Different holding pressure levels of 60, 80, 100 and 120 MPa were employed. Each HIP schedule had same temperature cycle but different pressure cycles. The initial relative density of the powder was assumed to be 0.67. The incremental solution scheme with a fixed load stepping scheme was chosen and all the operations were implemented with the commercial program of MSC.Marc.

Fig. 3 Schedules for pressures and temperature during HIP cycles

4 Results and discussion

4.1 Relations between pressure loads and relative densities

Figure 4 shows the simulation results of the relative density distribution and deformed configurations after the HIP process with different pressure cycles (Fig. 3). The original outlines of container configuration were also plotted in order to study the container deformation. The relative density distributions in the powder configurations were non-uniform despite the uniform external loads were applied to containers during the HIP process. The relative density in the corner region of powder configurations (near point B) was the lowest. This phenomenon also agrees well with the experimental data [22]. Temperature gradients causing densification waves can lead to anisotropic shrinkage in the powder configurations [23]. It can be clearly indicated that compacts are more homogeneous with the increase in holding pressure loads. The average relative density increased sharply from 0.81 to 0.95 when the holding pressure loads rose from 60 MPa to 100 MPa, as shown in Fig. 4. However, the increasing speed of the average relative density was reduced greatly when the pressure exceeded 100 MPa. This phenomenon may be attributed to the lower deformation resistance at low relative densities (typical ρ<0.9) [2]. In this case, particles are discrete and touchable at sintering necks. The relative density can be improved significantly by increasing the pressure. Deformation resistance increases dramatically when compacts achieve high density with massive isolated pores. The densification mechanisms are governed by plastic and creep deformation [22].

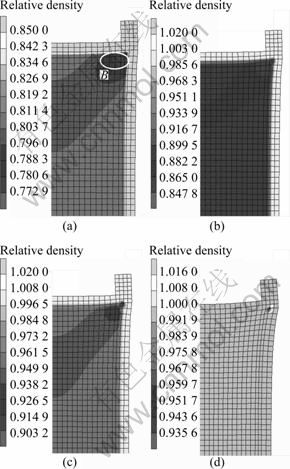
Fig. 4 Relative density distributions of AISI 316L powder and container after HIP cycles with different holding pressures: (a) 60 MPa; (b) 80 MPa; (c) 100 MPa; (d) 120 MPa

4.2 Relations between pressure loads and densification procedures

The curves in Figs. 5(a)-(c) respectively illustrate the evolution of the relative density, equivalent plastic strain and equivalent viscoplastic strain rate at node A shown in Fig. 2 during different HIP cycles with the various holding pressure loads. At the early elevating stage of the HIP cycles, relative density decreased clearly, meanwhile the equivalent plastic strain and equivalent viscoplastic strain rate nearly maintained zero. The reasons for these results are that the thermal expansions of compacts and containers play an important role at this time, and the applied pressure transferred to the powder configurations gets weakened because of the significant shielding effects of containers [22, 24]. Low applied pressure is difficult to cause particles deformation. Viscoplastic deformation of powder compacts has not occurred at this moment. With the increase in pressure and temperature at the later elevating stage, it was clearly seen that there were sharp increases in the equivalent viscoplastic strain rate and equivalent plastic strain. Correspondingly, the densification rate had a great improvement. Most of the densification behaviors took place during this period for the curve of “120 MPa HIP” in Fig. 5(a). The densification rate had a dramatic improvement by increasing the applied pressure. This can be attributed to not only the pressure causing flow on particles but also the movements of particles and porosity elimination.

When the applied pressure evolved from an elevating stage into holding stage, the maximum equivalent viscoplastic strain rate was achieved since the applied pressure reached its peak. Correspondingly, the crest value of equivalent viscoplastic strain rate increased when increasing the pressure level. The equivalent plastic strain and relative density increased gradually in the holding stage; meanwhile, the equivalent viscoplastic strain rate decreased quickly due to work hardening, and performed the typical characteristics of a transient creep stage. The mechanisms of densification in this stage are attributed to the following actions: viscoplastic deformation, particles rearrangements, collapse of isolated pores and particle relative motions which involve relative translations and rigid body rotations. The coordination number or the number of contacts per particle also increases noticeably [22]. Then, creep mechanisms (involving power-law creep, diffusion creep and so on) get to be the dominant roles of densification and deformation behaviors during this stage [25-26]. Consequently, the equivalent viscoplastic strain rate tends to be a constant (between A and B as displayed in Fig. 5(c)) due to the balance between work hardening and thermal softening of compacts, and equivalent plastic strain presents linear growth as the curve of “120 MPa HIP” shown in Fig. 5(b). With the development of creep, the improvement of relative density is attributed to the increment of equivalent plastic strain and elimination of pores. The creep gradually progresses to a steady stage from the transient creep stage.

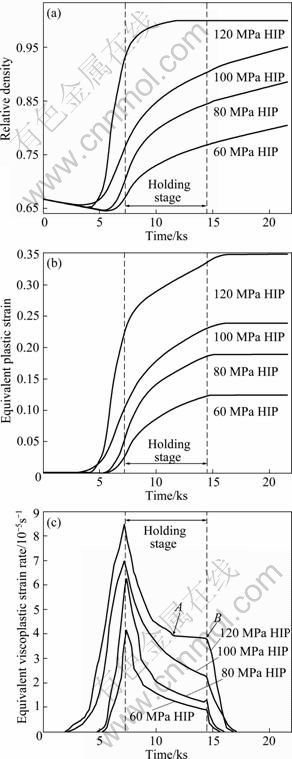
Fig. 5 Evolution of various variables at node A during various HIP cycles with different holding pressures: (a) Relative density; (b) Equivalent plastic strain; (c) Equivalent viscoplastic strain rate

During the descent stage, there was a sharp decrease of the equivalent viscoplastic strain rate. The relative density of compacts also had a little improvement although there was no increase of the equivalent plastic strain. This phenomenon is mainly caused by the cooling shrinkage of compacts and containers. It is quite evident that the most densification behavior occurs at the elevating and holding stages.

5 Verification

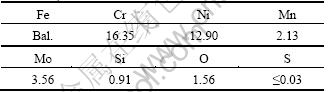
In order to compare the numerical results with experimental data, two HIP cycles were studied. The materials and dimensions of samples have also been described above. In this wrok, a gas atomised spherical stainless steel powder (AISI 316L) with an average particle size of 16 μm, melting point range between 1 375 °C and 1 400 °C, and theoretical density of 7.95 g/cm³ was used. The chemical compositions of the stainless steel powder are given in Table 2.

Table 2 Chemical compositions of stainless steel powder (mass fraction, %)

A scanning electron microscopy (SEM) micrograph of the gas atomised stainless steel powder is depicted in Fig. 6. Tap density of samples was achieved on vibration platform. As displayed in Fig. 3, two HIP schedules are studied. Case 1 is under 60 MPa at 1 030 °C and Case 2 is under 100 MPa at 1 030 °C.

Fig. 6 SEM micrograph of gas atomised AISI 316L stainless steel powder

The cross-sectional samples are shown in Fig. 7. The trends of deformation are very similar with the simulation results.

Fig. 7 Deformed profiles of powder compacts after HIP process at 1 030 °C: (a) 60 MPa; (b) 100 MPa

The initial dimension, the simulation, and the experimental dimensions after the HIP process are denoted by D_ini, D_sim and D_exp, respectively. The relative error is defined as follows:

where E_rel is the relative error between the simulation and experimental dimensions. As shown in Fig. 2, two key geometrical parameters were studied. The results are calculated and given in Table 3. It is apparent that the precision in the radial direction is better than that in the axial direction and the maximum relative error is about 7.0%. This may be due to the effect of weld at plugs.

Average relative density, 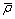, was measured by the Archimedes method. After the HIP process,  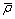is 0.90 for Case 1 and 0.97 for Case 2. Correspondingly, it is about 0.09 and 0.02 higher than simulation results, respectively.

Table 3 Dimensions and simulation errors for tow cases

The SEM micrographs of the powder compacts are illustrated in Fig. 8. From Fig. 8(a), it is quite evident that lots of pores are still remained in the compact. With the increase in the holding pressure, it is helpful to eliminate pores and therefore improve the density of the compacts. The results reveal that simulation results have a slight underestimation, but the error is low. Therefore, these simulation results are reliable.

Fig. 8 SEM micrographs of powder compacts after HIP process at 1 030 °C: (a) 60 MPa; (b) 100 MPa

6 Conclusions

1) When the applied pressure is less than 100 MPa, the average relative density and homogeneity of powder compacts have a great improvement with the increase in the applied pressure during the HIP process. The equivalent viscoplastic strain rate and equivalent plastic strain of powder compacts also rise quickly. It is also helpful to improve the viscoplastic deformation for particles by increasing the applied pressure.

2) The equivalent viscoplastic strain rate of powder compacts reaches its crest value once the applied pressure elevates to the peak. Transient creep plays a critical role in densification progress. Creep of powder compacts evolves into a steady stage from the transient stage with the improvement of relative density during the holding stage.

3) Finite element calculations agree well with experimental results. The FEM provides an effective approach to study the densification behavior of powders during the HIP process. It is helpful to obtain complicated HIP products with near net shape.

Acknowledgements

The authors are sincerely grateful to School of Materials Science and Engineering of Southwest Jiaotong University. We would like to give thanks to Analyzing and Testing Center of Huazhong University of Science and Technology for providing the apparatus to perform microanalysis and performance measurements in this work.

References

[1] BOCANEGRA-BERNAL M H. Hot isostatic pressing (HIP) technology and its applications to metals and ceramics [J]. Journal of Materials Science, 2004, 39(21): 6399-6420.

[2] ATKINSON H V, DAVIES S. Fundamental aspects of hot isostatic pressing: An overview [J]. Metallurgical and Materials Transactions A-Physical Metallurgy and Materials Science, 2000, 31(12): 2981-3000.

[3] HELLE A S, EASTERLING K E, ASHBY M F. Hot-isostatic pressing diagrams: New developments [J]. Acta Metallurgica, 1985, 33(12): 2163-2174.

[4] LI W B, HAGGBLAD H A. Constitutive laws for hot isostatic pressing of powder compact [J]. Powder Metallurgy, 1997, 40(4): 279-281.

[5] ABOUAF M, CHENOT J L, RAISSON G, BAUDUIN P. Finite element simulation of hot isostatic pressing of metal powders [J]. International Journal for Numerical Methods in Engineering, 1988, 25(1): 191-212.

[6] SVOBODA A, HAGGBLAD H A, NASSTROM M. Simulation of hot isostatic pressing of metal powder components to near net shape [J]. Engineering Computations, 1996, 13(5): 13-37.

[7] ARYANPOUR G. Constitutive modeling for hot isostatic pressing of metal powders [J]. Journal of Porous Media, 2006, 9(1): 15-34.

[8] CHUNG S H, PARK H, JEON K D, KIM K T, HWANG S M. An optimal container design for metal powder under hot isostatic pressing [J]. Journal of Engineering Materials and Technology-Transactions of the ASME, 2001, 123(2): 234-239.

[9] YUAN W X, MEI J, SAMAROV V, SELIVERSTOV D, WU X. Computer modelling and tooling design for near net shaped components using hot isostatic pressing [J]. Journal of Materials Processing Technology, 2007, 182(1/2/3): 39-49.

[10] TERAOKU T. Hot isostatic pressing simulation for titanium alloys [J]. International Journal of Powder Metallurgy, 2008, 44(5): 57-61.

[11] HUANG Bai-yun, ZHOU Ke-chao, ZHENG Qing. Effects of HIPing pressure on microstructures and properties of TiAl alloy [J]. Journal of Central South University of Technology, 2000, 7(3): 140-142.

[12] KIM K T, YANG H C. Densification behaviour of titanium alloy powder under hot isostatic pressing [J]. Powder Metallurgy, 2001, 44(1): 41-47.

[13] PERZYNA P. Fundamental problems in viscoplasticity [J]. Advances in Applied Mechanics, 1966, 9(2): 244-368.

[14] SIMO J C, HUGHES T J R. Computational inelasticity [M]. New York: Springer-Verlag, 1998: 57-70.

[15] GREEN R J. A plasticity theory for porous solids [J]. International Journal of Mechanical Sciences, 1972, 14(4): 215-224.

[16] SHIMA S, OYANE M. Plasticity theory for porous metals [J]. International Journal of Mechanical Sciences, 1976, 18(6): 285-291.

[17] LIU G C, SHI Y S, WEI Q S, WANG J W, LI M. Thermal elasto-viscoplastic analysis based on Perzyna model for hot isostatic pressing of stainless steel powder [J]. Materials Research Innovations, 2011, 15(s1): s299-s302.

[18] SANCHEZ L, OUEDRAOGO E, FEDERZONI L, STUTZ P. New viscoplastic model to simulate hot isostatic pressing [J]. Powder Metallurgy, 2002, 45(4): 329-334.

[19] GASIK M, ZHANG B S. A constitutive model and FE simulation for the sintering process of powder compacts [J]. Computational Materials Science, 2000, 18(1): 93-101.

[20] OLEVSKY E, DUDEK H J, KAYSSER W A. HIPing conditions for processing of metal matrix composites using the continuum theory for sintering-I. Theoretical analysis [J]. Acta Materialia, 1996, 44(2): 707-713.

[21] JEON Y C, KIM K T. Near-net-shape forming of 316L stainless steel powder under hot isostatic pressing [J]. International Journal of Mechanical Sciences, 1999, 41(7): 815-830.

[22] DELO D P, PIEHLER H R. Early stage consolidation mechanisms during hot isostatic pressing of Ti-6Al-4V powder compacts [J]. Acta Materialia, 1999, 47(9): 2841-2852.

[23] LI W B, EASTERLING K E. Cause and effect of non-uniform densification during hot isostatic pressing [J]. Powder metallurgy, 1992, 35(1): 47-52.

[24] XU J, MCMEEKING R M. An analysis of the can effect in an isostatic pressing of copper powder [J]. International Journal of Mechanical Sciences, 1992, 34(2): 167-174.

[25] LI W B, ASHBY M F, EASTERLING K E. On densification and shape change during hot isostatic pressing[J]. Acta Metallurgica, 1987, 35(12): 2831-2842.

[26] KIM H S. Densification mechanisms during hot isostatic pressing of stainless steel powder compacts [J]. Journal of Materials Processing Technology, 2002, 123(2): 319-322.

(Edited by YANG Bing)

Foundation item: Project(2007AA03Z115) supported by the National High Technology Research and Development Program of China; Project (2009ZX04005-041-03) supported by the National Science and Technology Major Program of China; Project(2010MS046) supported by the Independent Fund of Huazhong University of Science and Technology, China

Received date: 2010-12-08; Accepted date: 2011-05-25

Corresponding author: WEI Qing-song, Associate Professor; Tel: +86-27-87558155; E-mail: hust_lgc@163.com