基于改进免疫遗传算法的机械零件的结构优化
张干清1,龚宪生1, 2
(1. 重庆大学 机械传动国家重点实验室,重庆,400044;
2. 重庆大学 机械工程学院,重庆,400044)
摘要:鉴于现有免疫遗传算法其收敛差的问题,剖析其理论体系本身存在的6大弊端,提出6条全新的免疫策略,以加快算法的收敛速度并提高其收敛精度。同时,对实码抗体与变量向量之间的关系进行阐述,将复杂的算法机理用图形直观地描述出来,以便于对免疫遗传算法的理解与实际操作;将可靠性分析的随机摄动法与其灵敏度分析相结合,对随机参数的概率分布为任意形状的机械零件计算其可靠度及其灵敏度的函数表达式,并创建可靠度对设计变量的灵敏度最低与体积最小的两目标数学模型;提出实现目标函数值之间保持动态平衡的全新模型,以实现上述两目标函数与像集法的对接;最后,以盾构机三级行星减速器轴为例,按照上述思想建立数学模型,编写改进的免疫遗传算法的MATLAB程序对其进行优化。研究结果表明:该算法的鲁棒性使行星减速器轴的总体积减小13.65%,与改进前相比,所提出的免疫遗传算法具有更快的收敛速度与更高的收敛精度。
关键词:免疫遗传算法;可靠性设计;灵敏度分析;结构优化
中图分类号:TH16 文献标志码:A 文章编号:1672-7207(2011)11-3359-11
Structural optimization for mechanical elements by modified immune genetic algorithm
ZHANG Gan-qing1, GONG Xian-sheng1, 2
(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;
2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China)
Abstract: In view of the low convergence of the current immune genetic algorithm (IGA), 6 inherent drawbacks were found existing in the current rationale of IGA. For these reasons, 6 new immune strategies which were corresponded to above drawbacks were put forward to accelerate the convergence speed and precision. The relationship between real-coded antibodies and variables vector was also presented, and the complicated algorithm mechanism was intuitively described by graphic, which made people understood easily and practically operate on IGA. The stochastic perturbation method of the reliability was combined with its sensitivity analysis to deduce their function formulas on mechanical parts whose probability distributions of random parameters were of arbitrary shape. The two-objective mathematical models were created to minimize the sensitivity of reliability with respect to designing variables and the volume. A new model was creatively proposed that could realize the dynamic balance between objectives, by which the objectives were smoothly combined with the image set method. Finally, the shafts of 3 stages planetary gear in shield tunneling machine were optimized as an example by means of the MATLAB programs languages that applied the modified IGA after their mathematical models were constructed according to the ideas above. The results show that the robustness of the improved IGA not only decreases the total volume of shaft of planet reducer by 13.65%, but also its velocity and accuracy of convergence are superior to that of the unimproved IGA.
Key words: immune genetic algorithm; reliability design; sensitivity analysis; structure optimization
对于高负荷作业的机械零件如盾构机行星减速器的轴,其结构的优化务必满足可靠性与稳健性的双重要求,以确保设计出的产品既安全又经济[1-2],为此,必须提供一种可以提高产品可靠性的工程可靠性稳健设计方法。针对实际工程中很难确定极限状态函数的显性表达式、随机有限元法的局限性和响应面法存在的理论精度问题,张义民等[3]运用神经网络与随机摄动技术,提出了基于神经网络的机械零部件的可靠性稳健设计理论。但利用神经网络训练样本时,样本的数量及分布直接决定其计算的精度,难以达到预期的设计要求[4]。刘仁云等[5]运用灰色粒子群算法对汽车后桥进行了可靠性稳健设计。粒子群算法虽然新颖、简单,应用方便,但用粒子群算法解答多目标问题时,因灰色关联理论本身存在固有的缺陷,不可避免地会出现“早熟”现象[6]。Jamali等[7]使用多目标一致多样性遗传算法对线性状态反馈控制器进行了可靠性稳健Pareto设计,取得了较好效果。但迄今为止,作为改进遗传算法提出的免疫遗传算法,相关优化设计的参考文献甚少,究其原因,主要在于:
(1) 记忆池更新与设置方式尚有问题。在免疫遗传算法中,一个最重要的概念是期望繁殖率,它与抗体浓度成反比。对于相似抗体,浓度增加,选择其参与交配的概率就会降低。现有文献一般采用将子代抗体全部引入记忆池,却没有意识到记忆池对曾出现的抗体具有记忆功能,故对于适应值较优的个体,当记忆池中存在相似于子代个体的父代抗体时,将其引入后,势必提高其浓度,降低该较优个体参与交配的概率,减缓其进化速度,且一般未对记忆池进行分区处理,操作起来很不方便。
(2) 没有采用免疫代谢策略。当记忆池中保留着各代中期望繁殖率较低的个体时,就会使免疫系统的免疫能力低下,从而延长计算时间,减慢收敛速度。
(3) 相似性比较的方式不良。在计算抗体相似性时,当今绝大多数文献均采用欧氏距离作为相似性指标[8-9],事实上,其计算效率比反映抗体品质相似性指标的计算效率低[10]。
(4) 募集新成员的方式不对。募集新成员时,一般只考虑到与现有抗体的相似性,并没有考虑新成员彼此之间的相似性[9],从而有可能引入彼此相似的个体,致使其选择受到限制。
(5) 精英保留策略尚有问题。精英保留策略是为使精英个体不因选择、交叉与变异操作造成丢失或破坏[11],让其不参与配对交叉而直接去替换下一代中的最差个体[12]。因记忆池对出现过的抗体具有记忆功能,故精英个体已保留在记忆池中,无需再采用保留策略,让其直接参与进化即可。
(6) 交配策略不佳。目前,现有免疫遗传算法均采用轮盘赌策略将随机挑选出来的2个个体进行交配的方式,故期望繁殖率高的优秀个体不一定参与了交配,且得不到额外的交配机会。况且一般将所有群体作为一个整体看待,根本没有采用能加快算法收敛性的小生境技术[13]。
正是由于上述原因,致使现有免疫遗传算法的收敛性往往较差。为此,本文作者先对免疫遗传算法进行改进,然后将其应用于土压平衡盾构机三级行星减速器轴的优化,以验证该算法的可行性及其效果。
1 可靠性及其灵敏度分析
1.1 可靠性分析的随机摄动法
机械零部件的可靠度可表示为[14]:
 (1)
(1)
式中:f(x)为基本随机参数向量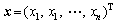 的联合概率密度函数,其参数为载荷或表示零部件特征的随机量;
的联合概率密度函数,其参数为载荷或表示零部件特征的随机量; {x|g(x)>0};g(x)为功能函数或状态函数,零部件的2种状态为:
{x|g(x)>0};g(x)为功能函数或状态函数,零部件的2种状态为:
 (2)
(2)
因零部件可靠性稳健设计要求可靠度对设计参数的变化不敏感,为此,不妨把随机参数向量x和功能函数g(x)表示为:
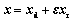 (3)
(3)
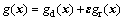 (4)
(4)
其中: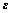 为一数值较小的参数,下标为d的部分表示随机参数的确定部分;下标为r的部分表示随机参数的随机部分,且其均值为0。可见,随机部分比确定部分小得多。对式(3)~(4)分别取均值、方差、三阶矩与四阶矩,有:
为一数值较小的参数,下标为d的部分表示随机参数的确定部分;下标为r的部分表示随机参数的随机部分,且其均值为0。可见,随机部分比确定部分小得多。对式(3)~(4)分别取均值、方差、三阶矩与四阶矩,有:
 (5)
(5)
 (6)
(6)
其中: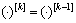
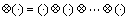 为
为 的Kronecker幂,
的Kronecker幂,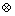 代表Kronecker积,且有
代表Kronecker积,且有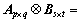
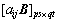 ;Var(x)为基本随机参数的方差。据矩阵导数的定义:
;Var(x)为基本随机参数的方差。据矩阵导数的定义:

将g(x)用Taylor公式在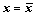 附近展开到一阶为止,有:
附近展开到一阶为止,有:
 (7)
(7)
将式(7)代入式(6),得:
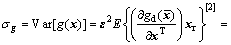
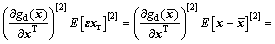
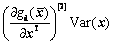 (8)
(8)
同理,
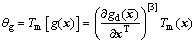 (9)
(9)
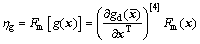 (10)
(10)
将状态函数g(x)对基本随机变量矢量x求偏导数,有
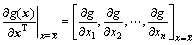 (11)
(11)
把式(11)代入式(8)~(10),即可得状态函数的方差、三阶矩与四阶矩的表达式。
据可靠性指标的定义,有
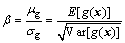 (12)
(12)
这样,就可以利用可靠性指标直接衡量构件的可靠性,有
 (13)
(13)
式中: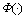 为标准正态分布函数。
为标准正态分布函数。
由上面的推导过程可知:就状态函数g(x),可靠性指标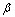 即为标准化的随机变量,根据Edgeworth级数,其概率分布函数可近似展开成标准正态分布函数,即
即为标准化的随机变量,根据Edgeworth级数,其概率分布函数可近似展开成标准正态分布函数,即

 (14)
(14)
式中: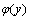 为标准正态分布函数
为标准正态分布函数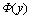 的概率密度函数;
的概率密度函数;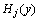 为Hermite多项式。其递推公式为:
为Hermite多项式。其递推公式为:
 (15)
(15)
由式 (14)可知:把概率分布未知的功能函数展开成标准正态分布的表达式时,其概率密度函数一般不对称。故系统的可靠度可表示为:
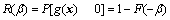 (16)
(16)
显然,式(16)就是式(1)的近似表达式。然而,用式(16)计算可靠度时,有时会出现R>1的情况,此时,不妨采用下述经验公式进行修正:
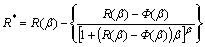 (17)
(17)
由于Edgeworth级数可精确逼近任意随机变量的真实分布,且在推导过程中,无需对随机参数的分布类型与激励类型作任何限制,故其结果很接近于工程实际。通常,Edgeworth级数的前4项就已经有较高的精度,完全可以满足一般工程实际的需要,故本文不妨也取式 (14)的前4项进行可靠度计算及其灵敏度分析。
1.2 可靠性设计的灵敏度分析
由前面分析可知,本文的设计是针对基本随机参数矢量x的均值点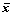 而言的,故在均值点
而言的,故在均值点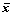 附近,可靠度对x的均值与方差的灵敏度为:
附近,可靠度对x的均值与方差的灵敏度为:
 (18)
(18)
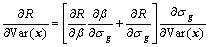 (19)
(19)
其中,利用式(15)可得:
 (20)
(20)
由式(16), (14)与式(20)可得:
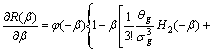

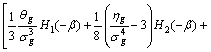
 (21)
(21)
 (22)
(22)
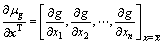 (23)
(23)
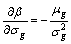 (24)
(24)

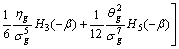 (25)
(25)
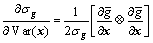 (26)
(26)
把已知条件与可靠性分析的计算结果代入式(18)与式(19),即得可靠度的灵敏度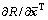 与
与 。
。
然而,当可靠度R>1时,可靠度对可靠性指标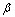 的灵敏度为
的灵敏度为
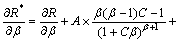
 (27)
(27)
其中: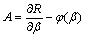 ;
; 。
。
2 优化模型
为使设计的结构具有良好的稳健性,不因外界噪声而出现较大波动,要求结构对设计参数的灵敏度越小越好。在满足此条件的同时,再尽量满足经济性指标如结构轻量化等要求,为此,建立如下2个目标 函数。
(1) 根据前面的建模思想,以可靠度对设计变量均值点处的联合灵敏度最小为第1个目标函数,有

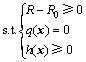 (28)
(28)
其中: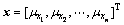 ;R0为应满足的可靠度;R为由上述Edgeworth级数或经验修正公式计算获得的可靠度;q(x)为等式约束矩阵;h(x)为不等式约束 矩阵。
;R0为应满足的可靠度;R为由上述Edgeworth级数或经验修正公式计算获得的可靠度;q(x)为等式约束矩阵;h(x)为不等式约束 矩阵。
(2) 对于经济性指标如体积最小的问题,建立第2个目标函数:

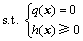 (29)
(29)
其中:V为结构的体积。
与体积相比,可靠性灵敏度函数值(一般为0~1)无疑要小得多。故当将其化为单目标时,处理起来很不方便,为此,提出如下模型:
 (30)
(30)
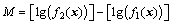 (31)
(31)
其中:lg为常用对数;[ ]为高斯取整符号。
这样,无论设计变量x如何变化,新的函数值 与函数值f2(x)始终处于同一数量级,即可自适应地对函数值进行调整,以实现目标之间的动态平衡。从而,就可以用
与函数值f2(x)始终处于同一数量级,即可自适应地对函数值进行调整,以实现目标之间的动态平衡。从而,就可以用 代替原来的f1(x)进行后续操作。
代替原来的f1(x)进行后续操作。
上述模型不仅可以实现两目标之间的动态平衡,对于3个以上目标函数的情况,也同样适应。为此,可以根据像集法,将其转变成如下单目标问题:
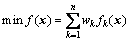
 (32)
(32)
式中:wk≥0为分目标函数fk(x)的加权因子,取决于各分目标函数值的数量级及其重要程度,可采用加权组合法中的像集法来确定加权因子wk,即
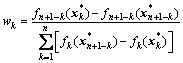 ;k=1, …, n (33)
;k=1, …, n (33)
式中:n为分目标函数的个数;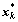 为第k个分目标的最优解向量。
为第k个分目标的最优解向量。
3 免疫遗传算法
免疫遗传算法是借鉴生物免疫系统中抗体浓度的控制原理提出的一种改进遗传算法[15]。它将生物免疫系统中抗体的多样性、自我调节能力、免疫记忆能力等特征引入遗传算法后,就可将全局搜索能力、局部搜索能力和搜索速度3方面同时兼顾起来,因而成为优化设计领域的研究热点之一。免疫遗传算法把待求问题的目标函数对应为抗原,问题的解对应为抗体,用抗原和抗体之间的亲和力来描述可行解与最优解的逼近程度。
由上述可知,抗体代表问题的一组解,故抗体可表示为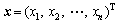 。抗体是由各个基因构成的,该解向量中的各变量与抗体各基因的对应关系见图1。
。抗体是由各个基因构成的,该解向量中的各变量与抗体各基因的对应关系见图1。

图1 典型抗体与解向量间的对应关系
Fig.1 Corresponding relationship between typical antibody and solution vectors
显然,图1不仅阐明了各设计变量与抗体各基因之间的一一对应关系,易于理解,而且因每一基因仅有1个变量与之对应,易于理解优化中疫苗接种的概念,便于设计专门的免疫遗传算子来处理约束条件。
3.1 免疫遗传算子
为便于处理设计变量的约束,保证抗体在进化过程中一直处于可行域内,专门引入2种免疫遗传算子:凸组合算术交叉算子与非一致变异算子[9]。
3.1.1 凸组合算术交叉算子
凸组合算术交叉算子是指由2个个体的某种线性组合生成新个体的繁殖操作,且能保证所生成的新个体的各个分量均位于可行域内。任取2个抗体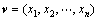 和
和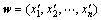 ,若选择其中的第k个分量进行线性组合,有
,若选择其中的第k个分量进行线性组合,有
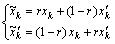 (34)
(34)
其中:k=1, 2, …, n。故生成的新个体为 和
和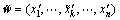 。其中,r为[0, 1]内服从均匀分布的随机数。
。其中,r为[0, 1]内服从均匀分布的随机数。
3.1.2 非一致变异算子
非一致变异算子是一种动态变异算子,它能有效提高实数编码的精细调节能力,提高算法的局部搜索能力。若实数基因xk被选为非一致变异算子,则变异后的值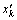 为
为
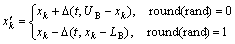 (35)
(35)
式中:round(rand)表示对0~1之间的随机数四舍五入取整;LB和UB分别为变量xk的下界和上界,t为进化代数,函数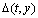 可定义为
可定义为
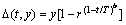 (36)
(36)
式中:r为[0, 1]内服从均匀分布的随机数;T为最大进化代数;b为可调参数,它决定了随机扰动对进化代数t的依赖程度,此处,取b=6。由式(36)可知:函数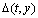 是一个位于区间[0, y]内的值,随着进化代数t的增加,
是一个位于区间[0, y]内的值,随着进化代数t的增加,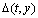 单调递减,且最终趋于0。这一性质可使算子在运行初始阶段(t较小时)进行全局搜索,而在进化后期(t接近于T时)进行局部搜索。
单调递减,且最终趋于0。这一性质可使算子在运行初始阶段(t较小时)进行全局搜索,而在进化后期(t接近于T时)进行局部搜索。
3.2 免疫选择算子
为保证抗体群的多样性,有效抑制遗传算法的“早熟”现象,提高算法的全局搜索能力,借鉴生物免疫系统中抗体的动态平衡维持机制提出免疫选择算子。为便于理解,不妨先介绍几个相关概念。
定义1:亲和力(affinity)是指抗体与抗原的匹配程度。反映在优化问题上,如果待优化的目标函数是求最大值,则可将亲和力定义为目标函数值,反之,则将其定义为目标函数值的倒数。在本文中,将抗体vi的亲和力定义为
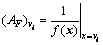 (37)
(37)
定义2:在规模为N的特定抗体群中,假设每个抗体都可表示成n个分量的n维向量,从中任取2个抗体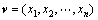 和
和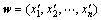 ,其适应值分别为fv和fw,假定ε>0适当小,若
,其适应值分别为fv和fw,假定ε>0适当小,若
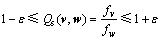 (38)
(38)
成立,则称抗体v与w相似。其中, 是反映抗体v与w品质相似性的指标(此处,品质是指其适应值,对于求最小值问题,适应值越小的抗体其品质越好),ε为抗体相似度阈值,譬如,当取ε=0.01时,若式(38)成立,则说明抗体v与抗体w在品质上有99%的相似性。
是反映抗体v与w品质相似性的指标(此处,品质是指其适应值,对于求最小值问题,适应值越小的抗体其品质越好),ε为抗体相似度阈值,譬如,当取ε=0.01时,若式(38)成立,则说明抗体v与抗体w在品质上有99%的相似性。
定义3:浓度(concentration)是指抗体及其相似抗体在种群中所占的比例,其数学描述为
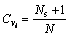 (39)
(39)
其中: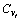 为抗体vi的浓度;Ns是抗体群中相似于vi的抗体数;N为种群规模。
为抗体vi的浓度;Ns是抗体群中相似于vi的抗体数;N为种群规模。
定义4:免疫选择是指一种综合考虑抗体浓度与亲和力、按概率随机选择的方式,其数学描述可表 示为
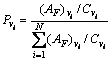 (40)
(40)
其中: 为抗体
为抗体 的期望繁殖率;
的期望繁殖率;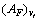 为抗体
为抗体 与抗原之间的亲和力;
与抗原之间的亲和力;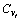 为抗体
为抗体 的浓度。从式(40)可以看出:当抗体浓度一定时,亲和力越大,抗体被选择的概率越大;而当亲和力一定时,抗体浓度越高,抗体被选择的概率却越小(即抑制),反之,被选择的概率则越高(即促进)。为此,可以根据抗体与抗原之间亲和力及抗体浓度,选择亲和力大、浓度低的抗体进行交叉与变异而产生新的种群。亲和力大可确保较优抗体繁殖再生,保持解的优良模式;而浓度低能维持种群的多样性,保证解的分布性,故与遗传算法相比,免疫遗传算法具有更强的学习能力,可避免早熟现象。
的浓度。从式(40)可以看出:当抗体浓度一定时,亲和力越大,抗体被选择的概率越大;而当亲和力一定时,抗体浓度越高,抗体被选择的概率却越小(即抑制),反之,被选择的概率则越高(即促进)。为此,可以根据抗体与抗原之间亲和力及抗体浓度,选择亲和力大、浓度低的抗体进行交叉与变异而产生新的种群。亲和力大可确保较优抗体繁殖再生,保持解的优良模式;而浓度低能维持种群的多样性,保证解的分布性,故与遗传算法相比,免疫遗传算法具有更强的学习能力,可避免早熟现象。
3.3 免疫策略
为维持进化过程中抗体群的动态平衡,进一步提高算法快速搜索最优解的性能,限制某一空间相似抗体的过度繁殖,保持抗体群的多样性,根据物以类聚、人以群分的原则,特提出如下6种免疫策略。
(1) 募集新成员。募集新成员是指在抗体空间里随机产生一些新的彼此不相似、与现有抗体也不相似的抗体插入抗体群,它起到维持群体的动态平衡、微调群体多样性的作用,从而可提高算法的全局搜索能力。
(2) 记忆池及其抗体的更新。为模仿生物免疫系统的免疫记忆功能,在算法中设置记忆池。记忆池中的抗体是算法进化到当前为止所获得的较优解,且它们将随着抗体群的进化而逐步被更优的个体所取代。记忆池的作用是为系统或相似问题的求解提供初始个体,并使算法具有快速搜索最优解的性能。有时,可根据实际需要,对记忆池进行分区处理,以便将抗体分类存储。
(3) 免疫代谢。模拟免疫行为中细胞的混沌增殖现象[16],找出记忆池中期望繁殖率低的个体并予以剔除(可将超过种群规模的个体踢除,也可按5%进行衰减),从而提高了免疫系统的免疫能力。
(4) 小生境技术。小生境技术就是借鉴生物生存与进化过程中的小生境思想,将记忆池中的全部个体分成若干类,再在每类中进行免疫选择、交叉与变异操作而产生新一代抗体群[17]。因每个小生境相对独立,故各子群体可并行进化, 从而这一技术可保持抗体群的分布性,具有很强的全局寻优能力,能加快种群的进化。
(5) 交配策略。采用对期望繁殖率最高的个体执行确定选择而对其余个体执行随机选择的原则,即在每个小生境内,采取将期望繁殖率最高的个体作为交配中的雄性方,不经选择而直接参与交配,而其余个体须参与随机选择,将挑选出来的个体全部作为雌性方看待(对于没有参与交叉的个体,则直接以子代身份加入子代群体),并采取与期望繁殖率最高的雄性方交叉的交配策略,这样,每次产生的新个体就有2或2以上的偶数个,且每个小生境内的最优个体不仅参与了交叉配对,还获得了更多的交配机会,故比遗传算法的轮盘赌策略有更快的收敛速度,且切实可行。
(6) 精英策略。因记忆池对曾出现的抗体具有记忆的潜力,故精英个体已保留在记忆池中,无需再采用保留策略,让其直接参与进化即可。这样,精英个体的优秀基因就在下一代或下几代中得到延续,从而加快了种群的进化。
3.4 免疫算法的实现机理
对上述算法的基本思想,可采用如下步骤来实现。
(1) 确定种群初始规模N、选择概率Ps(用于雌性个体的选择)、交叉概率Pc、变异概率Pm、相似度阈值ε与终止进化代数T,并将记忆池一分为二,分别设为Mset1和Mset2。
(2) 初始抗体群的产生、存储与分类排序。在可行域内随机产生N个抗体构成初始抗体群A0,令t=0,计算每个抗体的适应值、亲和力、浓度及期望繁殖率,采用沉底法,将各个抗体的相关参数按照期望繁殖率P从高到低排列,并将其存储在空记忆池的一分区Mset1中,然后将Mset1中的N个抗体存入A1。
(3) 下一代抗体群的产生。将A1中的抗体按照期望繁殖率由高到低分成若干组,每组对应一个小生境,让抗体在各个小生境内根据交配策略进行免疫选择与交叉后再进行变异操作,而得到下一代抗体群C。
(4) 募集新成员。在可行域内随机产生M个(可参照免疫代谢的标准)彼此不相似且与C中的抗体也不曾相似的抗体,并将其引入C。
(5) 记忆池的更新。先对Mset1中的抗体进行免疫代谢处理,并将代谢后的抗体存入记忆池的另一分区Mset2,再将C中的抗体与Mset2中的抗体进行相似性比较,如果存在相似抗体,则用C中的抗体替换Mset2中相似性最高的抗体,否则将C中的抗体引入记忆池的二分区Mset2。
(6) 抗体的转存与替换。计算Mset2所有抗体的亲和力、浓度与期望繁殖率,并按照期望繁殖率由高到低排列后存入Mset1中,将Mset1中的抗体数作为新的种群规模N,并用其中的全部抗体去替换A1中的所有抗体,再将全部抗体按适应值作降序排列,并令t=t+1。
(7) 终止检验。若满足终止条件(通常为预设的运算精度或终止进化代数),则终止检验,A1中适应值最低的抗体即为所求,将其变量值输出即可;否则,返回(3)。
鉴于免疫策略较多(共6条),各算法步骤之间的逻辑关系又比较复杂,特将上述算法步骤用图2进行详细描述,以便于理解与实际操作。图2中:P为期望繁殖率,N为种群规模,A0与A1表示父代,C表示子代;在募集新成员过程中,只将那些彼此不相似且与现有抗体也不相似的抗体引入抗体群,这样才能起着微调群体多样性的作用。Mset2更新时,对不相似于Mset2中抗体的子代个体,将其引入Mset2,而对相似于Mset2中抗体的子代个体,则用子代个体去替换Mset2中相似性最高的个体,这样,不但使Mset2中种群的多样性增加,使算法具有更强的免疫力,而且使Mset2中原有抗体不会因新抗体的引入而使其浓度提高致使其选择受到抑制。
由图2可知:根据期望繁殖率的不同,将抗体群分组后,每组分别对应一个不同的小生境。若第1个小生境有n1个抗体,则将整个种群内期望繁殖率最高的前n1个抗体安置在第1个小生境内;若第2个小生境有n2个抗体,则将整个种群内期望繁殖率按降序排名在n1+1~ n1+ n2的抗体安置在第2个小生境内,依此类推。抗体的这种安置方式使优秀程度相近的抗体能集聚在一起进行交叉,且在每个小生境内,期望繁殖率最高的雄性个体可与1个甚至多个雌性个体参与交配(注意:当挑选出来的雌性个体数n>1时,须克隆n-1雄性个体后方可与雌性个体一一配对交叉),产生的子代个体数就为2或2以上的偶数,无疑加快了种群的进化。
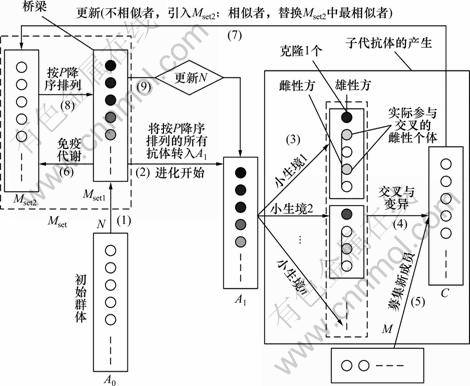
图2 免疫遗传算法实现逻辑关系图
Fig.2 Logic relation diagram of achieving IGA
值得注意的是:虽然抗体在Mset1与Mset2之间来回周旋,但同一抗体并非在2个记忆分区同时出现(即存在时间差,或者说,当一记忆分区有抗体时,另一记忆分区就是空的),因此,记忆池中的抗体数没有因分区而发生改变。但从上述分析可知:将记忆池一分为二,明显便于理解与操作。
4 数值算例
已知某土压平衡式盾构机的3级行星减速器,输入转矩Ts=1 489 N·m,输入转速为1 145.6 r/min,轴是空心的,如图3所示,轴用材料为17CrNi2MoAl,其屈服强度为σs= 690 MPa,许用剪切应力τs按最大剪应用理论计算,即τs=0.5σs[18]。每级扭矩均通过花键传递给轴,各设计参数及其取值见图3与表5中优化前的部分,要求在确保可靠度R0≥0.95 000 (即可靠性指标β≥4.26)的条件下,实现轴的轻量化设计的同时,使可靠度对设计变量的灵敏度最低。

图3 在扭矩作用下的空心轴
Fig.3 Hollow shaft loaded in torque
在实际工程中,轴的几何尺寸与材料特性一般服从正态分布的随机变量。设其基本随机变量矢量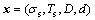 ,其中,轴的外径D与内径d是相关随机变量,其相关系数ρ=0.7[14],其余基本随机变量均相互独立。
,其中,轴的外径D与内径d是相关随机变量,其相关系数ρ=0.7[14],其余基本随机变量均相互独立。
在扭矩传递过程中,作用在各级行星齿轮轴上的扭矩Ts存在着如下关系[19]:
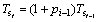 (i=2, 3),
(i=2, 3),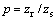 (41)
(41)
其中:zs与zr的意义及取值见表1。
表1 太阳轮与内齿圈在各级中的齿数
Table 1 Teeth size of central and inner gear in each stage 个

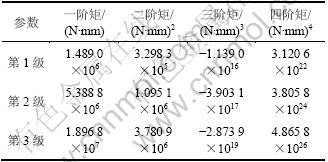
因轴所受扭矩的分布概型未知,不妨采用抽样统计的方式,即通过扭矩传感器对输入端的扭矩进行采样后,据式(41)即可求得1~3级轴所受扭矩Ts的前四阶矩,如表2所示。
表2 各级轴的前四阶矩
Table 2 First four moments of every stage shaft
(1) 确定设计变量。因盾构机行星减速器每级轴的长度均由相关结构参数确定,故只有轴的外径D与内径d这2个设计变量,即设计变量 。
。
(2) 建立力学模型。因行星减速器轴较短,不妨忽略其重力产生的弯矩,而只考虑其在扭矩作用下产生的剪应力,有
 ,
, ,
,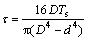 (42)
(42)
式中:Ts为太阳轮所传递的扭矩;W为轴的抗扭截面模量;D为轴的外径;d为轴的内径。
在考虑一定安全裕度的条件下(安全系数S的取值见表3),根据应力-强度干涉理论,以剪应力极限状态表示的状态方程为:
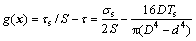 (43)
(43)
其中: ;
; 为材料的屈服强度。
为材料的屈服强度。
(3) 建立数学模型。
① 目标函数的确定。
a. 根据前面的建模思想,以可靠度对设计变量均值的灵敏度最小为第1个目标函数,则有
 (44)
(44)
其中: 。
。
表3 各级安全系数与材料变异系数取值
Table 3 Coefficient of safety and material variance in every stage

b. 对轴的质量最小即体积最小的问题,由于每级轴的长度已经确定,故只需求横截面的面积最小即可,故第2个目标函数为:
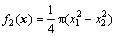 (45)
(45)
然后,再按前面化多目标为单目标的方法将其转变为单目标即可。
② 约束条件的确定。
a. 行星减速器1~3级轴的内径d与外径D的定义域及其变系数的取值如表4所示。
表4 设计变量的定义域与变异系数
Table 4 Domain of design variables and their coefficient of variation
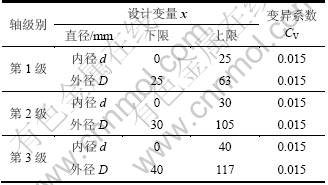
b. 要求可靠度指标β≥4.26。
c. 因盾构机行星减速器时常受到各种冲击载荷的作用,要求在一般载荷作用下,其可靠度对设计变量的灵敏度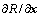 ≤10-6。
≤10-6。
(4) 优化求解。对于轴在优化前的外径与内径,以及用免疫遗传算法所获取的任意一组实数值,如外径与内径分别为[63, 15] mm,不妨将其看成是对外径与内径分别约为63 mm与15 mm的轴进行n=100次测量后由测量值所求得的均值μ,设其变异系数CV= [0.015, 0.015],则可求出该组测量值的方差σ,若它们均服从正态分布,就可求出其三阶矩与四阶矩。
采用本文所改进的免疫遗传算法,根据上述数学模型编写MATLAB程序进行求解。同时,为了阐明算法改进后的优越性,采用与改进前的算法作对照,见图4~6(其中:t为进化代数,fm为各代中的最优适应值)。
从图4~6可以看出:与改进前相比,本文所提出的改进免疫遗传算法不仅具有更快的收敛速度,还具有更高的收敛精度。
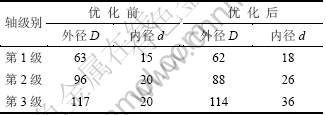
上述程序运行所得自洽最优解如表5所示(表中数据是采用向上取整法,对优化后轴的外径与内径直接取整)。同时,将优化前各级轴的尺寸列于表5,以便对照。
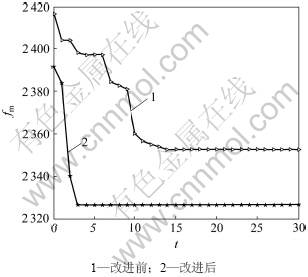
图4 IGA改进前后优化第1级轴的收敛性比较
Fig.4 Convergence comparison between unimproved and improved IGA for the 1st shaft
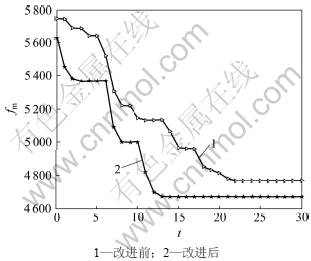
图5 IGA改进前后优化第2级轴的收敛性比较
Fig.5 Convergence comparison between unimproved and improved IGA for the 2nd shaft
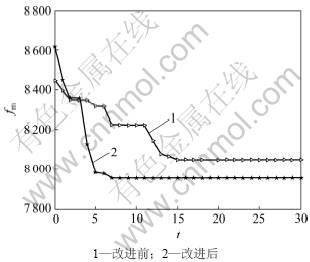
图6 IGA改进前后优化第3级轴的收敛性比较
Fig.6 Convergence comparison between unimproved and improved IGA for the 3rd shaft
表5 优化前后各级轴尺寸对照
Table 5 Size contrast of shafts before & after optimization mm
(5) 将上述程序运行所得轴的可靠性指标、可靠度及可靠性灵敏度见表6。此外,再采集109个样本,运用Monte Carlo法计算其可靠度,将其结果也列于表6,以便与根据本文算法求得的可靠度进行对照。
从表6~7可知:据本文算法求得的各级轴的可靠性指标β不仅均大于给定值4.26,而且各级轴的可靠度对设计变量的灵敏度均满足条件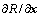 ≤10-6,各级轴的可靠度也均大于对应Monte Carlo法得到的可靠度,这说明轴的可靠性可以得到保证,同时也说明本文所创建的力学与数学模型、改进的算法及求解策略的正确性。
≤10-6,各级轴的可靠度也均大于对应Monte Carlo法得到的可靠度,这说明轴的可靠性可以得到保证,同时也说明本文所创建的力学与数学模型、改进的算法及求解策略的正确性。
表6 优化后各级轴的强度
Table 6 Strength of each shaft after optimization

表7 优化后各级轴的可靠性灵敏度
Table 7 Reliability sensitivity of each shaft after optimization

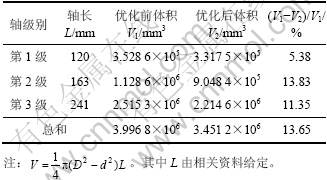
优化前、后各级轴的体积及其减少率见表8。由表8可知:三级行星减速器三根轴的总体积减少率为13.65%,说明采用本文提出的改进IGA能取得较好的优化效果。
表8 优化前后轴的体积及其减少率
Table 8 Volume and its reduction rate before & after optimization
5 结论
(1) 提出了实现目标函数值之间保持动态平衡问题的全新模型,实现了目标函数与像集法的结合。不管多目标函数的个数、函数值之间的悬殊程度、化多目标为单目标的方法,应用此模型均可达到目的。
(2) 在澄清免疫遗传算法基本概念的同时,不仅使每个小生境内的优秀个体获得了更多的交配机会,而且精英个体也参与了进化,从而使其优秀基因在下一代或下几代中得到了延续,加快了算法的收敛性,改进了免疫遗传算法。
(3) 解决了设计变量在任一点处求其前四阶矩的方法,顺利将免疫遗传算法与可靠性及其灵敏度分析衔接起来,并用它求解含有四阶矩技术的复杂偏微分方程,拓宽了算法的应用领域,表明该算法在解答大型复杂系统时也具有良好的应用前景。
(4) 创建了可靠度对设计变量灵敏度最低与体积最小的两目标优化模型,利用本文所提出的改进免疫遗传算法对三级行星减速器的轴进行求解验证。优化结果表明:该算法的鲁棒性可使轴的总体积减小13.65%,与改进前相比,改进后的免疫遗传算法有更快的收敛速度与更高的收敛精度。
参考文献:
[1] Harish A l, Renaud J E, Evan L P, et al. Uncertainty quantification using evidence theory in multidisciplinary design optimization[J]. Reliab Eng Syst Safe, 2004, 85: 281-294.
[2] Ioannis D, ZHAN Kang. Robust design of structures using optimization methods[J]. Computer Methods Appl Mech Engrg, 2004, 193(8): 2221-2237.
[3] 张义民, 高娓, 宋相强, 等. 具有应力集中的机械零件可靠性稳健设计[J]. 工程力学, 2008, 25(11): 237-240.
ZHANG Yi-min, GAO Wei, SONG Xiang-qiang, et al. Reliability-based robust design for mechanical components with stress concentrations[J]. Engineering Mechanics, 2008, 25(11): 237-240.
[4] 琚亚平, 张楚华. 利用试验设计法建立翼型气动特性的人工神经网络模型[J]. 航空学报, 2010, 31(5): 893-898.
JU Ya-ping, ZHANG Chu-hua. Artificial neural network model of airfoil aerodynamic performance using design of experiments[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 893-898.
[5] 刘仁云, 张义民, 刘巧伶. 基于多目标优化策略的结构可靠性稳健设计[J]. 应用力学学报, 2007, 24(1): 267-271.
LIU Ren-yuan, ZHANG Yi-ming, LIU Qiao-ling. Structural robust reliability design for multi-objective optimization[J]. Chinese Journal of Applied Mechanics, 2007, 24(1): 267-271.
[6] 张干清, 龚宪生, 王欢欢, 等. 基于可靠灰色粒子群算法的盾构机行星减速器轮系的多目标优化设计[J]. 机械工程学报, 2010, 46(23): 135-145.
ZHANG Gan-qing, GONG Xian-sheng, WANG Huan-huan, et al. Multi-objective optimization design on gear train of planetary reducer in shield tunneling machine based on reliably grey particle swarm optimization[J]. Journal of Mechanical Engineering, 2010, 46(23): 135-145.
[7] Jamali A, Hajiloo A, Nariman Z. Reliability-based robust pareto design of linear state feedback controllers using a multi-objective uniform-diversity genetic algorithm[J]. Expert Systems with Applications, 2010, 37(1): 401-413.
[8] Das S, Abraham A, Konar A. Automatic kernel clustering with a multi-elitist particle swarm optimization algorithm[J]. Pattern Recognition Letters, 2008, 29(5): 688-699.
[9] 陈文英, 阎绍泽, 褚福磊. 免疫遗传算法在智能桁架结构振动主动控制系统优化设计中的应用[J]. 机械工程学报, 2008, 44(2): 196-200.
CHEN Wen-ying, YAN Shao-ze, CHU Fu-lei. Immune genetic algorithm used to integrated optimal design of active vibration control system for piezoelectric intelligent truss structures[J]. Journal of Mechanical Engineering, 2008, 44(2): 196-200.
[10] 陈曦, 谭冠政, 江斌. 基于免疫遗传算法的移动机器人实时最优路径规划[J]. 中南大学学报: 自然科学版, 2008, 39(3): 577-583.
CHEN Xi, TAN Guan-zheng, JIANG Bin. Real-time optimal path planning for mobile robots based on immune genetic algorithm[J]. Journal of Central South University: Science and Technology, 2008, 39(3): 577-583.
[11] Dehuri S, Patnaik S, Ghosh A, et al. Application of elitist multi-objective genetic algorithm for classification rule generation[J]. Applied Soft Computing, 2008, 8(1): 477-487.
[12] LIU Yang. Automatic calibration of a rainfall-runoff model using a fast and elitist multi-objective particle swarm algorithm[J]. Expert Systems with Applications, 2009, 36(5): 9533-9538.
[13] 张京军, 崔炜, 王南. 小生境遗传算法的多刚体系统动力学参数优化设计[J]. 机械工程学报, 2004, 40(3): 66-70.
ZHANG Jing-jun, CUI Wei, WANG Nan. Niche genetic algorithm for optimization design of dynamic parameters of rigid multi-body systems[J]. Journal of Mechanical Engineering, 2004, 40(3): 66-70.
[14] 张义民. 任意分布参数的机械零件的可靠性灵敏度设计[J]. 机械工程学报, 2004, 40(8): 100-105.
ZHANG Yi-min. Reliability sensitivity design for mechanical elements with arbitrary distribution parameters[J]. Journal of Mechanical Engineering, 2004, 40(8): 100-105.
[15] 李秀卿, 汪海, 许传伟, 等. 基于免疫遗传算法优化的神经网络配电网网损计算[J]. 电力系统保护与控制, 2009, 37(11): 36-39.
LI Xiu-qing, WANG Hai, XU Chuan-wei, et al. Calculation of line losses in distribution systems using artificial neural network aided by immune genetic algorithm[J]. Power System Protection and Control, 2009, 37(11): 36-39.
[16] 罗小平, 韦巍. 一种基于生物免疫遗传学的新优化方法[J]. 电子学报, 2003, 31(1): 59-62.
LUO Xiao-ping, WEI Wei. A new optimization method on immune genetics[J]. Acta Electronical Sinica, 2003, 31(1): 59-62.
[17] LIU Xi-yu, LIU Hong, DUAN Hui-chuan. Particle swarm optimization based on dynamic niche technology with applications to conceptual design[J]. Advances in Engineering Software, 2007, 38(10): 668-676.
[18] 成大先. 机械设计手册: 第1卷[M]. 5版. 北京: 化学工业出版社, 2008: 1-102.
CHENG Da-xian. Mechanical design handbook: Volume 1[M]. 5th ed. Beijing: Chemical Industry Press, 2008: 1-102.
[19] 饶振纲. 行星齿轮传动设计[M]. 北京: 化学工业出版社, 2003: 143.
RAO Zhen-gang. Design on planetary transmission[M]. Beijing: Chemical Industry Press, 2003: 143.
(编辑 陈灿华)
收稿日期:2011-10-18;修回日期:2011-03-06
基金项目:国家高技术研究发展计划(“863”计划)重点项目(2007AA041802);重庆市科技攻关计划项目(CSTC, 2007AC3015);重庆大学机械传动国家重点实验室自主研究基金资助项目(0301002109137)
通信作者:龚宪生(1956-),男,重庆人,博士,教授,博士生导师,从事机械振动分析及控制、机械传动智能化设计及应用研究;电话:13062333307;E-mail: xsgong@cme.cqu.edu.cn