基于等效Mohr-Coulomb摩擦角的强度准则主应力平面表示

姜华

(长安大学 公路学院，陕西 西安，710064)

摘要：定义Mohr-Coulomb(M-C)强度准则各种表达式和对应的等效M-C摩擦角，基于等效M-C摩擦角给出主应力σ₁-σ₂关系表达式，即各种强度准则在主应力平面的表示。以Matsuoka-Nakai(M-N)，Lade-Duncan(L-D)和Moji强度准则为例，演示了该方法的应用，研究3种强度准则中间主应力σ₂对材料屈服时的最大主应力σ₁的影响。结果表明：这种在二维主应力σ₁-σ₂平面中表示强度准则的新方法既适用于无黏性材料又适用于黏性材料，用于黏性材料时，通过平移坐标轴将黏性材料破坏面转换成无黏性材料破坏面，为材料强度准则研究提供了新思路。

关键词：M-C准则；M-N准则；L-D准则；Moji准则

中图分类号：TU47          文献标志码：A         文章编号：1672-7207(2012)08-3216-06

Expressing strength criterion in principal stress plane base on equivalent Mohr-Coulomb friction angle

JIANG Hua

(School of Highway, Chang’an University, Xi’an 710064, China)

Abstract: Different expressions for the Mohr-Coulomb(M-C)criterion and the definitions of the equivalent M-C friction angle were defined. The expression about the relationship between principal stresses σ₁ and σ₂, derived from the equivalent M-C friction angle was given further. The strength criterion was expressed in the principal stress plane. The Matsuoka-Nakai(M-N), Lade-Duncan(L-D) and Moji criteria were used as application examples to demonstrate the proposed method, and the influence of the intermediate principal stress σ₂ to the yield strength σ₁ of the material was studied. The results show that this new method is suitable for both cohesionless and cohesive materials. The failure surface for cohesive materials transforms to the failure surface for cohesionless materials through translation of the coordinates’ system for cohesive materials, which provides a new idea for research strength criterion.

Key words: M-C criterion; M-N criterion; L-D criterion; Moji criterion

材料强度准则指材料在多轴应力下发生破坏的数学描述，对构造三维本构关系模型非常重要。以一维状态下的应力-应变关系曲线为例，材料强度对应于曲线的峰值应力。自20世纪初Mohr-Coulomb(简称M-C)强度准则提出以来，工程界涌现了大量的强度准则^[1-5]。新强度准则通常基于已有强度准则存在的不足提出，如M-C准则虽然在岩土工程中得到了广泛运用，但不能考虑材料的中间主应力效应导致在很多情况下低估了材料强度，而且6棱锥破坏面上的6条棱边给塑性势计算带来了不便，因此出现了破坏面光滑，能考虑中间主应力影响的Drucker–Prager(D-P)^[6]，Lade-Duncan(L-D)^[7]和Matsuoka-Nakai(M-N)^[8]等准则。强度准则的合理性需通过材料试验来检验，材料在真三轴应力状态下的破坏组合对检验强度准则尤为重要。检验时通常可以在子午面和偏平面上分别比较理论预测值和实验值之间的符合程度，也可以在二维主应力σ₁-σ₂面中比较，其中后者非常便于了解中间主应力σ₂对材料屈服时的最大主应力σ₁的影响。然而对大多数强度准则而言，很难得到主应力σ₁-σ₂之间的解析关系，两者的关系通常需要多次采用数值法求解强度准则方程得到。本文作者引用等效M-C摩擦角φ_mc概念^[9-10]提出一种获得强度准则在σ₁-σ₂平面图像的简便方法，既可用于摩擦和凝聚型材料，还可用于各向异性材料。首先给出M-C的各种表示形式和相应的φ_mc定义，然后结合M-N，L-D和Moji准则作为算例演示该方法的应用。

1  Mohr-Coulomb强度准则

Coulomb强度准则认为材料破坏面上的剪应力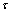和正应力σ_n之间满足如下关系：

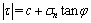               (1)

其中，参数和分别表示材料内聚力和摩擦角。

Mohr强度准则认为材料破坏面上的正应力σ_n和剪应力τ满足

|τ|=f(σ_n)                  (2)

其中，破坏函数f(σ_n)的具体形式由试验确定，且破坏发生时Mohr圆正好与破坏包络线相切。式(2)的线性形式则和式(1)等效，因此，式(1)对应的破坏准则被称为Mohr-Coulomb(M-C)强度准则。

若规定以拉应力为正，式(1)可以表示成如下形式

τ=c-σ_ntan φ                 (3)

剪应力τ和正应力σ_n可用主应力表示成

τ=(σ₁-σ₃)cos(φ/2)               (4)

σ_n=(σ₁+σ₃)/2+(σ₁-σ₃)sin(φ/2)          (5)

代入上式后可以将M-C准则替换为主应力表示形式

          (6)

由式(6)可见：式中没有考虑中间主应力σ₂。令σ₂=σ₃=0，可以得到材料单轴拉伸强度σ_t及单轴压缩强度σ_c：

        (7)

       (8)

将式(7)和(8)代入式(6)后，可以得到M-C准则的另外2种表示形式：

    (9)

               (10)

此外，利用应力张量和偏应力张量不变量定义， M-C准则还可以表示为：

 (11)

其中，静水压力σ_m定义为σ_m=σ_ii/3，偏应力张量S_ij第二不变量J₂定义为J₂=S_ijS_ij/2，偏应力张量S_ij和应力张量σ_ij之间存在如下关系：S_ij=σ_ij-σ_iiδ_ij/3；洛德角η(-30°≤η≤30°)定义为，J₃为偏应力张量S_ij第三不变量，J₃=S_ijS_jkS_ki/3，η取-30°对应三轴拉伸状态(σ₁=σ₂＞σ₃)，取30°对应三轴压缩状态(σ₁＞σ₂=σ₃)。

若令式(11)中，可以得到M-C准则的凝聚力σ₀表达式：

              (12)

利用凝聚力σ₀定义，通过平移坐标轴可以将凝聚型材料转换成无凝聚型材料^[11]，新旧坐标系下主应力分量之间的转换关系为

 (i=1，2，3)         (13)

此时，得到M-C准则的另一表示形式：

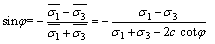    (14)

另外，利用，b(0≤b≤1)表示对中间主应力σ₂的度量^[12]，和洛德角之间满足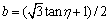，当b=0时表示三轴拉伸状态，当b=1表示三轴压缩状态，从而得到如下等式：

  (15)

        (16)

        (17)

因此，式(14)还可以表示成：

 (18)

其中，不变量之比R定义为。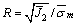

式(3), (6), (9), (11)和(18)给出了M-C准则5种表示形式，对于无凝聚力材料，c=0，由此可以得到相应的M-C摩擦角φ：

如根据式(6)，φ表示为：

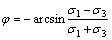              (19)

根据式(9)，φ表示为：

             (20)

根据式(11)，φ表示为：

            (21)

根据式(18)，φ表示为：

      (22)

对于大多数强度准则而言，常用σ_m，J₂，η不变量表示，因而式(21)运用更为便利。

2  等效Mohr-Coulomb摩擦角

等效M-C摩擦角φ_mc概念最先由Griffiths提出^[9]，它指所研究强度准则任一应力状态对应的M-C摩擦角。若已知所研究强度准则不同应力状态的主应力σ₁，σ₃，主应力之比σ₁/σ₃或者应力张量不变量之比R的任何一种情况，则可根据式(19)~(22)计算相应的φ_mc。利用该定义可以在统一尺度下比较各种强度准则， Griffiths利用该定义比较了用于无凝聚力材料的3种D-P准则(分别为M-C准则对应六棱锥的内切锥、外接锥和各向异性锥)，采用式(21)计算每种锥任意应力状态下(采用η或者b衡量)对应的φ_mc，只需将对应的不变量之比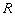代入式(21)即可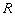，根据D-P准则不变量表达式得到。此外，Griffiths还利用式(20)比较了M-N和 L-D强度准则，任意应力状态对应的φ_mc通过求解关于σ₁/σ₃的三次函数得到。

对于凝聚力材料，即c≠0情形，Jiang等^[11]提出了一种计算φ_mc的方法：首先平移坐标轴将凝聚力材料转换为无凝聚力材料，计算无凝聚力材料的φ′_mc和主应力之比σ′₁/σ′₃，其中σ′₁/σ′₃根据式(9)得到，然后建立无凝聚力材料σ′₁/σ′₃与凝聚力材料的主应力之比σ₁/σ₃的关系：

         (23)

最后根据σ₁/σ₃得到凝聚力材料的φ_mc，即式(20)所示。

3  主应力σ₁-σ₂关系

主应力σ₁-σ₂之间的解析关系，可以由σ₂/σ₃与σ₁/σ₃关系得到，由b的定义可以得到如下关系

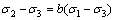            (24)

进一步表示为

             (25)

其中，σ₁/σ₃由式(23)给出，对于无凝聚材料来说，首先得到强度准则的φ′_mc，然后得到σ′₁/σ′₃，根据式(25)得到σ′₂/σ′₃；对于凝聚力材料来说，根据式(23)和得到σ₁/σ₃，然后再计算σ₂/σ₃。当σ₃已知时，从而得到σ₁-σ₂之间的关系。

4  应用算例

4.1  Matsuoka-Nakai强度准则

Matsuoka-Nakai强度准则是基于空间滑动理论提出的无黏性材料的强度准则，该准则可以看作是M-C准则的自然推广，两者表示的子午线在三轴拉伸和三轴压缩状态下重合，并且克服了M-C准则无法考虑材料中间主应力σ₂影响和屈服面存在棱边的缺点，该准则的应力张量不变量表达式为：

     (26)

式中：K_MN为取决于材料摩擦角φ的常数。

将和代入式(26)化简后得到该准则在Haigh-Westergaard坐标系统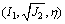下的表达式：

 (27)

求解关于的三次方程，得到的合理解为：

  (28)

其中，，称为控制偏平面图像形状参数；k₂=-k_MN/B为控制偏平面图像尺寸参数；。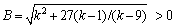

将式(28)代入式(21)或式(22)后，可以得到M-N准则在c=0情况下的φ_mc，对于c≠0情形，由式(23)可以得到相应的φ_mc。图1所示为摩擦角φ=30°时， c/σ₃=0变化到c/σ₃=+∞过程中，φ_mc和η之间的关系，可见φ_mc从三轴拉伸状态对应的-30°增加到最大值而后又减小到三轴压缩状态对应的30°，三轴拉伸和三轴压缩状态对应值相等是因为该准则和M-C准则的拉伸和压缩子午线重合。

图1  M-N准则下φ_mc和η的关系

Fig.1  Relationship between φ_mc and η under M-N criterion

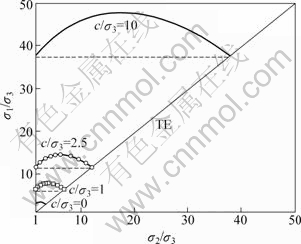
图2  M-N准则下σ₂/σ₃ 和σ₁/σ₃关系

Fig.2  Relationship between σ₂ /σ₃ and σ₁/σ₃ under M-N criterion

根据式(25)得到的σ₂/σ₃和σ₁/σ₃关系如图2所示。当c/σ₃=0时，σ₂/σ₃由1增大至3，相应的σ₁/σ₃由3增大到最大值3.55而后又减小至3，其中，三轴压缩状态(TC)对应σ₂/σ₃=1，σ₁/σ₃=3，三轴拉伸状态(TE)对应σ₂/σ₃=σ₁/σ₃=3；当c/σ₃=1，2.5和10时，具有类似的规律。另外，图2中虚线表示M-C准则σ₂/σ₃和σ₁/σ₃关系。可见：σ₂对σ₁无影响，即M-C准则不考虑中间主应力σ₂对材料屈服强度的影响。

4.2  Lade-Duncan强度准则

Lade-Duncan强度准则的应力张量不变量表达式为：

        (29)

类似于Matsuoka-Nakai强度准则，同样可以用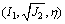表示：

  (30)

得到的合理解为

  (31)

其中，

，

。

类似于M-N准则， L-D准则在内摩擦角φ=30°时的φ_mc与η的关系如图3所示。由于L-D准则与M-C准则在三轴压缩状态(b=1, η=30°)下子午线重合，故此在η=30°时有φ_mc=30°。

图3  L-D准则下φ_mc和η的关系

Fig.3  Relationship between φ_mc and η under L-D criterion

图4所示为L-D准则的σ₂/σ₃和σ₁/σ₃关系。当c/σ₃=0时，σ₂/σ₃由1增大至3.48，相应的σ₁/σ₃由3.48增大到最大值3.92而后又减小至3，其中，三轴压缩状态(TC)对应σ₂/σ₃=1，σ₁/σ₃=3，三轴拉伸状态(TE)对应σ₂/σ₃=σ₁/σ₃=3.48；当c/σ₃=1，2.5和100时，规律    类似。

图4  L-D准则下σ₂/σ₃和σ₁/σ₃关系

Fig.4  Relationship between σ₂/σ₃ and σ₁/σ₃ under L-D criterion

4.3  Mogi强度准则

Mogi等^[13-14]发现：中间主应力σ₂确实对材料强度存在影响，并且材料的脆性断裂发生在与σ₂方向平行的平面内，因此提出的强度准则表达式如下：

(32)

若上式取线性形式，则可以表示为：

           (33)

该准则和M-C准则在三轴压缩和三轴拉伸状态重合时，可以得到系数A₁ 和 A₂的取值为：

，     (34)

式(33)在Haigh–Westergaard坐标下可表示为：

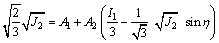     (35)

平移坐标轴后，得到不变量之比的表达式：

       (36)

图5所示为Mogi准则下内摩擦角φ=30°时的φ_mc与η的关系。不同于图1和图3的是，因该准则的偏平面图像在区间-30°≤η≤0和0≤η≤30°中对称，所以对应的φ_mc图像也关于η=0°对称。

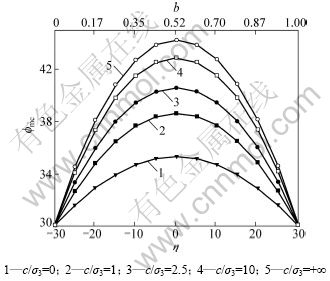
图5  Mogi准则下φ_mc和η的关系

Fig.5  Relationship between φ_mc and η under Mogi criterion

Mogi准则对应的σ₂/σ₃和σ₁/σ₃关系见图6，和前面给出的2个准则类似，σ₁先从三轴压缩状态对应的一初始值先增大到一最大值，而后又减小至三轴拉伸应力状态。由图2，4和6可知中间主应力σ₂对材料屈服强度σ₁的影响，因此3种准则均考虑了σ₂影响。

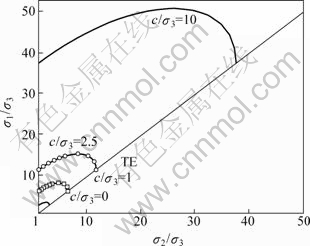
图6  Mogi准则下σ₂/σ₃ 和σ₁/σ₃关系

Fig.6  Relationship between σ₂/σ₃ and σ₁/σ₃ under Mogi criterion

5  结论

(1) 强度准则在主应力σ₁-σ₂平面上的图像可以根据该准则对应的等效M-C摩擦角得到，核心思想为先得到各应力状态对应的等效M-C摩擦角，然后基于M-C准则的主应力表达式换算出σ′₁-σ′₃，再利用中间主应力的度量b的定义得到σ′₂-σ′₃。

(2) 该方法既可用于无黏性材料又可用于黏性材料，用于黏性材料需通过平移坐标转换成无黏性材料。

(3) 给出的M-N准则，L-D准则和Moji准则算例均反映了屈服强度σ₁随中间主应力σ₂增大先增加后减小特点以及凝聚力对材料强度的影响。

参考文献：

[1] YU Mao-hong. Advances in strength theories for materials under complex stress state in the 20th Century[J]. Appl Mech Rev, 2002, 55(3): 169-218.

[2] Benz T, Schwab R. A quantitative comparison of six rock failure criteria[J]. Int J Rock Mech Min Sci, 2008, 45(7): 1176-1186.

[3] You M Q. True-triaxial strength criteria for rock[J]. Int J Rock Mech Min Sci, 2009, 46(1): 115-127.

[4] Lianyang Z, Ping C, Radha K C. Evaluation of rock strength criteria for wellbore stability analysis[J]. Int J Rock Mech Min Sci, 2010, 47(8): 1304-1316.

[5] Hosein R. New empirical polyaxial criterion for rock strength[J]. Int J Rock Mech Min Sci, 2011, 48(6): 922-931.

[6] Drucker D C. A more fundamental approach to plastic-stress strain relations[C]//Proceedings 1st U.S. National Congress on Applied Mechanics: New York: ASME, 1951: 487-491.

[7] Lade P V, Duncan J. Elasto-plastic stress-strain theory for cohesionless soil[J]. J Geotech Eng Div ASCE, 1975, 101(10): 37-53.

[8] Hajime M. Stress-strain relationships of clays based on the mobilized plane[J]. Soils and Foundations, 1974, 14(2): 77-87.

[9] Grif?ths D V. Failure criteria interpretation based on Mohr–Coulomb friction[J]. Journal of Geotechnical, 1990, 116(6): 986-999.

[10] Grif?ths D V, Huang J S. Observations on the extended Matsuoka–Nakai failure criterion[J]. Int J Numer Anal Meth Geomech, 2009, 33(17): 1889-1905.

[11] JIANG Hua, WANG Xiao-wo. A new method to calculate the equivalent Mohr–Coulomb friction angle for cohesive and frictional materials[J]. Int J Numer Anal Meth Geomech, 2011, 35(4): 630-638.

[12] Bishop A W. The strength of soils as engineering materials[J]. Géotechnique 1966, 16(2): 91-130.

[13] Mogi K. Fracture and ?ow of rocks under high triaxial compression[J]. J Geophys Res, 1971, 76(5): 1255-1269.

[14] Al-Ajmi A M, Zimmerman R W. Relationship between the parameters of the Mogi and Coulomb failure criterion[J]. Int J Rock Mech Min Sci, 2005, 42(3): 431-439.

(编辑 赵俊)

收稿日期：2011-10-10；修回日期：2011-12-30

基金项目：中国博士后科学基金资助项目(2012M510215)

通信作者：姜华(1980-)，男，江苏海门人，博士，讲师，从事结构碰撞数值模拟、材料本构模型研究；电话：13289395279；E mail：huajing@chd.edu.cn