DOI： 10.11817/j.issn.1672-7207.2019.11.019

基于球面对称设计的离散元细观参数定量确定方法

彭霞,饶秋华,李卓,张杰

（中南大学 土木工程学院，湖南 长沙，410075）

摘要:采用球面对称设计法，通过宏观参数范围确定细观参数取值范围，得到多因素球面对称设计试验表，利用试验模拟计算结果和多元回归分析，建立岩石材料颗粒流PFC2D（particle flow code 2D）的宏-细观参数关系式。采用基于宏-细观参数关系式计算得到的PFC2D细观参数，进行单轴压缩下完整岩石的应力-应变曲线和宏观力学参数、含多裂纹岩石试件断裂轨迹的模拟计算。研究结果表明：岩石的应力-应变曲线、宏观力学参数、断裂轨迹的计算结果与试验结果较吻合，从而验证了该宏-细观参数关系式的有效性；采用球面对称设计建立PFC2D宏-细观参数关系式的方法可推广应用于其他脆性材料，可为PFC定量分析复杂荷载条件下的材料细观破坏机理提供参考依据。

关键词:宏-细观参数关系式；颗粒流；球面对称设计法；平行黏结模型；岩石

中图分类号:TU45    文献标志码:A     文章编号:1672-7207（2019）11-2801-12

Quantitative determination method of mesoscopic parameters of discrete elements based on spherical symmetric design

PENG　Xia, RAO　Qiuhua, LI　Zhuo, ZHANG　Jie

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract: The spherical symmetric design method was adopted to establish the relation expression of macroscopic and mesoscopic parameters of the rock material for PFC2D（particle flow code 2D） by the spherical symmetric design table of multiple factors obtained by the value range of mesoscopic parameters based on the macroscopic parameter range and multiple regression analysis of the simulation results.Stress-strain curves and macroscopic mechanical parameters of the intact rock under uniaxial compression and the fracture trajectories of the pre-cracked rock specimen under uniaxial compression were simulated by PFC2D with calculated mesoscopic parameters using this relation expression.The results show that the simulated results of the rock stress-strain curves, macroscopic mechanical parameters and the facture trajectories are in good agreement with the experimental results, which verifies the validity of this relation expression.The establishment method of relation expression of macroscopic and mesoscopic parameters by the spherical symmetric design can be applied in other fragile materials, which provides a reliable reference for PFC to quantitatively analyze the mesoscopic failure mechanism of materials under complicated loading condition.

Key words: relation expression of macroscopic and mesoscopic parameters; particle flow code; spherical symmetric design method; parallel bonded model; rock

在深部采矿、地热开采、隧道开挖等岩体工程中，岩体内部含有的多种缺陷(如孔隙、裂纹、节理等)在长期荷载作用下会发生损伤演变，造成工程安全隐患，因此，研究岩石破坏的宏-细观机理对岩体工程的安全评定、防灾减灾等具有重大的理论指导意义。连续介质力学难以解决多裂纹扩展问题，且实验研究存在一定的局限性。目前，数值方法已成为研究岩石细观破坏机理的有效方法，其中，基于非连续性介质理论的颗粒流软件PFC(particle flow code)^[1]已广泛应用于岩土工程领域。颗粒流软件(PFC)是将材料离散成刚性颗粒后，通过模拟颗粒间的相互运动及其作用来研究真实材料的力学特性，其前提条件是选取合适的细观参数。孟京京等^[2-3]采用“试错法”标定PFC细观参数，但由于细观参数因素多且标定具有一定的盲目性与不确定性，导致标定周期长，模拟试验次数多。YOON等^[4]采用PB (Plackett-Burman)设计法测试细观参数对宏观参数(如单轴抗压强度、弹性模量、泊松比等)的敏感性，选取影响最大的2个细观参数，再通过CCD(central composite design)设计法建立宏-细观参数之间的非线性关系，可以求得细观参数，但每个宏观参数仅由较少的细观参数确定，没有考虑其他细观参数对宏观参数的影响。周喻等^[5]采用BP(back propagation)神经网络法方法，建立了宏-细观参数的非线性模型，输入宏观力学参数，即可得到岩土体细观力学参数，但BP神经网络模型的创建、学习、训练需要大量的随机组合样本。陈鹏宇等^[6]对细观参数进行正交设计，以多因素分析、量纲分析研究宏-细观参数之间的关系，确定的函数关系式只考虑单个细观参数的影响，提出了试错法标定细观参数的具体流程。目前，对于PFC细观参数的定量确定方法仍较少。为降低模拟试验次数且提高精度，需引入一种新方法来定量建立PFC宏-细观参数关系式。盛海林等^[7]提出了球面对称设计法，在球面上均匀、对称地选取试验点，通过试验建立了自变量与因变量之间的关系，该方法具有试验次数较少、精度较高等优点，更适用于多因素、多水平试验。本文采用球面对称设计法，建立PFC2D宏-细观参数定量关系式。依据材料宏观力学参数定量确定其细观参数，模拟计算单轴压缩下完整岩石试件的应力-应变曲线和宏观力学参数、含多裂纹岩石试件的断裂轨迹，并与试验结果进行对比验证，以便为PFC细观参数的定量分析提供一种有效方法。

1 球面对称设计法

在球面对称设计方法中，设因素个数为n，则球的半径r为n的平方根，球的空间维数等于n，在该球面上均匀、对称地选取试验点。考虑到任意因素对各因变量的影响均有一定范围，将这些范围以一定的代码予以统一，规定每个因素有5个水平，分别用-r，-1，0，+1和+r共5个代码表示，其中，各因素水平代码-r，0和+r对应的值分别为该因素范围的最小值、平均值、最大值；根据任意2个水平代码差的比值与该水平代码对应值差的比值相等的原则，可得到各因素水平代码-1和+1对应的值。试验次数包含3部分：所有因素的水平代码仅为-1或+1的试验次数(2ⁿ次)；1个因素水平代码为-r或+r、其余因素水平代码为0的试验次数(2n次)；各因素水平代码为0的试验次数(1次)。总试验次数为2ⁿ+2n+1次。

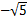以5因素为例建立球面对称设计表。设5个因素为X₁，X₂，X₃，X₄和X₅，即n=5，球半径r=，则各因素的5个水平代码为，-1，0，+1和。在设计表中，总列数为6(第1列为试验次数号)，其余每一列元素为某一因素在每次试验中的水平代码；总行数与试验总次数43(2⁵+2×5+1)相同，每行元素为5个因素的某个水平代码(5个水平代码之一)。其中，第1～32行(2ⁿ次试验)中的每一行是各因素的水平代码-1或+1的任意组合，且各行不重复；第33～42行(2n次试验)中的每一行是某一因素水平代码为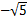或、其余因素水平代码为0的任意组合，且各行不重复；第43行为各因素水平代码为0的组合。由此可得5因素球面对称设计表，见表1。

表1　5因素球面对称设计表

Table 1　Spherical symmetric design table of five factors

2 细观参数计算公式

2.1　PFC2D建模

在PFC2D中，颗粒之间通过黏结产生相互作用，黏结模型包含接触黏结模型、平行黏结模型、平直节理接触模型3种^[8-9]。接触黏结模型中的圆形颗粒与颗粒之间为点接触，因此，不能传递力矩，当法向或切向力超过对应的黏结强度时，黏结破坏。平行黏结模型中两圆形颗粒间由平行键黏结，可以传递颗粒之间的力与力矩，该模型比接触黏结模型更接近于岩石材料真实受力情况，应用更广。平直节理接触模型是将多边形颗粒代替圆形颗粒，能够传递力与力矩，同时能抑制颗粒黏结破坏后的旋转，但需要确定更多的细观参数。

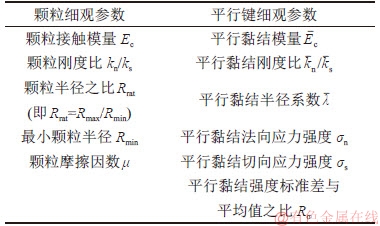
本文选取平行黏结模型，其细观参数如表2所示。为简化计算，进行以下假设^[9-11]：1) E_c=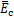； 2) 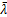=1；3) k_n/k_s=；4) R_rat=1.66。设平行黏结法向应力强度与法向应力强度之比σ_n/σ_s=m(m为比例系数)，本文取m=1^[12-13] ，故待定的独立细观参数为6个，即R_min，E_c，k_n/k_s，σ_n，μ和R_σ。

表2　PFC2D平行黏结模型中的细观参数

Table 2　Microscopic parameters of PFC2D parallel bonded model

在PCF2D建模中，先确定模型的最小颗粒半径R_min。研究结果表明^[14-15]，当R_min小到一定程度时，宏观力学参数计算结果变化不大，但R_min过小会降低数值模拟计算效率。为得到合适的R_min，以岩石单轴压缩试验为例说明。采用长为100 mm、宽为50 mm的长方形标准试样，选取4种不同的R_min(0.1，0.2，0.3和0.4 mm)进行建模，如图1所示。设其他细观参数为：E_c =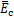=15 GPa，σ_n=σ_s=60 MPa，k_n/k_s==1.8，μ=0.5，R_σ=0.25，模拟计算不同R_min下的岩石宏观力学参数。由表3可见计算得到的弹性模量E、泊松比v、单轴抗压强度σ_c均在岩石的宏观力学参数范围内^[16]，E=10～70 GPa，v=0.15～0.30，σ_c=50～200 MPa，表明所选取的细观参数是合理可行的；当R_min减少至0.1 mm时，E，v和σ_c的计算结果与R_min=0.2时所得结果变化不大，但当R_min=0.2 mm时，所需生成的颗粒数目比R_min=0.1 mm时大大减少，因而，选定R_min= 0.2 mm。待定的独立细观参数只有5个：E_c，k_n/k_s，σ_n，μ和R_σ。

图1　单轴压缩下岩石试件PFC2D模型(R_min=0.2 mm)

Fig. 1　PFC2D model of rock specimen under uniaxial compression (R_min=0.2 mm)

表3　不同R_min下岩石宏观力学参数的模拟结果

Table 3　Simulation results of macroscopic mechanical parameters of rock with different R_min

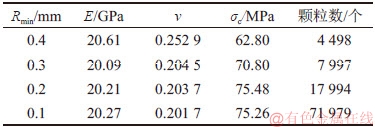
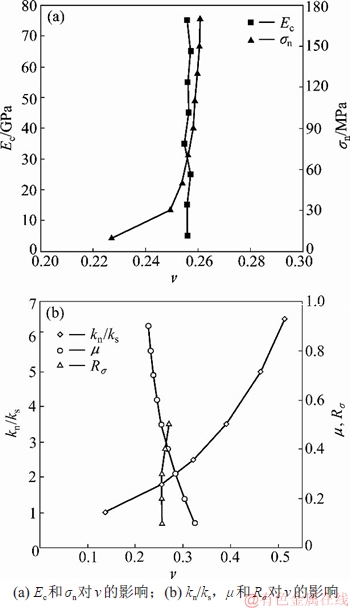
图2　细观参数对v的影响

Fig. 2　Effect of mesoscopic parameters on v

2.2　细观参数范围确定

利用球面对称设计法确定PFC2D细观参数时，首先需根据宏观参数的范围确定细观参数的取值范围。对于岩石材料，其宏观力学参数范围^[16]为：弹性模量E=10～70 GPa，泊松比v=0.15～0.30，单轴抗压强度σ_c=50～200 MPa，起裂应力与单轴抗压强度σ_ci/σ_c=0.2～0.6。在PFC2D中，σ_ci通过出现初始裂纹的应力与峰值应力的比值R设定，本文设定R为1%，即σ_ci等于当裂纹数达到峰值裂纹数的1%时所对应的应力。

采用单轴压缩试件，模型如图1所示。以初设的细观参数(E_c=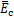=15 GPa，σ_n=σ_s=60 MPa，k_n/k_s==1.8，μ=0.5，R_σ=0.25)为基础，在改变某一个细观参数且其他4个参数不变的情况下，模拟计算单轴压缩试件的宏观力学参数，研究每个细观参数对宏观参数的影响。结果如图2～5所示。由图2可见：v基本上只与k_n/k_s有关，k_n/k_s的范围可由v的范围(0.1～0.3)确定，即k_n/k_s=1.1～2.3。由图3可见：E主要受E_c的影响，且与E_c成正比，当k_n/k_s =1.1～2.3时，对E的影响很小，可根据E的范围(10～70 GPa)确定E_c的范围，即E_c=7～51 GPa。由图4可见：σ_c与σ_n成正比，受E_c，k_n/k_s，μ和R_σ的影响较小，由此σ_n的范围可由σ_c的范围(50～200 MPa)确定，即σ_n =38～153 MPa。由图5可见：σ_ci/σ_c随着R_σ的增大而减小，随着E_c，k_n/k_s和σ_n的增大有一定波动后趋于稳定，R_σ的范围可由σ_ci/σ_c的范围(0.2～0.6)确定，即R_σ=0.13～0.27。摩擦因数μ对宏观力学参数E，v，σ_c和σ_ci/σ_c基本没有影响，只影响峰值后的响应^[9]，取μ=0.1～0.9。

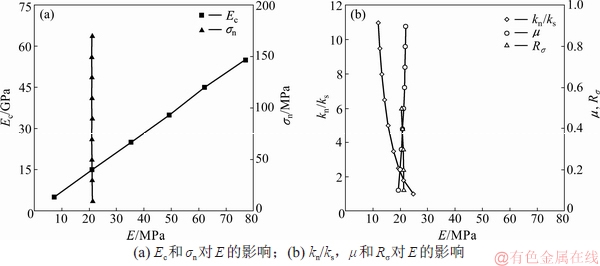
图3　细观参数对E的影响

Fig. 3　Effect of mesoscopic parameters on E

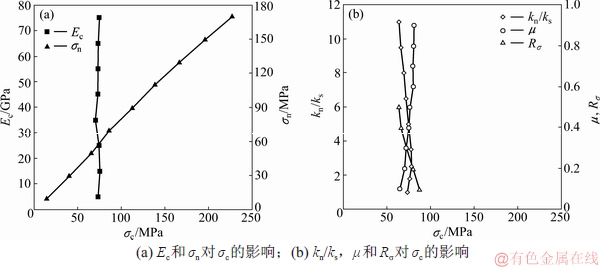
图4　细观参数对σ_c的影响

Fig. 4　Effect of mesoscopic parameters on σ_c

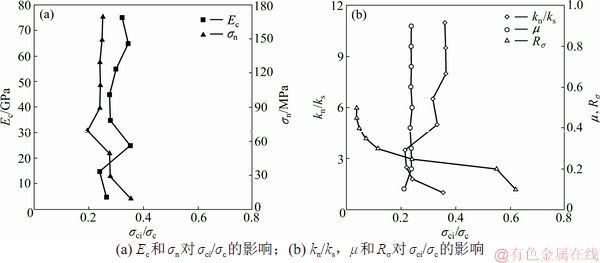
图5　细观参数对σ_ci/σ_c的影响

Fig. 5　Effect of mesoscopic parameters on σ_ci/σ_c

2.3　宏-细观参数关系式

考虑到待定的细观参数有5个，采用5因素球面对称设计表(表1)，5因素X₁，X₂，X₃，X₄和X₅分别为E_c，k_n/k_s，σ_n，μ和R_σ。为确定表1中各因素水平代码对应的值，以因素E_c为例说明，E_c的范围为7～51，则E_c的水平代码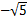，0和所对应的值分别为7，29和51。令X₁的水平代码-1和1对应的值分别为x和y(表4)，根据上述比值相等的原则，有

解得x=19.16，y=38.84。同理，可求得其他因素水平代码对应的值，如表5所示。将表5中各因素水平代码对应的值与表1中的值相对照，可得到具体的球面对称设计试验表，如表6所示。

根据球面对称设计试验表(表6)，选取每行中的5个细观参数值，进行PFC2D模拟计算。表7所示为模拟计算43次试验得到的岩石单轴压缩试件宏观力学参数(E，v，σ_c和σ_ci/σ_c)，参数范围为：E=10.16～72.77 GPa，v=0.1603～0.315，σ_c=49.70～198.98 GPa，σ_ci/σ_c=0.244～0.674，基本符合岩石的力学参数范围。

表4　因素E_c水平代码对应的值

Table 4　Corresponding values for horizontal codes of factor E_c

表5　各因素水平代码对应的值

Table 5　Corresponding values for horizontal codes of each factor

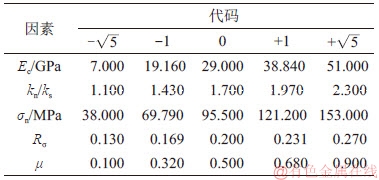
表6　球面对称设计试验表

Table 6　Spherical symmetric design table

表7　球面对称设计试验模拟结果

Table 7　Simulation results of spherical symmetry design test

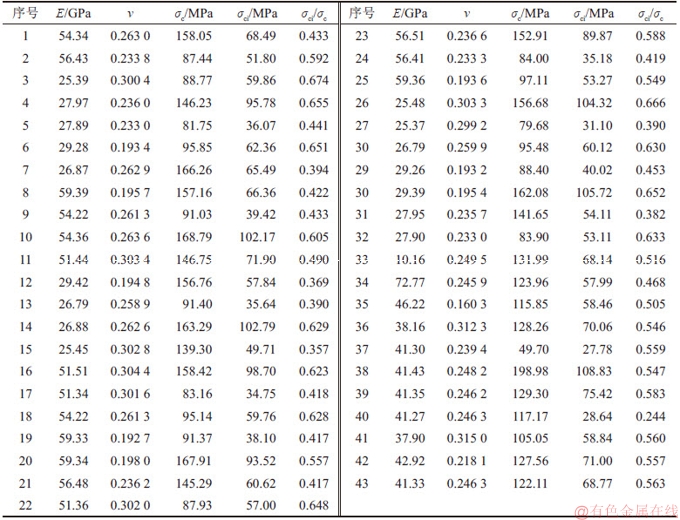
球面对称设计的试验结果可采用线性或非线性方法拟合^[7]，本文采用多元线性回归对表7中模拟试验结果进行拟合，分别建立4个宏观参数(E，v，σ_c和σ_ci)与5个细观参数(E_c，k_n/k_s，σ_n，μ和R_σ)之间的关系式：

(1)

相关系数R²均在90%以上，表明拟合精度较高，能够准确反映岩石宏-细观参数的关联性，其中摩擦因数主要影响峰值后的响应，建议取μ=0.5^[9]。式(1)适用于宏观力学参数满足E=10～70 GPa，v=0.15～0.30，σ_c=50～200 MPa，σ_ci/σ_c=0.2～0.6的岩石材料。 若已知岩石4个宏观参数(E，v，σ_c和σ_ci)，由式(1)可计算得到4个细观参数。

3 实验验证

3.1　岩石单轴压缩实验

为验证宏-细观参数关系式(1)，选取7种不同的岩石材料，根据其宏观力学参数(见表8)，分别计算得到PFC2D细观参数值(E_c，k_n/k_s，σ_n和R_σ)，如表9所示。

表8　不同岩石的宏观力学参数(试验结果)

Table 8　Macroscopic mechanical parameters of different rocks (experimental results)

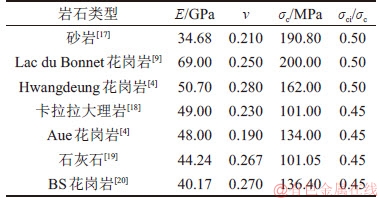
表9　不同岩石的PFC2D细观参数(计算结果)

Table 9　PFC2D microscopic parameters of different rocks (calculated results)

基于不同岩石材料的PFC2D细观参数(表9)，采用标准岩石试样(长×宽为50 mm×100 mm)进行单轴压缩模拟计算，得到应力-应变曲线(见图6，以砂岩和BS花岗岩为例)和宏观力学参数(见表10)，并与试验结果进行对比。由图6可见：模拟应力-应变模拟曲线可分为弹性、损伤和破坏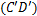3个阶段，但没有出现类似试验曲线(OABCD)的压密过程(OA)，这是由于在压缩试验的初始阶段，微孔、微裂缝等闭合引起非线性不可逆变形(OE)。计算得到的砂岩弹性模量E段斜率)和压缩强度σ_c(峰值点应力)分别为34.17 GPa和193.53 MPa，与实测值E=34.68 GPa，σ_c=190.8 MPa相比相对误差均较小，均约为2%；同理，计算得到的BS花岗岩E和σ_c与实测值相对误差均小于2%。当忽略压密阶段、试验曲线ABCD向原点水平左移OE段后，所得曲线与模拟曲线基本重合，两者吻合较好。

不同岩石试样在单轴压缩下宏观力学参数的模拟结果与试验结果对比见表10。从表10可见：两者相对误差小于5%，精度较高，表明采用球面对称设计建立的宏-细观关系式(1)计算PFC2D细观参数的方法是合理的、有效的。

表10　不同岩石的宏观力学参数(模拟与试验结果对比)

Table 10　Macroscopic mechanical parameters of different rocks (comparison of simulation and test results)

3.2　岩石多裂纹断裂试验

为进一步验证宏-细观参数关系式(1)，模拟含3条平行裂纹的砂岩试件(长160 mm、宽80 mm、厚30 mm)的单轴压缩断裂试验^[17]。如图7所示，试件模型中从上至下依次为预制裂纹1、预制裂纹2、预制裂纹3，预制裂纹长为15 mm，宽为2.5 mm，预制裂纹1与预制裂纹2和3内尖端的距离2b=20 mm，垂直于预制裂纹2和3的距离d=10 mm，预制裂纹1的水平夹角α=45°，预制裂纹1和3内尖端连线与水平方向的夹角β=75°，实测的砂岩宏观力学参数和基于关系式(1)计算得到的PFC2D细观参数见表8和表9。

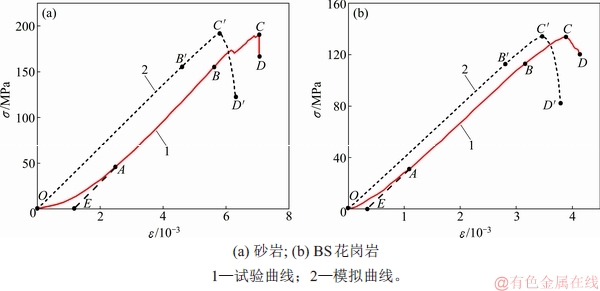
图6　单轴压缩下完整岩石的应力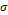-应变曲线

Fig. 6　Stress-strain curves of intact rocks under uniaxial compression

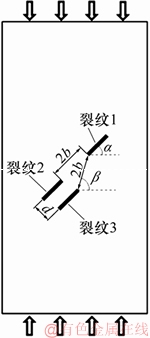
图7　含3条平行裂纹砂岩试件模型

Fig. 7　Model of sandstone specimen with three parallel cracks

在单轴压缩下，含3条平行裂纹的砂岩试件裂纹扩展轨迹其PFC2D模拟结果和试验结果分别如图8和图9所示。由模拟结果可知：3条平行裂纹AB，CD和EF均有新裂纹分别从裂尖起裂(图8(a))，沿着轴向加载方向扩展(与含单一斜裂纹的试件扩展形式相同)，其中，浅色和深色分别表示拉应力和剪应力超过平行键法向强度、剪切强度而形成的拉裂纹、剪裂纹，拉裂纹居多，起裂主要受拉应力控制。从图9(a)可见：只有2条平行裂纹AB和CD的尖端先出现新裂纹，这可能是实际岩石材料的非均质性所致。从图8(b)可见；随着荷载增加，裂尖E的新裂纹因到裂纹AB和CD的距离较远，相互影响较小，仍沿原轴向加载方向扩展，而裂尖F的新裂纹逐渐扩展至裂尖C附近区域，最终与裂尖C贯通；裂尖B和裂纹C扩展因受到裂尖D和A的应力强度因子影响而改变方向，最终与裂尖D和A贯通尖端；裂尖A和D新裂纹沿轴向加载方向双向扩展，裂尖A和D逐渐贯通，与图9(b)所示实验结果相符，此时，裂尖A，C和D均有2条裂纹相互贯通，应力集中得到释放，裂尖B只有1条新裂纹，故产生次生裂纹(图8(c)，9(c))。从图8(d)和图9(d)可见：随着进一步加载，裂尖E的新裂纹逐步向试件上端扩展时受到压密阻碍，又分叉衍生出向下扩展的次生裂纹。但模拟中次生裂纹趋向于与试件右侧边缘贯通，试验中次生裂纹轴向加载方向延伸，其中差异可能是实际岩石材料的非均质性所致。由此可见：在单轴压缩下，含3条平行裂纹的砂岩试件裂纹扩展轨迹其PFC2D模拟结果与试验结果较吻合，从而验证了采用球面对称设计法标定PFC2D细观参数的合理性和可靠性。

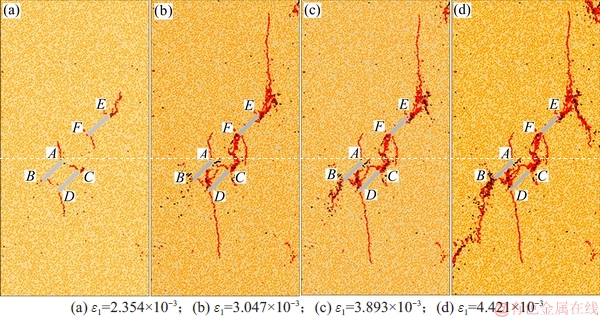
图8　单轴压缩下含3条平行裂纹的砂岩试件裂纹扩展轨迹(模拟结果)

Fig. 8　Propagation trajectories of sandstone specimen with three parallel cracks under uniaxial compression(simulation results)

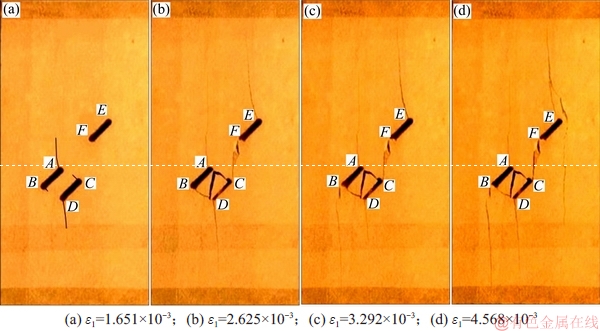
图9　单轴压缩下含3条平行裂纹的砂岩试件裂纹扩展轨迹(试验结果)^[17]

Fig. 9　Propagation trajectories of sandstone specimen with three parallel cracks under uniaxial compression(test results)

4 结论

1) 采用球面对称设计法，通过宏观参数范围确定细观参数取值范围，得到多因素球面对称设计试验表，利用试验模拟计算结果和多元回归分析，建立了PFC2D宏-细观参数关系式。

2) 采用基于宏-细观参数关系式计算得到的PFC2D细观参数，模拟计算单轴压缩下完整岩石的应力-应变曲线和宏观力学参数、含多裂纹岩石试件断裂轨迹，计算结果与试验结果较吻合，从而验证了该宏-细观参数关系式的合理性和可行性。

3) 采用球面对称设计建立PFC2D宏-细观参数关系式的方法可推广应用于其他脆性材料，为PFC定量分析复杂荷载条件下的材料细观破坏机理提供参考。

参考文献：

[1] Itasca Consulting Group Inc. The manuals of particle flow code in 2 dimension. Version 3.0[M]. Minneapolis: Mill Place, 2002: 36-49.

[2] 孟京京, 曹平, 张科, 等. 基于颗粒流的平台圆盘巴西劈裂和岩石抗拉强度[J]. 中南大学学报(自然科学版), 2013, 44(6): 2449-2454.

MENG Jingjing, CAO Ping, ZHANG Ke, et al. Brazil split test of flattened disk and rock tensile strength using particle flow code[J]. Journal of Central South University (Science and Technology), 2013, 44(6): 2449-2454.

[3] 杨庆, 刘元俊. 岩石类材料裂纹扩展贯通的颗粒流模拟[J]. 岩石力学与工程学报, 2012, 31(S1): 3123-3129.

YANG Qing, LIU Yuanjun. Simulations of crack propagation in rock-like materials using particle flow code[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 3123-3129.

[4] YOON J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 871-889.

[5] 周喻, 吴顺川, 焦建津, 等. 基于BP神经网络的岩土体细观力学参数研究[J]. 岩土力学, 2011, 32(12): 3821-3826.

ZHOU Yu, WU Shunchuan, JIAO Jianjin, et al. Research on mesomeechanical parameters of rock and soil mass based on BP neural network[J]. Rock and Soil Mechanics, 2011, 32(12): 3821-3826.

[6] 陈鹏宇, 孔莹, 余宏明. 岩石单轴压缩PFC^2D模型细观参数标定研究[J]. 地下空间与工程学报, 2018, 14(5): 1240-1249.

CHEN Pengyu, KONG Ying, YU Hongming. Research on the calibration method of microparameters of a uniaxial compression PFC2D model for rock[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(5): 1240-1249.

[7] 盛海林, 涂家生. 球面对称设计在药剂学上的应用[J]. 中国药科大学学报, 1996, 27(4): 211-214.

SHENG Hailin, TU Jiasheng. Application of spherical symmetric design in pharmaceutics[J]. Journal of China Pharmaceutical University, 1996, 27(4): 211-214.

[8] CHEN Pengyu. Effects of microparameters on macroparameters of flat-jointed bonded-particle materials and suggestions on trial-and-error method[J]. Geotechnical and Geological Engineering, 2017, 35(2): 663-677.

[9] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364.

[10] HUANG H. Discrete element modeling of tool-rock interaction[D]. Minneapolis, USA: University of Minnesota, 1999: 17-24.

[11] YANG B, JIAO Y, LEI S. A study on the effects of microparameters on macroproperties for specimens created by bonded particles[J]. Engineering Computations, 2006, 23(6): 607-631.

[12] 徐金明, 谢芝蕾, 贾海涛. 石灰岩细观力学特性的颗粒流模拟[J]. 岩土力学, 2010, 31(S2): 390-395.

XU Jinming, XIE Zhilei, JIA Haitao. Simulation of mesomeechanical properties of limestone using particle flow code[J]. Rock and Soil Mechanics, 2010, 31(S2): 390-395.

[13] 方前程, 周科平, 刘学服. 不同围压下断续节理岩体破坏机制的颗粒流分析[J]. 中南大学学报(自然科学版), 2014, 45(10): 3536-3543.

FANG Qiancheng, ZHOU Keping, LIU Xuefu. Failure mechanism of discontinuous joint rock mass under different confining pressures based on particle flow code[J]. Journal of Central South University(Science and Technology), 2014, 45(10): 3536-3543.

[14] CUNDALL P A. Formulation of a three-dimensional distinct element model: Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1988, 25(3): 107-116.

[15] ALEFELD G,MAYER G. Interval analysis: theory and applications[J]. Journal of Computational and Applied Mathematics, 2000, 121(1/2): 421-464.

[16] 水利水电科学研究院, 水利水电规划设计总院, 水利电力情报研究所, 等. 岩石力学参数手册[M]. 北京: 水利水电出版社, 1991: 135-138.

Institute of Water Resources and Hydropower Research,General Institute of Water Resources and Hydropower Planning and Design, Institute of Water Conservancy and Electric Power Information, et al. The manual of rock mechanics parameters[M]. Beijing: China Water Power Press, 1991: 135-138.

[17] YANG S Q, YANG D S, JING H W, et al. An experimental study of the fracture coalescence behaviour of brittle sandstone specimens containing three fissures[J]. Rock Mechanics and Rock Engineering, 2012, 45(4): 563-582.

[18] ALBER M, HAUPTFLEISCH U. Generation and visualization of microfractures in Carrara marble for estimating fracture toughness, fracture shear and fracture normal stiffness[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(8): 1065-1071.

[19] ALBER M, HEILAND J. Investigation of a limestone pillar failure part 2: stress history and application of fracture mechanics approach[J]. Rock Mechanics and Rock Engineering, 2001, 34(3): 187-199.

[20] DUAN K, KWOK C Y, THAM L G. Micromechanical analysis of the failure process of brittle rock[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(6): 618-634.

（编辑 陈灿华）

收稿日期： 2019 -01 -21; 修回日期： 2019 -04 -23

基金项目(Foundation item)：国家自然科学基金资助项目(51474251, 51874351)(Projects(51474251, 51874351) supported by the National Natural Science Foundation of China)

通信作者：饶秋华，博士，教授，从事断裂与损伤力学研究；E-mail: raoqh@csu.edu.cn