Trans. Nonferrous Met. Soc. China 24(2014) 3994-4003

Arrhenius parameters determination in non-isothermal conditions for mechanically activated Ag₂O-graphite mixture

Seyed Hadi SHAHCHERAGHI¹, Gholam Reza KHAYATI²

1. Department of Mineral Processing Engineering, Shahid Bahonar University of Kerman, Kerman, Iran;

2. Department of Materials Science and Engineering, Shahid Bahonar University of Kerman, Kerman, Iran

Received 25 February 2014; accepted 23 June 2014

Abstract: The non-isothermal kinetics of mechanochemical reduction of Ag₂O with graphite was studied by DSC and TGA with a model of fitting Malek approach and a model-free advanced isoconversional method of Vyazovkin. To evaluate the kinetics parameters, Ag₂O–graphite mixture of as-received and milled for 2 and 4 h samples were selected. Based on the results obtained by Vyazovkin method calculation, however, the difference between the maximum and minimum values of activation energy is less than 20%-30% of the average activation energy ((99.38±2.36) kJ/mol) and thermal decomposition of mechanically activated Ag₂O for 2 h is a multi-step process. Moreover, the thermal decomposition of mechanically activated Ag₂O–graphite powder activated for 4 h is a single-step process (the average activation energy=(93.68±2.26) kJ/mol). The kinetics modeling shows that the complexity of thermal decomposition of as-received Ag₂O-graphite mixture is higher than that of the others. While, the autocatalytic tendency of as-received Ag₂O–graphite mixture is lower than that of the others.

Key words: mechanical activation; Vyazovkin method; kinetic modeling; Sestak–Berggren model; integral master plot method; silver oxide

1 Introduction

Ag₂O is one of thermodynamically stable silver oxides. Firstly, the decomposition kinetics of Ag₂O was studied by L’VOV [1] in 1905, who paid attention to reaction autocatalytic characters. These specific features of the reaction were later confirmed by other authors [2-6]. The temperatures varied in these studies from about 173 to 399 °C, and the activation energies, in the 118-180 kJ/mol interval [2-6]. The results showed that the thermal decomposition kinetics of Ag₂O occurred using the scheme of dissociative evaporation of Ag₂O in the form of free Ag atoms and O₂ molecules with simultaneous condensation of Ag vapor [1].

The authors previously studied the kinetics of mechanochemical decomposition of silver oxide with graphite in isothermal conditions [7-10]. The results showed that the mechanisms of nuclei growth in thermal and mechanochemical reduction were diffusion controlled and interface controlled, respectively.

In our previous work, the non-isothermal kinetics of thermal decomposition of Ag₂O-graphite mixture was systematically investigated by a differential scanning calorimeter (DSC) in terms of a model-fitting Malek approach, integral master plot method and a model-free advanced isoconversional method of Vyazovkin [11]. The results showed that the decomposition of as-received Ag₂O–graphite mixture (not activated) consisted of two steps [11]. The first step of decomposition of as-received Ag₂O–graphite mixture was a complex process with the participation of at least two mechanisms and the second step was a single-step process (the average activation energy=(118.93±3.95) kJ/mol) [11]. Furthermore, the first step of the Ag₂O thermal decomposition process in the range of 0.10≤conversion degree≤0.55 was followed an autocatalytic model, and in the range of 0.552O thermal decomposition process followed an autocatalytic model [11].

To the best of our knowledge, there is not a great deal of information in the literature about the effect of mechanical activation on non-isothermal decomposition kinetics of Ag₂O–graphite mixture. In this work, the effects of mechanical activation for 0, 2 and 4 h using high energy planetary ball mill on thermal decomposition kinetics of Ag₂O–graphite powder mixture were studied. The results showed that the thermal decomposition of Ag₂O occurred as an endothermic reaction due to the insufficient activation of graphite.

In this work, the effect of mechanical activation was investigated on thermal decomposition of Ag₂O–graphite mixture. To study the effect of mechanical activation on non-isothermal decomposition kinetics of Ag₂O– graphite mixture, the activation energies of as-received and mechanically activated for 2 and 4 h samples were calculated as a function of conversion degree of Ag₂O decomposition and compared with each other. Moreover, the kinetics of decomposition of as-received and mechanically activated for 2 and 4 h samples were investigated by model-fitting Malek approach, integral master plot approach and a model-free advanced isoconversional approach of Vyazovkin in a systematic and comparative way. Our current contribution will provide the comprehensive data to better understand the mechanism of dissociation.

2 Experimental

Starting materials were commercially Ag₂O powder (99% purity, 5-40 μm, Merck) and graphite (99.9%, 10–50 μm). The mechanical activation of Ag₂O together with 40% (mole fraction) of extra graphite as reducing agent (according to Eq. (1)) was carried out in a high energy planetary ball mill [12].

2Ag₂O(s)+xC(s)→4Ag(s)+CO₂(g)+(x-1)C, x=1.4   (1)

Details of ball milling process are given in Table 1. To evaluate the kinetics parameters, 30 mg of Ag₂O– graphite mixture of as-received and milled for 2 and 4 h samples were selected. Thermal analyses of samples were performed under flowing argon with a STA409PG device equipped with thermogravimetric (TG) system and Al₂O₃ crucible. The non-isothermal differential scanning calorimetry (DSC) analyses were carried out at the heating rates of 5, 10, 15 and 20 °C/min. The flow rate of argon was adjusted to 500 mL/min. Details of ball milling process are given in Table 1. The samples were characterized by SEM (JEOLJSM 5310) equipped with an energy dispersive spectrometer (EDS) (Oxford Instrument) and XRD (Simens-D8 Advanced) using Cu K_α radiation. The line broadening due to the instrument was calculated from Warren’s method [13]. The average crystallite size and internal strain were estimated with Scherer equation [14].

3 Theoretical

Generally, the rate of degradation reaction can be described in terms of two functions, k(T) and f(α), thus,

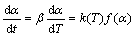                       (2)

where α is the degree of conversion (that is proportional to the area under the DSC curve); t is the reaction time; T is the thermodynamic temperature; β is the heating rate; k(T) is the rate constant; and f(α) is the type of reaction or function of reaction mechanism. The dependence of the reaction rate constant on temperature can be described by the Arrhenius equation:

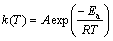                          (3)

where A is the pre-exponential factor; R is the gas constant; E_a is the apparent activation energy.

Table 1 Details of ball mill machine and milling conditions

A relatively complete thermal analysis kinetics method proposed in Refs. [11,15,16] was chosen to analyze the non-isothermal experiment data. The Malek method contains two functions, y(α) and z(α), to find the appropriate kinetic model that best describes the conversion function of the studied process. They are as follows [11,15,17]:

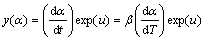            (4)

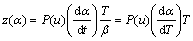              (5)

where u=E_a/(RT) and P(u) are the expression of the temperature integral, which can be well approximated by the fourth rational expression [11,15,18] as shown in Eq. (6):

           (6)

Function y(α) is proportional to function f(α), being characteristic for a given kinetic model. The shapes and maxima of both y(α) and z(α) functions, normalized within the (0, 1) interval, provide valuable information for determining the most appropriate kinetic model to describe the process studied.

According to the Malek method, E_a must be determined independently by other methods. In order to estimate the activation energy, various methods have been proposed. These methods can be generally categorized as isoconversional and model-fitting methods [19-24].

Model fitting methods depend on the reaction model and also assume the Arrhenius temperature dependent of the rate constant k(T). They do not make a clear separation between the temperature dependent k(T) and the reaction model f(α). In addition, the temperature sensitivity of the reaction rate depends on α. The best known model-fitting approaches are the Coats-Redfern (CR) method [25] and the invariant kinetic parameters (IKP) method [26].

Isoconversional methods can be generally divided into integral method and differential method. The integral method relies on the temperature integral approximation, mainly including the Kissinger–Akahira– Sunose (KAS) method [27-30] and the Flynn–Wall– Ozawa (FWO) method [22,23]. The differential method, such as the Friedman method [21,31], employs the instantaneous values of conversion degree rates, and this method is therefore sensitive to the experimental noise.

In addition, there are more complex model free methods, like the non-linear isoconversional method by VYAZOVKIN and WIGHT [32,33], solutions of which can only be obtained by computer algorithms.

Due to the great calculation accuracy and versatile applicability for various heating programs [11,34], the advanced isoconversional methods developed by VYAZOVKIN, and the VYAZOVKIN method, are adopted to analyze the non-isothermal reaction. Specifically, the Vyazovkin method is applicable to a non-isothermal kinetic process with a series of linear heating, which can be written as [11,35]

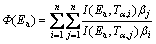                    (7)

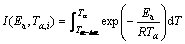               (8)

where β_i and β_j represent the different heating rates; T_α and T_α-△α are the reaction temperatures corresponding to α and α-△α, respectively. Minimizing Eq. (7) for each α with a certain conversion increment (usually △α=0.05) results in the correction of E_a with α. The detailed descriptions to use the Vyazovkin method to treat calorimetric data can be acquired elsewhere [11,36,37].

4 Results and discussion

4.1 Non-isothermal decomposition of Ag₂O–graphite mixture

The TG-DSC curves of non-isothermal degradation of Ag₂O–graphite mixture of as-received and milled for 2 and 4 h samples at four different heating rates (5, 10, 15 and 20 °C/min) are shown in Figs. 1-3. According Fig. 1, the thermal decomposition of the Ag₂O powder occurred in two steps.

Fig. 1 TG-DSC curves for thermal decomposition of as-received Ag₂O–graphite mixture at different heating rates [11] (30 mg mixture of Ag₂O powder (99% purity, 5-40 μm, Merck) and graphite (99.9% purity, 10-50 μm) and flow rate of argon of 500 mL/min)

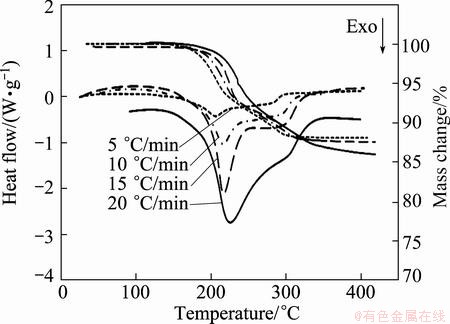
Fig. 2 TG-DSC curves for thermal decomposition of mechanically activated Ag₂O–graphite mixture for 2 h at different heating rates (30 mg mixture of Ag₂O powder (99% purity, 5-40 μm, Merck) and graphite (99.9% purity, 10-50 μm) and flow rate of argon of 500 mL/min

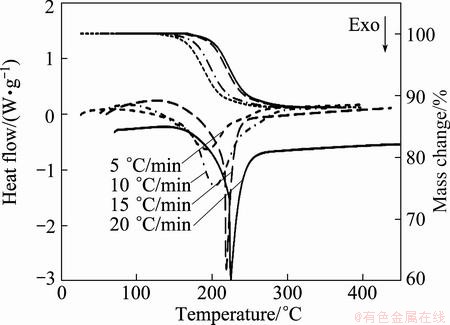
Fig. 3 TG-DSC curves for thermal decomposition of mechanically activated Ag₂O–graphite mixture for 4 h at different heating rates (30 mg mixture of Ag₂O powder (99% purity, 5-40 μm, Merck) and graphite (99.9% purity, 10-50 μm) and flow rate of argon of 500 mL/min

First, peak occurring at 197-217 °C can be attributed to the porous Ag₂O powder decomposition to porous silver particles as follows [10,11,38]:

Ag₂O(s)→2Ag(s)+1/2O₂(g)                    (9)

The shoulder at the end of the first peak (for all heating rates) probably can be attributed to the formation of aggregates of silver atoms in oxide lattice [6,11]. Second, peak occurring at 362-400 °C, can be attributed to a structure change from porous particles to the silver bulk crystals [11,39]. As shown in Figs. 2 and 3, the mechanochemical decompositions of samples milled for 2 and 4 h were characterized by exothermic peak in the DSC curves, respectively.

Accordingly, the mechanical activation shifts the reaction temperature in the range of 140-436 °C (for as-received sample) to 170-335 °C and 161-250 °C after 2 and 4 h milling, respectively (Figs. 1-3, Table 2). It can be seen from Figs. 1-3, with increasing heating rate, the reaction area was shifted to a higher temperature range. Moreover, onset reaction temperatures, peak temperatures, and end temperatures enhanced with increasing heating rate, and decreased with increasing milling time (see Table 2). From DSC curves the temperatures of the peaks (T_Peak) of degradation can be determined. The onset temperatures (T_onset) and the end temperatures (T_end) of degradation can then be calculated from the TG curves.

As known, mechanical activation introduces many vacancies, lattice defects, grain boundaries and surfaces [40-42], which leads to the decrease in decomposition temperature of Ag₂O–graphite mixture. In addition, for mechanically activated sample for 2 h, the shoulder peak at higher temperatures could be probably related to the thermal decomposition of Ag₂O occurring as a parallel reaction (Eq. (8)) at higher temperatures.

Table 2 Typical parameters of thermal decomposition of as-received sample and mechanically activated Ag₂O–graphite powder for 2 and 4 h

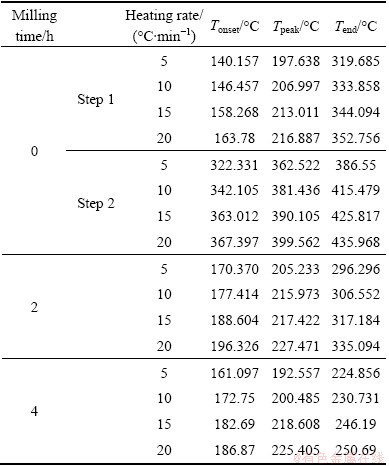
The conversional curves (α-T) for non-isothermal decomposition of samples milled for 2 and 4 h are shown in Fig. 4. These conversional curves exhibit the sigmoid profile, and by increasing heating rate, the curves shift towards the higher temperature. In other words, the higher the heating rate, the higher the temperature for the reaction to reach the identical α. Also, with increasing the milling time, the conversional curve was shifted to a lower temperature range at an identical heating rate.

4.2 Calculation of activation energy (E_a)

The dependence of E_a on α for decomposition of as-received Ag₂O–graphite mixture and samples milled for 2 and 4 h, is presented in Fig. 5. As mentioned previously, mechanical activation decreased the activation energy of decomposition [40,41]. Furthermore, mechanical milling led to an increase in contact areas between the particles [42]. Taking all these factors into account leads to a decrease in the decomposition temperature of Ag₂O–graphite mixture (see Figs. 1-3).

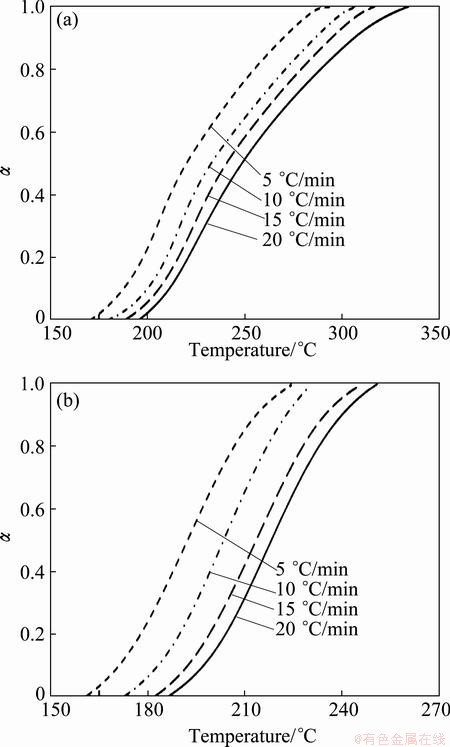
Fig. 4 α-T curves for Ag₂O–graphite mixture samples milled for 2 h (a) and 4 h (b)

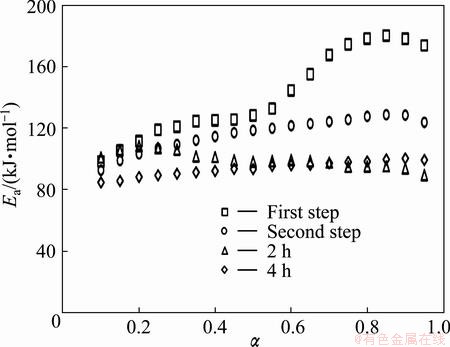
Fig. 5 Dependence of activation energy (E_a) on conversion (α) for decomposition of as-received sample and mechanically activated Ag₂O–graphite powders for 2 and 4 h

It could be pointed out that if E_a values are independent of α, the decomposition process is dominated by a single reaction step [43,44]. On the contrary, a significant variation of E_a with α should be interpreted in terms of the multi-step mechanism [43-46]. Therefore, from Fig. 5, it was obvious that the first step of Ag₂O–graphite mixture decomposition was a complex process with the participation of at least two mechanisms [11]. It could be considered that the E_a values are independent of α if the difference between the maximum and minimum values of E_a was less than 20%-30% of the average E_a [11,35,47]. Therefore, the dependence of E_a on α, according to Vyazovkin method, for the first step could be divided into two different regions (α≤0.55 and α>0.55). In the first region (α≤0.55), in the range of 0.1≤α <0.25, there is a linear increase of E_a with α, while in the range of 0.25≤α≤0.55, E_a presents an almost stable behavior. In the second region (α>0.55), in the range of 0.55<α<0.70, there is linear increase of E_a with α, while in the range of 0.75≤α≤0.95, E_a presents an almost stable behavior. The first and second regions of the first step of Ag₂O powder decomposition could be attributed to the porous Ag₂O decomposition to porous silver particles and the formation of aggregates of silver atoms, respectively [6,11].

Based on the obtained results by the Vyazovkin method, the average values of E_a for the first step of Ag₂O–graphite mixture decomposition in the range of 0.10≤α<0.55 and 0.55<α≤0.95 were (118.953±3.429) and (168.871±4.518) kJ/mol, respectively [11]. In the second step, in the range of 0.10≤α≤0.90, there is an almost linear increase of E_a with α. As shown in Fig. 5, it was obvious that the difference between the maximum and minimum values of E_a was less than 20%-30% of the average E_a (118.933±1.975 kJ/mol) [11]. Therefore, E_a presents an almost stable behavior and the second step of Ag₂O–graphite mixture decomposition is a single-step process.

Furthermore, the variation of E_a for α<0.10 and α>0.90 was not of major concern, because the parameters were affected hardly by the startup of the experiment and minor errors in baseline determination, respectively [35]. The activation energy of sample milled for 2 h at α<0.20 was dramatically increased while for α between 0.20 and 0.50 had a decreasing rate. The same trend was observed for α>0.50. This behavior could be related to the formation of Ag layer (due to the progress of α) and detachment of Ag layer (due to the increase in lattice strain within the interface) at the Ag₂O-graphite interface. Therefore, thermal decomposition of Ag₂O mechanically activated for 2 h was a multi-step process.

As shown in Fig. 5, the activation energy of sample milled for 4 h, tends to increase slightly (the average E_a=(93.679±1.131) kJ/mol). This could be attributed to the agglomeration of fine particles during intensive milling and therefore to the formation of a dense layer as a result of the partial sintering at higher temperatures. As a result, the effect of disordering of Ag₂O structure overlapped by the formation of a dense layer. Consequently, the reduction was retarded [48-50]. On the other hand, the graphite was activated as a reducing agent in the conversion range of 0.10≤α≤0.95 and consequently, Ag₂O reduced to Ag according to Eq. (1). Therefore, the mechanochemical reduction of sample milled for 4 h was a single-step process and could be described by an autocatalytic model. Moreover, with increasing milling time to 4 h, the average particle size of precursor was reduced and decomposition reaction of Ag₂O was completed by the formation of Ag layer at the Ag₂O-graphite interface. In this case, the change of E_a as a function of α was neglected.

It should be mentioned that the dependence of E_a on α was a source of additional kinetic information of process [51-54]. The results indicated that the dependence of E_a on α helped not only to reveal the complexity of reduction processes, but also to identify its kinetic scheme. Therefore, we determined the suitable kinetics models for the effect of practical parameter of milling such as milling time and mechanical activation on the decomposition of Ag₂O.

The relationship between the reaction rate and conversion of decomposition of as-received sample and mechanically activated Ag₂O–graphite powders for 2 and 4 h showed that, for all samples, the reaction rate (βdα/dT) increases with the heating rate. Furthermore, the peak reaction rate appears at the conversion degree (α_p) range of 0.253-0.325 and 0.491-0.526 for mechanically activated Ag₂O–graphite powders for 2 and 4 h, respectively. Hence, the model-free kinetic method is suitable for the experiment. This observation likely implies that the mechanical activation greatly affects the reaction kinetics, but hardly affects the basic reaction mechanisms.

The normalized function curves of y(α) and z(α) were constructed by following Eq. (4) and Eq. (5) for as-received Ag₂O-graphite mixture and mechanically activated Ag₂O–graphite powder for 2 and 4 h (see Fig. 6). Figure 6 clearly indicates that the y(α) curves exhibit peak values at conversion degree α_M between 0.102 and 0.104, and the z(α) curves show a practically isoconversional peak conversion degree, α_p^∞, within 0.303-0.330 for mechanically activated Ag₂O–graphite powder for 2 h.

Table 3 shows the characteristic peak conversion degrees, α_p, α_M and α_p^∞, for decomposition of as-received Ag₂O-graphite mixture and mechanically activated Ag₂O–graphite powders for 2 and 4 h. This finding demonstrates that the effect of the heating rates on the whole reaction kinetics can be omitted by applying the Malek method to the non-isothermal kinetics data of Ag₂O degradation. Furthermore, the peak value of y(α) appears while α is much higher than 0, implying that the reaction is auto-catalyzed [55]. Besides, the higher value of α_M indicates the increasing autocatalytic tendency of the degradation process [55]. As shown in Table 3, autocatalytic tendency of the degradation process of mechanically activated Ag₂O–graphite powder for 4 h is more than Ag₂O–graphite powder mechanically activated for 2 h and as-received sample (the first step), respectively (α_M^4h>α_M^2h>α_M^0h).

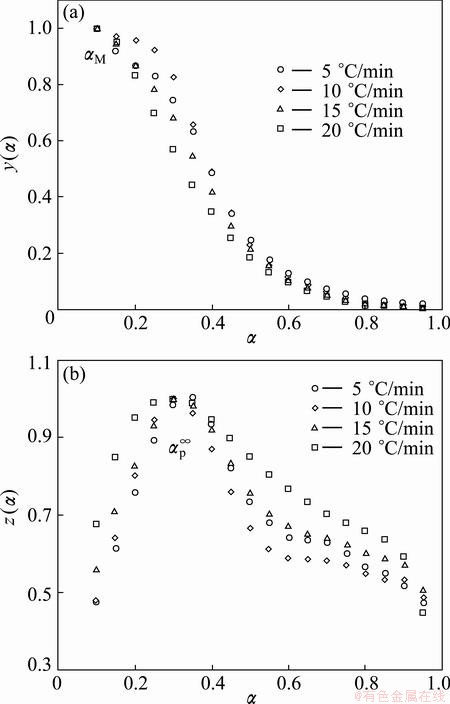
Fig. 6 Plots of normalized y(α) and z(α) against α for thermal decomposition of mechanically activated Ag₂O–graphite mixture for 2 h

Table 3 Characteristic peak conversion degrees, α_p, α_M and α_p^∞ for thermal degradation of as-received sample and mechanically activated Ag₂O–graphite powder for 2 and 4 h

According to the shape of y(α) and characteristic values of y(α) and z(α), it can draw a conclusion that the truncated Sestak-Berggren model [11,15,24,56-58] or extended Prout–Tompkins model (the regular Prout– Tompkins model is f(α)=α(1-α)), SB (m, n), is suitable for kinetic modeling of Ag₂O degradation. In addition, from Table 3, one can observe that 0<α_M<α_p^∞ and α_p^∞≠0.632 for all samples, which strongly indicated that the truncated SB (m, n) [11,57,58] was suitable. An empirical model for f(α) has been proposed [11,58]:

f(α)=α^m(1-α)ⁿ[-ln(1-α)]^s                                  (10)

According to the Sestak and Berggren model, the combination of m, n, and s represents a number of different reaction models. The increasing value of the exponent m indicates a more important role of the precipitated phase on the overall kinetics. It also appears that a higher value of the second exponent (n>1) indicates increasing reaction complexity [11, 57, 58]. Furthermore, value of the exponent s can give us information about the nucleation properties of a given complex mechanism of the tested process [11,57,58]. It is generally used in truncated form (s=0 in Eq. (10)). The truncated Sestak–Berggren model is an example of an autocatalytic model. According to the truncated SB (m, n) model and Eq. (3), Eq. (2) can be transformed into the following [11,57,58]:

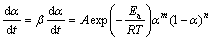           (11)

where m and n are the reaction orders. The ratio of m to n, p, equals α_M/(1-α_M) according to Refs. [11,15]. Thus, Eq. (11) can be transformed into the following:

    (12)

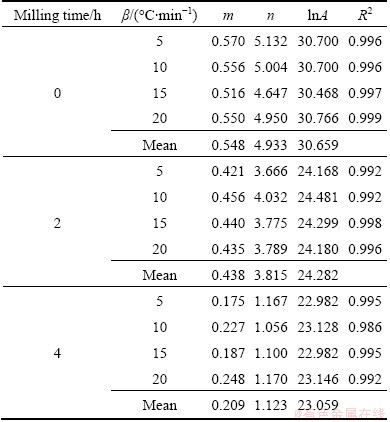
The kinetic parameter n can be derived from the slope of ln(βdα/dT)exp[E_a/(RT)] versus ln α^p(1-α) for 0.2≤α≤0.95 [59], and the intercept is ln A, and m=pn. These data perform good linearity (see Table 4). The values of m, n and ln A could be calculated from the intercept and slope of these fit straight lines as listed in Table 4. These kinetic parameters vary slightly with heating rates, with deviation less than 10% of their average values. In addition, the higher value of the kinetic parameter n (n>1) indicates the increasing complexity and decreasing the autocatalytic tendency of the degradation process [58]. Therefore, the thermal decomposition of as-received sample was a process with the complexity and the autocatalytic tendency higher and lower than Ag₂O–graphite powders mechanically activated for 2 and 4 h, respectively (the complexity point of view: 0>2 h>4 h and the autocatalytic tendency point of view: 0<2 h<4 h).

Table 4 Calculated kinetic parameters m, n and lnA for SB (m, n) model for thermal degradation of as-received sample and mechanically activated Ag₂O–graphite powder for 2 and 4 h

Substituting the calculated kinetic parameters (n, m, and ln A in Table 4 along with previously calculated E_a) into Eq. (11), the explicit rate equations for the decomposition reactions of as-received sample (the first step) and Ag₂O–graphite mixture mechanically activated for 2 and 4 h are obtained by Eqs. (13), (14) and (15), respectively:

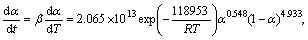    α∈[0,0.55] (0 h)                         (13)

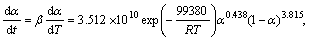    α∈[0,0.50] (2 h)                         (14)

    α∈[0,1] (4 h)                           (15)

To check the predictability of the explicit kinetic models (Eqs. (14) and (15)), the predicted rate curves for the different heating rates were calculated (see Fig. 7). From Fig. 7, it can be seen that there is a good agreement between the experimentally obtained βdα/dT-T curves and numerically calculated rate curves for the Ag₂O degradation process, using the corresponding kinetic triplets, hence the truncated SB (m, n) model is suitable for predicting kinetic rate of Ag₂O decomposition.

To determine the suitable kinetic model for the decomposition process of mechanically activated Ag₂O–graphite powder for 2 h in the range of α=0.50-0.95, we can apply the integral master plot method. Figure 8 shows the theoretical integral master curves for P_1/4 (full green line), P_1/3 (full blue line), P_1/2 (full red line) and A₄ (full yellow line) kinetic models, and also the experimental master curves (symbols). It could be seen from Fig. 8, the experimental master curves (at all heating rates) are in good agreement with the theoretical master curve for P_1/4 model. As a result, the decomposition process of mechanically activated Ag₂O–graphite powder for 2 h in the range of α=0-0.50 followed an autocatalytic model (Eq. (14)), while, in the range of α=0.50-1 followed an acceleratory rate model (nucleation mechanism).

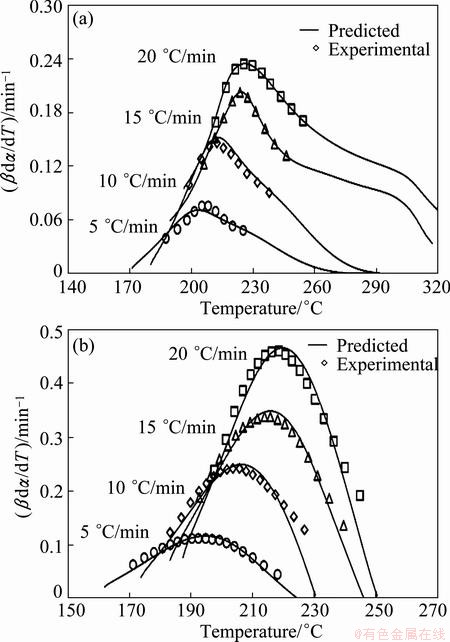
Fig. 7 Comparison of experimental reaction rate and that predicated from SB (m, n) model vs temperature for thermal decomposition of mechanically activated Ag₂O–graphite mixture for 2 h (a) and 4 h (b)

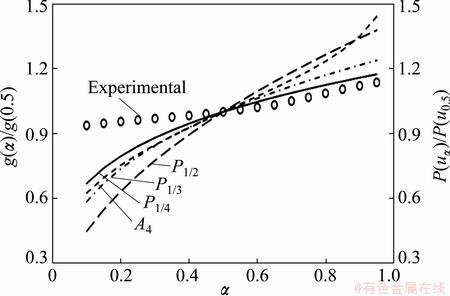
Fig. 8 Comparison between theoretical integral master curve for P_1/4 (g(α)=α^1/4), P_1/3 (g(α)=α^1/3), P_1/2 (g(α)=α^1/2) and A₄ (g(α)=[-ln(1-α)]^1/4) kinetic models and experimental master curve for thermal decomposition of mechanically activated Ag₂O–graphite mixture for 2 h

5 Conclusions

1) The decomposition of as-received Ag₂O–graphite mixture consists of two steps (using DSC curve). The results of the Vyazovkin method show that the first step of decomposition of as-received Ag₂O–graphite mixture is a complex process with the participation of at least two mechanisms and the second step is a single-step process (the average activation energy=(118.93±3.95) kJ/mol). The dependence of E_a on α, according to Vyazovkin method, for the first step (the first peak of DSC curve for as-received Ag₂O–graphite mixture) could be divided into two different regions (α≤0.55 and α>0.55). The average values of E_a for the first (0.10≤α≤0.55) and the second (0.55<α≤0.95) regions of the first step in as-received sample are (118.95±6.86) and (168.87±9.04) kJ/mol, respectively.

2) However, the difference between the maximum and minimum values of activation energy is less than 20%-30% of the average activation energy (99.38±2.36) kJ/mol, thermal decomposition of mechanically activated Ag₂O for 2 h is a multi-step process. This behavior could be related to the formation of Ag layer (due to the progress of α) and detachment of Ag layer (due to the increase in lattice strain within the interface) at the Ag₂O-graphite interface. Moreover, with increasing milling time to 4 h, the average particle size of precursor is reduced and decomposition reaction of Ag₂O is completed by the formation of Ag layer at the Ag₂O-graphite interface, So, thermal decomposition of sample milled for 4 h is a single-step process (the average E_a=(93.68±2.26) kJ/mol).

3) The thermal decomposition of Ag₂O-graphite mixture (as-received, the first step) is a process with the complexity and the autocatalytic tendency higher and lower than mechanically activated Ag₂O–graphite powders for 2 and 4 h, respectively (the complexity point of view: 0 h>2 h>4 h and the autocatalytic tendency point of view: 0 h<2 h<4 h).

References

[1] L’VOV B V. Kinetics and mechanism of thermal decomposition of silver oxide [J]. Thermochimica Acta, 1999, 333: 13-19.

[2] BENTON A F, DRAKE L C. Kinetics of reaction and adsorption in the system silver-oxygen [J]. American Chemical Society, 1934, 56: 255-263.

[3] HOOD G C, MURPHY G W. The decomposition of silver oxide—An autocatalytic reaction [J]. Chemical Education, 1949, 26: 169-172.

[4] GARNER W E, REEVES L W. The thermal decomposition of silver oxide [J]. Transactions of the Faraday Society, 1954, 50: 254-260.

[5] HERLEY P J, PROUT E G. The thermal decomposition of silver oxide [J]. American Chemical Society, 1960, 82: 1540-1543.

[6] ALLEN J. The thermal decomposition of silver (I) oxide [J]. Australian Journal of Chemistry, 1960, 13: 431-442.

[7] KHAYATI G R, JANGHORBAN K. The nanostructure evolution of Ag powder synthesized by high energy ball milling [J]. Advanced Powder Technology, 2012, 23: 393-397.

[8] KHAYATI G R, JANGHORBAN K. An investigation on the application of process control agents in the preparation and consolidation behavior of nanocrystalline silver by mechanochemical method [J]. Advanced Powder Technology, 2012, 23: 808-813.

[9] KHAYATI G R, JANGHORBAN K, SHARIAT M H. Isothermal kinetic study of mechanochemically and thermally synthesized Ag from Ag₂O [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(4): 935-942.

[10] KHAYATI G R, JANGHORBAN K. Preparation of nanostructure silver powders by mechanical decomposing and mechanochemical reduction of silver oxide [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(5): 1520-1524.

[11] SHAHCHERAGHI S H, KHAYATI G R. Kinetics analysis of the non-isothermal decomposition of Ag₂O-graphite mixture [J]. Transactions of Nonferrous Metals Society of China, 2014, 14(9): 2991-3000.

[12] TOKUMITSU K. Reduction of metal oxides by mechanical alloying method [J]. Solid State Ionics, 1997, 101-103: 25-31.

[13] BALZAR D. X-ray diffraction line broadening: Modeling and application to high-T_c superconductors [J]. Journal of Research of the National Institute of Standards and Technology, 1993, 98: 321-353.

[14] WILLIAMSON G K, HALL W H. X-ray line broadening from filed aluminum and wolfram [J]. Acta Metallurgica, 1953, 1: 22-31.

[15] MALEK J. The kinetic analysis of non-isothermal data [J]. Thermochimica Acta, 1992, 200: 257-269.

[16] MONSERRAT S, MALEK J. A kinetic analysis of the curing reaction of an epoxy resin [J]. Thermochimica Acta, 1993, 228: 47-60.

[17] FRIEDMAN H L. Kinetics of thermal decomposition of char-forming plastics from thermogravimetry: Application to a phenolic plastic [J]. Polymer Science: Polymer Chemistry Edition, 1964, 6: 183-195.

[18] SENUM G I, YANG R T. Rational approximations of the integral of the Arrhenius function [J]. Thermal Analysis and Calorimetry, 1977, 11: 445-447.

[19] VYAZOVKIN S. Model-free kinetics: Staying free of multiplying entities without necessity [J]. Thermal Analysis and Calorimetry, 2006, 83: 45-51.

[20] CHRISSAFIS K. Complementary use of isoconversional and model-fitting methods [J]. Thermal Analysis and Calorimetry, 2009, 95: 273-283.

[21] KHASSIN A A, FILONENKO G A, MINYUKOVA T P, MOLINA I Y, PLYASOVA L M, LARINA T V, ANUFRIENKO V F. Effect of anionic admixtures on the copper–magnesium mixed oxide reduction [J]. Reaction Kinetics, Mechanisms and Catalysis, 2010, 101: 73-83.

[22] MUKHERJEE A, MISHRA S, KRISHNAMURTHY N. Thermogravimetric studies and kinetics of decomposition of ammonium yttrium fluoride [J]. Reaction Kinetics, Mechanisms and Catalysis, 2011, 103: 53-70.

[23] JOHN M J, MURALEEDHARAN K, MUJEEB V M A, KANNAN M P, DEVI T G. Effect of pre-compression on the kinetics of thermal decomposition of pure and doped sodium oxalate under isothermal conditions [J]. Reaction Kinetics, Mechanisms and Catalysis, 2012, 106: 355-367.

[24] EVARD E A, GABIS I E, MURZINOVA M A. Kinetics of hydrogen liberation from stoichiometric and nonstoichiometric magnesium hydride [J]. Materials Science, 2007, 43: 620-633.

[25] COATS A W, REDFERN J P. Kinetic parameters from thermogravimetric data [J]. Nature, 1964, 201: 68-69.

[26] LESNIKOVICH A I, LEVCHIK S V. A method of finding invariant values of kinetic parameters [J]. Thermal Analysis and Calorimetry, 1983, 27: 89-94.

[27] KISSINGER H E. Variation of peak temperature with heating rate in differential thermal analysis [J]. Research of the National Bureau of Standards, 1956, 57: 217-221.

[28] KISSINGER H E. Reaction kinetics in differential thermal analysis [J]. Analytical Chemistry, 1957, 29: 1702-1706.

[29] MITTEMEIJER E J. Analysis of the kinetics of phase- transformations [J]. Materials Science, 1992, 27: 3977-3987.

[30] STARINK M J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods [J]. Thermochimica Acta, 2003, 404: 163-176.

[31] GUPTA A K, JENA A K, CHATURVEDI M C. A differential technique for the determination of the activation-energy of precipitation reactions from differential scanning calorimetric data [J]. Scripta Metallurgica, 1988, 22: 369-371.

[32] VYAZOVKIN S, WIGHT C A. Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data [J]. Thermochimica Acta, 1999, 340-341: 53-68.

[33] VYAZOVKIN S. Thermal analysis [J]. Analytical Chemistry, 2010, 82: 4936-4949.

[34] SBIRRAZZUOLI N. Is the Friedman method applicable to transformations with temperature dependent reaction heat? [J]. Macromolecular Chemistry and Physics, 2007, 208: 1592-1597.

[35] VYAZOVKIN S, BURNHAM A K, CRIADO J M, PEREZ-MAQUEDA L A, POPESCU C, SBIRRAZZUOLI N. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data [J]. Thermochimica Acta, 2011, 520: 1-19.

[36] VYAZOVKIN S, SBIRRAZZUOLI N. Kinetic analysis of isothermal cures performed below the limiting glass transition temperature [J]. Macromolecular Rapid Communications, 2000, 21: 85-90.

[37] VYAZOVKIN S. Modification of the integral isoconversional method to account for variation in the activation energy [J]. Computational Chemistry, 2001, 22: 178-183.

[38] GASKELL D R. Introduction to the thermodynamics of Materials [M]. 5th ed. CRC Press, 2003.

[39] YANG N, AOKI K, NAGASAWA H. Thermal metallization of silver stearate-coated nanoparticles owing to the destruction of the shell structure [J]. Physical Chemistry B, 2004, 108: 15027-15032.

[40] EL-ESKANDARANY M S, AOKI K, SUMIYAMA K, SUZUKI K. Cyclic phase transformations of mechanically alloyed Co₇₅Ti₂₅ powders [J]. Acta Materialia, 2002, 50: 1113-1123.

[41] HARRIS S R, PEARSON D H, GARLAND C M, FULTZ B. Chemically disordered Ni₃Al synthesized by high vacuum evaporation [J]. Journal of Materials Research, 1991, 6: 2019-2021.

[42] WELHAM N J. Mechanical activation of the solid-state reaction between Al and TiO₂ [J]. Materials Science and Engineering A, 1998, 255: 81-89.

[43] JANKOVIC B, MENTUS S, JELIC D. A kinetic study of non-isothermal decomposition process of anhydrous nickel nitrate under air atmosphere [J]. Physica B, 2009, 404: 2263-2269.

[44] BOONCHOM B. Kinetics and thermodynamic properties of the thermal decomposition of manganese dihydrogenphosphate dehydrate [J]. Chemical & Engineering Data, 2008, 53: 1533-1538.

[45] GAO X, DOLLIMORE D. The thermal decomposition of oxalates: Part 26. A kinetic study of the thermal decomposition of manganese (II) oxalate dehydrate [J]. Thermochimica Acta, 1993, 215: 47-63.

[46] VLAEV L T, NIKOLOVA M M, GOSPODINOV G G. Non-isothermal kinetics of dehydration of some selenite hexahydrates [J]. Solid State Chemistry, 2004, 177: 2663-2669.

[47] BOONCHOM B. Kinetic and thermodynamic studies of MgHPO₄·3H₂O by non-isothermal decomposition data [J]. Thermal Analysis and Calorimetry, 2009, 98: 863-871.

[48] GALVITA V, SUNDMACHER K. Redox behavior and reduction mechanism of Fe₂O₃-CeZrO₂ as oxygen storage material [J]. Journal of Materials Science, 2007, 42: 9300-9307.

[49] FERREIRA C I, CASTEL C D, OVIEDO M A S, MAULER R S. Isothermal and non-isothermal crystallization kinetics of polypropylene/exfoliated graphite nanocomposites [J]. Thermochimica Acta, 2013, 553: 40-48.

[50] JOSEPH J, NAIR T D R. Effect of metal oxide catalysts on thermal decomposition of potassium bromate [J]. Thermal Analysis and Calorimetry, 1978, 14: 271-279.

[51] VYAZOVKIN S, WIGHT C A. Kinetics in solids [J]. Annual Review of Physical Chemistry, 1997, 48: 125-149.

[52] VYAZOVKIN S, SBIRRAZZUOLI N. Kinetic methods to study isothermal and non-isothermal epoxy-anhydride cure [J]. Macromolecular Chemistry and Physics, 1999, 200: 2294-2303.

[53] SBIRRAZZUOLI N, GIRAULT Y, ELEGANT L. Simulations for evaluation of kinetic methods in differential scanning calorimetry. Part 3—Peak maximum evolution methods and isoconversional methods [J]. Thermochimica Acta, 1997, 293: 25-37.

[54] VYAZOVKIN S. Evaluation of activation energy of thermally stimulated solid state reactions under arbitrary variation of temperature [J]. Journal of Computational Chemistry, 1997, 18: 393-402.

[55] WAN J, BU Z Y, XU C J, LI B G, FAN H. Learning about novel amine-adduct curing agents for epoxy resins: Butyl-glycidylether- modified poly (propyleneimine) dendrimers [J]. Thermochimica Acta, 2011, 519: 72-82.

[56] MALEK J. A computer program for kinetic analysis of non-isothermal thermoanalytical data [J]. Thermochimica Acta, 1989, 138: 337-346.

[57] SIMON P. Forty years of the Sestak–Berggren equation [J]. Thermochimica Acta, 2011, 520: 156-157.

[58] SESTAK J, BERGGREN G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures [J]. Thermochimica Acta, 1971, 3: 1-12.

[59] KOGA N. Kinetic analysis of thermoanalytical data by extrapolating to infinite temperature [J]. Thermochimica Acta, 1995, 258: 145-159.

非等温条件下机械活化Ag₂O-石墨混合物Arrhenius参数的测定

Seyed Hadi SHAHCHERAGHI¹, Gholam Reza KHAYATI²

1. Department of Mineral Processing Engineering, Shahid Bahonar University of Kerman, Kerman, Iran;

2. Department of Materials Science and Engineering, Shahid Bahonar University of Kerman, Kerman, Iran

摘  要：采用DSC和TGA及模型拟合Malek法和无模型改进Vyazovkin等转化率法研究机械化学还原Ag₂O和石墨混合物的非等温动力学。为了测定动力学参数，选取研磨活化2 h和4 h的及未球磨的Ag₂O-石墨混合物为样品。基于Vyazovkin法计算得到的活化能最大值和最小值之间的差比平均活化能小20%~30%((99.38±2.36) kJ/mol)，Ag₂O 机械活化2 h的热分解是一个多步过程，机械活化4 h的热分解是一个单步过程(平均活化能为(93.68±2.26) kJ/mol)。动力学模型表明，未球磨的Ag₂O-石墨混合物的热分解过程比其他的复杂。Ag₂O-石墨混合物的自动催化趋势比其他的低。

关键词：机械活化；Vyazovkin法；动力学模型；Siestas–Berggren模型；积分主曲线法；氧化银

(Edited by Xiang-qun LI)

Corresponding author: Gholam Reza KHAYATI; Tel: +98-915-1903477; Fax: +98-341-2114053; E-mail: khayati@uk.ac.ir; khayatireza@gmail.com

DOI: 10.1016/S1003-6326(14)63561-5