J. Cent. South Univ. (2019) 26: 2814-2821

DOI: https://doi.org/10.1007/s11771-019-4215-3

Influence of positioning errors of optical shaping components for single emitter laser diode on beam shaping effects

YAN Yi-xiong(严一雄), ZHENG Yu(郑煜), DUAN Ji-an(段吉安)

State Key Laboratory of High Performance Complex Manufacturing, College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: Beam shaping is required for semiconductor lasers to achieve high optical fiber coupling efficiency in many applications. But the positioning errors on optics may reduce beam shaping effects, and then lead to low optical fiber coupling efficiency. In this work, the positioning errors models for the single emitter laser diode beam shaping system are established. Moreover, the relationships between the errors and the beam shaping effect of each shapers are analysed. Subsequently, the relationship between the errors and the optical fiber coupling efficiency is analysed. The result shows that position errors in the Z axis direction on the fast axis collimator have the greatest influence on the shaping effect, followed by the position errors in the Z axis direction on the converging lens, which should be strictly suppressed in actual operation. Besides, the position errors have a significant influence on the optical fiber coupling efficiency and need to be avoided.

Key words: single emitter laser diode; beam shaping; positioning error; coupling efficiency

Cite this article as: YAN Yi-xiong, ZHENG Yu, DUAN Ji-an. Influence of positioning errorsof optical shaping components for single emitter laser diode on beam shaping effects [J]. Journal of Central South University, 2019, 26(10): 2814-2821. DOI: https://doi.org/10.1007/s11771-019-4215-3.

1 Introduction

Semiconductor lasers have a wide range of applications in various fields. High beam quality has been required in most applications [1-3]. However, laser diodes have serious astigmatism resulting in a larger difference in the divergence angle between the fast and slow axes, which makes it poor beam quality [4-6]. The most effective way to improve beam quality is to use specific lens for beam shaping [7-9]. For this work, various solutions have been proposed in the past decades. Early research achievement including CHIBA et al [10] obtained gradient index lens for laser diode array collimation. EHLERS et al [11] proposed a pair of micro step-mirrors for shaping diode laser array. In recent years, ZHEN et al [12] reported a double axial hyperboloidal lens which can focus the laser from both two axes to make the shaping system simpler, integrated and efficient. XIONG et al [13] indicated a variable curvature radius slow axis collimator (SAC), which can effectively improve the beam collimation. Most of researchers are committed to find new beam shaping methods and constantly improving beam quality.

Additionally, the design and analysis of lens surface deformation error in high power laser diode (HPLD) have been studied in many literatures. For example, MALACARNE et al [14] and LIU et al [15] proposed two theoretical models for exploring the surface deformation of optical components. However, there are few literatures on the research and analysis of positioning errors, and this is the key to HPLD packaging and the prerequisite for its application.

In this paper, theoretical modelling has been established. Besides, the effect of the positioning errors on the shaping performance of the shapers has been analysed as a core research. Moreover, the influence of optical fiber alignment errors on optical fiber coupling efficiency is provided.

2 Beam shaping system theoretical analysis and model

Laser diode beam is demanded to enhance beam quality for eventually being coupled into the optical fiber. Based on ISO standard, one of the most general ways to evaluate the beam quality is the beam parameter product (BPP), which can be expressed as Eq. (1) [7, 16].

BPP=ω₀×θ₀                                               (1)

where ω₀ is the waist radius, θ₀ is the far filed beam divergence.

In order to satisfy the request of the optical fiber coupling, it is essential that the diameter of the shaped beam spot is smaller than the core diameter of the fiber, and the beam divergence angle is smaller than the angle corresponding to the numerical aperture of the fiber, which can be expressed as Eqs. (2) and (3).

d_beam<φ_fiber                                                (2)

θ_beamfiber                       (3)

where d_beam is the spot diameter of the shaped beam; φ_fiber is the core diameter of the fiber; moreover, θ_beam is the beam divergence angle, and arcsin(NA)_fiber is the aperture angle of fiber. As mentioned before, the beam quality of a semiconductor laser is poor. The spot is elliptical, and the divergence angles of the beam are greatly different in the fast axis direction and the slow axis direction. However, fiber coupling requires equalization of the fast and slow axes of the coupled beam. Therefore, in the beam shaping operation, the difference between the spot size and the divergence angle of two axis should be mainly aimed at. In this work, the difference in spot size and the difference in divergence angle in two axes are represented by R_fast/slow, which is shown as Eq. 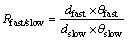(4).

                      (4)

where d_fast and d_slow are the diameters of the spot in fast axis and slow axis, respectively; θ_fast and θ_slow are the divergence angle in fast axis and slow axis, respectively. R_fast/slow is the evaluation factor of the beam quality, the closer the ratio is to 1, the better the beam quality is.

For the single emitter laser diode beam shaping system model, the power of the laser source is 8 W, and the divergence angles in fast and slow axes are 7° and 27°, respectively. Firstly, the beam passes through fast axis collimator (FAC) and slow axis collimator (SAC) to reduce the divergence angles in the fast axis and slow axis. Then, R_fast/slow is further decreased by using beam expander. The converging lens is used to minify the beam spot diameter at both direction subsequently. Finally, the beam has been coupled into optical fiber successfully. The schematic of the system is shown in Figure 1.

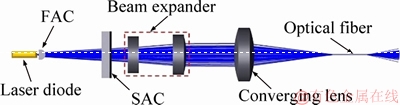
Figure 1 Schematic of beam shaping and coupling system

Analysis of the influence of shapers’ beam shaping effect is divided into the following steps: firstly, the optimal installation position, which has a tight connection with the greatest beam quality (R_fast/slow closest to 1) has been found. Then, the positioning errors of shapers tip in the space, including position errors and angle errors, are set to all shapers. Finally, the relationship between each positioning error and the shaping effect is generated. In this essay, the influences of four shapers’ beam shaping quality have been analysed separately [17]. Our research object is influence of the positioning error of each mirror to guide the packaging process. As mentioned before, the influence of lens surface deformation error has been studied in many literatures. In this part of the work, the errors caused by deformation and wear of the optical elements are not taken into account.

The error models of four shaping devices are successively established. Error models simulate various situations when each of shapers has 6-degree-of-freedom position error and angle error, which is shown in Figure 2, where △X, △Y, △Z represent the position error on 3 axes, respectively. Moreover, θX, θY, θZ represent the angle error on 3 axes, respectively.

Additionally, analysis of the impact of fiber alignment error on the optical fiber coupling is similar to before. We firstly find the optimal installation position of optical fiber where the whole system can achieve maximum coupling efficiency (96%). Then 6-degree-of-freedom position errors and angle errors have been set on the model which is shown as Figure 3. Finally, the relationship between each alignment errors and the optical fiber coupling efficiency is calculated.

3 Results and discussion

The influence of all positioning errors of optical shaping components on beam shaping effects is calculated by optical simulation software, as shown below.

3.1 Influence of positioning errors on beam shaping effect of FAC

The influence of position errors on beam shaping of fast axis collimator has been examined. The result is shown as Figure 4.

As illustrated in Figure 4, the abscissa is the magnitude of the position error, the zero point is the optimal installation position, the ordinate is R_fast/slow of the shaped beam. The position errors in three directions are represented by three different curves, which are △X_fast, △Y_fast and △Z_fast. The △X_fast curve is a straight line perpendicular to the ordinate at 1. The △Y_fast curve is basically a Gaussian distribution, the greater the absolute value of the error, the smaller the ratio. The △Z_fast curve is roughly inversely distributed in the error interval from -0.3 mm to zero point and exponentially distributed in the error interval from zero point to 0.3 mm. It can be summarized as follows: the position error in the X-axis has no effect on the beam shaping of fast axis collimator, in other words, the error in this direction needs not be worried in actual operation;The position error in the Z axis direction has the greatest influence on the beam shaping effect of the FAC, position error of about 0.3 mm will cause R_fast/slow greater than 100% compared to 1, which means that the beam shaping effect will be reduced to the lowest. Moreover, the downward trend of △Z_fast curve began to slow down after the zero point. It indicates that the influence of the direction of the error towards the direction away from the laser source will be gradually weaker than that near the light source.

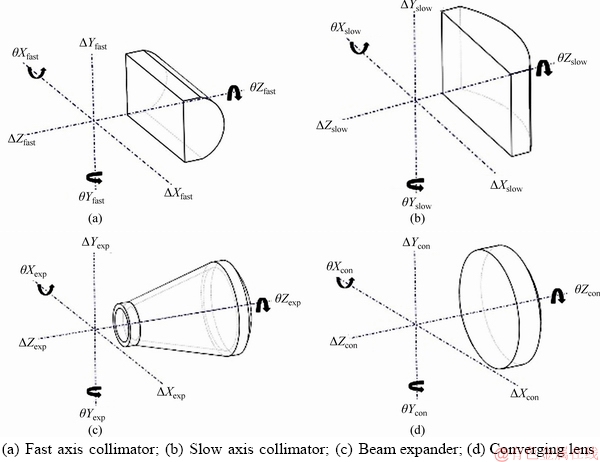
Figure 2 Shapers position error and angle error models:

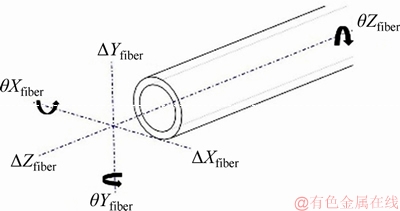
Figure 3 Fiber alignment errors model

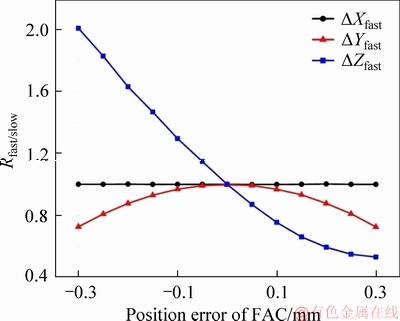
Figure 4 Influence of position errors on beam shaping of FAC

The influence of angle errors on beam shaping of fast axis collimator has been examined. The result is shown as Figure 5.

In order to make the trend of curve more apparent, the angle errors range is set between -20° and 20°. Besides, the magnitude of the errors that may occur in the actual operation is represented by partial view. The angle errors in three directions are represented by three different curves, which are θX_fast, θY_fast and θZ_fast. The θX_fast curve is basically a Gaussian distribution, and the θY_fast curve almost coincides with θX_fast curve, but the upward trend of the curve at the left of zero point is slightly more pronounced than the downward trend of the curve at the right. The θZ_fast curve is basically an inverse Gaussian distribution. It can be summarized as follows: the angle error in the Y axis direction has the relatively large impact on the beam shaping effect of the FAC. Nevertheless, according to the partial view, the angle error in the Z axis direction almost has little impact on shaping. Moreover, the angle errors in the other two directions will not make the beam shaping effect less than 98%. In contrast, the influence of angle errors on the FAC shaping effect is far less than the influence of position errors on it.

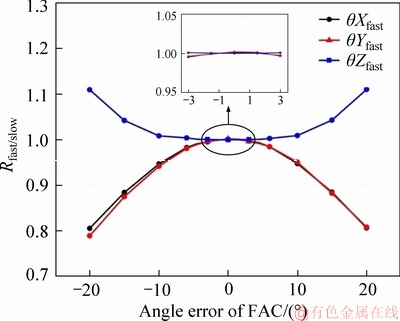
Figure 5 Influence of angle errors on beam shaping of FAC

3.2 Influence of positioning errors on beam shaping effect of SAC

The impact of position errors on beam shaping of slow axis collimator has been simulated, which is shown as Figure 6.

The △X_slow curve is approximately logarithmic distribution. The △Y_slow curve is almost a straight line perpendicular to the ordinate at 1. Its slight fluctuation is caused by the calculation error of the optical ray tracing. However, the fluctuation is very weak compared to other curve changes and therefore can be gnored. The △Z_slow curve is basically an inverse Gaussian distribution. It can be summarized as follows: the position error in the Y-axis has no effect on the beam shaping of slow axis collimator; the relatively serious impact on the beam shaping effect is the position error in the X axis direction. However, the partial view shows that the position errors basically do not affect the shaping of slow axis collimator. The beam shaping effect will not less than 98% if △Z_slow is smaller than 0.5 mm.

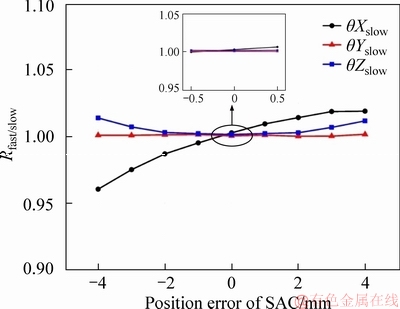
Figure 6 Influence of position errors on beam shaping of SAC

The impact of angle errors on beam shaping of slow axis collimator has been simulated, which is shown as Figure 7.

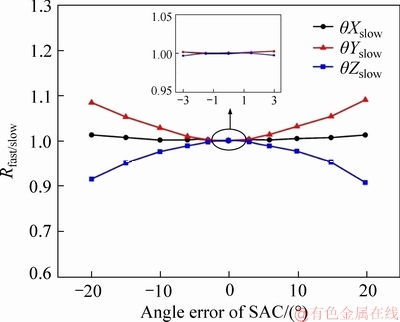
Figure 7 Influence of angle errors on beam shaping of SAC.

The θX_slow curve and θY_slow curve are inverse Gaussian, and θZ_slow is a Gaussian distribution. It presents that the angle errors have nearly no effect on shaping during the actual operating.

According to the results, it can be found that the SAC beam shaping effect is much less sensitive to position errors than FAC. But the same thing is that the impact of the angle errors on them is minimal.

3.3 Influence of positioning errors on beam shaping effect of beam expander

The impact of position errors and angle errors on beam shaping of beam expander has been simulated, which are shown in Figures 8 and 9, respectively.

The △X_exp curve and θX_exp curve are inverse Gaussian, the upward trend of the curve at the right of zero point is more pronounced than the downward trend of the curve at the left. The △Y_exp curve and θY_exp curve are Gaussian distribution, the upward trend of the θY_exp curve at the left of zero point is more pronounced than the downward trend of the curve at the right. The △Z_exp curve and θZ_exp curve are linearly distributed, θZ_exp curve shows that it has no effect on the beam shaping effect.

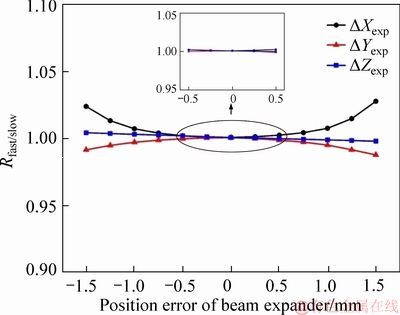
Figure 8 Influence of position errors on beam shaping of beam expander

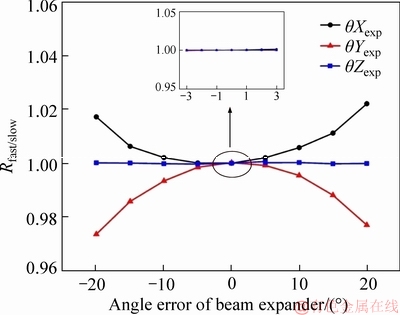
Figure 9 Influence of angle errors on beam shaping of beam expander

Throughout two partial views, the impact of the positioning errors on the beam shaping effect of the beam expander is minute.

3.4 Influence of positioning errors on beam shaping effect of converging lens

The impact of position errors on beam shaping of converging lens has been simulated, which is shown in Figure 10.

The △X_con curve and △Y_con curve are Gaussian distributed. The △Z_con curve is distributed as an exponential function in the error interval from -1.5 mm to zero point, and is a logarithmic function distribution in the error interval from zero point to 1.5 mm. It can be summarized as follows: the position error in the Z axis direction has the greatest impact on the beam shaping effect of the converging lens. 0.5 mm position error will cause the beam shaping effect to drop to 75%. Moreover, the influence of the direction of the error towards the direction away from the laser source will be gradually greater than that near the light source.

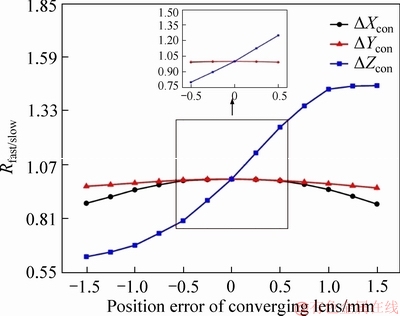
Figure 10 Influence of position errors on beam shaping of converging lens

The influence of angle errors on beam shaping of converging lens has been simulated, which is shown as Figure 11.

Figure 11 Influence of angle errors on beam shaping of converging lens

The θX_con curve is logarithmic in the angle error range of -20° to -10°, and is a Gaussian function distribution in the error interval from -10° to 10°, and exponentially distributed in the range of 10° to 20°. The θY_con curve is nearly a Gaussian function distribution. Moreover, the θZ_con has no impact on beam shaping of converging lens. According to the partial view, convergent lens beam shaping effect is most sensitive to the θY_con. Although 3° angle error on converging lens can only lead to the beam shaping effect decrease to 97.5%, it is quite obvious compared to the influence of angle errors on beam expander.

3.5 Influence of fiber alignment errors on optical fiber coupling efficiency

The influence of position errors and angle errors on coupling efficiency has been examined, which are shown in Figures 12 and 13, respectively.

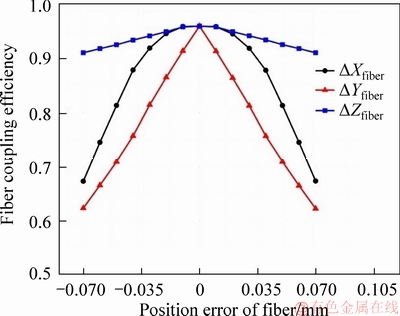
Figure 12 Influence of position errors on optical fiber coupling efficiency

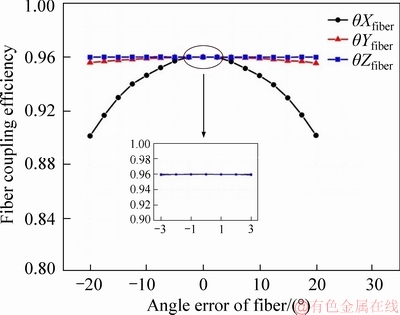
Figure 13 Influence of angle errors on optical fiber coupling efficiency

Different from the coordinate map before, the ordinate is the optical fiber coupling efficiency. The △X_fiber curve is roughly a Gaussian distribution. The △Y_fiber curve is a positive ratio function distribution in the position error range of -0.07 mm to zero point, and is an inversely proportional function distribution in the range of zero point to 0.07mm. The △Z_fiber curve is similar to △Y_fiber curve, but the change trend is much sluggish. In contrast, optical fiber coupling efficiency is most sensitive to the △Y_fiber. 0.07 mm position error may cause the optical fiber coupling efficiency decrease to 62.5%.

The θY_fiber curve is a Gaussian function distribution. The θY_fiber only has tiny influence on optical fiber coupling efficiency, and the θY_fiber has no impact on optical fiber coupling efficiency. In contrast, the optical fiber coupling efficiency is most sensitive to θX_fiber. However, according to the partial view, angle errors have essentially no effect on optical fiber coupling efficiency.

4 Conclusions

This paper focuses on packaging and installation issues. The influence law of the positioning errors on the shaping effect of the shaping optics is demonstrated, which can be used to guide the packaging process. The position error in the Z axis direction of the FAC has the greatest impact on the beam shaping effect. When △Z_fast=-0.3 mm, the beam shaping effect will be reduced to the lowest. Moreover, the position error in the Z axis direction of the converging lens has serious influence on the beam shaping effect. When △Z_con=0.5 mm, the beam shaping effect will be decreased to 75%. These indicate that the position errors of fast axis collimator and converging lens in the Z axis direction need to be strictly avoided in actual operation. The effects of other errors are not noticeable. Especially for beam expander, the influence of position and angle errors can be basically negligible in the actual operating. For optical fiber coupling, the position errors affect the optical fiber coupling efficiency more serious than angle errors, which should be noted in the actual operation.

References

[1] FRIEDRICH D. High power diode lasers: Technology and applications [J]. Proceedings of SPIE-The International Society for Optical Engineering, 2007, 3888: 162-174. DOI: 10.1117/12.377093.

[2] MURPHY E. The semiconductor laser: Enabling optical communication [J]. Nature Photonics, 2010, 4(5): 287-287. DOI: 10.1038/nphoton.2010.107.

[3] FRED M D. Laser beam shaping [J]. Optics & Photonics News, 2003, 14(4): 30-35.

[4] HANNA D C, CLARKSON W A. Two-mirror beam-shaping technique for high-power diode bars [J]. Optics Letters, 1996, 21(6): 375-377. DOI: 10.1364/OL.21.000375.

[5] DICKEY F M, SHEALY D L. Laser beam shaping V [J]. Proc Spie, 2004, 5175(4): 751-760.

[6] LEGER J R, GOLTSOS W C. Geometrical transformation of linear diode-laser arrays for longitudinal pumping of solid-state lasers [J]. IEEE Journal of Quantum Electronics, 1992, 28(4): 1088-1100. DOI:10.1109/3.135232.

[7] LIU X S, ZHAO W, XIONG L L, LIU H. Packaging of high power semiconductor lasers [M]. Heidelberg, Springer, 2014: 107-115. DOI:10.1007/978-1-4614-9263-4.

[8] HEINEMANN S. Fiber-coupled diode lasers and beam-shaped high-power stacks [J]. Proceedings of SPIE- The International Society for Optical Engineering, 1998, 3267: 116-124. DOI:10.1117/12.308099.

[9] KHLER B, BRAND T, HAAG M, BIESENBACH J. Wavelength stabilized high-power diode laser modules [C]// High-Power Diode Laser Technology and Applications VII. International Society for Optics and Photonics, 2009: 719810-719810-12. DOI:10.1117/12.809541.

[10] CHIBA K, YAMAGUCHI S, KOBAYASHI T, SAITO Y. Collimation of emissions from a high-power multistripe laser-diode bar with multiprism array coupling and focusing to a small spot [J]. Optics Letters, 1995, 20(8): 898-900. DOI: 10.1364/OL.20.000898.

[11] EHLERS B, DU K, BAUMANN M, TREUSCH H. Beam shaping and fiber coupling of high-power diode laser arrays [C]// Lasers in Material Processing. International Society for Optics and Photonics, 1997: 639-644. DOI: 10.1117/12. 281128.

[12] TIAN Z N, WANG L J, CHEN Q D, JIANG T, QIN L, SUN H B. Beam shaping of edge-emitting diode lasers using a single double-axial hyperboloidal micro-lens [J]. Optics Letters, 2013, 38(24): 5414-7. DOI: 10.1364/OL.38.005414.

[13] XIONG L L, CAI L, ZHENG Y F, LIU H. Slow axis collimation lens with variable curvature radius for semiconductor laser bars [J]. Optics & Laser Technology, 2016, 77: 1-5. DOI: 10.1016/j.optlastec.2015.08.004.

[14] MALACARNE L C, ASTRATH N G C, BAESSO M L. Unified theoretical model for calculating laser-induced wavefront distortion in optical materials [J]. Journal of the Optical Society of America B, 2012, 29(7): 1772-1777. DOI: 10.1364/josab.29.001772.

[15] LIU M, LI B, WANG Y. Accurate determination of subnanoscale deformation with combined laser calorimetry and surface thermal lens technique [J]. Applied Physics Letters, 2009, 94(13): 650. DOI: 10.1063/1.3106630.

[16] FANG F Z, XIONG Z, HU X T. Ultra-precision machining of reflector array for laser diode beam shaping [J]. Optoelectron Lett, 2007, 3(2): 141-143. DOI: 10.1007/ s11801-007-7020-4.

[17] LI D X, ZHANG J F, ZHANG Y L, FENG P F. Modeling, identification and compensation for geometric errors of laser annealing table [J]. Journal of Central South University, 2014, 21(3): 904-911. DOI: 10.1007/s11771-014-2017-1.

(Edited by HE Yun-bin)

中文导读

单发射激光器二极管光学整形元件定位误差对光束整形效果的影响

摘要：半导体激光器在许多应用中为获得高光纤耦合效率需要进行光束整形。但光学系统若存在定位误差将会降低光束的整形效果，以导致光纤耦合效率降低。本文建立了单发射激光器二极管光束整形系统的定位误差模型。然后分析了个整形光器件的误差和光束整形效果的关系。还分析了误差和光纤耦合效率的关系。结果表明，快轴准直透镜在Z轴方向上存在位置误差对光束整形效果的影响最大，其次是会聚透镜在Z轴方向上的位置误差对光束整形效果的影响，这在实际操作中应严格避免。此外，光纤存在位置误差对光纤耦合效率影响较大，也需要尽量避免。

关键词：单发射激光器二极管；光束整形；定位误差；耦合效率

Foundation item: Project(51475479) supported by the National Natural Science Foundation of China; Project(2017YFB1104800) supported by the National Key Research and Development Program of China; Project(2016GK2098) supported by the Key Research and Development Program of Hunan Province, China; Project(ZZYJKT2017-07) supported by the State Key Laboratory of High Performance Complex Manufacturing, Central South University, China; Project(JMTZ201804) supported by the Key Laboratory for Precision & Non-traditional Machining of Ministry of Education, Dalian University of Technology, China

Received date: 2018-08-30; Accepted date: 2019-06-17

Corresponding author: ZHENG Yu, PhD, Associate Professor; Tel: +86-731-88660304; E-mail: zhengyu@csu.edu.cn; ORCID: 0000-0002-0411-3868