DOI: 10.11817/j.ysxb.1004.0609.2020-37638
铝合金板材挤压自弯曲成形机理及模具优化设计
闵范磊,朱光明,高绪杰,岳博文,刘惠苹,郭娜娜,翟晓庆
(山东理工大学 机械工程学院,山东 淄博 255000)
摘要:由连续介质力学,得到板材在理想自弯曲过程中,出口速度分布与弯曲曲率半径的关系,并提出一种铝合金板材自弯曲挤压新工艺,通过设计异形导流腔结构,使模腔内金属产生不均匀流动,从而直接挤出弯曲型材;利用数值模拟,分析了板材挤压过程的自弯曲变形机理、金属流动特点、以及残余应变的分布;通过选取型腔结构因子与挤压速度作为变量,采用拉丁超立方抽样方法结合模拟计算,建立了挤出型材弯曲曲率半径的响应面预测模型,在指定弯曲半径为1900mm的条件下,建立附带罚函数的目标函数优化模型,利用粒子群算法得到最优模腔结构与工艺参数,并进行试模实验,实验结果显示,自弯曲板材挤出稳定,测得曲率半径为2071mm,弯曲板材内外侧晶粒大小均匀。
关键词:铝合金弯曲板材;自弯曲成形;关系推导;机理分析;优化设计
中图分类号:TG379 文献标识码:A 1
弯曲型材广泛应用于建筑、汽车、航空等制造领域。传统弯曲型材的成形工艺,通常是先挤压后弯曲;常用的弯曲加工方式主要有拉弯、绕弯和滚弯[1-3],在弯曲加工过程中,易导致型材回弹、起皱、微裂纹、成形精度低等缺陷[4-7];传统弯曲加工方法带有较强的经验性,成形缺陷也难以避免。
近年来,在提高弯曲型材成形质量方面,国内外学者开展了许多研究:一种方法是增设外部弯曲设备,通过影响挤压模具出口处的材料流动,使挤压弯曲一体化。KLEINER等[8]提出了弯曲型材挤出工艺(CPE),使金属挤压和弯曲连续进行,从而提高弯曲型材的制造效率;MüLLER[9]在挤压模后添加多个环形圆盘作为弯曲装置,通过调整圆盘的位置,实现了“Z”型材与管材的挤压弯曲一次成形。另一种方法是通过改变模具结构,使材料在挤压过程中发生不均匀流动,型材挤出后自然弯曲成形,此方法避免了传统弯曲加工造成的成形缺陷,同时提高了制造效率。SHIRAISHI等人[10]利用倾斜导流腔结构的挤压模具,挤压直接得到弯曲棒材和管材,并研究了模具倾斜角、模具孔径高度和宽度对型材曲率的影响。弯曲管也可以通过多孔挤压(MHE)[11]形成,此工艺基于模具的出口位置偏离对称中心轴的方法,导致金属流动不均匀,进而挤出弯曲型材。石磊等[12-13]通过在挤压模具内增设辅助挤压杆,动态调控挤压过程中金属的不均匀流动,实现了镁合金弯管件的挤出成形;ZHOU等[14]通过差速侧向挤压工艺(DVSE),使用两个相对的冲头直接一次挤出弯曲管材。
综上所述,通过特殊的模具结构可以得到挤压弯曲的零件;许多学者也研究了模具结构参数对弯曲曲率半径的影响。实际上,挤压型材的曲率半径是由模具出口处的不均匀挤压速度分布决定的,而出口速度分布与弯曲曲率半径之间的关系尚未建立,自弯曲挤压模具也多凭经验设计,所以,自弯曲挤压成形工艺需要进一步理论化与量化,以供深入的科学研究与实际工程应用。
本文通过连续介质力学理论,推导出自弯曲挤出成形工艺下,型材的速度分布与自弯曲曲率半径的关系;以板材自弯曲成形为例,设计适用于板材自弯曲成形的挤压模具,利用数值模拟手段,分析自弯曲挤压的金属流动过程与成形机理;利用响应面模型结合粒子群算法,研究自弯曲挤压成形工艺的优化设计方法;通过工业级实验制备出自弯曲铝合金板型材,验证了模具结构的可行性与预测模型的可靠性。
1 板材自弯曲变形过程的数学模型
型材在模具出口处的挤出速度分布决定了挤出型材的形状,所以挤出速度分布与型材的弯曲变形存在确定的函数关系;当挤压模具能稳定挤出标准弯曲型材时,挤出速度分布是如何分布的?针对这一问题通过连续介质力学可以得到解决。
通常在研究金属的塑性变形时,体积力与面力相比可以忽略不计,对于挤压自弯曲工艺,金属挤出后在型材厚度方向无应力作用,所以,铝合金板材挤出自弯曲变形过程属于平面应力问题。

图1 圆柱坐标系下型材上微元体的受力图
Fig. 1 Stress diagram of the micro-element on profile in cylindrical coordinate system
如图1所示,在圆柱坐标系下,挤出型材上微元体的应力张量为: ,应变率张量为:
,应变率张量为: ,速度为
,速度为 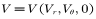 。
。
对微元体的动量方程为:
 (1)
(1)
 (2)
(2)
连续性方程为:
 (3)
(3)
应变率的几何方程为:
 (4)
(4)
 (5)
(5)
 (6)
(6)
其中 。
。
材料在塑性变形时,其应变速率和流变应力之间可用双曲正弦函数式的 Arrhenius 方程描述:
 (7)
(7)
式中,n为应力指数,Q为激活能,R为理想气体常数,A和α 为与材料相关的常数在稳定挤出标椎圆弧型材后,型材上质点的速度不再变化且沿着弯曲方向,所以,型材上质点的物质导数 ,径向速度
,径向速度 ,将此边界条件带入式(3),(4),(5)得到
,将此边界条件带入式(3),(4),(5)得到


由此可以知道,挤压稳定后型材在不同径向截面上质点的速度分布不变;然后由式(7)得
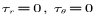
将此条件与 ,代入式(1),(2),(7)得:
,代入式(1),(2),(7)得:

代入式(6)得:
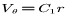 (8)
(8)
其中C1是常数
由式(8)可以看出,理想圆弧型材稳定自弯曲挤出时,型材径向质点的速度分布是线性的。这类似于刚体的圆周运动。在不同的径向截面上,保证相同的截面形状。

图2 板材理想自弯曲挤出的模具出口速度分布
Fig. 2 Die outlet velocity distribution of ideal Self-bending extrusion forming of sheet profile
如图2所示,模具的出口速度分布是线性的,挤出型材内部的曲率半径为 R,型材内轮廓的挤压速度为Vinside,型材外轮廓的挤出速度为Voutside,型材的宽度为d,所以出口速度分布的斜率即为:

由同时性得:

所以得:
 (9)
(9)
式 (9)说明型材的自弯曲半径的大小,受出口速度的均值和速度分布斜率的影响。挤出速度不均匀程度相同时,挤压比越大,即出口速度的均值越大,自弯曲半径越大;挤压比一定时,出口速度分布斜率越小,自弯曲半径越大,但在一定的模具结构条件下,挤出速度均值与速度分布的不均匀性存在耦合关系,挤压速度越大,挤压速度的不均匀性越大,速度分布的斜率越大,所以,自弯曲曲率半径的大小需要从两方面综合考虑。同时出口速度分布的线性程度影响弯曲的精度,线性程度越高,型材的弯曲变形越接近标准圆弧。
2 板材自弯曲挤压成形模拟与分析
2.1 板材自弯曲挤压模具设计及有限元模型建立
本模拟以截面 L80mm×t8mm(其中 L 表示宽度,t 表示厚度)的板材为研究对象,如图3所示为板材自弯曲挤压模具结构。图3(a)所示为模具导流腔结构图,上下两侧轮廓呈一定倾斜角度α,在这里α=9.6°,挤压比λ=20.7,轮廓偏置厚度t=5.5mm,窄端宽度d=20mm;图3(b)所示为整个挤压模具,包括导流板与挤压模。自弯曲挤压成形的有限元模型如图4所示,其中挤压杆、挤压筒、导流板、挤压模设置为刚体,坯料设置为塑性体,采用绝对网格控制法,在材料可能发生大变形的区域进行网格细化控制;坯料选用直径为120 mm的AA6063铝合金棒材,坯料预热温度为480℃,AA6063铝合金的应力应变本构关系参照文献[15]中的实验数据,坯料与模具间采用剪切摩擦模型,摩擦因子设置为0.7,坯料与工作带间采用库伦摩擦模型,摩擦因子设为0.3[15-19],具体挤压工艺参数如表1所示。

图3 板材自弯曲挤压模具结构图
Fig.3 Structure of self bending extrusion die for sheet profile
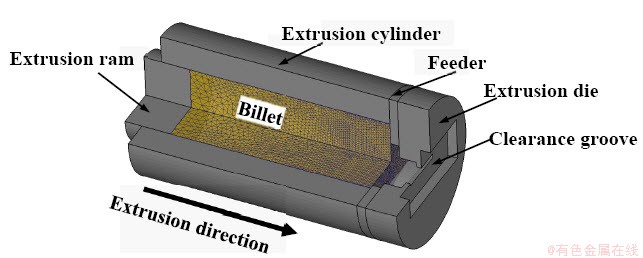
图4 板材自弯曲挤压过程有限元模型
Fig.4 Finite element model of self bending extrusion of sheet profile
表1 挤压工艺参数
Table 1 Extrusion process parameters

2.2 板材自弯曲挤压过程金属流动分析
通过有限元法计算后,不同挤压阶段的金属流动行为如图5所示。整个自弯曲挤压变形过程,在挤压杆的作用下,坯料被压入模具,开始填充模腔,如图5(a)所示,由于导流腔两端截面积存在差异,宽口侧金属流入量大,导致导流腔内材料质点的流动速度不均匀,宽口轮廓对应的模具出口速度较大,由于金属的变形协调作用,挤出的板型材向速度慢的一侧自然弯曲成形,如图5(b)所示,随着挤压行程的增加,模具出口速度分布已达到稳定状态,型材开始稳定挤出,进入挤压稳定阶段,如图5(c)~(d)所示,测得弯曲半径为177.5mm。

图5 板材挤压自弯曲变形过程
Fig.5 Extrusion self bending process of sheet profile
如图6所示为挤出型材的速度分布与流线分布,稳定挤出后弯曲型材上速度分布如图6(a)所示,可以看出模具出口处的速度呈高度线性分布,拟合得到速度分布斜率K=0.129,由式(9)得R=165.9mm,与测量得到的弯曲半径相对误差为6.54%,说明预测式(9)较为可靠;出口速度的高度线性分布主要由模具结构所致,且金属的变形协调性也能促进金属由不均匀流动到速度线性分布的作用,所以自弯曲模具结构的设计具有一定的“设计弹性”。挤出稳定后材料的流线如图6(b)所示,可以看出弯曲型材上的周向流线接近平行,除型材两端部分流线较密集,其他大部分流线间隔几乎相等,说明型材可以稳定挤出圆弧型型材而没有扭曲变形;由弯曲型材上的径向流线的突起峰略偏外侧,由此可知坯锭金属流向弯曲外侧比内侧多。

图6 挤出型材的速度分布与流线分布
Fig.6 Velocity distribution and streamline distribution of extruded profiles
2.3 板材自弯曲成形机理分析
图7(a)~(b)与图8为不同型材挤出时刻的应变速率云图,本文以应变率为0.001/s为界判定是否有塑性变形,进而分析板材自弯曲挤出成形的机理。
挤压初期由于自弯曲挤压模具结构的特点,型材挤出速度分布不均匀,型材刚挤出后受内部剪切应力作用发生协调变形,形状向速度相对较小一侧弯曲,如图7(a)所示,整个挤出型材在发生协调变形,在变形过程中内部剪切应力也随之削弱;随着型材不断挤出并弯曲变形,如图8(a)~(c)所示;挤出一段时间后,型材的内应力消减至不足以发生剪切变形,型材截面速度不再发生变化,此段型材不再发生内部金属的协调变形,协调变形区迅速缩减至模具出口后一段距离,如图7(b)所示,挤压进入稳定阶段,此后型材挤出总是由后面的金属推动前面,发生刚性平移,如图7(c)所示为Avrami模型所得到的挤压件残余应变的中剖面图,削弱后的内应力以残余应力的形式储存在前段型材中。
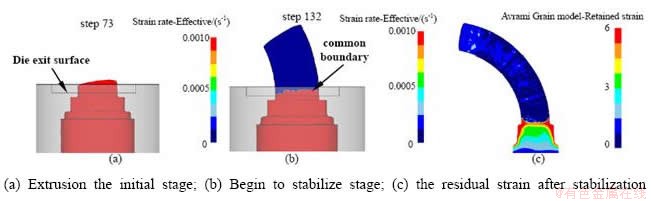
图7 挤压的不同阶段与残余应变
Fig. 7 Different stages of extrusion and residual strain
因模具出口处金属流速的不均匀性产生的内应力足以发生协调变形,而前段已变形完的型材又不再发生塑性变形,只做刚性移动,所以,在模具出口与不变形段型材之间存在一个变形区与非变形区的交界,在模具出口到此交界处为变形协调区,此交界前段为刚性移动区,如图7(b)所示,此交界大致在模具出口挤出后一小段距离上,随挤压的进行,协调变形区保持相对稳定,与非变形区的交界面在挤压过程中波动较小,型材的挤出较为稳定,如图8(d)~(f)所示。
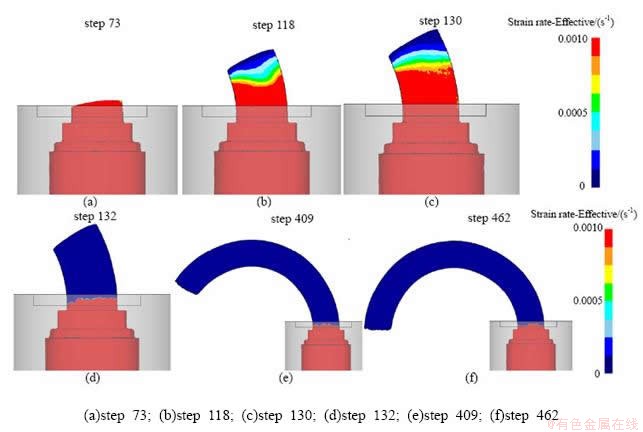
图8 整个板材自弯曲挤压成形过程
Fig. 8 The process of self bending extrusion of sheet profile
3 自弯曲挤压模具结构优化设计
3.1 拉丁超立方法试验设计
现自弯曲挤压模具的设计,多用于定性分析工艺的可行性,通过指定型材弯曲半径进行逆向设计自弯曲挤压模具结构的研究较少,本文将优化算法应用于自弯曲挤压成形的工艺优化设计,通过指定型材弯曲半径利用上文中的数学模型,优化模具结构参数。
式(9)已经建立了弯曲半径与出口速度分布参量的关系,而且其预测效果也较为可靠,所以,式(9)可以作为自弯曲模具设计的目标函数;由式(9)和板材自弯曲成形机理可知,只需由挤压稳定时的出口速度分布,即可预测型材的自弯曲曲率半径,而挤压大变形数值模拟算法中,有限体积法多用于求解挤压稳态过程,其求解计算效率比有限元法提高至少3倍[20-22],所以,在模具优化设计中可以采用有限体积法进行数值模拟[23],再进一步通过式(9)做出预测,进而缩短研发周期。
表2 优化变量与取值范围
Table 2 Optimized variables and value range

本文以弯曲半径1900mm的板材为优化目标,结合响应面模型,对模具结构与挤压速度的优化设计,提取模具结构因子α、d与挤压速度v作为优化变量,其他模具尺寸按图3设计,试验所选因素与取值范围如表2所示;通过设计拉丁超立方随机抽样[24-25]程序,得到20组模拟试验方案,计算挤压稳态过程,得到各组试验下的仿真结果,如表3所示,各组模具出口处金属的挤出速度分布如图9所示。
表3 模拟试验结果表
Table 3 simulation test results


图9 各抽样试验的模具出口速度分布
Fig. 9 Velocity distribution ofextrusiondie exit in sampling test
3.2 响应面结合粒子群算法优化
选择二阶响应曲面方程来预测不同设计变量组合下的响应值,利用最小二乘法进行参数拟合,由表3的仿真试验数据得到的响应面函数为
 (10)
(10)
定义模型的决定系数β为:

式中, 为响应面模型的预测值,
为响应面模型的预测值, 为表3中的弯曲半径值,
为表3中的弯曲半径值, 为表3中的弯曲半径值的平均值;决定系数β的大小能反应响应面模型对试验观测值的拟合程度,β的取值范围为[0,1];β的值越接近1,说明响应面模型的拟合程度越好。经计算模型决定系数β=0.95,说明该响应面模型具有较好的预测效果,可用于预测与优化。
为表3中的弯曲半径值的平均值;决定系数β的大小能反应响应面模型对试验观测值的拟合程度,β的取值范围为[0,1];β的值越接近1,说明响应面模型的拟合程度越好。经计算模型决定系数β=0.95,说明该响应面模型具有较好的预测效果,可用于预测与优化。

图10 变量与板材弯曲半径的响应面
Fig. 10 Response surface of variable and sheet bending radius
各变量对板材弯曲半径响应面模型的三维曲面图,如图10所示;由图10(a)可知,板材的弯曲半径随窄端宽度d的增大而增大,随轮廓倾斜角α的增大而减小,这是因为窄端宽度d的减小和轮廓倾斜角α的增大均会增大金属流动的不均匀性,导致挤出速度分布梯度大,进而板材弯曲会减小;由图10(b)可知,当窄端宽度d较大时,板材弯曲半径R随挤压速度v的增大而增大,当窄端宽度d较小时,挤压速度v对板材弯曲半径R无显著影响,虽然增大窄端宽度d会减小金属流动的不均匀性,使弯曲半径增大,但挤压速度的增加又会增大金属流动流动的不均匀性,同时由式(9)可知,平均挤出速度的大小也对型材的自弯曲半径有影响,所以,三种因素的相互作用决定了板材弯曲半径的大小。
采用粒子群优化算法[26]对所建立的响应面模型进行快速寻优,当板材的目标弯曲半径为1900mm时,板材弯曲半径容差范围定为(1900,1905),将该约束条件以罚函数形式加到目标函数后面,使最优解限定于(1900,1905)区间内。本次优化迭代,设置初始种群粒子数为30个,学习因子为1.2,最大迭代次数为200次。进化迭代次数与适应度值之间的关系如图11所示,迭代67次后粒子达到最佳位置。得到最优参数组合为轮廓倾斜角α=5.02°,窄端宽度d=30.55mm,挤压速度v=3.69mm/s,最优解为R=1900mm。

图11 优化迭代曲线
Fig. 11 Optimize iteration curve
3.3试模实验与金相组织观察
对优化之后的模具结构与挤压速度的最优参数组合,设计自弯曲挤压模具,并进行加工试模,所得工业级挤压模具如图12所示;挤压铝锭的材料与尺寸、挤压温度参照表1列出的数值,对铝锭预热3小时后,采用1000 T正向单动挤压机进行挤压试模实验,如图13所示,可以看出在挤压过程稳定后,挤出的板材能够发生稳定的自弯曲变形,得到板材的弯曲曲率半径为2071mm,与响应面模型的预测值相差8.25%,说明该响应面预测模型较为可靠。

图12 板材自弯曲挤压实验模具
Fig. 12 Experimental die for sheet profileself bending extrusion
对挤出后的弯曲板材宽面的内外两侧进行金相组织观察,采用电解抛光同时附加超声波震动的方法,抛光液为15%的高氯酸与无水乙醇的混合溶液,体积比为10 ml:50 ml,直流电压为5 V,抛光时间为1 min,采用 IE200M 型光学显微镜进行微观组织观察,利用平均截线法多视场表征挤出方管弯曲件的平均晶粒尺寸s(s=1.74y,y为截线长度)[11],直接得到如图14所示的金相组织,由图14可知,内外两侧均为等轴晶组织,外侧板材晶粒大小为85μm左右,内侧板材晶粒大小为75μm左右,可以看出晶粒组织尺寸略微偏大,这可能是由于挤压温度过高和未及时冷却的原因所造成的。

图13 工业级挤压试验获得的弯曲板材。
Fig.13 Bending profile obtained by industrial grade extrusion experiment.

图14 板材内外侧金相组织
Fig.14 Metallographic structure of inner and outer sides of sheet profile
4 结论
1) 对于型材自弯曲挤压成形工艺,挤出型材的弯曲半径与出口速度存在一一对应的关系,通过连续介质力学,可推导出理想自弯曲挤出型材的曲率半径与挤出速度分布的函数关系,即 。
。
2) 通过基于异形导流腔结构,提出了一种板材自弯曲挤压成形工艺,得到自弯曲挤出成形的板材;型材刚挤出时,整个挤出型材在发生协调变形,挤压稳定后协调变形区迅速缩减至模具出口后一段距离,型材大部分不再发生塑性变形,变形区与非变形区的交界在模具出口后一小段距离上,并随挤压的进行交界面略有波动,且挤出的型材附带残余应力。
3) 带罚函数形式的目标函数,结合响应面模型与粒子群算法,可用于型材自弯曲挤压成形的优化设计;通过工业级挤压实验,得到了弯曲板材,板材在挤出后发生稳定自弯曲,挤出型材组织均匀,为自弯曲模具的研发设计提供理论与技术参考。
REFERENCES
[1] 刘志文,李落星.轻量化构件弯曲短流程工艺研究现状与进展[J].中国有色金属学报,2014,24(08):2003-2012.
LIU Zhi-wen LI Luo-xing.Review of bending short process for lightweight component[J]. Transactions of Nonferrous Metals Society of China,2014,24(08):2003-2012.
[2] ZHAI R X, DING X H, YU S M, WANG C G,Stretch bending and springback of profile in the loading method of prebending and tension[J].International Journal of Mechanical Sciences,2018,144:746-764.
[3] 张弥,王晓东,苏亚东,关志东.钛合金点阵夹芯结构弯曲性能[J].中国有色金属学报,2018,28(03):457-464.
ZHANG Mi, WANG Xiao-dong, SU Ya-dong, GUAN Zhi-dong.Bending behavior of titanium truss core sandwich structure[J]. Transactions of Nonferrous Metals Society of China,2018,28(03):457-464.
[4] 陈清根,徐雪峰,马媛媛,李玲玲,赵爽,徐龙.采用小弯曲半径弯头反向推直与正向推弯的管坯设计方法[J].中国机械工程,2017,28(03):353-358.
CHEN Qing-gen, XU Xue-feng, MA Yuan-yuan, LI Ling-ling, ZHAO Shuang, XU Long. Tube Design Method with Small Bend Radius in Elbow Forming Using Reverse Push Straight and Forward Forming Simulation[J].China Mechanicalengineering,2017,28(03):353-358.
[5] 朱英霞,刘郁丽,杨合,李海平.压块对H96矩形管绕弯成形回弹与截面变形的作用[J].中国有色金属学报,2014,24(01):104-114.
ZHU Ying-xia, LIU Yu-li, YANG He, LI Hai-ping.Impact of pressure die on springback and section deformation of rotary-draw bending of rectangular H96 tube [J]. Transactions of Nonferrous Metals Society of China,2014,24(01):104-114.
[6] YANG H, LI H, ZHANG Z Y, ZHANG M, LIU J, LI G J. Advances and Trends on Tube Bending Forming Technologies[J]. Chinese Journal of Aeronautics, 2012, 25(1): 1-12.
[7] 张弥,王晓东,苏亚东,关志东.钛合金点阵夹芯结构弯曲性能[J].中国有色金属学报,2018,28(03):457-464.
ZHANG Mi, WANG Xiao-dong, SU Ya-dong, GUAN Zhi-dong. Bending behavior of titanium truss core sandwich structure[J].The Chinese Journal of Nonferrous Metals,2018,28(03):457-464.
[8] KLEINER M,ARENDES D.The manufacture of non-linear aluminum sections applying a combination of extrusion andcurving[J].Advanced Technology of Plasticity,1996,(2):971-983.
[9] KLAUS B. MüLLER. Bending of Extruded Profiles during Extrusion Process[J]. International Journal of Machine Tools and Manufacture, 2006, 46(11): 1238-1242.
[10] SHIRAISHI M, NIKAWA M, GOTO Y. An investigation of the curvature of bars and tubes extruded through inclined dies[J]. International Journal of Machine Tools and Manufacture, 2003, 43(15):1571-1578.
[11] CHEN FK, CHUANG WC, SHAN T. Finite element analysis of multi-hole extrusion of aluminium alloy tubes[J]. Journal of materials processing technology. 2008, 201:150-155.
[12] 石磊,徐国辉,任畅,金文中,王玉江,王利剑. 动态流量控制法挤出镁合金三维弯曲管件[J]. 材料科学与工艺, 2016, (6): 8-13.
SHI Lei, XU Guo-hui, REN Chang, JIN Wen-zhong, WANG Yu-jiang, WANG Li-jian. Three dimensional magnesium alloy bent pipe produced by dynamic flow control extrusion[J].Materials Science and Technology,2016, (6): 8-13.
[13] 石磊,文九巴,姚怀,贺俊光,吴武伟,廖桂华.钛合金弯管动态流量控制法挤压成形的模拟与实验研究[J].中国有色金属学报,2019,29(02):380-387.
SHI Lei, WEN Jiu-ba, YAO Huai, HE Jun-guang, WU Wu-wei, LIAO Gui-hua.Numerical simulation and experimental study of titanium alloy bending tube extruded by dynamic flow control technique[J]. 2019,29(02):380-387.
[14] ZHOU W B, LIN J G, TREVOR A. DEAN, WANG L L. Feasibility studies of a novel extrusion process for curved profiles: Experimentation and modelling[J]. International Journal of Machine Tools and Manufacture,2018, 126: 27–43.
[15] YU J Q, ZHAO G Q, CHEN L. Analysis of longitudinal weld seam defects and investigation of solid- state bonding criteria in porthole die extrusion process of aluminum alloy profiles [J]. Journal of Materials processing Technology, 2016, 237: 31-47.
[16] JIE Y I, WANG Z H, LIU Z W, ZHANG J M,HE X. FE analysis of extrusion defect and optimization of metal flow in porthole die for complex hollow aluminiumprofile[J]. The Chinese Journal of Nonferrous Metals, 2018, 28: 2094-2101.
[17] 黄东男,李静媛,张志豪,谢建新. 方形管分流模双孔挤压过程中金属的流动行为[J]. 中国有色金属学报, 2010, 20(3):488-495.
HUANG Dong-nan, LI Jing-yuan, ZHANG Zhi-hao, XIE Jian-xin. Metal flowing behaviors during diplopore extrusion of square tube with porthole die[J]. The Chinese Journal of Nonferrous Metals,2010, 20(3):488-495.
[18] 王晓溪,张翔,金旭晨,黄传辉,何敏.新型等通道球形转角膨胀挤压过程模拟与实验验证[J].中国有色金属学报,2018,28(11):2281-2287.
WANG Xiao-xi, ZHANG Xiang,JIN Xu-chen, HUANG Chuan-hui, HE Min. Simulation and experimental validations of novel process entitled equal channel angular expansion extrusion with spherical cavity[J].The Chinese Journal of Nonferrous Metals,2018,28(11):2281-2287.
[19] 王晓溪,张翔,张磊,金旭晨,韩颢源.工业纯铝等通道球形转角挤压数值模拟与实验研究[J].中国有色金属学报,2019,29(07):1360-1366.
WANG Xiao-xi, ZHANG Xiang, ZHANG Lei, JIN Xu-chen, HAN Hao-yuan.Numerical simulation and experimental investigation of commercially pure aluminum during equal channel angular extrusion with spherical cavity[J].The Chinese Journal of Nonferrous Metals, 2019,29(07):1360-1366.
[20] LI X R, FANG W L, TANG D, QIAO Y,SUN Y L,LI D Y. Numerical simulation on hot extrusion forming of aluminum alloy micro-multiport profile[J]. Journal of Plasticity Engineering, 2017, 24(5):1-6 and 31.
[21] BRESSAN J D , MARTINS M M , BUTTON S T. Analysis of Aluminium Hot Extrusion by Finite Volume Method[J]. Materials Today Proceedings, 2015, 2(10):4740-4747.
[22] 张侠,钱进浩,龚小涛,成国发,於孝谦.6061铝合金灯具散热底座芯轴挤压成形研究[J].锻压技术,2020,45(01):125-130.
ZHANG Xia, QIAN Jin-hao,GONG Xiao-tao, CHENG Guo-fa,YU Xiao-qian. Research on extrusion forming of 6061 aluminum alloy spindle for lamp cooling holder[J]. Forging and Stamping Technology,2020,45(01):125-130.
[23] MARTINSM, BRESSANJ, BANDINIC.Validation of Finite Volume Method by hot extrusion analysis of aluminium alloy[J],Materials today: proceedings,2019,10:234.
[24] FANG WL, TANG D, WANG H M, LI D Y, PENG YH,Optimization of die design for thin-walled flat multi-port tube with the aid of finite element simulation[J].Journal of Materials Processing Technology,2019,116418.
[25] KEVIN B, PAMELA B, DIANE D, BEVAN T,Populations of Models, Experimental Designs and Coverage of Parameter Space by Latin Hypercube and Orthogonal Sampling[J].Procedia Computer Science,2015(51):1762-1771.
[26] 任助理,王李管,贾明涛.基于粒子群优化算法和ANFIS的矿体品位插值[J].中国有色金属学报,2019,29(01):194-202.
REN Zhu-liWANG Li-guanJIA Ming-tao.Grade interpolation of orebody based on particle swarm optimization algorithm and ANFIS [J].The Chinese Journal of Nonferrous Metals,2019,29(01):194-202.
The Forming Mechanism of Extrusion Self Bendingof Aluminum Alloy Sheet Profile and Optimum Design of Die
MIN Fan-lei,ZHU Guang-ming, GAO Xu-jie,YUE Bo-wen,LIU Hui-ping,GUO Na-na,ZHAI Xiao-qing
(School of Mechanical Engineering, Shandong University of Technology, Zibo 255000,China)
Abstract:Based on the theory of continuum mechanics, the relationship between the exit velocity distribution and the radius of curvature of the plate during the ideal self-bending process is obtained. A new process for the self-bending extrusion of aluminum alloy plates is proposed. By designing the structure of special-shaped guide cavity, the uneven flow of metal in the die cavity is produced, so the curved profile is directly extruded; By using numerical simulation, the self bending deformation mechanism, metal flow characteristics and distribution of residual strain in the process of sheet profile extrusion are analyzed. The response surface prediction model of each variable to the radius of curvature of extrusion self bending is established by using the Latin hypercube sampling method and the finite volume method. Under the condition of a specified bending radius of 1900 mm, an objective function optimization model with a penalty function was established. The algorithm obtains the optimal cavity structure and process parameters, and conducts trial experiments. The experimental results show that the self-bending sheet extrusion is stable, the measured radius of curvature is 2071 mm, the grain size inside and outside of the curved sheet is uniform.
Key words:Aluminum alloy bending sheet profile; self bending forming; relation derivation; mechanism analysis; optimal design
Foundation item:Project(ZR2017MEE036) supported by Natural Science Foundation of ShandongProvince; Project(ZR2017BEM003) supported byPh.D. Programs Foundation of Natural Science Foundation of Shandong Province;Project (2017ZBXC205) supported by Zibo City School City Integration Development
Received date: 2019-00-00; Accepted date: 2019-00-00
Corresponding author:ZHU Guang-ming(1976—),Tel: 13853329826; E-mail: zgm@sdut.edu.cn
基金项目:山东省自然科学基金(ZR2017MEE036);山东省自然科学基金博士基金(ZR2017BEM003);淄博市校城融合发展计划项目(2017ZBXC205)
收稿日期:20**-**-**;修订日期:20**-**-**
通讯作者:朱光明(1976—),男,教授,博士;电话:13853329826;E-mail: zgm@sdut.edu.cn