DOI: 10.11817/j.issn.1672-7207.2016.03.045

高含水率条件下压实黏性土路基永久变形

过震文^{1, 2}，钱劲松³

(1. 长沙理工大学 交通运输工程学院，湖南 长沙，410114；

2. 上海市市政规划设计研究院，上海，200031；

3. 同济大学 教育部道路与交通工程重点实验室，上海，200092)

摘要：对上海地区3条公路的黏性路基土样进行室内动三轴重复加载试验，以考察潮湿多雨、高地下水位地区黏性土路基高含水率(通常大于最佳含水率)状态对其永久变形特征的影响。研究结果表明：含水率的较小幅度变化可引起黏性土永久变形成倍增加；Chai-Muria模型的拟合曲线表现出与试验值非常高的一致性，R²均保持在0.90以上，均大于Tseng-Lytton模型的拟合接近程度；使用路基土基本物性指标对Chai-Muria模型中的参数进行了回归分析，具有较好的预估效果。

关键词：路基工程；永久变形；高含水率；预估模型

中图分类号：V416.1          文献标志码：A         文章编号：1672-7207(2016)03-1058-07

Permanent deformation of compacted clay with high moisture content

GUO Zhenwen^{1, 2}, QIAN Jinsong³

(1. School of Transportation Engineering, Changsha University of Science &Technology, Changsha 410114, China;

2. Shanghai Municipal Planning Design Research Institute, Shanghai 200031, China;

3. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University,

Shanghai 201804, China)

Abstract: To explore and predict the influence of water content, especially high water content( above optimum moisture content), on the permanent deformation of compacted clay, a series of repeated load dynamic triaxial (RLT) tests were conducted on three kinds of soils in Shanghai. The experimental results reveal that the tested subgrade soils are extremely sensitive to moisture content. Curve fitting based on Chai-Muria model shows very high consistency with the test results and R² are kept above 0.9, which is greater than that of Tseng-Lytton model. The model with parameters obtained by regression analysis based on soil properties has good result in prediction.

Key words: subgrade engineering; permanent deformation; high moisture content; prediction model

路基的动力变形对于含水率的变化非常敏感^[1]。潮湿多雨地区，在最佳含水率(C_OM)附近压实的黏土路基，湿度在公路投入运营后会不断变化，一般在2~3 a内达到平衡，即平衡含水率(C_EM)，并且普遍高于最佳含水率。在高湿度与交通荷载附加应力耦合作用下，路基性能明显下降^[2]，可能会发生过量的动力变形，从而产生严重的路面病害，如车辙、裂缝、沉降、不协调变形等。通过室内动三轴试验并由此建立预估模型是研究路基土动力永久变形的重要手段，而室内试验中含水率的控制条件是决定永久变形模型适用范围和预估精度的关键之一。目前，现有研究多集中于含水率处于C_OM附近的非饱和土，对由于高地下水位引起的高湿度乃至近饱和状态考虑得不多^[3-8]。例如，UZAN^[3]选择塑限的1.22 倍，MUHANNA等^[4]选择C_OM与C_OM±2.5%。在此，本文作者通过室内重复动三轴实验，研究了高含水率条件下黏性土路基的永久变形特征，并比较了既有典型预估模型的拟合效率。

1  室内重复加载动三轴试验

1.1  土样物性参数

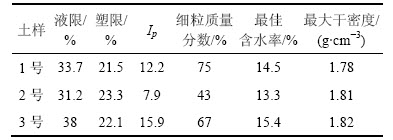
试验选取的1~3号土样分别取自上海绕城高速、曹安公路和崇启高速路段，1~3号土样的基本物性参数如表1所示。

表1  土样基本物性参数

Table 1  Basic material properties of soil samples

1.2  实验方案

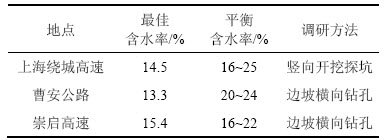
为确定试验中的含水率范围，针对以上3个路段进行了现场湿度调研，结果如表2所示。滨海地区地下水位高，一般为0.5~1.0 m，对路基内部湿度的空间分布特征起决定性作用，所调研路段的黏性土路基平衡含水率均大于最佳含水率，并可在最佳含水率基础上最大提升超过10%。

表2  现场湿度调研

Table 2  Result of field moisture observation

含水率根据上述现场调研情况选择最佳含水率附近(14%)与平衡含水率(22%)附近，压实度取90%与96% 2种情况。而对于路基土在受到不同交通荷载作用下的动应力、静应力、围压，可通过BISAR软件计算得到。综上制定试验方案如表3所示。此外，本试验设备采用UTM-100系统，波形为半正弦波，荷载频率为1 Hz，加载时间为0.2 s，荷载间歇时间为0.8 s。考虑误差的控制，分别对每种工况下的土样至少制备3个平行试件进行试验。

1.3  高含水率试件制备

在室内动三轴试验过程中，试件的属性(例如含水率和压实度等)直接影响试验数据的有效性与可靠性，因此制备出形状规则、属性符合试验条件的试件非常重要。一般情况下，试件可通过直接静压成型的方法制备；当土样的含水率较高时，试件在静压成型的过程中内部的水分因受到强大的挤压而流出模具，从而导致制成的试件不能达到目标含水率。

表3  室内动三轴试验方案

Table 3  Experimental scheme of dynamic triaxial test

为了解决上述问题，高含水率试件的制备使用如图1(a)所示方法^[9]：1) 先将试件在最佳含水率状态下成型，脱模后在上下两侧同时垫好滤纸与透水石；2) 用双层橡皮膜进行包装，在试件上方形成一定空间，同时在透水石位置放置橡皮筋以防止水从侧面下渗；3) 再加入由最佳含水率情况下达到目标含水率时所需的水，最后放入到密封的养生箱，待试件内的水分均匀分布。该方法各构件取用方便、可操作性强、实用效果明显。

为了确定试件养生的时间，即掌握试件内部的含水率何时达到平衡，采用以下的方法对渗水的试件进行观测：包装好的试件同时加水放入养生箱，每24 h从养生箱内取出1个试件，在高度方向从下而上分成6个部分进行含水率的测试。图1(b)所示为目标含水率为22%试件在养生过程中含水率变化规律：加水初期试件最大、最小含水率差为5.5%，静置时间满7 d后，试件最大、最小含水率差稳定在1.5%附近。当继续增加静置时间至8~10 d时，含水率差变化不明显。故建议含水率由C_OM增大至C_EM时，吸水静置时间控制在7 d。

图1  高含水率试件制备方法

Fig. 1  Preparation of specimen with high moisture content

1.4  试验误差控制

高含水率试件制备的困难和目标含水率的试验控制误差可能增加试验数据的误差和离散性，为尽量减少这一影响，对每种工况的3个试件，要求永久变形测试值的最大相对误差(Δ_max)不超过5%；若超出范围则该结果无效，需要重新进行试验。最终各工况下测试数据的最大相对误差如图2所示，满足控制要求。

图2  试验结果误差

Fig. 2  Error analysis of test results

2  试验结果分析

2.1  试验数据处理

如图3(a)所示，在半对数坐标下永久变形分为前后2个阶段(加载数N=100次左右)，2个阶段中基本上呈线性关系，造成这种特征的主要原因很可能来自于各试件之间及试件本身属性的不稳定(比如高含水率试件制备过程中的因膨胀引起的压实度变化等)，使得动力应变在荷载作用初期规律不均匀。随着加载次数的增加，动力应变累积规律越趋于稳定。

对于实际路基中的土样而言，通常这种初期变形规律变异性较大的阶段在施工过程中就会完成，在处于实际运营期的路基中并不会发生。因此，可采用以下的方法对各工况动力变形试验初始数据作处理：基于后段直线的斜率对前面不稳定的数据进行插值并覆盖，然后再基于插值后的第1个数据(N=1)，整体上下平移所有的数据，使初始值为0，如图3(b)所示。

2.2  含水率对黏土永久变形的影响

为更好地研究含水率对路基动力变形的影响，可以在其他条件均相同的情况下分别对3种土进行分析。以工况B2和D2为例说明，如图4所示。含水率由14%增至22%时，3种土的动力应变分别由0.165%增至1.614%、0.113%增至1.570%、0.142%增至0.736%，分别增加至9.8倍、13.9倍、5.2倍。结果说明含水率对黏性土永久变形有显著影响。

动力变形随含水率提升而显著增大，主要可归结于2个方面的原因。其一，粒径较小的黏土颗粒表面的结合水膜厚度增大，颗粒间斥力增大而引力相对减小，致使黏粒比较容易克服相互之间的引力，更易产生相互位移。其二，含水率继续增大后土中可能出现部分自由水，反复加载后孔隙中过多的水分不易立即排出，形成一定的超孔隙水压力，降低土体整体强度和抗变形能力。

由于道路运营过程中黏性土路基中的平衡含水率远高于其最佳含水率，而含水率的较小幅度变化可引起黏性土永久变形成倍增加，故进行路基长期性能研究时，应选用能反映这一现象的永久变形预估模型。

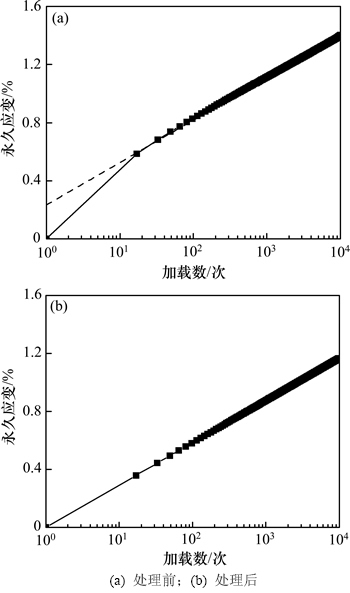
图3  动力变形实验数据处理

Fig. 3  Data processing of permanent deformation experiment

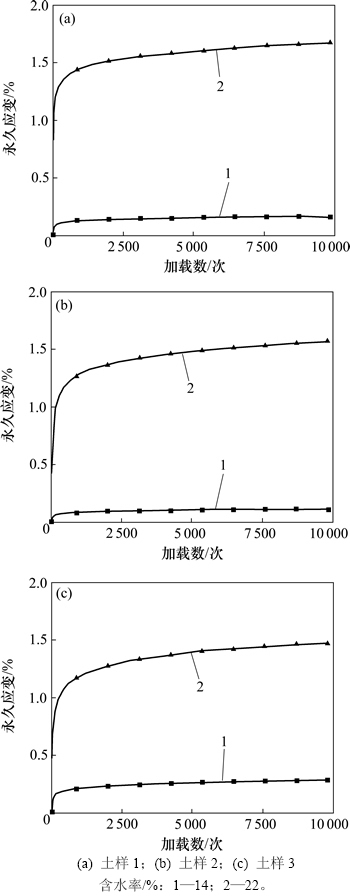
图4  含水率对永久变形的影响(工况B2和D2下)

Fig. 4  Effect of moisture content on permanent strain (under condition B2 and D2)

3  永久变形预估模型

3.1  现有永久变形预估模型

对重复动荷载作用下路基永久变形问题的研究，开创性的工作是Monismith对粉质黏土进行三轴重复加载试验，提出指数模型来预测路基土的永久变形：

                                     (1)

式中：ε_p为永久变形(又称塑性变形)；A和b为回归得到的材料参数。

LI等^[10]对式(1)进行改进，调整了参数A的表达，提出修正的累积塑性应变模型：

             (2)

式中：a和m为材料参数，表示土的类型的不同对累积塑性变形的影响；q_d为行车荷载引起的动偏应力；q_f为静力破坏偏应力。

SAMANG^[11]通过一系列室内动三轴试验研究累积塑性应变与初始静力偏应力的关系，发现二者之间有线性关系。CHAI等^[12]基于这一试验现象，对文献[10]的计算模型进一步修正，提出如下累积塑性应变计算公式：

         (3)

式中：a，m和b为材料参数，表示土的类型的不同对累积塑性变形的影响；参数n，一般取1.0；q_s为铺面结构荷载和路基自重荷载作用下的初始静力偏应力； q_f=2τ_f，由τ_f路基土抗剪强度指标计算。

该模型除了考虑动偏应力和静力破坏偏应力的影响外，还考虑了初始静力偏应力的影响，更适合于黏性路基土的累积塑性变形分析。

此外，Tseng-Lytton模型^[13]是常用的另一种形式的永久变形预估模型：

          (4)

式中：δ_a为各层的永久变形；ε₀，β，ρ为材料参数；ε_r为测定材料参数时所施加的回弹应变；ε_v为对多层体系进行力学分析得到的竖向应变；β_γ1为修正系数。

文献[14]中的永久变形预估模型即由该模型回归、简化得到。

3.2  永久变形模型选择与对比

Chai-Muria模型充分考虑了的材料参数和偏应力的影响，在该类模型中具有最好的预估效果。另外，目前国际上使用较广泛的AASHTO2002模型是简化自Tseng-Lytton 模型，可见Tseng-Lytton 模型总体上的预估效果已经得到了肯定。因此，本研究拟选取Tseng-Lytton模型和Chai-Muria模型，借助上述室内动三轴试验的数据，通过回归分析对2种模型的拟合效果进行验证。

模型回归分析过程中，绘制模型拟合曲线随N历时过程的变化规律，并与每个工况的实测值进行对比，如图5所示(以工况A1为例)，可见：对于Tseng-Lytton模型，虽然表现出了累积动力应变随着N变化的历时特征，但与实测值变化规律的吻合程度不良，当N＜2 000次时，拟合曲线以很快的变化速率达到一定的高度；随后(N＞2 000)动力应变的累积变化速率非常微弱，基本上呈水平趋势发展；同时，在5 000＜N＜10 000的范围内，3种不同的路基土各个工况的试验值均大于拟合值。而在该工况下，3种路基土基于Chai-Muria模型的拟合曲线则表现出与试验值非常高的一致性，R²均保持在0.90以上，均大于Tseng-Lytton模型的拟合接近程度。

图5  Tseng-Lytton模型与Chai-Miura模型的对比

Fig. 5  Comparison of Tseng-Lytton model and Chai-Miura model

其他工况下的情况与上述相同，2种模型对于每种工况的回归拟合效果对比如图6所示。因此，选用Chai-Muria模型作为高湿度状态下黏性路基土动力应变预估模型更为合适。其原因在于Tseng-Lytton模型中包含了回弹应变，即假定在正常的路基工作状态下，可通过控制路基顶面回弹应变来控制永久变形，而在高湿度状态下，路基土的非线性特征更显著，这一假定可能不再适用；而Chai-Muria模型中包含了荷载应力与强度的比值，即考虑了实际应力水平对于路基力学性能的影响，可用于反映路基在高湿度状态下的非线性特征，故拟合效果更佳。

3.3  基于物性参数的永久变形预估方程

对Chai-Muria模型的参数进行多元线性回归，引入含水率、压实度、细粒质量分数、塑性指数等变量，建立模型参数与土样基本物性参数的经验回归关系，以实现由物性参数预估路基土的永久变形，更便于工程实际应用。回归结果如下：

lg(a)=0.310 740+0.011 019w-0.004 36R_c-0.004 36w_F+0.016 75I_p (R²=0.48)         (5)

lg(m)=1.066 707-0.009 13w-0.007 75R_c+0.001 14w_F-0.007 84I_p (R²=0.53)          (6)

lg(b)=-0.859 300-0.011 87w+0.000 96R_c+0.000 85w_F+0.003 85I_p (R²=0.65)      (7)

其中：w为含水率(%)；R_c为压实度(%)；w_F为细粒质量分数(%)；I_p为塑性指数(%)。

将试验方案中每个工况的条件代入到模型中，计算得到每种工况下的预估值，并与试验实测值进行对比，如图7所示。由图7可见：该模型在永久应变小于0.5%时的预估效果较好，大于0.5%时则存在较大的离散性。其原因存在于2个方面：一方面，试验仅包含了3种路基土和2种含水率条件，需要补充更多土样和更广泛含水率的试验样本，以提高其适用性和精度；另一方面，在高含水率条件下，土体的非线性特征非常显著，而试件制备及试验的困难均增加了试验数据的误差和离散性。尽管如此，在工程实践中，无条件进行重复动三轴试验时，本文提出的方法仍不失为预估永久变形的一个途径。

图6  Tseng-Lytton模型与Chai-Miura模型的对比

Fig. 6  Tseng-Lytton model versus Chai-Miura model

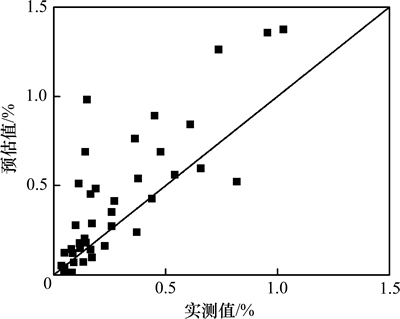
图7  实测值与预估值对比

Fig. 7  Comparison of measured and versus predicted values

4  结论

1) 黏性土路基中的平衡含水率远高于其最佳含水率，而含水率的较小幅度变化可引起黏性土永久变形成倍增加。

2) Tseng-Lytton模型假定可通过弹性变形预估永久变形，从而无法准确反映路基土在含水率较高时更明显的非线性特征，故选用考虑了应力水平的Chai-Muria模型作为高湿度黏性路基土动力应变预估模型更为合适。

3) 使用路基土的基本物性指标，对Chai-Muria模型中的参数进行回归得到永久变形预估方程。该模型在永久应变小于0.5%时的预估效果较好，可进一步丰富试验数据，同时在可能的情况下尽可能扩大试验中含水率的覆盖范围。

参考文献：

[1] 邱延峻, 孙振堂. 柔性路面路基土的永久变形[J]. 西南交通大学学报, 2000, 35(2): 116-120.

QIU Yanjun, SUN Zhentang. Permanent deformation of subgrade soils in flexible pavements[J]. Journal of Southwest Jiaotong University, 2000, 35(2): 116-120.

[2] 凌建明, 谢经保, 郑悦锋, 等. 基于地下水变位的路基顶面当量回弹模量预估[J]. 同济大学学报(自然科学版), 2005, 33(2): 162-165.

LING Jianming, XIE Jingbao, ZHENG Yuefeng, et al. Prediction method of equivalent resilient modulus on top of pavement subgrade with underground water table[J]. Journal of Tongji University (Natural Science), 2005, 33(2): 162-165.

[3] UZAN J. Characterization of clayey subgrade materials for mechanistic design of flexible pavements[J]. Transportation Research Record, 1998, 1629(1): 189-196.

[4] MUHANNA A S, RAHMAN M S, LAMBE P C. Model for resilient modulus and permanent strain of subgrade soils[J]. Transportation Research Record, 1998, 1619(1): 85-93.

[5] 杨树荣. 路基土壤反复载重下之回弹与塑性行为及模式建构[D]. 台北: 国立中央大学土木工程研究所, 2002: 55-57.

YANG Shurong. The resilient and plastic behavior of subgrade soils under repeated loading and its model development[D]. Taibei: National Central University. Department of Civil Engineering, 2002: 55-57.

[6] ZHAO Y S, DENNIS N D, ELLIOTT R P. Prediction of subgrade permanent strain using simple soil properties[J]. Geotechnical Engineering for Transportation Projects, 2004, 126(1): 1076-1085.

[7] 张洪亮, 郭忠印, 梁伟, 等. 粘土永久变形预估模型试验与仿真研究[J]. 西安建筑科技大学学报(自然科学版), 2009, 41(6): 764-770.

ZHANG Hong-liang, GUO Zhong-yin, LIA NG Wei, et al. Study on the permanent deformation prediction model of clay through tests and simulations[J]. Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2009, 41(6): 764-770.

[8] 冯怀平, 蒋闯. 水泥混凝土路面粉质粘土路基永久变形及其预测[J]. 路基工程, 2012(4): 170-173.

FENG Huaiping, JIANG Chuang. Prediction on permanent deformation of silty clay subgrade for cement concrete pavement[J]. Subgrade Engineering, 2012(4): 170-173.

[9] 李冬雪, 凌建明, 钱劲松, 等. 黏质路基土永久变形改进计算方法[J]. 同济大学学报(自然科学版), 2013(3): 386-389.

LI Dongxue, LING Jianming, QIAN Jinsong, et al. Improved calculation method of permanent deformation for cohesive subgrade soil[J]. Journal of Tongji University (Natural Science), 2013(3): 386-389.

[10] LI D, SELIG E T. Cumulative plastic deformation for fine-grained subgrade soils[J]. Journal of Geotechnical Engineering, 1996, 122(12): 1006-1013.

[11] SAMANG L. Settlement of soft deposit induced by cyclic loading[D]. Saga: Saga University. Department of Civil Engineering, 1997: 35-36.

[12] CHAI J C, MIURA N. Traffic-load-induced permanent deformation of road on soft subsoil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(11): 907-916.

[13] TSENG K H, LYTTON R L. Prediction of permanent deformation in flexible pavement materials[C]// SCHREUDERS H G. Implication of Aggregates in the Design, Construction, and Performance of Flexible Pavements. New Orleans: ASTM STP 1016, 1989: 154-172.

[14] Transportation Research Board of the National Academies. Guide for mechanistic-empirical design of new and rehabilitated structures NCHRP 1 -37A[R]. Washington D C: Transportation Research Board of the National Academies, 2004: 51-53.

(编辑  赵俊)

收稿日期：2015-03-06；修回日期：2015-06-18

基金项目(Foundation item)：国家自然科学基金资助项目(50908176)；交通运输部科技项目(2013319223010，2015318822170) (Project(50908176) supported by the National Natural Science Foundation of China; Projects(2013319223010, 2015318822170) supported by Science and Technology Program of Ministry of Transport of China)

通信作者：钱劲松，博士，副教授，从事道路工程研究；E-mail: qianjs@tongji.edu.cn