DOI: 10.11817/j.issn.1672-7207.2017.12.011

载重汽车用直齿轮冷挤压工艺参数多目标优化

梁强¹，周杰¹，何雄¹，夏泽雨²，刘正伟²

(1. 重庆大学 材料科学与工程学院，重庆，400044；

2. 重庆众联齿轮传动有限公司，重庆，402247)

摘要：针对大模数直齿轮冷挤压成形后端面加工余量大、齿顶塌角大和成形载荷大的问题，以齿顶圆角、入模角、劈分厚度、定径带长度为优化变量，应用响应面法和有限元数值模拟对齿轮冷挤压成形工艺参数进行多目标优化。以减小齿轮端面加工余量、提高齿顶充填性和降低成形载荷为目标，分别建立3个目标函数的二阶响应面模型，通过在可行变量空间内寻优，将优化后的最优工艺参数进行验证。研究结果表明：得到的模型预测精度高，能较好地描述3个目标函数关于设计变量的响应。大模数直齿轮冷挤压成形最优工艺参数为：齿顶圆角1.6 mm、入模角40°、劈分厚度2 mm、定径带长度15 mm。采用最优工艺参数加工的试样的端面加工余量降至1.91 mm，齿顶塌角量降至0.29 mm，成形载荷降低18.2%。工艺实验证明采用多目标优化得到的工艺参数可以获得合格的产品。

关键词：响应面法；大模数直齿轮；冷挤压；数值模拟

中图分类号：TG136             文献标志码：A         文章编号：1672-7207(2017)12-3216-08

Multi-objective optimization of cold extrusion process parameters for spur gear of camion

LIANG Qiang¹, ZHOU Jie¹, HE Xiong¹, XIA Zeyu², LIU Zhengwei²

(1. College of Material Science and Engineering, Chongqing University, Chongqing 400044, China;

2. Chongqing Zhonglian Gear Transmission Co. Ltd.，Chongqing 402247, China)

Abstract: Taking the defects such as large machining allowance of gear end-face, insufficient corner filling and large forming force in the process of cold extrusion of spur gear with large module as the research objects, the radius at tooth tip of die, die semi-angle, splitting thickness and length of die bearing were selected to be optimization variables. The response surface method (RSM) combined with finite element method (FEM) was used for the multi-objective optimization of cold extrusion process parameter. Aiming at reducing machining allowance, improving capacity of corner filling and lowering forming force, second-order response surface models of three objective functions were established based on the results of experiment design. The optimization graphs in the variable space were analyzed. The results show that the result models exhibit high prediction accuracy and can describe the response of the three functions on design variables accurately. The optimal process parameters are as follows: the radius at tooth tip of die is 1.6 mm; die semi-angle is 40°; splitting thickness is 2 mm and length of die bearing is 15 mm. After the practical verification with optimized process parameters, the machining allowance of gear end-face reduces to 1.91 mm and the collapse amount of gear tooth reduces to 0.29 mm. The practical results indicate that with the result parameters obtained from multi-objective optimization, qualified products can be produced.

Key words: response surface method; spur gear with large module; cold extrusion; numerical simulation

随着齿轮成形工艺研究的深入和市场需求的不断发展，现代制造业对齿轮产品精度要求不断提高，而齿轮的精密成形一直都是研究的热点^[1-2]。大模数直齿轮作为载重汽车轮边减速器中重要的零部件，精密塑性成形工艺主要为“冷挤压+冷整形”复合成形工艺，经冷挤压成形后的直齿轮齿面光洁，金属流线连续，轮齿承载能力高，因此逐渐成为直齿轮加工的主要方法。国内外学者对如何提高大模数直齿轮冷挤压成形质量、提高模具使用寿命，进行了大量研究并取得了显著成效。李倩^[3]采用数值模拟和实验相结合的方法，提出“热锻预成形—冷挤压—冷精整终成形”的大模数直齿轮成形新工艺，但未对成形质量进行说明。陈伟^[4]以模数为0.8的齿轮为研究对象，分析不同工艺参数对模具单位挤压力和成形精度的影响，但未考虑各因素对成形质量的影响。孟冠军等^[5-7]提出以曲面构造流线型齿形凹模型腔，数值模拟结果表明对改善充填和提高变形分布均匀性有显著的效果，但未经工艺实验证明。HU等^[8]提出将挤压凸模端面改为波形的方案，数值模拟和实验结果表明改进方案可以改善充填和降低成形载荷，但凸模端面波形加工较为复杂，实际应用有难度。夏玉峰等^[9]以入模角、毛坯直径系数、摩擦因数和压制速度为实验因素对成形载荷、齿形塌角和齿形精度进行多目标优化，但实验因素选择和实验结果有待商榷。FENG等^[10-11]采用FEM和田口法相结合的方法分别对斜齿轮热锻成形工艺参数和直齿轮热锻工艺参数进行优化，对直齿轮冷挤压成形工艺参数优化具有一定参考价值。这些研究大多数从直齿轮冷挤压成形性或单因素单目标分析成形过程方面入手，而较少采用多目标优化的方法对冷挤压齿轮成形质量和成形载荷进行平衡和优化。本文作者针对某厂生产的大模数直齿轮冷挤压工艺中出现的端面加工余量大、齿顶塌角大和成形载荷大的问题，提出采用数值模拟和实验设计相结合的方式，以响应面法作为优化方法，把端面加工余量、齿顶塌角量和成形载荷3个目标值进行平衡和优化，得出最佳工艺参数组合指导实际生产。

1  工艺方案分析

以模数m=4，齿数Z=16，压力角α=20°，变位系数x=0.45，材料为20CrMnTi的载重汽车用直齿轮作为研究对象，其冷挤压成形工艺为热锻制坯—球化退火—抛丸—车削制坯—磷化皂化—冷挤压，并采用“件压件”的形式连续通过齿形凹模。

冷挤压成形工艺示意图如图1所示。冷挤压齿轮缺陷如图2所示，齿轮下端齿顶部分出现填充不饱满的现象，下端不饱满长度L为5~7 mm，塌陷量δ为0.3~0.5 mm，下端端面外凸h为2.5~3.5 mm。虽然在设计挤压凹模时对齿顶进行了机加余量补偿，但挤压件成形质量不稳定，一些挤压件经车外圆后在齿轮下端齿顶处仍未见光，不能满足设计尺寸要求。导致冷挤压齿轮下端面外凸、下端齿顶充填不饱满的主要原因为：坯料与齿形模具接触面较大，金属流过齿形模时受到较大的摩擦阻力^[12]，并且在挤压成形时，下端均处于无背压或小背压状态，金属径向填充模具能力弱。

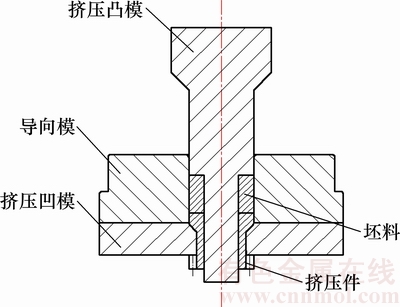
图1  冷挤压成形工艺示意图

Fig. 1  Diagram of cold extrusion process

图2  冷挤压齿轮件缺陷示意图

Fig. 2  Diagram of extruded gear defect

2  模型建立和实验设计

2.1  有限元模型建立

采用CATIA建立直齿轮冷挤压成形几何模型，对几何模型进行简化，并采用DEFORM-3D软件建立如图3所示的大模数直齿轮冷挤压有限元模型。

图3  3D有限元模型

Fig. 3  3D finite element model

为提高计算效率，取1/8模型进行模拟，模具定义为刚体，忽略模具的弹性变形，坯料定义为塑性体，坯料材料为AISI-4120，坯料1划分为100 000个网格，坯料2划分为30 000个网格。其余模拟参数见表1。

表1  部分模拟参数

Table 1  Parameters in simulation

2.2  工艺参数的选择及目标函数

对大模数直齿轮冷挤压成形质量和成形载荷影响较大的因素主要为齿形凹模的形状尺寸。因此，分别选取齿形凹模中的齿顶圆角R、入模角α、劈分角厚度T和定径带长度L作为本实验变量因素。根据经验，原齿形凹模工艺参数为：齿顶圆角R 1.2 mm，入模角α 45°，劈分角厚度T 2.5 mm，定径带长度L 5 mm。图4所示为齿形凹模的关键工艺参数。根据冷挤压后齿轮下端面外凸、下端齿顶充填不饱满和成形载荷大的问题，本文以挤压后齿轮的下端面外凸量h、下端齿顶塌角量δ和成形载荷F作为优化目标。

2.3  实验设计

响应面法的使用需确定合理的因素及相应的水平参数^[13]，本文主要针对齿顶圆角R、入模角α、劈分角厚度T和定径带长度L这4个工艺参数对齿轮的下端面外凸量h、下端齿顶塌角量δ和成形载荷F的影响进行研究。因此确定本实验的因素水平如表2所示。

应用四因素(x₁，x₂，x₃，x₄)五水平(-2，-1，0，1，2)的中心复合设计(CCD)进行实验设计，共计30次实验。部分实验方案及实验结果如表3所示。

图4  齿形凹模的关键工艺参数

Fig. 4  Critical process parameter of toothed die

表2  工艺参数及水平

Table 2  Process parameters and their levels

表3  实验方案及部分结果

Table 3  A portion of test program and results

2.4  响应面模型的建立

采用二阶模型建立3个目标响应δ，h和F关于设计变量的预测模型。应用最小二乘法对实验结果进行回归分析，得到关于3个目标响应函数为：

    (1)

         (2)

      (3)

应用方差分析对响应面模型进行显著性分析，结果如表4~6所示。

由表4~6可知：3个模型的显著性P值均为0.000 1，皆小于0.05(α=0.05)，说明得到的3个二阶回归模型是非常显著的。除F检验之外，可通过R²和来进一步检验所构建预测模型的可靠性，通常R²和越大，回归模型的拟合程度越好^[14]。决定系数如表7所示。从表7可以看出：所得到3个回归模型的R²值和较大，3个模型的拟合程度好，较大并且和差值小于0.2，说明3个模型具有较高的预测精度，3个模型的精密度均大于4，说明模型有足够的分辨力。综上所述，3个预测模型可较好地描述优化目标δ，h和F关于设计变量x₁，x₂，x₃和x₄的响应，并且具有满意的精度。

表4  下端齿顶塌角量δ方差分析

Table 4  Variance analysis of δ

表5  下端面外凸量h方差分析

Table 5  Variance analysis of h

表6  成形载荷F方差分析

Table 6  Variance analysis of F

选取影响各个响应目标最显著的交互因素进行分析。其中，对齿顶塌角量δ影响最为显著的交互因素为x₂(入模角)和x₃(劈分角厚度)；对端面外凸量h影响最为显著的交互因素是x₁(齿顶圆角)和x₂(入模角)；对成形载荷F影响最为显著的交互因素为x₂(入模角)和x₃(劈分角厚度)。

表7  决定系数

Table 7  Determination coefficient analysis

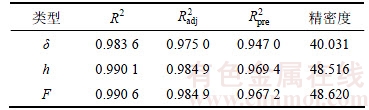
图5所示为x₁=1.4 mm，x₄=15 mm时响应目标函数δ关于变量x₂和x₃的三维曲面图和等值线图。从图5可以看出：对于变量x₂，齿顶塌角量δ的响应值随着变量x₂增加而变大。这是因为齿轮冷挤压成形为空心件带芯棒正挤压，除受齿形凹模工作表面摩擦影响以外，还受到芯棒表面摩擦的影响。因此剧烈变形区集中在齿形凹模入模口区，金属进入变形区前或离开变形区后，不发生塑性变形，只做刚性平移^[15]。而入模角增大，齿形凹模劈分坯料行程增加，外层金属流动缓慢，内外层金属流动不均匀，因此齿顶塌角量增大。对于变量x₃，齿顶塌角量δ的响应值随着变量x₃增加而变大。这是由于齿形凹模劈刃对坯料进行劈分，坯料向两侧齿形腔转移，劈分角厚度小，坯料容易被劈分而进入齿形腔，劈分角厚度越大，坯料不易被劈分而向上堆积，造成纵向毛刺和齿顶塌陷量增大。

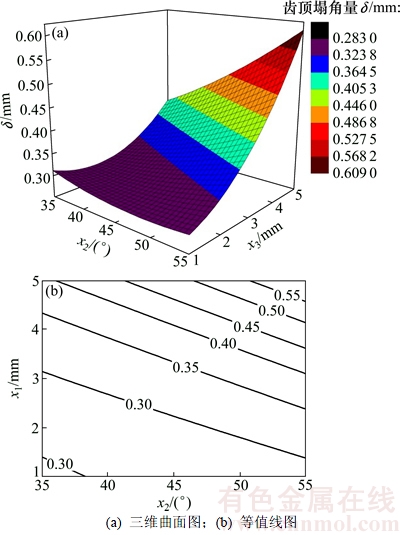
图5  x₁=1.4 mm，x₄=15 mm时δ关于变量x₂和x₃的三维曲面图和等值线图

Fig. 5  3D surface graph and contour for δ as x₂ and x₃ varies (x₁=1.4 mm, x₄=15 mm)

图6所示为x₃=3 mm，x₄=15 mm时响应目标函数h关于变量x₁和x₂的三维曲面图和等值线图。从图6可以看出：对于变量x₁，端面外凸量h的响应值随着变量x₁增加而减小。这是因为增大齿形凹模齿顶圆角可以改善金属流动^[16]，使内外层金属流动趋于均匀。对于变量x₂，端面外凸量h的响应值随着变量x₂增加而变大。这是因为入模角增大，坯料与齿形凹模接触面增加，摩擦阻力增大，表层金属流动减缓，齿轮端面外凸量增大。

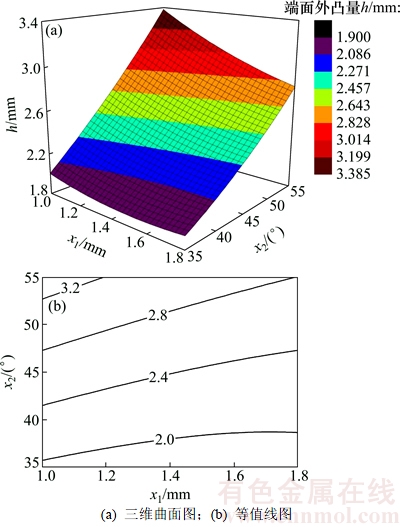
图6  x₃=3 mm，x₄=15 mm时h关于变量x₁和x₂的三维曲面图和等值线图

Fig. 6  3D surface graph and contour for objective response h as x₁ and x₂ varies (x₃=3 mm, x₄=15 mm)

图7所示为x₁=1.4 mm，x₄=15 mm时响应目标函数F关于变量x₂和x₃的三维曲面图和等值线图。从图7可以看出：对于变量x₂，成形载荷F的响应值随着变量x₂增加而减小；对于变量x₃，成形载荷F的响应值随着变量x₃增加而变大。

图7  x₁=1.4 mm，x₄=15 mm时F关于变量x₂和x₃的三维曲面图和等值线图

Fig. 7  3D surface graph and contour for F as x₂ and x₃ varies (x₁=1.4 mm, x₄=15 mm)

3  优化和验证

3.1  优化

采用上述响应面模型对x₁(齿顶圆角)、x₂(入模角)、x₃(劈分角厚度)和x₄(定径带长度)4个工艺参数进行优化，目标值δ(齿顶塌角量)、h(端面外凸量)和F(成形载荷)都得到最小值。设计变量的约束条件为：齿顶圆角R1.0~1.8 mm，入模角α 35~55 ℃，劈分角厚度T 1~5 mm，定径带长度L 10~25 mm。使用MATLAB软件求出可行设计空间中目标值最优解及对应的工艺参数组合：x₁(齿顶圆角)为1.6 mm、x₂(入模角)为40°、x₃(劈分角厚度)为2 mm和x₄(定径带长度)为15 mm。

3.2  验证

为验证优化结果得到工艺参数的准确性，为后续生产提供实际参考，以优化所得工艺参数进行数值模拟和工艺实验。工艺实验在4 MN液压机上进行，图8所示为冷挤压组合凹模，凹模采用三层组合式凹模，凹模模芯材料为YG15。冲头材料为Cr12MoV，坯料材质为20CrMnTi，挤压前对坯料进行球化退火和磷皂化润滑处理，工艺实验和数值模拟结果如图9所示。

图8  冷挤压组合凹模

Fig. 8  Combined die for cold extrusion

原模具挤压加工成形载荷约2 200 kN，采用优化后的模具进行加工，成形载荷约1 800 kN，降低约18.2%。采用三坐标测量仪对挤压后的齿轮进行测量，随机抽选5个齿轮进行检测，每次测量随机取3个齿，并与原模具生产的齿轮进行配对样本t检验，检验结果如表8和9所示。由表8可看出：采用原模具挤压成形的齿轮其平均齿顶塌角量为0.390 3 mm，平均端面外凸量为2.956 1 mm；采用优化模具挤压成形的齿轮其平均齿顶塌角量为0.285 1 mm，平均端面外凸量为1.906 5 mm。从图9可见：优化前与优化后齿顶塌角量和端面外凸量显著性值均小于0.05，故可认为优化后的模具可显著减小齿顶塌角量和端面外凸量。

根据测量数据拟合出优化前后齿轮齿顶轮廓，图10所示为优化前后成形齿轮塌角情况，采用优化后模具挤压成形的齿轮，其齿顶塌角量和端面外凸量相较于未优化模具成形的齿轮均得到改善，成形质量得到提高。

表8  成对样本统计量

Table 8  Paired samples statistics

图9  优化后挤压件和模拟件

Fig. 9  Extruded gear and simulation result

表9  成对样本检验

Table 9  Paired samples test

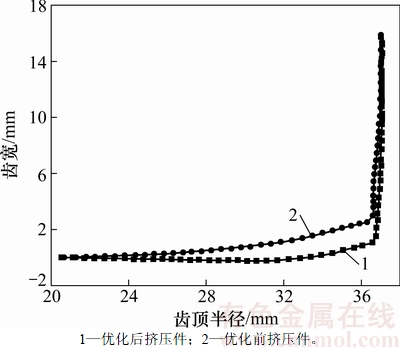
图10  优化前后成形齿轮塌角情况

Fig. 10  Reduction in addendum height of before and after optimization

响应面预测结果、数值模拟结果和实测结果对比如表10所示。由表10可看出：实测值较预测值和模拟值偏大，误差主要源于工艺实验中模具弹性变形引起的尺寸误差。响应面预测结果与实测值的相对误差绝对值小于5%，说明响应面法优化的工艺参数是合理的。

表10  响应面预测结果、数值模拟结果和实测结果的对比

Table 10  Comparison results of response surface

4  结论

1) 基于响应面法(RSM)，分别建立3个目标响应齿顶塌角量δ，端面外凸量h和成形载荷F，关于设计变量齿顶圆角、入模角、劈分角厚度、定径带长度的二阶响应模型，得到的回归模型拟合度分别为98.36%，99.01%和99.06%，预测精度较好，能较好地描述3个目标函数关于设计变量的响应。

2) 运用MATLAB软件对实验参数进一步进行优化，得到大模数直齿轮冷挤压成形最优工艺参数：齿顶圆角为1.6 mm、入模角为40 ℃、劈分角厚度为2 mm、定径带长度为15 mm。

3) 采用优化工艺参数组合，能有效降低齿顶塌角量、端面外凸量和成形载荷，为类似大模数直齿轮的冷挤压生产提供了一定生产实践的指导作用。

参考文献：

[1] 冯再新, 周贤宾, 张治民, 等. 齿轮精密成形精整毛坯设计[J]. 塑性工程学报, 2006, 13(1): 67-70.

FENG Zaixin, ZHOU Xianbin, ZHANG Zhimin, et al. Designing of semifinished product for spur gear precision forming[J]. Journal of Plasticity Engineering, 2006, 13(1): 67-70.

[2] 周瑞, 陈文琳, 李亨, 等. 基于弹性变形行为的冷精整直齿轮尺寸预测[J]. 塑性工程学报, 2013, 20(5): 27-32.

ZHOU Rui, CHEN Wenlin, LI Heng, et al. Dimension prediction of spur gear in cold precision sizing based on elastic deformation behavior[J]. Journal of Plasticity Engineering, 2013, 20(5): 27-32.

[3] 李倩. 大模数高厚度直齿轮精密成形工艺数值模拟及试验研究[D]. 北京: 机械科学研究总院, 2011: 65-67.

LI Qian. Numerical simulation and experimental research on precise forging process for large module and high thickness spur gear[D]. Beijing: China Academy of Machinery Science & Technology, 2011: 65-67.

[4] 陈伟. 圆柱直齿轮正挤压成形参数分析及工艺优化[D]. 上海: 上海工程技术大学材料工程学院, 2010: 77-78.

CHEN Wei. Direct extrusion forming parametric analysis of spur gear and process optimization[D]. Shanghai: Shanghai University of Engineering Science. School of Materials Science and Engineering, 2010: 77-78.

[5] 孟冠军. 直齿轮冷挤压成型若干关键技术研究[D]. 合肥: 合肥工业大学材料科学与工程学院, 2005: 58-59.

MENG Guanjun. Research on the key technology of cold forging of spur gear[D]. Hefei: Hefei University of Technology. School of Materials Science and Engineering, 2005: 58-59.

[6] 王银冰. 直齿圆柱齿轮冷静段数值模拟机挤压腔造型参数优化[D]. 合肥: 合肥工业大学材料科学与工程学院, 2006: 50-51.

WANG Yinbing. Numerical simulation and parameter optimization of female die molding in precision forging of spur gear[D]. Hefei: Hefei University of Technology. School of Materials Science and Engineering, 2006: 50-51.

[7] 刘全坤, 李冬生. 基于流线型凹模型腔的直齿圆柱齿轮冷挤压数值模拟分析[J]. 工程设计学报, 2005, 12(1): 15-19.

LIU Quankun, LI Dongsheng. Numerical simulation analysis of cold extrusion for spur gear based on streamline cavity[J]. Journal of Engineering Design, 2005, 12(1): 15-19.

[8] HU Chengliang, WANG Kesheng, LIU Quankun. Study on a new technological scheme for cold forging of spur gears[J]. Journal of Materials Processing Technology, 2007, 187: 600-603.

[9] 夏玉峰, 叶彩虹, 王力, 等. 基于响应面发的直齿轮冷挤压工艺多目标优化[J]. 华中科技大学学报(自然科学版), 2016, 44(1): 70-75.

XIA Yufeng, YE Caihong, WANG Li, et al. Multi-objective optimization of cold extrusion process for planetary spur gear based on RSM[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2016, 44(1): 70-75.

[10] FENG Wei, HUA Lin. Multi-objective optimization of process parameters for the helical gear precision forging by using Taguchi method[J]. Journal of Mechanical Science and Technology, 2011, 25(6): 1519-1527.

[11] CHEN Xuewen, JUNG Dongwon, SUN Aixue. Gear hot forging process robust design based on finite element method[J]. Journal of Mechanical Science and Technology, 2008, 22(9): 1772-1778.

[12] SONG J H, IM Y T. The applicability of process design system for forward extrusion of spur gears[J]. Journal of Materials Processing Technology, 2007, 184: 411-419.

[13] PALANIVEL R, MATHEWS P K. Prediction and optimization of process parameter of friction stir welded AA5083-H111 aluminum alloy using response surface methodology[J]. Journal of Central South University, 2012, 19(1): 1-8.

[14] ZHOU Jie, ZHUO Fang, Huang Lei, et al. Multi-objective optimization of stamping forming process of head using Pareto-based genetic algorithm[J]. Journal of Central South University, 2015, 22(9): 3287-3295.

[15] 洪慎章. 冷挤压实用技术[M]. 北京: 机械工业出版社, 2005: 19-20.

HONG Shenzhang. Cold extrusion technology[M]. Beijing: China Machine Press, 2005: 19-20.

[16] 陈伟, 陈晖, 李名尧. 齿根圆角半径对齿轮冷锻成形的影响[J]. 热加工工艺, 2011, 40(1): 97-99.

CHEN Wei, CHEN Hui, LI Mingyao. Effect of addendum fillet radius on cold forging for gears[J]. Hot Working Technology, 2011, 40(1): 97-99.

(编辑  赵俊)

收稿日期：2016-12-08；修回日期：2017-03-18

基金项目(Foundation item)：国家自然科学基金资助项目(51275543)；重庆市科委应用开发项目(cstc2014yykfC70003)(Project(51275543) supported by the National Natural Science Foundation of China; Project(cstc2014yykfC70003) supported by the Science & Technology Application Development Program of Chongqing)

通信作者：周杰，博士，教授，从事模具技术及模具CAD/CAM/CAE研究；E-mail：woliangniliu@163.com