Trans. Nonferrous Met. Soc. China 29(2019) 764-774

A modified constitutive model and hot compression instability behavior of Cu-Ag alloy

Meng-han WANG, Yong-chao YANG, Shun-li TU, Kang WEI

College of Material Science and Engineering, Chongqing University, Chongqing 400030, China

Received 8 March 2018; accepted 11 October 2018

Abstract: The hot compressive deformation behaviors of Cu-6wt.%Ag alloy were studied experimentally in the temperature range of 973-1123 K and the strain rate range of 0.01-10 s^-1. The stress increases and reaches the maximum value when the true strain is very small, and then the stress changes slowly and tends to be stable under the action of work hardening, dynamic recovery and recrystallization. The material parameters of the conventional Arrhenius constitutive model are only related to strain under different deformation conditions, and the prediction error is large, which cannot accurately characterize the hot deformation behavior of the alloy. To describe the hot deformation behavior of the alloy accurately, a modified constitutive model was established by considering the simultaneous influence of forming temperature, strain rate and strain. The results indicate that correlation coefficient (R) and the average absolute relative error (AARE) are 0.993 and 4.2%, respectively. The modified constitutive model can accurately describe the hot deformation behavior of Cu-6wt.%Ag alloy.

Key words: Cu-Ag alloy; intragranular recrystallization; crack; modified Arrhenius model

1 Introduction

High-strength, high conductivity material is used extensively in the construction of high-field magnets. Cu-Ag alloys have attracted much attention, due to their excellent mechanical properties and electrical conductivity [1-3]. The α-matrix of Cu and the Ag-rich strengthened phase in the Cu-Ag alloy can usually be deformed by cold drawing, so that the Ag fibrosis on the Cu matrix can be transformed into a biphasic fiber composite structure. The tensile strength and elastic modulus of Cu-Ag alloy tend to saturate with the increase of deformation degree [4]. RAJU et al [5] had shown that a combination of high strength and excellent ductility could be achieved in supersaturated Cu-3at.%Ag alloy by annealing after rolling at liquid nitrogen temperature (LNT). The evolution of the microstructure in cryorolled Cu-3at.%Ag alloy during isothermal annealing at 350 °C for 120 min was studied in detail. The reasons leading to the formation of an inhomogeneous microstructure were described experimentally and theoretically. ZHANG et al [6] studied the microstructures and properties of Cu/Ag (Invar) composites fabricated by powder metallurgy. It was shown that the heterogeneity of the dislocation structure was mainly caused by the development of an inhomogeneous solute Ag in the initial stage of annealing [7]. With the precipitation of solute Ag atoms in Cu matrix, the dissolution of Ag in Cu matrix decreases gradually, and the strength and hardness of the alloy increase by 22%. The fine continuous precipitate was formed near 475 °C, resulting in the best combination of high hardness, high strength, high ductility and low resistivity [8]. Processing map of Cu-Ag alloy was studied, which revealed the determinate regions where individual metallurgical process occurs and the limiting conditions of flow instability regions [9,10]. It is found that the strength of Cu-Ag alloy in high-pressure torsion is significantly higher than that of pure Cu. When the composite phase of the layered Cu-Ag decreases below 5 nm, the fibrosis appears, and the yield strength and microhardness of Cu-Ag alloy interact with each other [11,12].

At present, there have been a lot of researches about theoretical model establishment of Cu-Ag alloy strengthening and conductivity [4,5,7,13-18]. Although these studies explain variation between strength and conductivity of Cu-Ag alloy in different deformation stages of microstructure, the analysis of stress-strain curve is very rare. Also, although the Cu-Ag alloy has good ductility at low temperature, it is easy to crack under the condition of hot deformation. The microstructure evolution of Cu-Ag alloy is an essential cause of cracking. The evolution can be controlled effectively by thermal processing. Therefore, the research for the hot deformation behavior of Cu-Ag alloy has essential significance. The constitutive equation is an important tool to characterize the flow properties of materials, which can not only characterize the plastic flow characterization of materials directly, but also use infinite element analysis software for the numerical simulation of the forming process.

In this work, the flow behavior and the deformation mechanism of Cu-6wt.%Ag alloy were studied by microstructure evolution analysis in the high temperature plastic deformation process. Moreover, an improved constitutive model was introduced, which can describe the flow properties of the alloy relatively accurately and provide a theoretical basis for the formulation of the hot working process of Cu-6wt.%Ag alloy.

2 Experimental

2.1 Material preparation and hot compression procedure

The experimental samples of Cu-6wt.%Ag alloy were obtained by sectioning a cast bar into several samples (with a diameter of 8 mm and a height of 12 mm). The experiment was carried out on the test machine Thermecmaster-Z. The samples were heated to the set temperature of 750 °C at a heating rate of 10 °C/s. In order to reduce the influence of the temperature gradient inside the sample on hot compression deformation, when the sample was heated to the set temperature, an insulation process of 180 s was adopted to make the sample temperature uniform. And the lubricant and the graphite sheets were coated at two ends of the samples to reduce the influence of the friction on the stress state, and avoid uneven deformation. The schematic diagram of the hot compression test process is shown in Fig. 1.

The thermal compression temperatures were 973, 1023, 1073 and 1123 K, respectively, and the strain rates were 0.01, 0.1, 1 and 10 s^-1, respectively. The amount of reductant in each experiment was 50%. Finally, the nitrogen quenching was utilized to retain the microstructure of the simples after the hot deformation. The samples were cut along the longitudinal direction, and the microstructure was observed under the microscope after grinding, polishing, and 30-50 s corrosion of FeCl₃ (10 g) + H₂O (100 mL) + HCl (30 mL) mixed corrosion liquid. The stress-strain relationships under different conditions are shown in Fig. 2.

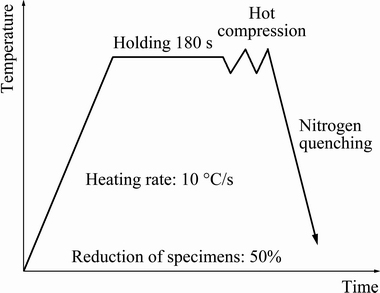
Fig. 1 Experiment procedure for hot compression tests

2.2 Deformation behavior of hot compression

As shown in Fig. 2, the temperature and strain rate have great effect on high temperature deformation behavior of Cu-6wt.%Ag alloy. In the compression experiments of Cu-6wt.%Ag alloy under high temperatures, the flow stress increases significantly when the strain increases to a certain extent because work hardening and deformation resistance of alloy increase rapidly in the initial stage of deformation. With the further deformation of the specimen, the flow stress trends to be stable by dynamic recovery and recrystallization. At low temperature stage, because of low thermal activation energy, less accumulated energy and weak dynamic softening, work hardening plays a major role. There is no enough time to coordinate deformation by means of dislocation and grain movements. The multiplication of dislocation leads to the improvement of stress level at high strain rate [19]. Finally, under the action of work hardening and dynamic softening [20-22], flow stress tends to be stable.

In order to understand the high temperature deformation characteristics of the alloy, the micro- structure of the alloy was observed. As shown in Fig. 3, at the deformation temperature of 1123 K and different strain rates (0.01 and 10 s^-1). It can be seen from Fig. 3 that the grain is gradually thinning with the increase of strain rate, when the deformation temperature is 1123 K. The reason may be that the deformation temperature is high enough at low strain rate, and the atoms on the grain boundary tend to deviate from their equilibrium position, leading to a larger energy of the grain boundary. The high energy regions generate at the grain boundary, and then recrystallize and grow up after reaching the energy threshold, as shown in Fig. 3(a). With the increase of strain rate, dynamic recrystallization occurs in a large range. When the strain rate reaches 10 s^-1, the energy caused by plastic deformation increases and a large range of dynamic recrystallization occurs. Recrystallized grains are refined due to growth hindrance, as shown in Fig. 3(b).

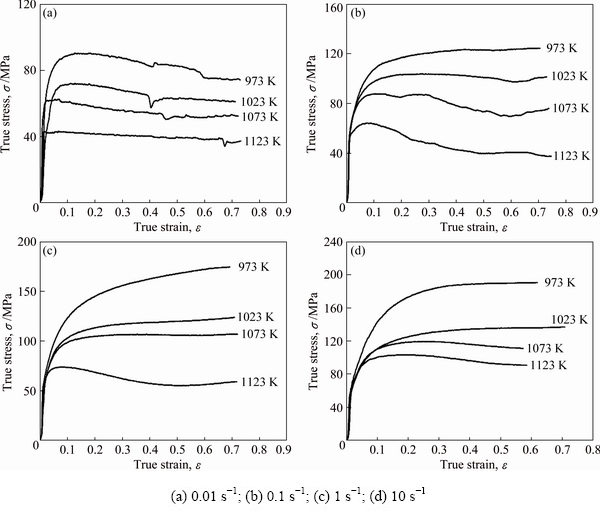
Fig. 2 True stress-strain curves for Cu-Ag alloy under different deformation conditions

Fig. 3 Microstructures of Cu-Ag alloy at 1123 K with different strain rates

It is worth noting that under some conditions (0.1 s^-1, 1023 K; 0.1 s^-1, 1073 K; 1 s^-1, 1123 K), the stress increases rapidly, when the strain reaches 0.55. Based on the discussion on the flow properties, microstructure evolution and theoretical instability region of Cu-Ag alloy at high strain rate [9], it is found that the plastic deformation mechanism of the material changes with the intense evolution of microstructure at high strain rate and high temperature (1023-1123 K). With the increase of strain rate, the appearance of twinning and micro-cracks and other structural defects leads to a large amount of stacking of dislocations near grain boundaries, and further causes stress concentration. The stress concentration at grain boundaries cannot efficiently be released, which is conducive to the formation of the twinning. The twin boundary appears in the Cu-Ag alloy with the multi-slip system, which hinders the dislocation slip during further deformation. The effect of work hardening is more remarkable than that of dynamic recrystallization, and the flow stress changes and increases suddenly, when the strain is about 0.55.

At the same time, as the stress concentration at grain boundary intensifies, the stored energy of grain boundary increases rapidly, and the energy consumed by forming twinning is not high enough to counteract it. Therefore, the material gradually shows the microscopic characteristics that may lead to instability, the microstructure of the material shows instability and forms the micro-cracks [23], as shown in Fig. 4(a). Not only can the dynamic recrystallization and grain twinning hinder dislocation slip, but also the nucleation of dynamically recrystallized grains in the initial microstructure is also one of the critical factors that cause the sudden change of flow stress. Figure 4 shows the microstructure of the alloy at strain temperature of 850 °C and strain rate of 1 s^-1 with the reduction of nearly 40% (strain 0.55). Obviously, the dynamic recrystallization nucleates and grows not only at the primary grain boundaries but also in some grains with the increase of the strain, as shown in Fig. 4(b).

Fig. 4 Microstructures of Cu-Ag alloy at 1123 K with strain  of 0.55 and strain rate of 1 s^-1

3 Constitutive equation for Cu-Ag alloy

The precise constitutive models of the material are the prerequisite of the finite element numerical simulation technique, which is the key of obtaining the dynamic response and thermal physics parameters of the forging forming process. For the Cu-Ag alloy, the change of the macroscopic mechanical properties of the material during the high temperature plastic forming process is the result of the work hardening, dynamic recovery, and dynamic recrystallization. The variation of the parameters of the material during the thermal deformation process does not belong to a simple linear law with the change of temperature and stain rate.

3.1 Original Arrhenius constitutive model

Phenomenological plastic constitutive models are widely used in the simulation of the forming processes of metals or alloys at high strain rate and high temperature. The Arrhenius equation is one of the most frequently used phenomenological models [24], which can describe the relationship among the flow stress, strain rate and deformation temperature.

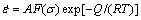                      (1)

                  (2)

where 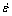 is the strain rate (s^-1); σ is the flow stress (MPa); Q is the activation energy of hot deformation (kJ/mol); R is the mole gas constant (8.314 J/(mol·K)); T is the thermodynamic temperature (K); n and n ₁ are the materials stress indexes; A, α and β are the material constants which are experimentally determined (α=β/n₁).

According to Zener-Hollomon research [24], the strain rate factor Z compensated by temperature can synthesize the effect of deformation temperature T and strain rate 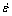 on the flow stress.

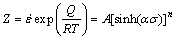                 (3)

3.1.1 Determination of material constants

The material constants of the constitutive equation can be determined using the stress-strain data obtained from hot compression tests. For the low stress level (ασ<0.8) and high stress level (ασ>1.2), bringing the power law and exponential law of F(σ) into Eq. (1) and taking natural logarithm on both sides of Eq. (1), it can be transformed to the following forms, respectively.

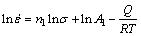                      (4)

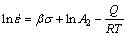                        (5)

where A₁ and A₂ are the material constants, which are independent of the deformed temperatures.

Figures 5(a) and (b) shows the relationships of 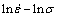 and 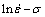 under different deformation temperatures, respectively. The linear relationship with a similar slope is observed under different temperatures. The slope of every line can be obtained by linear fitting method. The mean value of the slopes under temperatures of 973, 1023, 1073 and 1123 K is accepted as material constant n₁, and the mean value of the slopes under different strain rate is accepted as material  constant β, thus the values of n₁ and β are obtained as 5.89897 and 0.06856 MPa^-1, respectively, and α=β/n₁= 0.01162 MPa^-1.

3.1.2 Determination of activation energy Q

For all the stress levels, by rearranging Eq. (1) and taking the natural logarithm of Eq. (1) respectively, we obtain

                (6)

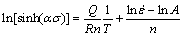                (7)

The activation energy Q of hot deformation can be described as the following equation.

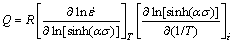        (8)

When the temperature is a constant, there is a linear relationship between 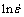 and ln[sinh(ασ)], as drawn in Fig. 5(c), and the mean value of the slopes under the different temperatures is accepted as n. Similarly, if  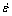is a constant, the relationship between ln[sinh(ασ)] and 1/T could be obtained, as drawn in Fig. 5(d), the mean value of the slopes is accepted as Q/(Rn). So, the values of n and Q could be respectively calculated from the slopes of the fitting lines shown in Fig. 5, where n=5.899 and Q=420.458 kJ/mol. Bringing all the material constants into Eq. (6), we can obtain ln A=41.878.

The studies had shown that the strain has obvious effects on the material constants [21]. Because the constitutive model is based on the steady flow of materials in plastic deformation, the solution of the constitutive equation does not take into account the effect of strain on the flow stress. The effects of strain accumulation on flow stress cannot be ignored when establishing the proper constitutive equations. In order to study the change of material parameters in the constitutive equation under different deformation degrees, the material constants (α, n, Q and ln A) can be viewed as polynomials about stain with a range of 0.1-0.65 at an interval of 0.05; the curves are shown in Fig. 6. As shown in Eq. (9), these constants can be expressed as polynomials of 6-order with strain. The results of polynomial fitting are listed in Table 1.

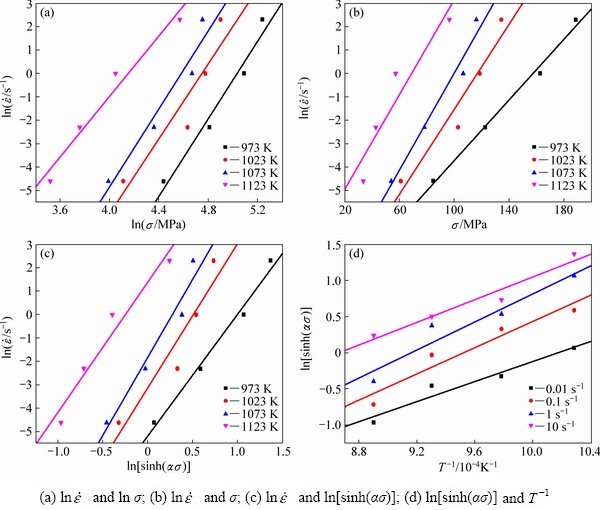
Fig. 5 Relationships among hot deformation parameters

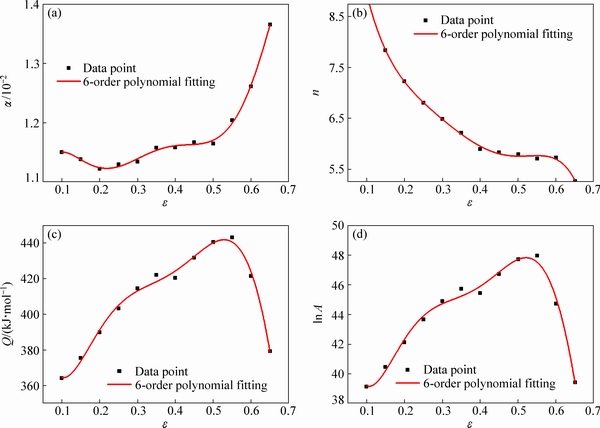
Fig. 6 Variations of α (a), n (b), Q (c) and ln A (d) with true strain by 6-order polynomial fitting

Table 1 Coefficients of polynomial for material parameters

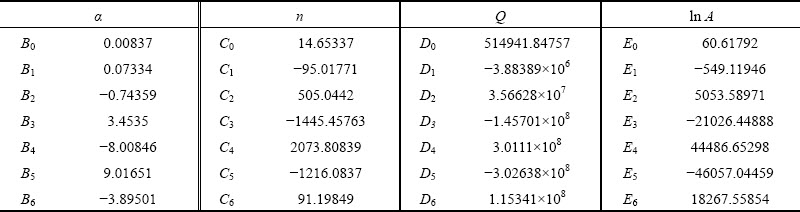
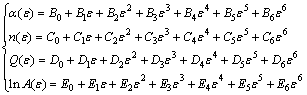  (9)

3.1.3 Construction of constitutive equation

The material constants have been evaluated, and the flow stress can be described by the constitutive equation which links flow stress and Z-H parameter at different strains with a form in Eq. (10):

   (10)

3.2 Error source analysis of original constitutive model

The accuracy of the established model can be verified by comparing the experimental data with the data predicted by the model, as shown in Fig. 7. We can see that the trend of the predicted curve is consistent with the experimental values. Under most of deformation conditions, the model can predict the flow stress accurately, but under some deformation conditions, the difference between the predicted value and the experimental value is quite large. The deviation between the model prediction value and the experimental value is obvious and bidirectional. The predicted value is larger and smaller under different deformation conditions. In some cases, the predicted values are in good agreement with the experimental values, which shows that the model cannot improve the prediction accuracy by using simple linear correction.

Fig. 7 Comparison between experimental and predicted flow stress curves under different deformation conditions

Based on previous research results and analysis, the deviation between the predicted value and the experimental value might be caused by the clear solution of the model. In the model, the material parameters such as n, n ₁, A, α, β and Q are assumed to be constants related to deformation temperature or strain rate, but the parameters are taken the mean, in other conditions. However, for some material parameters, the calculated values under different deformation conditions have great gaps with the mean, such as the solution of β. As shown in Fig. 5(b), the slopes of the line represent the values of β under different temperatures. As the temperature increases, the slope of the line gradually decreases. When the temperature is 1073 K, the slope of the line has a significant deviation compared with the slopes under other conditions. This indicates that β is not a constant at different temperatures, and β should be expressed as variables related to deformation temperature and strain. SHI and CHEN [25] also showed similar views about the related variables.

By Eq. (8), the activation energy Q of thermal deformation is a constant independent of the thermal deformation condition in the established model. However, through the calculation of Q value under different deformation conditions, it is found that the deformation condition has a significant effect on the thermal activation energy. In addition, SHASTRY et al [26] found that the thermal deformation condition had a significant effect on the thermal activation energy in 2.5Cr-1Mo steel.

3.3 Modification of constitutive model

To improve the prediction accuracy of the constitutive model under hot deformation, the influence of thermodynamic parameters on material parameters should be considered in the model to correct it using a modified constitutive model as follows:

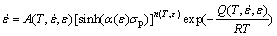 (11)

Taking natural logarithm on both sides of Eq. (11), we obtain

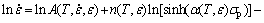
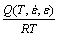                   (12)

Equation (12) can be transformed into the following forms [27]:

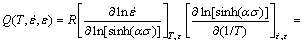
            (13)

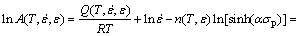
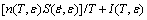   (14)

Based on the universal global optimization algorithm, the binary polynomial fitting of the material parameters can be used to reflect the relationship among n, I, S and T, ε, 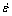, as shown in Fig. 8. At the same time, the fitting polynomials of material parameters can be expressed as follows:

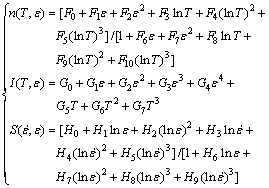   (15)

The results of polynomial fitting are listed in Table 2, and the material parameters under certain deformation conditions can be derived according to Eq. (15).

Table 2 Coefficients of polynomials for material parameters

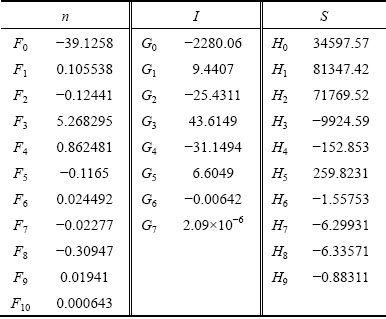
The predicted flow stress values of the modified model are compared with the experimental values and the results are shown in Fig. 9. It can be seen that the predicted flow stress values of the modified model are highly consistent with the experimental values under most deformation conditions. The modified models all show high prediction accuracy.

3.4 Evaluation of accuracy of constitutive models

Based on the above analysis, both the original Arrhenius model and the Arrhenius model with deformation condition compensation were established.

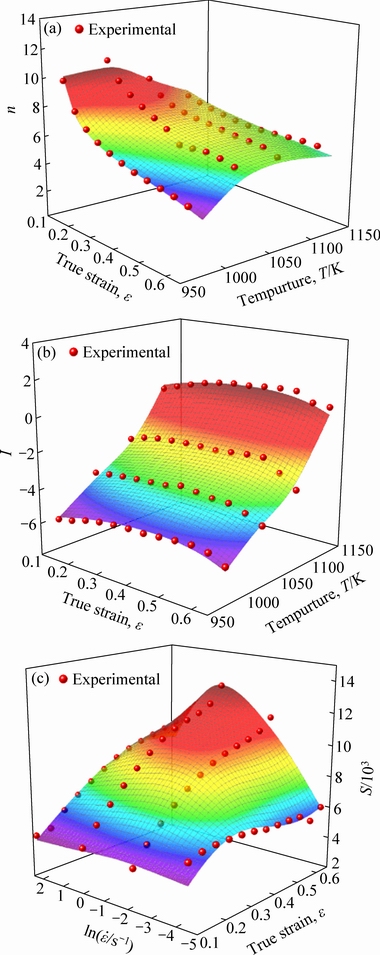
Fig. 8 Variation of n (a), I (b) and S (c) by polynomial fitting

Then, the accuracy of the two models was evaluated, as plotted in Fig. 10. Moreover, in order to quantitatively evaluate the prediction accuracy of the model, average absolute relative error (AARE) and correlation coefficient (R) are introduced and expressed as follows:

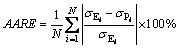               (16)

             (17)

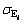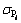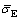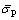where and are the experimental and predicted flow stress values, respectively;  and  are the mean values of the experimental and predicted flow stress, respectively; N is the total number of statistical samples [19,28]. The correlation coefficient R can reflect the closeness of the linear relationship between the experimental values and the predicted values; average absolute relative error AARE is an unbiased estimator, which can accurately reflect the degree of deviation between experimental values and the predicted values. After calculation, the correlation coefficient between the predicted values and the experimental values of the modify model is 0.993, and the average absolute relative error is 4.2%. Compared with their previous values of 0.97 and 9%, the correlation coefficient and average absolute relative error have been significantly improved, as shown in Fig. 10. It is proved that the modify constitutive model can effectively characterize the high temperature flow properties of Cu-6wt.%Ag alloy.

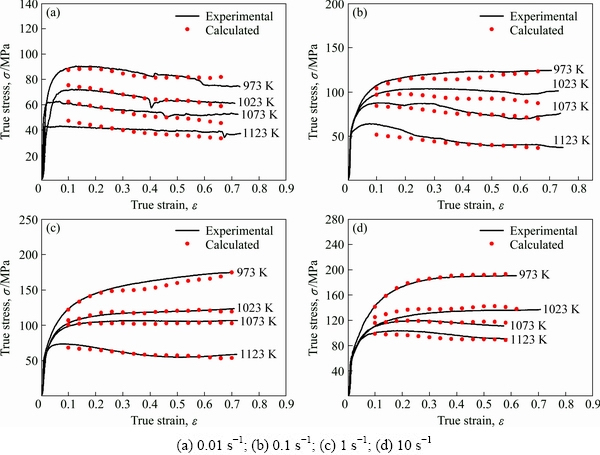
Fig. 9 Comparison between experimental and calculated flow stress of modified model under different deformation conditions

Fig. 10 Comparison between experimental flow stress and original calculated flow stress (a) and calculated flow stress with modified model (b)

4 Conclusions

(1) The flow behavior of Cu-6wt.%Ag alloy has been analyzed through compression tests in temperature range of 973-1123 K and strain rate range of 0.01-10 s^-1. The deformation characteristics indicate the flow stress increases when strain rate increases and temperature decreases. Work hardening and dynamic recrystallization can be observed from the flow curves.

(2) The microstructure evolution and flow properties of Cu-6wt.%Ag alloy were studied based on material deformation theory. It is found that the twinning of phase transformation and dynamic recrystallization occur in Cu-6wt.%Ag alloy during deformation at high strain rate. The microstructure transformation leads to the increase of dissipative energy of the material, and micro-cracks and instability occur at high strain rate.

(3) The Arrhenius constitutive model was established to predict the flow stress, material parameters under the coupling of strain, temperature and strain rate are obtained by multi-dimensional fitting. The modify constitutive model was verified, the correlation coefficient changed from 0.97 to 0.993, and average absolute relative error changed from 9% to 4.2%. A modified constitutive model with the better predictive ability is obtained.

References

[1] EI-KHALEK A M A. Effect of pre-deformation and phase transformation on the creep behaviour of Ag-1wt%Cu alloy [J]. Materials Science and Engineering A, 2010, 527: 4818-4822.

[2] NING Yuan-tao, ZHANG Xiao-hui, WU Yue-jun. Electrical conductivity of Cu-Ag in situ filamentary composites [J]. Transactions of Nonferrous Metals Society of China, 2007, 17(2): 378-383.

[3] CHIBA A. Quantitative analysis of work hardening and dynamic softening behaviors of Cu-6wt pct Ag binary alloy based on true stress vs strain curves [J]. Acta Metallurgica Sinica (English Letters), 2012, 24(6): 420-434.

[4] SAKAI Y, INOUE K, ASANO T. Development of high-strength, high-conductivity Cu-Ag alloys for high-field pulsed magnet use [J]. Applied Physics Letters, 1991, 59(23): 2965-2967.

[5] RAJU K S, SARMA V S, KAUFFMANN A. High strength and ductile ultrafine-grained Cu-Ag alloy through bimodal grain size, dislocation density and solute distribution [J]. Acta Materialia, 2013, 61(1): 228-238.

[6] ZHANG Xin, WU Dan, YANG Lei, SHI Chang-dong, WU Yu-cheng, TANG Wen-ming. Microstructures and properties of Cu/Ag(Invar) composites fabricated by powder metallurgy [J]. Transactions of Nonferrous Metals Society of China, 2017, 27(8): 1759-1766.

[7] GUBICZA J, HEGEDUS Z, LABAR J L, KAUFFMANN A, FREUDENBERGER J, SUBRAMANYA S V. Solute redistribution during annealing of a cold rolled Cu-Ag alloy [J]. Journal of Alloys and Compounds, 2015, 623: 96-103.

[8] ZHAO Cong-cong, ZUO Xiao-wei, WANG En-gang, NIU Rong-mei, HAN Ke. Simultaneously increasing strength and electrical conductivity in nanostructured Cu-Ag composite [J]. Materials Science and Engineering A, 2016, 652: 296-304.

[9] WANG Meng-han, HUANG Long, CHEN Ming-liang. Processing map and hot working mechanisms of Cu-Ag alloy in hot compression process [J]. Journal of Central South University, 2015, 22(3): 821-828.

[10] WU Yu-cai. The study on industrialization of high-speed railway copper alloy contact wire and copper flat wire [D]. Beijing: General Research Institute for Nonferrous Metals, 2012: 17-33. (in Chinese)

[11] TIAN Y Z, LI J J, ZHANG P, WU S D, ZHANG Z F, KAWASAKI M, LANGDON T G. Microstructures, strengthening mechanisms and fracture behavior of Cu-Ag alloys processed by high-pressure torsion [J]. Acta Materialia, 2012, 60(1): 269-281.

[12] TIAN Y Z, WU S D, ZHANG Z F, FIGUEIREDO R B, GAO N, LANGDON T G. Strain hardening behavior of a two-phase Cu-Ag alloy processed by high-pressure torsion [J]. Scripta Materialia, 2011, 65(6): 477-480.

[13] HAMANA D, BOUMAZA L. Precipitation mechanism in Ag-8wt.% Cu alloy [J]. Journal of Alloys and Compounds, 2009, 477(1-2): 217-223.

[14] LIU J B, MENG L, ZENG Y W. Microstructure evolution and properties of Cu-Ag microcomposites with different Ag content [J]. Materials Science and Engineering A, 2006, 435-436: 237-244.

[15] ZUO Xiao-wei, HAN Ke, ZHAO Cong-cong, NIU Rong-mei, WANG En-gang. Microstructure and properties of nanostructured Cu-28wt.%Ag microcomposite deformed after solidifying under a high magnetic field [J]. Materials Science and Engineering A, 2014, 619: 319-327.

[16] JIA N, ROTERS F, EISENLOHR P, RAABE D, ZHAO X. Simulation of shear banding in heterophase co-deformation: Example of plane strain compressed Cu-Ag and Cu-Nb metal matrix composites [J]. Acta Materialia, 2013, 61(12): 4591-4606.

[17] LIU J B, ZHANG L, YAO D W, MENG L, Microstructure evolution of Cu/Ag interface in the Cu-6wt.%Ag filamentary nanocomposite [J]. Acta Materialia, 2011, 59(3): 1191-1197.

[18] LU Yue, MA Ru, WANG Yi-nong. Texture evolution and recrystallization behaviors of Cu-Ag alloys subjected to cryogenic rolling [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(9): 2948-2957.

[19] LIN Yong-cheng, LI Kuo-kuo, LI Hong-bin, CHEN Jian, CHEN Xiao-min, WEN Dong-xu. New constitutive model for high-temperature deformation behavior of inconel 718 superalloy [J]. Materials & Design, 2015, 74: 108-118.

[20] HAN Ying, WU Hua, ZHANG Wei, ZOU De-ning, LIU Gui-wu, QIAO Guan-jun. Constitutive equation and dynamic rescrystallization behavior of as-cast 254SMO super-austenitic stainless steel [J]. Materials & Design, 2015, 69: 230-240.

[21] LIN Yong-cheng, WEN Dong-xu, DENG Jiao, LIU Guan, CHEN Jian. Constitutive models for high-temperature flow behaviors of a Ni-based superalloy [J]. Materials & Design, 2014, 59: 115-123.

[22] LI Hang-zhou, XIONG Guang-dong, ZHAO Gui-ping. An elasto-plastic constitutive model for soft rock considering mobilization of strength [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(3): 822-834.

[23] RAO A C U, VASU V, GOVINDARAJU M. Stress corrosion cracking behaviour of 7xxx aluminum alloys: A literature review [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(6): 1447-1471.

[24] MCQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Materials Science and Engineering A, 2002, 322: 43-63.

[25] SHI C, CHEN X G. Effect of Zr addition on hot deformation behavior and microstructural evolution of AA7150 aluminum alloy [J]. Materials Science and Engineering A, 2014, 596: 183-193.

[26] SHASTRY C G, PARAMESWARAN P, MATHEW M D. The effect of strain rate and temperature on the elevated temperature tensile flow behavior of service-exposed 2.25Cr-1Mo steel [J]. Materials Science and Engineering A, 2007, 465: 109-115.

[27] SHI C J, MAO W M, CHEN X G. Evolution of activation energy during hot deformation of AA7150 aluminum alloy [J]. Materials Science and Engineering A, 2013, 571: 83-91.

[28] QUAN Guo-zheng, LIANG Jian-ting, LV Wen-quan, WU Dong-sen, LIU Ying-ying, LUO Gui-chang, ZHOU Jie. A characterization for the constitutive relationships of 42CrMo high strength steel by Artificial neural network and its application in isothermal deformation [J]. Materials Research, 2014, 17(5): 1102-1114.

Cu-Ag合金高温压缩本构模型的修正和失稳行为

王梦寒，杨永超, 涂顺利，危 康

重庆大学 材料科学与工程学院，重庆 400030

摘  要：基于热物理实验研究Cu-6wt.%Ag合金在温度为973~1123 K、应变速率为0.01~10 s^-1条件下的热变形行为。研究发现，当真应变较小时，应力随应变的增加迅速增加直至达到最大值，随后在加工硬化、动态回复和再结晶的共同作用下应力变化缓慢并趋于稳定；常规Arrhenius本构模型中材料参数在不同变形条件下仅与应变相关，预测误差较大，无法准确表征材料的热流变行为。为了准确描述合金的热变形行为，本文作者建立考虑变形温度、应变速率和应变三者协同影响的修正本构模型。结果表明，修正模型的相关系数和平均相对误差分别为0.993和4.2%，能较准确地描述Cu-6wt.%Ag合金的热变形行为。

关键词：铜银合金；晶内再结晶；裂纹；Arrhenius模型修正

(Edited by Wei-ping CHEN)

Foundation item: Project (51675061) supported by the National Natural Science Foundation of China

Corresponding author: Meng-han WANG; Tel: +86-13637957075; E-mail: cquwmh@163.com

DOI: 10.1016/S1003-6326(19)64986-1