DOI: 10.11817/j.issn.1672-7207.2018.09.009
外热式回转窑横截面内散体物料的传热特性
张喆1,刘义伦1, 2,赵先琼1,雷先明3
(1. 中南大学 机电工程学院,湖南 长沙,410083;
2. 中南大学 轻合金研究院,湖南 长沙,410083;
3. 邵阳学院 机械与能源工程系,湖南 邵阳,422004)
摘要:针对外热式回转窑横截面内散体物料传热问题,建立颗粒-筒壁导热、颗粒-颗粒导热的数学模型,使用离散元软件EDEM及二次开发工具C++对散体物料在滚落模式下的传热过程进行数值模拟,研究单个颗粒温度演化以及不同参数对物料传热特性的影响。研究结果表明:单个颗粒温度在平流层升温-活动层降温的循环中逐步升高,颗粒沿径向的“移位”现象对传热影响较大;加热过程中在散体物料内部存在“冷核”区域;转速不影响物料的平均温度,但影响物料温度分布的均匀性,转速越高,温度均匀性越好;填充率越小,物料平均温度越高,但物料温度的均匀性随着填充率变小呈现先减小后增大的趋势。
关键词:回转窑;外热式;散体物料;传热;离散单元法
中图分类号:TK124 文献标志码:A 文章编号:1672-7207(2018)09-2178-06
Heat transfer characteristics of granular materials in cross section of externally heated rotary kiln
ZHANG Zhe1, LIU Yilun1, 2, ZHAO Xianqiong1, LEI Xianming3
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. Research Institute of Light Alloy, Central South University, Changsha 410083, China;
3. Department of Mechanical and Energy Engineering, Shaoyang University, Shaoyang 422004, China)
Abstract: For the heat transfer problem of granular materials in the cross section of externally heated rotary kiln, the heat conduction mathematic models of particle-cylinder and particle-particle were established. The discrete element software (EDEM) and the secondary development tool (C++) were used to simulate the heat transfer process of granular materials in rolling mode. The temperature evolution of individual particle and the influence of different parameters on heat transfer characteristics of bulk materials were studied. The results show that the temperature of individual particle gradually increases in the cycle of plug flow heating and active layer cooling, and the “displacement” of particles in the radial direction has great influence on heat transfer. There is a “cold core” inside the bulk materials in the heating process. The rotating speed does not affect the average temperature of bulk materials, but affect the uniformity of the temperature distribution. The uniformity of temperature distribution becomes better with the increase of rotating speed. The average temperature of bulk materials increases as filling ratio decreases, but the uniformity of temperature tends to decrease first and then increase as the filling ratio becomes smaller.
Key words: rotary kiln; externally heated; granular materials; heat transfer; discrete element method
外热式回转窑是通过电加热、燃油加热等方式将热量通过壁面传递给物料的一种热工设备,主要用于颗粒物料的混合、干燥、分解、烧结等过程[1-4]。回转窑横向截面是物料层产生温度梯度,造成传热不均匀和传热效率低下的主要区域[5-8]。通过实验和数值计算,国内外学者对回转窑横向截面内物料传热特性开展了研究。朱立平等[9-13]分别通过实验手段测得回转窑物料内部温度,并建立了与实验数据相符的传热模型。在数值计算方面,由于物料呈现散体颗粒状,离散单元法成为研究回转窑内物料传热问题的有效工具。FIGUEROA等[14]研究了外热式滚筒内物料混合和传热的关系,NGUYEN等[15]研究了高分子聚合物粉末在回转窑横向截面内的运动规律和传热特性,EMADY等[16]建立了回转滚筒内颗粒与高温筒壁接触过程中的3种传热时间模型。在现有文献中,大部分侧重于整体物料传热特性的研究[17-21],对单个颗粒温度演化规律的报道还较少,对运行参数和物性参数影响物料传热的解释也不够充分。本文作者采用离散单元法对外热式回转窑横截面内物料传热过程进行数值模拟,研究单个颗粒的温度演化以及转速和填充率对物料传热特性的影响,以便为回转窑实际应用中最佳工况的改进提供参考。
1 建立传热模型
外热式回转窑横向截面热量传递过程包括颗粒-筒壁导热、颗粒-颗粒导热、颗粒-自由气体对流、颗粒-未接触筒壁辐射、颗粒-间隙气体导热。本文研究环境为近似真空的封闭筒体,即不考虑颗粒-自由气体对流;壁面温度相对较低(400 K),基本可以忽略辐射影响。当间隙气体热导率远小于颗粒热导率时,颗粒-间隙气体导热与前2种导热机制相比也可忽略不计[11, 16]。本文主要考虑在外热式回转窑横向截面内占据主导地位的颗粒-筒壁导热、颗粒-颗粒导热这2种传热机制。
热流在相互接触的颗粒-颗粒或者颗粒-筒壁之间传递可以用如下方程描述[11]:
 (1)
(1)
式中:Qij为颗粒j传递给颗粒i的热量;Ti和Tj分别为颗粒i和j的温度;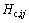 为颗粒i和j间的导热系数。
为颗粒i和j间的导热系数。
 (2)
(2)
式中:ks为颗粒热导率;FN为接触力的法向分量; 为接触部分的有效半径;
为接触部分的有效半径; 为颗粒的有效弹性模量。颗粒i的温度演变过程如下:
为颗粒的有效弹性模量。颗粒i的温度演变过程如下:
 (3)
(3)
式中: 为颗粒i的密度;ci为颗粒i的比热容;Vi为颗粒i的体积。
为颗粒i的密度;ci为颗粒i的比热容;Vi为颗粒i的体积。
根据式(1)~(3)可得单个颗粒与周围颗粒或筒壁接触后的温度改变量,从而能够得到整个物料层在任意时间的温度分布。
2 模型数值计算
选用的计算软件为EDEM,使用自定义的传热程序进行离散元模拟。筒体水平放置,筒壁作为恒温热源,端面为绝热表面,选择转速 和填充率f满足滚落模式要求。颗粒弹性模量、比热容、热导率等物性参数为常数,单个时间步长内颗粒内部不存在温度梯度,数值模拟参数设置如表1所示。模拟总时间为21 s,其中滚筒转动时间为20 s(第1 s用来产生颗粒)。
和填充率f满足滚落模式要求。颗粒弹性模量、比热容、热导率等物性参数为常数,单个时间步长内颗粒内部不存在温度梯度,数值模拟参数设置如表1所示。模拟总时间为21 s,其中滚筒转动时间为20 s(第1 s用来产生颗粒)。
表1 数值模拟参数
Table 1 Numerical simulation parameters

3 结果与分析
为研究单个颗粒温度随时间的变化规律,选择初始时间物料表层最右端颗粒为示踪颗粒,图1所示为示踪颗粒的运动轨迹。由图1可知:物料在回转窑横向截面的运动可以分为2个区域,即贴壁运动的平流层以及滚落运动的活动层。物料在平流层的运动轨迹为同心圆弧轨道,运动轨迹间无交叉;颗粒进入活动层后,运动轨迹出现跳跃和交叉,滚落后随机进入另一平流层轨道,如此不断循环,颗粒能运动至任意区域。

图1 示踪颗粒的运动轨迹
Fig. 1 Trajectory of tracer particle
图2所示为示踪颗粒温度随时间的变化曲线。颗粒从平流层上升吸热到活动层滚落散热为1个温度循环,结合图1与图2可知:示踪颗粒主要完成了4个温度循环,对应时间分别为1.0~7.0,7.0~12.6,12.6~16.9和16.9~19.4 s。
在1.0~5.6 s内,示踪颗粒随滚筒旋转从初始位置运动至物料斜面最高点。颗粒温度虽然总体上呈上升趋势,但温度并不是持续升高,相反地,期间出现了几次温度降低的情况,尤其在2.2~2.9 s时,温度急剧下降。由图1局部放大视图可以看出:颗粒沿平流层的运动轨迹并不是绝对平滑的曲线。这说明颗粒间存在间隙,其本身直径也不能忽略,颗粒在运动过程中与周围颗粒群产生接触和碰撞,造成颗粒产生小幅度“移位”,这种“移位”现象影响了颗粒传热情况。
颗粒在平流层的“移位”可分为沿圆周方向移动和沿半径方向移动,其中沿径向移动对颗粒传热有显著影响。当颗粒沿径向“移位”至靠近筒壁的相邻区域时,由于与更多高温颗粒接触,加热速度变快;当颗粒“移位”至远离筒壁的相邻区域时,与更多低温颗粒接触,加热速度变慢甚至出现散热现象。示踪颗粒在2.2,3.4与4.0 s对应的温度下降均是颗粒 “移位”至远离筒壁的相邻区域所致;在2.2 s时温度降低尤为明显,是因为“移位”现象使示踪颗粒与高温筒壁脱离接触,同时,周围颗粒由于未被加热还处于初始温度,巨大的温差使示踪颗粒温度骤降。
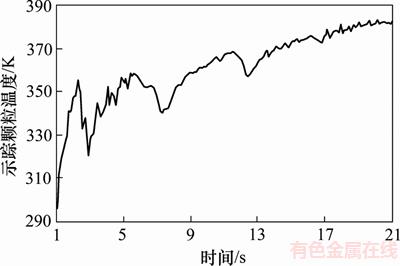
图2 示踪颗粒温度随时间的变化
Fig. 2 Temperature evolution of tracer particle over time
在5.6~7.0 s内,示踪颗粒从物料斜面最高点滚落。颗粒在滚落过程中产生能量损失,温度降低,由此完成了1个温度循环过程,之后随机进入另一平流层轨道开始下一个循环。随着颗粒群持续与高温筒壁接触吸收热量,示踪颗粒在平流层升温-活动层降温的循环过程中温度逐步升高,“移位”后加速加热或散热的效果逐渐减弱,最终与筒壁温度保持一致。
图3所示为物料在不同时间的温度分布。由图3可知:平流层贴壁运动的颗粒与高温筒壁接触吸收热量,温度逐渐升高,颗粒在运动至物料斜面顶端时温度最高,外层高温颗粒将热量逐步向中心低温区域传递,平流层颗粒温度根据距筒壁距离的不同呈现出明显的分层现象。
当颗粒到达斜面顶端后,由于摩擦力无法克服重力沿剪切面的分量而向下滚落,滚落的高温颗粒和相邻低温颗粒间由于接触和碰撞产生热量损失,在平流层高温颗粒与活动层高温颗粒包围区域内形成了1个“冷核”,“冷核”区域面积以及存在时间严重影响物料受热情况。可以预见:随着颗粒不断与高温筒壁接触,物料温度将逐渐升高,“冷核”区域逐渐减小。但只依靠延长加热时间来消除“冷核”区域,不仅造成能源浪费,还会产生过烧等不良现象,降低产物质量。
用颗粒群在每一时间的温度期望表示物料的整体温度,温度标准差表示物料内部温度的不均匀性。研究滚筒转速ω和填充率f对颗粒群温度期望和温度标准差的影响规律,选取的变量ω和f均符合滚落模式要求。

图3 不同时间物料温度分布
Fig. 3 Temperature distributions of particles at different time
图4(a)所示为不同转速下物料温度期望随时间的变化规律。由图4(a)可知:物料整体温度随颗粒与筒壁接触逐渐升高,升温速率逐渐减小,这是颗粒与滚筒温度差逐渐减小的缘故。转速对物料平均温度并无显著影响,这是由于在保持滚落的运动模式下,改变速度只改变物料贴壁运动的上升高度和滚落的斜面角度,对单个颗粒而言,会影响其随滚筒上升的加热时间和滚落的散热时间,但对于整体物料来说,每一时间与筒壁接触的传热面积基本不变,因此,平均温度并没有发生显著变化。可以预见:随着转速进一步提高,颗粒运动模式将发生改变,转速对物料平均温度的影响规律也会随之变化。
图4(b)所示为不同转速下物料温度标准差随时间的变化规律。由图4(b)可知:物料温度的不均匀性呈现先增大后减小的趋势。这是因为开始时贴壁运动的高温颗粒与内层低温颗粒的温差较大,随着颗粒持续与高温筒壁接触,颗粒温度逐步升高,同时混合也逐渐充分,物料温度分布的不均匀性逐步减小,最终物料温度与筒壁温度保持一致。滚筒转速对物料平均温度并无太大影响,但对物料温度分布均匀性影响显著,高转速可以促进颗粒混合,滚筒转速越高,物料温度分布的均匀性越好。
图5(a)所示为不同填充率下物料温度期望随时间的变化规律。与预期一样,填充率越小,物料平均温度越高,因为低填充率一方面会加快物料混合速度,另一方面会减少物料升温所需热量。

图4 不同转速下物料温度期望和标准差的变化
Fig. 4 Mean and standard deviation of particle temperature under different rotation speeds
图5(b)所示为不同填充率下物料温度标准差随时间的变化规律。由图5(b)可以看出:总体上看,填充率越小,物料达到目标温度的时间以及充分混合的时间越短,物料温度的均匀性越好;但在初始阶段有所异常,在初始的4 s内,物料温度均匀性随填充率的减小而降低,这是因为相比高填充率,颗粒个数减少,初始阶段高温颗粒所占比例增大,颗粒群温度标准差也随之增大。

图5 不同填充率下物料温度期望和标准差的变化
Fig. 5 Mean and standard deviation of particle temperature under different filling ratios
4 结论
1) 单个颗粒温度在平流层升温-活动层降温的循环中逐步升高,且由于存在“移位”现象,颗粒在平流层升温时还伴随局部的降温过程。
2) 在高温筒壁的加热过程中,平流层高温颗粒群与活动层高温颗粒群包围区域内形成“冷核”,“冷核”区域随加热时间逐渐减小。
3) 在滚落模式下,转速不影响物料平均温度,但影响物料温度分布的均匀性,转速越高,温度均匀性越好。
4) 在滚落模式下,填充率越小,物料平均温度越高,但物料温度的均匀性随着填充率变小呈现先减小后增大的趋势。
参考文献:
[1] 吴静, 李选友, 陈宝明, 等. 大颗粒低填充率外热式回转窑传热系数模型的构建[J]. 农业工程学报, 2014, 30(13): 256-262.
WU Jing, Li Xuanyou, CHEN Baoming, et al. Development of heat transfer coefficient model for external heated rotary kiln with low filling large particles[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(13): 256-262.
[2] 陈辉, 刘义伦, 赵先琼, 等. 一元散体颗粒物料在回转窑截面上的运动与混合[J]. 中国有色金属学报, 2015, 25(5): 2575-2581.
CHEN Hui, LIU Yilun, ZHAO Xianqiong, et al. Motion and mixing of mono-disperse granular material in cross section of rotary kiln[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(5): 2575-2581.
[3] 王瑞芳, 李占勇, 窦如彪, 等. 水平转筒内大豆颗粒随机运动与混合特性模拟[J]. 农业机械学报, 2013, 44(6): 93-99.
WANG Ruifang, LI Zhanyong, DOU Rubiao, et al. Simulation on random motion and mixing characteristic for soybean in rotary drum[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(6): 93-99.
[4] 孙立军,刘柏谦,谭培来,等. 滚筒冷渣机料床温度分布及传热性能研究[J]. 动力工程学报, 2015, 35(7): 568-573.
SUN Lijun, LIU Boqian, TAN Peilai, et al. Study on bed temperature distribution and heat transfer performance of rotary drum ash coolers[J]. Journal of Chinese Society of Power Engineering, 2015, 35(7): 568-573.
[5] BOATENG A A, BARR P V. A thermal model for the rotary kiln including heat transfer within the bed[J]. International Journal of Heat and Mass Transfer, 1996, 39(10): 2131-2147.
[6] DEMAGH Y, MOUSSA H B, LACHI M, et al. Surface particle motions in rotating cylinders: validation and similarity for an industrial scale kiln[J]. Powder Technology, 2012, 224: 260-272.
[7] GUI Nan, YAN Jie, XU Wenkai, et al. DEM simulation and analysis of particle mixing and heat conduction in a rotating drum[J]. Chemical Engineering Science, 2013, 97: 225-234.
[8] GENG Fan, LI Yiming, WANG Xinyong, et al. Simulation of dynamic processes on flexible filamentous particles in the transverse section of a rotary dryer and its comparison with ideo-imaging experiments[J]. Powder Technology, 2011, 207(1/2/3): 175-182.
[9] 朱立平, 秦霞, 袁竹林, 等. 丝状颗粒在滚筒横向截面中的传热传质特性[J]. 东南大学学报(自然科学版), 2014, 44(4): 756-763.
ZHU Liping, QIN Xia, YUAN Zhulin, et al. Heat and mass transfer characteristics of filamentous particles in transverse section of rotary dryer[J]. Journal of Southeast University (Natural Science Edition), 2014, 44(4): 756-763.
[10] LIU Xiaoyan, SPECHT E. Temperature distribution within the moving bed of rotary kilns: measurement and analysis[J]. Chemical Engineering and Processing: Process Intensification, 2010, 49(2): 147-150.
[11] CHAUDHURI B, MUZZIO F J, TOMASSONE M S. Experimentally validated computations of heat transfer in granular materials in rotary calciners[J]. Powder Technology, 2010, 198(1): 6-15.
[12] KOMOSSA H, WIRTZ S, SCHERER V, et al. Heat transfer in indirect heated rotary drums filled with monodisperse spheres: comparison of experiments with DEM simulations[J]. Powder Technology, 2015, 286: 722-731.
[13] THAMMAVONG P, DEBACQ M, VITU S, et al. Experimental apparatus for studying heat transfer in externally heated rotary kilns[J]. Chemical Engineering & Technology, 2011, 34(5): 707-717.
[14] FIGUEROA I, VARGAS W L, MCCARTHY J J. Mixing and heat conduction in rotating tumblers[J]. Chemical Engineering Science, 2010, 65(2): 1045-1054.
[15] NGUYEN H T, COSSON B, LACRAMPE M F, et al. Numerical simulation on the flow and heat transfer of polymer powder in rotational molding[J]. International Journal of Material Forming, 2015, 8(3): 423-438.
[16] EMADY H N, ANDERSON K V, BORGHARD W G, et al. Prediction of conductive heating time scales of particles in a rotary drum[J]. Chemical Engineering Science, 2016, 152: 45-54.
[17] SHI D, VARGAS W L, MCCARTHY J J. Heat transfer in rotary kilns with interstitial gases[J]. Chemical Engineering Science, 2008, 63(18): 4506-4516.
[18] YOHANNES B, EMADY H, ANDERSON K, et al. Scaling of heat transfer and temperature distribution in granular flows in rotating drums[J]. Physical Review E, 2016, 94(4): 1-5.
[19] KWAPINSKA M, SAAGE G, TSOTSAS E. Continuous versus discrete modelling of heat transfer to agitated beds[J]. Powder Technology, 2008, 181(3): 331-342.
[20] SCHMIDT R, NIKRITYUK P A. Numerical simulation of the transient temperature distribution inside moving particles[J]. The Canadian Journal of Chemical Engineering, 2012, 90(2): 246-262.
[21] INGRAM A, SEVILLE J P K, PARKER D J, et al. Axial and radial dispersion in rolling mode rotating drums[J]. Powder Technology, 2005, 158(1/2/3): 76-91.
(编辑 刘锦伟)
收稿日期:2017-10-21;修回日期:2017-12-17
基金项目(Foundation item): 国家自然科学基金资助项目(51374241,51275531);湖南省教育厅重点研究项目(17A194) (Projects(51374241, 51275531) supported by the National Natural Science Foundation of China; Project(17A194) supported by the Scientific Research Project of Department of Education of Hunan Province)
通信作者:刘义伦,博士,教授,从事离散物质传热传质机理研究;E-mail: ylliu@csu.edu.cn