Semi analytical modeling of springback in

arc bending and effect of forming load

S. K. PANTHI, N. RAMAKRISHNAN

Advanced Materials and Processes Research Institute (AMPRI), Bhopal-26 (MP), India

Received 14 December 2010; accepted 20 March 2011

Abstract: The analytical model for springback in arc bending of sheet metal can serve as an excellent design support. The amount of springback is considerably influenced by the geometrical and the material parameters associated with the sheet metal. In addition, the applied load during the bending also has a significant influence. Although a number of numerical techniques have been used for this purpose, only few analytical models that can provide insight into the phenomenon are available. A phenomenological model for predicting the springback in arc bending was proposed based on strain as well as deformation energy based approaches. The results of the analytical model were compared with the published experimental as well as FE results of the authors, and the agreement was found to be satisfactory.

Key words: springback; sheet metal bending; finite element simulation; analytical modeling

1 Introduction

Sheet metal bending process plays a major role in automobile and aerospace industries to manufacture curved parts, in the construction of large spherical and cylindrical pressure vessels, etc. One of the major design problems in any sheet metal forming process is associated with springback. Springback in sheet metal parts after forming causes deviation of the final product from the targeted dimensions due to elastic recovery leading to difficulties in the fabrication of structures.

The elastic recovery is influenced by a combination of various process parameters such as tool shape and dimension, material properties, thickness of the sheet, type of the process. Accurate prediction of the springback after a forming operation is of vital importance in the design of tools. Presently, the prediction of springback is largely based on numerical FE simulation [1-13]. FEM is a time-consuming, expensive method and also very sensitive to numerical parameters [14-15], such as element type and size, algorithms, contact definition and convergence criteria for solution. Above all, FEM does not provide insight similar to that of analytical expressions. Therefore, it was desired to develop a simple analytical model, so as    to facilitate better understanding of the springback

prediction.

The prediction of springback in bending operation has been carried out by many investigators in the past. For instance, XUE et al [14] presented an energy based theoretical approach which employed the membrane theory of shells and was mainly focused on the deformation and springback of circular and square plates subjected to hemispherical stamping. ZHANG et al [15] presented an analytical model to predict the springback in ‘V’ bending considering combined hardening coefficient, blank holder force, sheet thickness etc. PERDUIJN and HOOGENBOOM [16] derived an explicit relation for the bending couple curvature for elastic-elasto plastic, elastic-rigid plastic and rigid plastic model. MORESTIN et al [17] developed a mechanical theory and implemented in a code to predict the final shape of a product in deep drawing process. WEI and WAGONER [18] presented a method for the design of sheet metal forming dies taking into account the springback. The method was an iterative technique based on comparing the shape of a target part with the formed as well as the unloaded parts. TEKINER [19] carried out an experimental study on the determination of springback on bent products. The amount of springback of several sheet metals with different bending angles was obtained on ‘V’ bending dies. ZHANG and LIN [20] developed an analytical model to study the springback in sheet metal stamps with a rigid punch and an elastic die. They discussed the dependence of springback on the main stamping parameters in detail. ASNAFI [21] developed an analytical model for ‘V’-die air bending to predict the springback and fracture in thick stainless steel sheets. CHAKRABARTY et al [22] developed a relationship between the bending couple and the curvature of the bent sheet and studied the influence of anisotropy and strain hardening on the bending characteristic of the sheet metal. TAN et al [23] developed a model for sheet bending and studied the effect of anisotropy and Bauschinger effect on the thinning in the sheet. DADRAS [24] analyzed an elastic-plastic plane strain pure bending using linear hardening material. ZHANG [25] et al developed an analytical model for the prediction of springback in plane strain U-bending based on Hill 48 yield criterion with different hardening rule, i.e. kinematic, isotropic and combined hardening. YI et al [26] developed analytical models based on residual differential strain and bending moment to calculate springback in sheet metal bending. GAU and KINZEL [27] proposed an incremental method and hardening model based on the isotropic hardening, kinematic hardening, Morz multiple surface model, and considered Bauschinger effect to predict the springback in plane strain bending. GAU and KINZEL [28] developed a model based on isotropic and kinematic models, Morz multiple surface model for springback prediction of aluminum sheet forming. POURBOGHRAT and CHU [29] described a method to predict springback in two-dimensional draw bending operation using moment curvature relationships and incorporate kinematic hardening in unbending. POURBOGHRAT et al [30] developed the hybrid membrane/shell method to predict springback of anisotropic sheet metals undergoing axisymmetric loading. ANOKYE-SIRIBOR and SINGH [31] used parabolic straight theory to develop analytical model for the air bending process. EL-DOMIATY and ELSHARKAWY [32] introduced a model for stretch bending in U-section beam which is capable of determining the effect of beam cross section and material property, forming load and final shape. ZHAO and LEE [33] simulated springback using a combined kinmatic/isotropic hardening model in draw bend. KIM et al [34] considered the material properties and realistic non-linear curvature of the bent sheet to develop the analytical model for springback prediction in air bending. POURBOGHRAT et al [35] developed a hybrid membrane/shell method using Hill’s 1948 yield criterion along with normal anisotropy along with kinematic and isotropic hardening laws during reverse loading.

Analytical solutions have been presented by many investigators in the past for U- as well as V-bending, automotive sheet etc [12-16, 36-37]. However, less attention has been paid to regarding the design of components used in the fabrication of large cylindrical and spherical structures for thick sheets considering the effect of forming load on springback. In this investigation, an analytical model is proposed to predict the springback in arc bending. The model is developed considering the average strain throughout the thickness of the sheet and taking into account the effect of load on plane stress and plane strain. The analytical model is based on two different approaches: one based on strain and the other on deformation energy. This model is applied to the arc bending problem and the predicted results are compared with the results of FE simulation as well as the published experimental ones [38]. The elasto- plastic FE analysis of sheet metal bending process is carried out using inhouse developed software (RRL-FEM). RRL-FEM is based on a large deformation algorithm. The constitutive relation used in the code is based on a total-elastic- incremental-plastic (TEIP) strain [39]. The validity of the code as well as the constitutive framework has been described elsewhere [39]. The TEIP algorithm is specially capable of handling the elastic unloading accurately.

2 Analytical modeling of arc bending

2.1 Assumptions

The following assumptions are made in the modeling:

1) Material is isotropic and homogeneous.

2) There is no residual stress in the sheet prior to, or after the bending.

3) Bending conforms to cylindrical surface.

4) Neutral axis remains at the mid section of the sheet during bending and is tensile strain free.

2.2 Tangential and radial strain

The radii of the bent sheet at the neutral layer, the inner surface and the outer surface are r, r_I and r_O respectively, as shown in Fig. 1. The arc lengths are , and , respectively, where q is the angle subtended at the center of the circle. The neutral layer is assumed to be free from the tangential strain. The tangential strain (e_O) at the outer surface (convex) of the bent sheet can be written as e _O=

. Since , where t is the thickness of the sheet.

                                    (1)

Similarly, the compressive strain (e_I) at the inner surface (concave) of the bent sheet can be written as:

                                   (2)

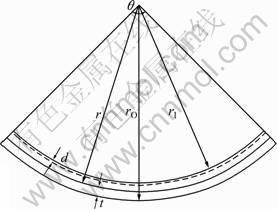
Fig. 1 Geometry used for analytical modeling

An FE simulation was performed to verify Eqs. (1) and (2) and the details are presented in section 4. The magnitude of the average strain across the tensile region from the neutral layer to the outer surface of the bent sheet can be shown to be α_O=t/4r and the compression region to be α_I=-t/4r. The radial strain in the compressed sheet due to the platen depression is given by β=-d/t, where d is the compression depth, i.e., the reduction in the thickness of the sheet due to the platen depression.

2.3 Plane stress condition

2.3.1 Effective strain

The following strains are experienced at the outer tensile region of the bent sheet.

The tangential strain,

                                (3)

The radial strain,

                         (4)

And the strain in z (width) direction,

                              (5)

The effective strain  is given in Refs. [39-40]:

     (6)

Substituting Eqs. (3), (4) and (5) in Eq. (6) get the effective strain at the outer tensile region of the bent sheet to be

                         (7)

Similarly, the effective strain at the inner compressive region of the bent sheet can be shown to be

                         (8)

Taking α= α_O=-α_I=t/4r, averaging the effective strain across the entire cross section (Eqs. (7) and (8)), we get

                                (9)

2.3.2 Springback

In this case, the sheet bent to the desired radius with the platen induced compression is considered. Let us use subscript ‘i’ to denote the initial condition.

Considering α_i=t/4r_i and β_i=-d/t, it can be shown using Eq. (9) that

                          (10)

Let us use subscript ‘f’ to denote the final condition, where the sheet is free from any load. Considering α_f=t/4r_f and β_f=(d/t)_p1, where r_f is the radius of the bent sheet after the springback and β_f is the irrecoverable compressive plastic strain, we have

                 (11)

2.3.3 Strain based approach

Equating the difference between the initial and the final effective strains to the deformation induced elastic strain (e), we get

                                 (12)

Here

                              (13)

where  represents the flow curve of the material. Here, E is the elastic modulus, A is a material constant and n is the strain-hardening exponent. Substituting and  from Eqs. (10) and (11) in Eq. (12), and simplifying and rearranging, we get

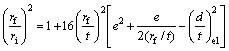        (14)

here  corresponds to the elastic component of the compressive strain, a term that gets limited by the expression’s domain of applicability as given below:

where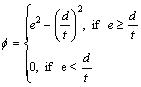

The choice of f depends on the energy consideration and is explained in the following section.

2.3.4 Energy based approach

Equating the difference between the initial and the final deformation energies to the elastic strain energy input during the bending,

                               (15)

We can show in the previous section,

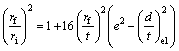               (16)

As we can see from Eq. (16), a negative value of f is not energetically permissible and takes a value as given in Eq. (14).

2.4 Plane strain condition

The derivation is similar to the one given in section 2.3 and the details are presented in the appendix.

For strain based approach, the springback value turns out to be

             (17)

where .

For energy based approach,

                        (18)

where

3 Numerical modeling

3.1 Modeling of die

In this study, the FE simulation of bending, involving both the die and the punch, was modeled as an arc of a simple circular curve of a specified sector angle, as shown in Fig. 2. The numerical difficulties were experienced due to the presence of sharp corner at the end of the die during the simulation. Numerically, it was difficult to slide the nodes of the deforming body (sheet) at the sharp corners of the rigid die. To overcome this shortcoming, the die was modeled as combination of two reverse circular curve joints at a common tangent point, as shown in Fig. 2 (at point marked as A).

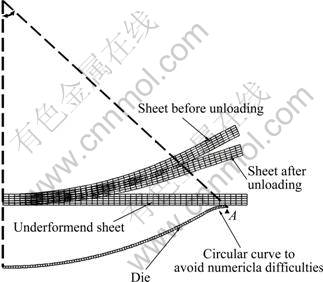
Fig. 2 Bending process showing initial, loaded and unloaded sheet

3.2 Material modeling

The following power law equation is used to represent the flow of the material during the process.

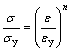                               (19)

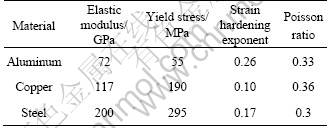
where n is the strain-hardening exponent,  and  are respectively the stress and the strain corresponding to yield condition. The mechanical properties used in the study are presented in Table 1 [41-43].

Table 1 Mechanical properties of materials

3.3 Constitutive relation used in finite element software (RRL-FEM)

The constitutive relation for large deformation [39], based on additive decomposition of velocity strains into elastic and plastic components that relates Cauchy stress to the total-elastic-incremental-plastic (TEIP) strain assuming J₂ plasticity, is used. TEIP algorithm directly incorporates the material rotation in the constitutive equation without any trigonometric approximations, as done in Jaumann rate etc [40]. This allows large rotation to be simulated with a reasonable accuracy. In addition, the total elastic strain that always appears in the main constitutive equation makes the unloading calculation reliable and more accurate.

3.4 Mesh geometry and boundary condition

The initial geometry used for the simulation, with an FE mesh, is shown in Fig. 2. A software, coded in FORTRAN, is developed to generate the FE mesh. The thickness of the sheet, the radius of the die, the number of elements in the sheet in x- and y-direction, the number of elements in the die and the punch, and the sector angle are used as input to generate the mesh. The initial mesh configuration consists of bilinear quadrilateral elements, as shown in Fig. 2. The details can be found in Ref. [13].

3.5 Numerical simulation

In the simulation, the sheet is placed on the bottom die and the punch is moved downward gradually. Once the punch senses the contact, the deformation is induced in the sheet and the sheet metal bends gradually. This is numerically simulated by assigning the necessary total punch displacement but is carried out in about thousand increments. Figure 2 shows the deformation of sheet at various stages of the process. The springback is predicted in terms of the springback ratio from minimal load condition to different extent of compression. It can also be taken as different levels of permanent plastic strain induced in the sheet. In this study, the ‘minimal load condition’ refers to the depression of the punch at which the sheet metal just takes the shape of the die. Any subsequent displacement of the punch from the minimal load condition increases the load, which will finally saturates the springback [13] at some point. After the complete depression, the punch is gradually elevated to free the plate and plate is allowed to elastically relax itself incrementally and iteratively. The final shape of the bent sheet after releasing the load of forming is shown in Fig. 2 by FEA. The springback is calculated in terms of the change in radius, i.e., the difference between the initial and the final radii.

4 Results and discussion

This discussion essentially pertains to the analytical modeling but the validation of the FE simulation is presented elsewhere [13]. The analytical model basically rests with the assumption that there is no significant net residual stress in the sheet. This is possible only when the compressive strain in the inner concave region is compensated by the tensile strain in the outer convex region where the neutral radius is assumed to be tangential strain free. In the model, this assumption leads to strain varying linearly from -t/2r to t/2r  (Eqs. (1) and (2)) from the concave (inner) to the convex (outer) surface of the bent sheet. The neutral layer remains at the mid section of the sheet. The bent sheet (before loading) and the final component (after unloading) are assumed to conform to a sector of a circle, as shown in Fig. 1. This aspect of circularity and the strain variation from -t/2r to t/2r have been specially verified using the FE simulation in this investigation.

The expressions for calculating the springback ratio based on the strain based approach and the energy based approach are presented by Eqs. (14) and (16) for plane stress condition, and Eqs. (17) and (18) for plane strain condition, respectively. The springback ratio essentially depends on the elastic strain e, normalized design radius r_f/t and the extent of loading corresponding to d/t. The springback expectedly increases with increase in the deformation induced elastic strain and it decreases with the compression load. The ratio r_f/t has a greater influence at lower forming loads, but this effect gets almost nullified with increase in load.

A comparison is made between the analytical model and a few published experimental data for copper along with the results of the FE simulation in Fig. 3. FE based plane stress results match well with the published experimental ones. The abscissa is taken as r_f/t for design convenience since the input to the designer is given in terms of final radius of the bent sheet. In Fig. 3, the results are plotted for the minimal load condition. Figure 4 shows the comparison of analytical results (plane  stress) based on the strain as well as the energy based approaches with FE simulation and published experimental data [38] for copper, aluminum and steel, respectively. It emerges from these plots that the results of the strain based approach are in better agreement with the FE simulation and the experimental results compared to the results of the energy based approach. The strain based approach heuristically corresponds to force equilibrium and naturally provides upper bound solution, while the energy based approach corresponds to energy conservation and leads to the lower bound solution.

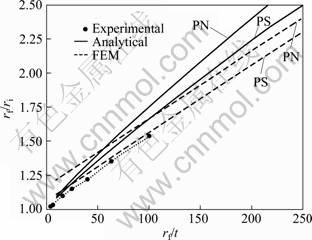
Fig. 3 Comparison of analytical model as well as FE simulation under plane strain (PN) and plane stress (PS) conditions by strain based approach (Eqs. (14) and (16)) with published experimental results for copper [38]

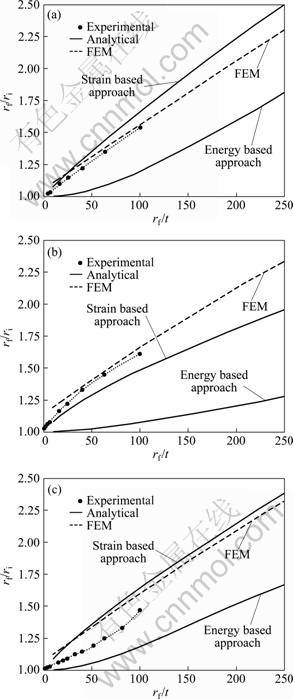
Fig. 4 Comparison of analytical model as well as FE simulation with published experimental results [38] for copper (a), aluminum (b) and steel (c)

Based on the above conclusion, the effect of load is carried out for the strain based approach. Graphs are plotted between the springback ratio r_f/r_i  and the design ratio r_f/t  for different d/t values for copper, aluminum and steel sheet material, as shown in Fig. 5. The results of the present analytical model are in reasonable agreement with the results of the FE simulation for all the three materials in the range of 0f/t<250. The springback ratio increases with increase in the ratio of r_f/t for the minimal load conditions but saturates to a thin band for higher loads. Springback ratio is observed to be higher by the analytical models as compared with FE results which may be due to the assumption of zero residual stress. A plot between the springback ratio and d/t for different r_f/t  values is shown in Fig. 6 for copper, aluminum and steel sheet respectively to clearly bring out the effect of load.

Fig. 4: Comparison of analytical, FE simulation and published experimental [38] results for (a) Copper (b) Aluminum and (c) Steel

  Fig. 5 Comparison of effects of load on springback by analytical model and FE simulation for different ratio values of compression depth (d) to thickness (t) for copper (a), aluminum (b) and steel (c)

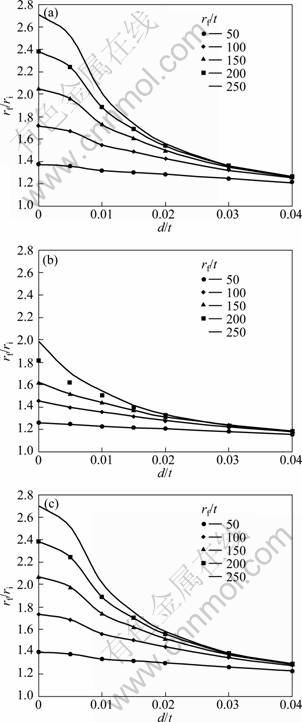
Fig. 6 Effect of load on springback by analytical model for different radii of die for copper (a), aluminum (b) and steel (c)

5 Conclusions

1) Analytical models were developed to predict the springback in arc bending, specially taking into account the effect of load under plane stress (PS) and plane strain (PN) conditions. These equations provide insight into the dependence of springback ratio on the deformation induced elastic strain, the design ratio r_f/t  (ratio of final radius of the bent sheet after springback to thickness of the sheet) and the extent of loading dictated by d/t (ratio of the compression depth to the thickness of the sheet).

2) There is virtually no effect of r_f/t at the higher loads but it has a significant effect at the lower loads of forming. At higher loads, the springback ratio saturates to a near constant value for the entire range of r_f/t.

3) Strain as well as energy based approaches were used in the modeling indirectly corresponding to the force equilibrium (upper bound) and energy conservation (lower bound) respectively. Strain based approach is found to be in better agreement with the published experimental results and FE simulation.

4) The results of the plane stress and the plane strain conditions are affected only by a small factor  for a wide range of the Poisson’s ratio and the springback ratio is affected only to an extent of about 5%.

Appendix

Al effective strain on surface

The following strains are experienced at the outer tensile region of the bent sheet.

The tangential strain:

                    (a1)

The radial strain:

                     (a2)

And the strain in z (width) direction:

                                     (a3)

Substituting Eqs. (a1), (a2) and (a3) in Eq. (6), we get the effective strain at the outer tensile region of the bent sheet to be

    (a4)

Similarly, the effective strain at the inner compressive side of the bent sheet can be derived as:

    (a5)

Taking  and averaging the effective strain across the entire cross section, we get

                     (a6)

For strain based approach,

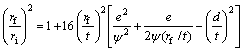     (a7)

where .

and

For energy based approach,

              (a8)

where w has the meaning as given in Eq. (a7).

References

[1] Cho J R, Moon S J, Moon Y H, Kang S S. Finite element investigation on springback characteristics in sheet metal U-bending process [J]. J Material Processing Technology, 2003, 141(1): 109-116.

[2] Livatyali H, Kinzel G L, Altan T. Computer aided die design of straight flanging using approximate numerical analysis [J]. J Material Processing Technology, 2003, 142: 532-543.

[3] Esat V, Darendeliler H, Gokler M I. Finite element analysis of springback in bending of aluminum sheets [J]. Materials and Design, 2002, 23: 223-229.

[4] Samuel M. Experimental and numerical prediction of springback and side wall curl in U-bending of anisotropic sheet metals [J]. J Material Processing Technology, 2000, 105: 382-393.

[5] Math M, Grizelj B. Finite element approach in the plate bending process [J]. J Material Processing Technology, 2002, 125-126: 778-784.

[6] Li X C, Yang Y Y, Wang Y Z, Bao J, Li S. Effect of the material-hardening mode on the springback simulation accuracy of V-free bending [J]. J Material Processing Technology, 2002, 123: 209-211.

[7] Chou I N, Hung C. Finite element analysis and optimization on springback reduction [J]. Int J Machine Tools & Manufacture, 1999, 39: 517-536.

[8] Lei L P, Hwang S M, Kang B S. Finite element analysis and design in stainless steel sheet forming and its experimental comparison [J]. J Material Processing Technology, 2001, 110: 70-77.

[9] Papeleux L, Ponthot J P. Finite element simulation of springback in sheet metal forming [J]. J Material Processing Technology, 2002, 125-126: 785-791.

[10] Taylor L, Cao J, Karafillis A P, Boyce M C. Numerical simulations of sheet metal forming [J]. J Material Processing Technology, 1995, 50: 168-179.

[11] Livatyali H, Wu HC, Altan T. Prediction and elimination of springback in straight flanging using computer-aided design methods (part 2): FEM predictions and tool design [J]. J Material Processing Technology, 2002, 120: 348-354.

[12] XU Feng, liN Zhong-qin, LI Shu-hui. Study on the influences of geometrical parameters on the formability of stretch curved flanging by numerical simulation [J]. J Material Processing Technology, 2004, 145: 93-98.

[13] Panthi S K, Ramakrishnan N, Pathak K K, Chouhan J S. An analysis of springback in sheet metal bending using finite element method (FEM) [J]. J Material Processing Technology, 2007, 186: 120-124.

[14] Xue P, Yu T X, Chu E. Theoretical prediction of the springback of metal sheets after a double-curvature forming operation [J]. J Material Processing Technology, 1999, 89–90: 65–71.

[15] Zhang Dong-juan, CUI Zhen-shan, RUAN Xue-yu, Li Yu-qiang. An analytical model for predicting springback and side wall curl of sheet after U-bending [J]. Computational Materials Sciences, 2007, 38: 707-715.

[16] Perduijn A B, Hoogenboom S M. The pure bending of sheet[J]. J Material Processing Technology, 1995, 51: 274-295.

[17] Morestin F, Boivin M, Silva C. Elasto plastic formulation using a kinematic hardening model [J]. J Material Processing Technology, 1996, 56: 619-630.

[18] Wei G, Wagoner R H. Die design method for sheet springback [J]. Int J Mechanical Sciences, 2004, 46: 1097-1113.

[19] Tekiner Z. An experimental study on the examination of springback of sheet metals with several thicknesses and properties in bending dies [J]. J Material Processing Technology, 2004, 145: 109–117.

[20] Zhang L C, Lin Z. An analytical solution to springback of sheet metals stamped by a rigid punch and elastic die [J]. J Material Processing Technology, 1997, 63: 49-54.

[21] Asnafi N. Springback and fracture in v-die air bending of thick stainless steel sheets [J]. Materials & Design, 2000, 21: 217-236.

[22] Chakrabarty J, Lee W B, Chan K C. An exact solution for the elastic/plastic bending of anisotropic sheet metal under conditions of plane strain [J]. Int J Mechanical Sciences, 2001, 43: 1871-1880.

[23] Tan Z, Persson B, Magnusson C. Plastic bending of anisotropic sheet metals [J]. Int J Mechanical Sciences, 1995, 37: 405-421.

[24] Dadras P. Plane strain elastic plastic bending of a strain hardening curved beam [J]. Int J Mechanical Sciences, 2001, 43: 39-56.

[25] ZHANG Dong-juan, cui Zhen-shan, ruan Xue-yu, li Yu-qiang. An analytical model for predicting springback and side wall curl of sheet after U-bending [J]. Computational Materials Sciences, 2007, 38: 707-715.

[26] Yi H K, Kim DW, Tyne C J V, Moon Y H. Analytical prediction of springback based on residual differential strain during sheet metal bending [J]. J Mechanical Engineering Sciences, 2008, 222: 117-129.

[27] Gau J T, Kinzel G L. A new model for springback prediction in which the Bauschinger effect is considered [J]. Int J Mechanical Sciences, 2001, 43: 1813-1832.

[28] Gau J T, Kinzel G L. A new model for springback prediction for aluminum sheet forming [J]. ASME, 2005, 127: 279-288.

[29] Pourboghrat F, Chu E. Springback in plane strain stretch/ draw sheet forming [J]. Int J Mechanical Sciences, 1995, 36: 327-341.

[30] Pourboghrat F, Karabin M E, Becker R C, Chung K. A hybrid membrane/shell method for calculating springback of anisotropic sheet metals undergoing axisymmetric loading [J]. Int J Plasticity, 2000, 16: 677-700.

[31] Anokye-Siribor K, Singh U P. A new analytical model for pressbrake forming using in-process identification of material characteristics [J]. J Materials Processing Technology, 2000, 99: 103-112.

[32] EL-Domiaty A A, Elsharkawy A A. Stretch-bending analysis of U-section beams [J]. Int J Math Tools Manufacturing, 1998, 38: 75-95.

[33] Zhao K M, Lee J K. Material properties of aluminum alloy for accurate draw-bend simulation [J]. ASME, 2001, 123: 287-292.

[34] Kim H, Nargundkar N, Altan T. Prediction of bend allowance and springback in air bending [J]. ASME, 2007, 129: 129-351.

[35] Pourboghrat F, Chung K, Richmond O A. Hybrid membrane/shell method for rapid estimation of springback in anisotropic sheet metals [J]. ASME, 1998, 65: 671-684.

[36] Chung K, Lee M G, Kim D, Kim C, Wenner M L, Barlat F. Springback evaluation of automotive sheets based on isotropic-kinematic hardening laws and non quadratic anisotropic yield functions Part I: theory and formulation [J]. Int J Plasticity, 2005, 21: 861-882.

[37] Lee M G, Kim D, Kim C, Wenner M L, Wagoner R H, Chung K. Springback evaluation of automotive sheets based on isotropic-kinematic hardening laws and non quadratic anisotropic yield functions (Part II): Chararacterization of material properties [J]. Int J Plasticity, 2005, 21: 883-914.

[38] Lange K. Handbook of metal forming [M]. New York: Mc-Graw Hill Book Company, 1985.

[39] Ramakrishnan N, Singh K M, Suresh R K V, Srinivasan N. An algorithm based on total-elastic- incremental-plastic strain for large deformation plasticity [J]. J Material Processing Technology, 1999, 86: 190-199.

[40] Malvern E. Introduction to the mechanics of a continuous medium [M]. NJ: Prentice-Hall Englewood Cliffs, 1969.

[41] American Society of Metals. Properties and selection; Nonferrous alloys and pure metals [M]. 9th ed. Materials Park, OH, 1979.

[42] American Society of Metals. Properties and selection; Irons, steels, and high performance alloys [M]. 10th ed. Materials Park, OH, 1990.

[43] American Society of Metals. Aluminum and aluminum alloys [M]. Materials Park, OH, 1998.

弯曲回弹的半解析建模及弯曲载荷的影响

S. K. PANTHI, N. RAMAKRISHNAN

Advanced Materials and Processes Research Institute (AMPRI), Bhopal-26 (MP), India

摘 要：对金属板材弧形弯曲的回弹建立解析模型可以为设计提供很好的支持。金属板材的几何形状和材料参数对回弹量的影响大；另外，弯曲载荷的影响也较大。许多数值模拟技术已经被用来预测回弹量，但只有少数的解析模型可以用来进行深入研究。为了预测弧形弯曲的回弹，基于应变以及变形能为基础的方法，提出了一个唯象模型；并对该解析模型的预测结果与已发表的实验结果以及采用有限元分析的结果进行比较。结果表明，他们的一致性很好，是令人满意的。

关键词：回弹；板料弯曲；有限元仿真；解析建模

(Edited by YANG Hua)

Corresponding author: S. K. PANTHI; Tel: +91-755-2457615; Fax: +91-755-2457042; E-mail: sanjay_panthi@yahoo.co.in; ramkrish@sify.com

DOI: 10.1016/S1003-6326(11)61008-X