DOI: 10.11817/j.issn.1672-7207.2015.01.009
基于数值模拟和响应面法的级进模成形优化
李军超1,王宾1,周同贵1,戴洪1,陆俊江2
(1. 重庆大学 材料科学与工程学院,重庆,400044;
2. 格力电器(重庆)有限公司,重庆,400039)
摘要:针对级进模成形件存在的起皱、破裂和成形精度低等质量缺陷,以某阀门支架零件为研究对象,采用多工步多工序的建模方法建立级进模成形全工序有限元模型。该模型可继承已成形工步的变形、应力等信息,并能够分析相邻工步变形的相互影响。以最大减薄率、最大增厚率和导正孔移动量作为优化目标,以压边力、摩擦因数、凸凹模间隙为设计变量,给出一种用于控制优化级进模成形件质量的数学模型;结合响应面法将此优化模型用于该阀门支架零件级进模成形参数的优化,得到质量缺陷最小化的成形参数组合。研究结果表明:采用该方法所得数值模拟结果与实际生产试制结果相吻合,无起皱和破裂缺陷,表明该优化方法是可行的,可有效指导级进模成形零件的产品质量控制。
关键词:级进模成形;全工序有限元模型;质量控制模型;响应面法;参数优化
中图分类号:TG386 文献标志码:A 文章编号:1672-7207(2015)01-0066-07
Progressive die forming optimization based on numerical simulation and response surface method
LI Junchao1, WANG Bin1, ZHOU Tonggui1, DAI Hong1, LU Junjiang2
(1. College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China;
2. Gree Electric Appliances (Chongqing) Co., Ltd., Chongqing 400039, China)
Abstract: Ruptures, winkles and low forming accuracy are the forming defects for progressive die forming parts. Based on valve bracket, a finite element model (FEM) of complete progressive die forming was established with a multi-step and multi-process modeling approach. In this way, the numerical model is able to inherit the simulation results of the former steps such as deformation and stress data, and the interaction between the adjacent forming steps were analyzed. Further, a model for controlling and optimizing the quality of the progressive die forming part was proposed. In this model, the maximum thinning ratio, the maximum thickening ratio and the amount of pilot hole movement were the optimization goals, while blank holder force, friction factor and the clearances between punch and die were the designed variables. Then, the forming parameters were optimized by using this quality control model in combination with the response surface method (RSM). The results show that the production trial results have no wrinkling and rupture defects and are in accordance with the numerical results, which indicates that the proposed optimization method is feasible and can provide an effective guidance for the product quality control in the progressive die forming.
Key words: progressive die forming; FEM model of complete process; quality control model; response surface method; parameter optimization
级进冲压成形除了易出现起皱和破裂等缺陷,成形精度也是其需要考虑的重要问题,这些缺陷主要受摩擦润滑条件、压边力、模具几何形状、材料特性等设计变量的影响[1]。虽然传统的工艺分析及模具设计已开始利用CAE技术进行模拟仿真,但选出的参数组合具有偶然性且无法保证其最优化,而挑选参数过程耗时长,无法适应现代工业的需要[2]。近年来,随着有限元模拟技术、优化理论的逐渐成熟和计算机技术的快速发展,以有限元分析工具并结合优化算法来提高板料的成形性能已成为国际上许多学者研究的前沿课题。Breitkopf等[3]运用移动的最小二乘法构造了一个连续的响应面模型(RSM),并通过案例验证了模型的可靠性;Wang等[4-5]通过将序列二次规划法和响应面法相结合的方法,得出了薄板拉深工艺的最优成形条件;张骥超等[6-8]则在上述方法的基础上结合先进算法的应用,对多种情况下的多目标优化问题进行了探索。然而,这些研究几乎都是针对单工序的拉深成形,对级进模的研究也限于排样设计、压力中心确定[9-10],只有Li等[11-12]对级进模成形有限元分析方面进行了研究,而对级进模成形参数优化的研究鲜有报道。本文作者基于某阀门支架零件,采用多工步多工序建模的方法建立其级进模成形的全工序有限元模型;针对级进模成形可能出现的质量缺陷,给出一种级进模成形零件质量控制优化模型,并采用协同优化的响应面法对优化目标进行优化,得到优化目标与设计变量之间的二阶多项式响应模型及最佳成形参数组合。
1 级进模成形全工序有限元模拟
1.1 工艺分析及全工序建模
某空调阀门支架零件三维模型如图1所示。材料为电镀锌板SECC,厚度为1.45 mm,现有生产工艺为下料、拉深成形、切边冲孔、翻孔、折弯等单工序生产,该种生产方式因生产效率低、多次定位造成零件精度降低等问题不能满足目前的生产要求,因此,考虑采用级进模成形。工艺分析时采用6工位、中间载体、单排排样方式,排样图如图2(a)所示。
级进模成形包含多个工步,所以采用多工步多工序的方法建立全工序有限元模型。该方法根据不同工步的成形工序建立各个工步的凸凹模模型,凸模每动作1次,板料沿送料方向前进1个步距,实现板料在不同工步的连续成形。既保证板料在后续工步可以继承前一工步板料的变形、应力应变等信息,也能够分析相邻工步变形的相互影响。该模型使得模拟过程和实际级进模成形过程相吻合。使用该方法在Dynaform中建立的级进模成形全工序有限元模型如图2(b) 所示。

图1 零件三维模型
Fig. 1 3-D model of part
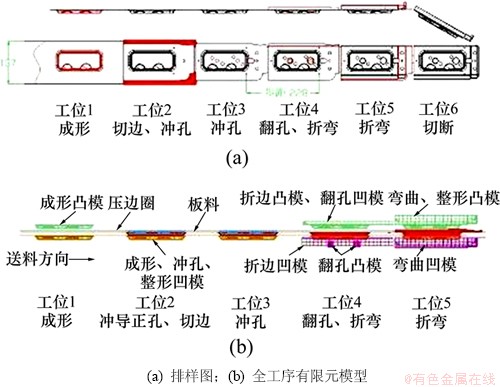
图2 排样图及全工序有限元模型
Fig. 2 Layout and finite element model of complete stamping process
1.2 级进模成形过程模拟
模拟时板料采用BT壳单元离散化处理,本构关系采用考虑各向异性的三参数Barlat材料模型,材料的部分性能参数如表1所示。模拟参数设置如下:虚拟冲压速度为2 m/s,凹模间隙为1.1t(t为板料厚度),摩擦因数为0.125,压边力为35 kN。第1工位数值模拟的成形极限图如图3所示。从图3可见:法兰边起皱比较明显,底部圆角也出现破裂的现象,说明工艺参数的选择不合理,为了得到满足质量要求的零件,需要对成形工艺参数进行优化。
表1 材料性能参数
Table 1 Performance parameters of material
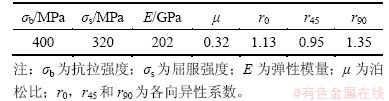
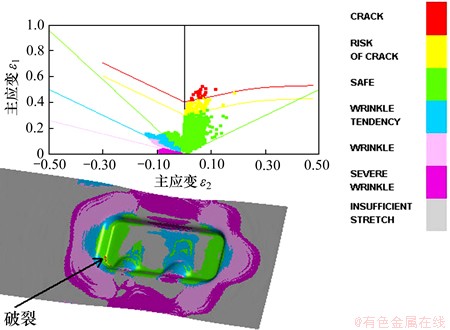
图3 第一工位成形极限图
Fig. 3 FLD of the first stamping process
2 零件质量控制优化模型的建立
2.1 优化目标和约束
本文将导正孔移动量作为成形精度的评价指标,将最大减薄率和最大增厚率分别作为破裂和起皱的评价指标。将最大减薄率、最大增厚率和导正孔移动量作为优化目标。为了保证零件的质量,既要避免起皱和破裂的发生,又要保证零件的成形精度,这是一个多目标的优化问题,且优化目标之间存在着耦合变量。单目标优化方法或是基于某一性能的多目标优化方法不能解决这一问题,因此,本文采用一种典型的多学科设计方法,实现优化目标之间的协同优化[13]。在数值模拟时,将3个评价指标量化为:导正孔移动量应小于0.1 mm,板料的最大变薄率应小于30%,最大增厚率应小于5%。
2.2 设计变量选取及优化模型建立
本文选取压边力x1、摩擦因数x2和凸凹模间隙x3作为设计变量,最小减薄率S1、最大增厚率S2及导正孔移动量y为目标函数,在约束函数条件下和参数取值范围内对目标寻优,优化模型为
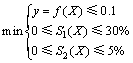 (1)
(1)
其中:X为x1,x2和x3的集合。
3 基于响应面法的成形参数优化
响应面法的基本思想是通过近似构造一个具有明确表达式的多项式来表达隐式功能函数[14-15],主要包括实验设计和响应面法优化2个部分。
3.1 实验设计及结果
本文借助专业的设计软件Design-Expert v8.0进行实验设计和分析。根据选取的设计变量,采用三因素五水平的中心复合设计来设计实验,共进行20次试验。中心复合试验设计因子水平如表2所示,实验安排及结果如表3所示。该零件设计变量取值范围为:20≤x1≤40 kN,0.08≤x2≤0.16,1.08t≤x3≤1.12t。
表2 因子水平的中心复合设计
Table 2 Central composite design of factor levels
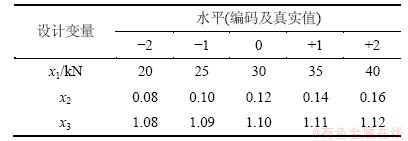
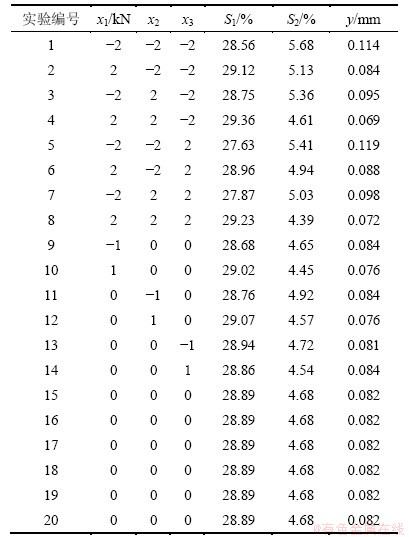
表3 实验安排及结果
Table 3 Experiment arrangement and results
3.2 模型构建及精度检验
响应面法能够通过简单的表达式对实际的板料冲压过程作逼近处理[4],本文采用二次多项式回归模 型[16]构建逼近响应值y的近似函数:
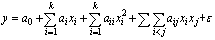 (2)
(2)
式中:xi为独立设计变量;n为设计变量个数;a0,ai,aii和aij为待求回归系数;ε为综合误差。
应用最小二乘法对表2的数据进行回归分析,得出响应值(S1,S2和y)与设计变量(x1,x2和x3)的响应函数如下:
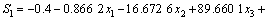
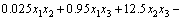
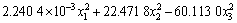 ; (3)
; (3)
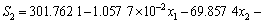
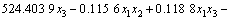
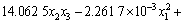
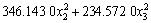 ; (4)
; (4)
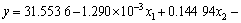
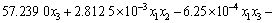
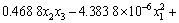
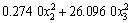 。 (5)
。 (5)
响应面模型的误差来源主要包含2个方面:一个是对空间样本点的拟合失真,另一个是因非试验样本点处的外推稳健性差而引起的“龙格效应”。因此,采用系数R2和修正系数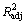 来验证模型对样本点的拟合精度,一般R2和
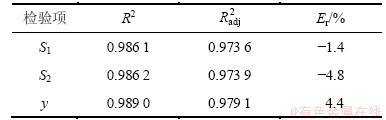
来验证模型对样本点的拟合精度,一般R2和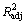 越接近1,模型拟合精度越高;用Er表示设计空间中随机生成10个测试点中的最大相对误差。式(3)~(5)中回归模型的误差评估如表4所示。由表4可见:Er在±5%以内,故所构建响应面模型精度较高,能够替代真实模型并用于后续的多目标寻优。
越接近1,模型拟合精度越高;用Er表示设计空间中随机生成10个测试点中的最大相对误差。式(3)~(5)中回归模型的误差评估如表4所示。由表4可见:Er在±5%以内,故所构建响应面模型精度较高,能够替代真实模型并用于后续的多目标寻优。
表4 回归模型误差评估
Table 4 Error evaluation for regression model
3.3 响应面结果分析
最大减薄率S1与成形参数压边力x1、摩擦因数x2、凸凹模间隙x3的响应面图如图4所示。由图4可见:最大减薄率随压边力和摩擦因数的增大而增大,随凸凹模间隙的增大而减小,且受压边力的影响最大。这是由于随着压边力和摩擦因数的增大,进料阻力也相应增大,使压边部分材料不易向变形区流动,从而使变形区材料变薄增大,而凸凹模间隙的增大则会减小进料阻力。当压边力为20~25 kN、摩擦因数为0.08~0.10和凸凹模间隙为1.11t~1.12t时可取得较小的减薄率。
最大增厚率S2与成形参数压边力x1、摩擦因数x2、凸凹模间隙x3的响应面图如图5所示。由图5可见:最大增厚率随压边力和凸凹模间隙的增大而减小,随摩擦因数的增大先减小后增大。这是由于压边力和凸凹模间隙的增大以及摩擦因数的适当增大有助于改善板料变形时进料阻力的均匀性,使材料流动均匀,从而减小了起皱的发生,即增厚率减小,而过大的摩擦因数则会降低材料流动的均匀性,从而造成起皱。当压边力为35~40 kN、摩擦因数为0.12~0.13和凸凹模间隙为1.11t~1.12t时可取得较小的增厚率。
导正孔移动量y与成形参数压边力x1、摩擦因数x2、凸凹模间隙x3的响应面图如图6所示。由图6可见:导正孔移动量随压边力和摩擦因数的增大而减小,随凸凹模间隙的增大而先减小后增大,而且导正孔移动量受凸凹模间隙与压边力以及凸凹模间隙与摩擦因数交互作用的影响。这是由于压边力和摩擦因数的增大,以及合适的凸凹模间隙值增大了压边部分的进料阻力,使压边部分材料不易变形,从而减小了导正孔移动量。当压边力为35~40 kN、摩擦因数为0.14~0.16和凸凹模间隙为1.09t~1.11t时可取得较小的导正孔移动量。
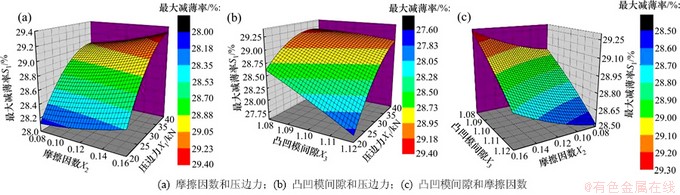
图4 成形参数对最大减薄率的影响
Fig. 4 Effect of forming parameters on maximum thinning ratio

图5 成形参数对最大增厚率的影响
Fig. 5 Effect of forming parameters on maximum thickening ratio
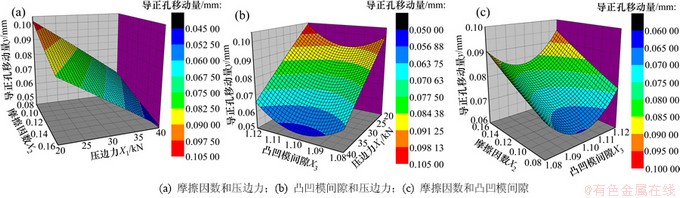
图6 成形参数对导正孔移动量的影响
Fig. 6 Effect of forming parameters on pilot hole movement
3.4 参数优化及有限元验证
在响应面模型拟合及实验结果分析的基础上,利用响应面优化软件对设计变量进行优化[17]。在设计变量的取值范围内,寻求优化目标的最小值,具体优化条件如表5所示。
经过软件分析,得到质量缺陷最小化的成形参数组合为:当x1=29.061,x2=0.1330 4,x3=1.108 9。在此成形参数下,S1=28.773 20,S2=4.614 62,y=0.082 311,优化目标均在要求范围内且取得较小值。因此,优化后的成形参数取值为:压边力x1=29 kN,摩擦因数x2=0.13,凸凹模间隙为x3=1.11t。采用优化后的成形参数进行模拟,第1工位成形极限图和厚度分布图如图7所示。对比图3与图7可知:优化后,成形时的破裂现象得到消除,材料的变形更加充分,起皱现象也得到改善。全工序成形极限图如图8所示。从图8可以看出:没有破裂缺陷,只有微量起皱。
表5 优化条件
Table 5 Optimum conditions
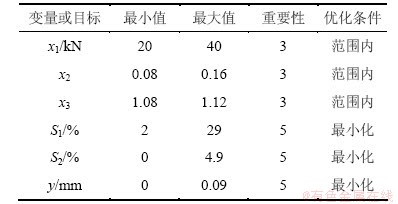
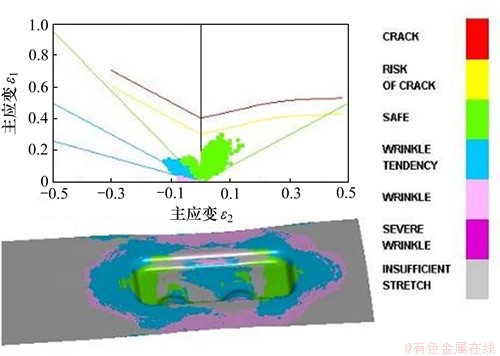
图7 第1工位成形极限图
Fig. 7 FLD of the first-stage stamping process
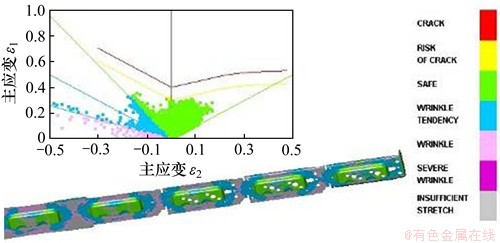
图8 全工序成形极限图
Fig. 8 FLD of complete stamping process
最终零件厚度分布如图9所示。经计算得零件的最大减薄率为28.89%,最大增厚率为4.93%,导正孔移动量为0.081 mm,均满足成形要求,模拟结果与优化结果基本一致,证明了优化模型的合理性及可行性。
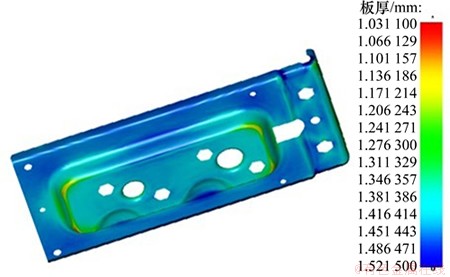
图9 优化后厚度分布图
Fig. 9 Thickness distribution after optimization
3.5 试模验证
将优化后的成形参数用于该阀门支架零件级进模成形的数值模拟和生产试制过程,试制带料图如图10所示。实际生产试制得到的带料与模拟结果相吻合,制件没有出现破裂,起皱缺陷也减少。采用检具对零件的成形质量进行测量,结果表明导正孔在成形过程中的移动量在0.07~0.09 mm之间,小于要求值0.10 mm,满足精度要求,实测厚度变化也满足使用要求。

图10 试制带料图
Fig. 10 Strip of trial product
4 结论
1) 建立了某阀门支架零件级进模成形的全工序有限元模型,使有限元模拟过程和实际的级进模生产过程相吻合。
2) 以最小减薄率、最大增厚率和导正孔移动量为优化目标,以压边力、摩擦因数和凸凹模间隙为设计变量,建立了阀门支架零件级进模成形的质量控制优化模型,使用响应面法得到了优化目标与设计变量之间的最优响应二次方模型,并对设计变量即成形参数进行了优化,得到质量缺陷最小化的成形参数组合,即压边力x1=29 kN,摩擦因数x2=0.13,凸凹模间隙x3=1.11t。
3) 运用优化后的工艺参数指导该零件的模具设计和生成试制过程,验证了本文采用模型和的合理性和可行性。该方法可以在模具设计阶段确保零件质量提高,并减少模具的开发周期,对级进模成形的模具设计和产品质量控制有重要的指导意义。
参考文献:
[1] 杨连发, 孙希延, 李泉永. 板料拉深成形数值模拟的关键技术[J]. 现代机械, 2002(3): 49-52.
YANG Lianfa, SUN Xiyan, LI Quanyong. Key technology in numerical simulation of sheet metal forming in drawing process[J]. Modern Machinery, 2002(3): 49-52.
[2] 孙光永, 李光耀, 陈涛, 等. 多目标粒子群优化算法在薄板冲压成形中的应用[J]. 机械工程学报, 2009, 45(5): 153-159.
SUN Guangyong, LI Guangyao, CHEN Tao, et al. Application of multi-objective particle swarm optimization in sheet metal forming[J]. Journal of Mechanical Engineering, 2009, 45(5): 153-159.
[3] Breitkopf P, Naceur H, Rassineux A, et al. Moving least squares response surface approximation: Formulation and metal forming applications[J]. Computers and Structures, 2005, 83(17/18 ): 1411-1428.
[4] Wang H, Li G Y, Zhong Z H. Optimization of sheet metal forming processes by adaptive response surface based on intelligent sampling method[J]. Journal of Materials Processing Technology, 2008, 197(1/2/3): 77-88.
[5] 孙永光, 李光耀, 郑刚, 等. 拉延成形多目标序列响应面法优化设计方法[J]. 力学学报, 2010, 42(2): 245-255.
SUN Guangyong, LI Guangyao, ZHENG Gang, et al. Muti-objective optimization for sheet metal forming of drawing with successive response surface method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(2): 245-255.
[6] 张骥超, 刘罡, 林忠钦, 等. 侧围外板冲压工艺稳健性优化设计[J]. 上海交通大学学报, 2012, 46(7): 1005-1010.
ZHANG Jichao, LIU Gang, LIN Zhongqin, et al. Robust optimization for an antobody outer panel stamping process[J]. Journal of Shanghai Jiaotong University, 2012, 46(7): 1005-1010.
[7] Zhang W F, Shivpuri R. Probabilistic. design of aluminum sheet drawing for reduce drisk of wrinkling and fracture[J]. Reliability Engineering and System Safety, 2009, 94(2): 152-161.
[8] LIU Wei, YANG Yuying. Multi-objective optimization of sheet metal forming process using Pareto-based genetic algorithm[J]. Journal of Materials Processing Technology, 2008, 208(1/2/3): 499-506.
[9] WEI Guangming, XIA Qinxiang, ZHANG Saijun, et al. Layout design for high strength steel automotive structural parts based on UG-PDW[C]// Proceedings of the 2nd International Conference on Mechanic Automation and Control Engineering. Inner Mongolia: IEEE, 2011: 5882-5885.
[10] JIA Zhixin, LI Honglin, ZHANG Xuechang, et al. Computer- aided structural design of punches and dies for progressive die based on functional component[J]. International Journal of Advanced Manufacturing Technology, 2011, 54(9/10/11/12): 837-852.
[11] Li J Y, Nee A Y C, Cheok B T. Integrated feature-based modelling and process planning of bending operations in progressive die design[J]. International Journal of Advanced Manufacturing Technology, 2002, 20(12): 883-895.
[12] Sheng Z Q, Taylor R, Strazzanti M. FEM analysis and design bulb shield progressive draw die[J]. Journal of Materials Processing Technology, 2007, 189(1/2/3): 58-64.
[13] 刘士士, 谷正气, 伍文广, 等. 基于响应面方法的车辆多目标协同优化[J]. 中南大学学报(自然科学版), 2012, 43(7): 2586-2592.
LIU Shishi, GU Zhengqi, WU Wenguang, et al. Multi-objective collaborative optimization of vehicle based on response surface methodology[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2586-2592.
[14] Nguyen X S, Sellier A, Duprat F, et al. Adaptive response surface method based on a double weighted regression technique[J]. Probabilistic Engineering Mechanics, 2009, 24(2): 135-143.
[15] ZHAO Weitao, QIU Zhiping. An efficient response surface method and its application to structural reliability and reliability- based optimization[J]. Finite Elements in Analysis and Design, 2013, 67: 34-42.
[16] 程洁青, 王玉超, 兰凤崇. 基于正交试验的汽车覆盖件冲压工艺参数优化[J]. 计算机集成制造系统, 2007, 13(12): 2433-2440.
CHEN Jiqing, WANG Yuchao, LAN Fengchong. Optimization for stamping process parameters of automotive body parts based on orthogonal experiments[J]. Computer Integrated Manufacturing Systems, 2007, 13(12): 2433-2440.
[17] 刘佳, 张宏, 石岩. 基于Design-Expert V7设计的不锈钢激光非熔透搭接焊工艺优化研究[J]. 机械工程学报, 2011, 47(16): 54-57.
LIU Jia, ZHANG Hong, SHI Yan. Technology optimizing research on laser non penetration lap welding of stainless steel based on design-expert V7[J]. Journal of Mechanical Engineering, 2011, 47(16): 54-57.
(编辑 杨幼平)
收稿日期:2014-02-17;修回日期:2014-04-19
基金项目(Foundation item):国家自然科学基金资助项目(51005258) (Project(51005258) supported by the National Natural Science Foundation of China)
通信作者:李军超,博士,副教授,从事板材成形过程数值模拟仿真与优化研究;E-mail: ljchust@163.com