基于BP神经网络的空间坐标视觉测量误差控制与补偿研究
李凯,袁峰,丁振良
(哈尔滨工业大学 测控技术与质量工程研究所,黑龙江 哈尔滨,150001)
摘要:基于在利用由2台经纬仪组成的空间三维坐标测量系统进行几何量测量的过程中,经纬仪的垂直角读数在特定位置会产生系统误差,并对精度带来不利影响,以空间三坐标测量系统作为研究对象,利用空间交汇原理建立了待测点坐标以及待测距离与经纬仪观测角的数学模型,分析了系统误差产生的原因。提出将系统误差作为非线性项,通过选取满足误差存在条件的数据训练网络令其逼近非线性函数,激励网络从而对系统误差进行有效控制和补偿。在仿真中根据精度指标不断优化BP神经网络的权值,获得了较好的神经网络参数配置。实验中补偿后测量结果与理论计算值较吻合,说明了这一方法的有效性。
关键词:空间坐标;神经网络;视觉测量;误差补偿
中图分类号:TH712 文献标志码:A 文章编号:1672-7207(2011)S1-0060-07
Vision measurement error control and compensation of spatial coordinates based on BP neural network
LI Kai, YUAN Feng, DING Zhen-liang
(Institute of Measurement & Control and Quality Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract: Based on the fact that during the geometric variables measurement course of spatial three-dimension coordinates by bino-theodolites, system errors of vertical observing angles’ reading occur at certain position by experiment data, the result of which leads to bad effects to precision, objected to spatial coordinates measurement system, the mathematic model of point coordinate and distance to be measured was established, and the cause of system error by means of space rendezvous and docking technology was analyzed. The idea was proposed of regarding system error as nonlinear component, training neural network’s (NN) by samples met the condition of system error existence to approach nonlinear function, and exciting NN to efficiently control and compensate system errors. In simulation, the weights of NN were optimized according to the precision performance index, and better parameters’ configurations were obtained. In experiment, consistence degree of compensated results and theoretical results validates the effectiveness of this method.
Key words: spatial coordinates; neural network; vision measurement; error compensation
经纬仪作为一种较高精度的测角设备被广泛应用于几何量测量和外部设备的标定过程中。无论是电子式还是光学式经纬仪,都能够获得基于经纬仪自身坐标系的水平观测角和垂直观测角读数。根据角度读数和空间几何关系可以获得空间坐标和距离的信息,完成对几何量的间接测量,于是,由2台经纬仪便可以构成空间三坐标测量系统[1]。在测量单点坐标时,经纬仪自身坐标系通过水平轴线和垂直轴线的配准统一到整个三维测量系统的坐标系中,根据空间前方交汇原理获得全局标定点的空间三维物体坐标[2],如图1所示。图1中,待测坐标点为P点,当经纬仪A和B同时瞄准空间点P时,测量数据为目标点的水平观测角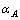 ,
,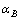 和垂直观测角
和垂直观测角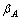 和
和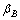 ,若已知2台经纬仪的水平距离b和高度差h,则根据几何关系可求出P点相对于空间测量坐标系的三维坐标。
,若已知2台经纬仪的水平距离b和高度差h,则根据几何关系可求出P点相对于空间测量坐标系的三维坐标。
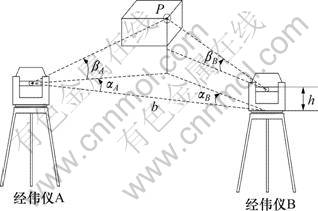
图1 双经纬仪三维空间测量系统
Fig.1 Spatial three-dimension measurement system by bino-theodolites
通常经纬仪的水平观测角范围为0°~180°,垂直观测角范围为0°~90°。在测量过程中,首先要定义零点,而后测量待测坐标点,实际记录读数是待测坐标点与零点的差值。零点位置要求双经纬仪的水平观测轴线重合,垂直观测轴线与水平观测轴线严格正交,此时垂直观测角的读数为90°,由于待测目标和经纬仪观测轴线的相对位置不同,很可能会出现垂直观测角读数穿越90°的情况。在90°附近,实验表明实际计算距离与理论上的被测距离会出现误差。这个误差是一个具有非线性特征的系统误差,不仅与垂直观测角的数值有关,而且与2台经纬仪之间的距离相关[3],同时,还会给空间点坐标的计算带来不利影响。为了在不同垂直观测角和不同经纬仪间距的情况下都可以有效地补偿这个系统误差,本文将经纬仪间距定为一个常量,基于空间坐标反求法建立了观测角与被测距离的测量方程,提出了构建反映观测角与被测距离之间非线性映射关系的BP型神经网络,以带有系统误差的实验数据训练网络,通过优化权值获得合适的参数配置并以新的测量数据激励网络获得系统误差的补偿项从而去除系统误差的方法。在具体研究中,首先利用标准量块根据坐标反求法获得了2台经纬仪之间的精确距离;其次构建了带有非线性项的测量系统数学模型,建立了观测角—被测距离的非线性映射关系;而后利用含有系统误差的观测数据训练BP神经网络,以精度准则优化了网络权值,获得了较好的权值参数配置;最后利用新测量的数据激励BP神经网络,获得补偿项,并进行了精度校验。实验结果显示补偿后的被测距离与理论计算的被测距离偏差较小,精度分析的结果说明此方法能有效地降低系统误差对测量结果的影响。
1 理论分析
图1中,进行了作如下的简化处理:
(1) 将经纬仪的观测镜头等效为1个坐标点,即经纬仪在三维测量坐标系下只等效为1个坐标点。其水平观测轴线和垂直观测轴线也相交在这个点上。
(2) 忽略2台经纬仪之间垂直高度差h的影响。由于大地基准面,三脚架和经纬仪都是相同的,即使出现高度差仍然可以通过高度调整使经纬仪等高,因此,h的影响可以忽略不计。
1.1 双经纬仪测量坐标系
在空间三维坐标系中,令经纬仪分别位于O点和B点,设OB的间距为L。以OB为X轴,根据右手定则建立空间三维笛卡尔坐标系,如图2所示。A1和A2为2个待测的空间坐标点,其在O-XYZ坐标系下的坐标分别为(x1, y1, z1)和(x2, y2, z2)[4]。设A1和A2 2点的距离为L12,A1和A2点在O-XY平面内的投影位置是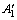 点和
点和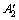 点,其三维坐标为(
点,其三维坐标为(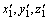 ) 和(
) 和(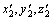 )。2台经纬仪记录的水平观测角分别为
)。2台经纬仪记录的水平观测角分别为 和
和 以及
以及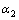 和
和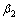 ,记录的垂直观测角为
,记录的垂直观测角为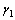 ,
,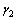 和
和 ,
,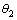 。根据三角公式可以计算出O和B 2点的间距L以及A1和A2 2点的空间距离L12之间的关系,还有A1和A2点在O-XYZ三维空间坐标系下的三维坐标(x1, y1, z1)和(x2, y2, z2)。
。根据三角公式可以计算出O和B 2点的间距L以及A1和A2 2点的空间距离L12之间的关系,还有A1和A2点在O-XYZ三维空间坐标系下的三维坐标(x1, y1, z1)和(x2, y2, z2)。
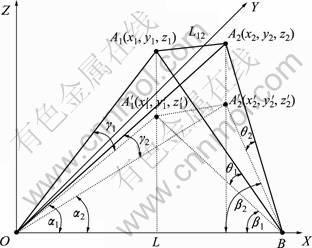
图2 双经纬仪空间测量坐标系
Fig.2 Spatial measurement coordinates of bino-theodolites
1.2 测量系统的数学模型
由图2和三角关系中的正弦定理,得:

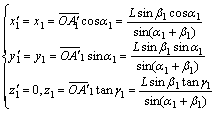 (1)
(1)
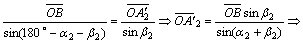
 (2)
(2)
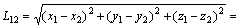
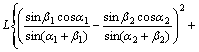
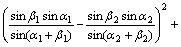
 (3)
(3)
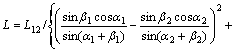
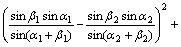
 (4)
(4)
式(3)和式(4)说明经纬仪间距和被测距离可以相互反求。
1.3 测量结果的系统误差
由式(1)~(4)可知,当已知2台经纬仪的观测角后,L和L12可以相互转化,而且它们都是关于观测角的非线性函数。由式(3)得到:
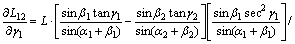
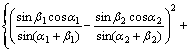
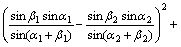
 (5)
(5)
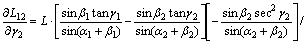
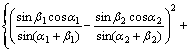
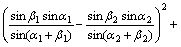
 (6)
(6)
式(5)和式(6)可以进一步简化为:
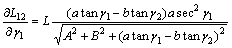 (7)
(7)
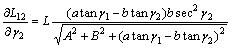 (8)
(8)
式中:
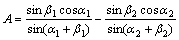 ;
;
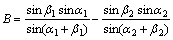 ;
;
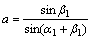 ;
;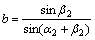
A项和B项均与垂直观测角无关。由于三角函数关系,垂直观测角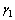 和
和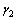 在90°附近的
在90°附近的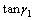 和
和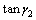 以及
以及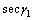 和
和 都趋近于无穷大,即式(7)和式(8)出现
都趋近于无穷大,即式(7)和式(8)出现
了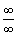 的情况。这说明在90°附近垂直观测角所引起的
的情况。这说明在90°附近垂直观测角所引起的
距离误差系数较大,导致距离误差较大,这就是产生系统误差的原因。而且只有当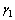 或
或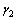 在90°附近时系统误差才存在,若
在90°附近时系统误差才存在,若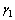 和
和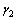 均远远小于90°或远远大于90°,则系统误差不存在。式(3)可以写成:
均远远小于90°或远远大于90°,则系统误差不存在。式(3)可以写成:
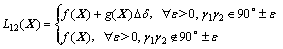 (9)
(9)
式中: ;
;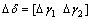 。
。
2 非线性项的神经网络逼近
式(9)所示的函数关系可以看作从X到L12(X)的某种非线性映射,且当X向量中的某些分量处在特定邻域内,将会产生一个系统误差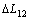 。若要补偿这个系统误差,则必须保证误差的存在条件。
。若要补偿这个系统误差,则必须保证误差的存在条件。
BP神经网络从理论上来说具有以任意精度逼近任意非线性函数的能力,而且相比于传统的硬计算方法,它能够根据训练样本的特性,通过适时地改变网络权值,在有监督的学习下,满足最小二乘意义下指标函数最小。在仿真实验中,利用满足领域条件的样本训练网络,以精度指标来优化输入层与隐含层的连接权值。在实验中进行精度分析和误差补偿。
2.1 构造训练样本
在实验中,利用二维目标模拟器构造测量坐标点,在实际测量过程中选取了目标模拟器XY平面上的20个坐标点,如图3所示。图3中,A5为坐标零点,每相邻2点之间的理论间距为480 mm。

图3 目标模拟器的测试点分布
Fig.3 Test dots’ distribution of object simulator
(1) 采用80 mm标准量块反求两经纬仪之间的间距(量块是长度计量的标准,就是把量块的长度当成一个基准即确定的距离,利用空间几何关系反求2点的坐标。这里利用的是二等量块,根据JJ G146—94的规定,其标准不确定度为U=(0.05+0.5L) μm。其中:L为量块的标称长度(m)。当置信概率P=0.99时,置信因子k=2.58,满足精度指标要求)。在式(4)中,令L12=80 mm,并记录此时获得的观测角: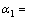 53°22′25″,
53°22′25″, 42°3′24″,
42°3′24″,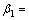 37°25′12″,
37°25′12″,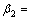 46°31′41″,
46°31′41″,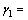 13°17′1″,
13°17′1″,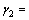 11°9′16″,
11°9′16″,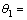 9°56′3″,
9°56′3″,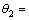 11°50′50″。精确得到2台经纬仪之间间距L为 4.592 12 m。
11°50′50″。精确得到2台经纬仪之间间距L为 4.592 12 m。
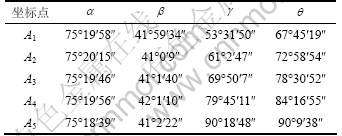
(2) 利用双经纬仪进行测量,获得了20组观测角数值。经过分析,在测量A5点和A4点时,垂直观测角穿越了90°,因此,以A1~A5这5个点的测量数据作为训练样本,样本数据如表1所示。
表1 测量数据
Table 1 Test data
2台经纬仪的初始相对位置为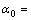 0°0′0″,
0°0′0″,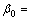 74°20′7″,
74°20′7″,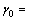 90°0′0″,
90°0′0″,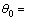 90°0′7″。表1中,相对应的测量角与初始位置对应的测量角之差即是式(3)和(4)的
90°0′7″。表1中,相对应的测量角与初始位置对应的测量角之差即是式(3)和(4)的 ,
,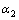 ,
, ,
,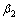 ,
,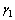 ,
,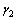 ,
, 和
和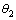 。整个神经网络的训练样本的输入数据为
。整个神经网络的训练样本的输入数据为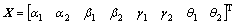 ,输出数据为实际的测量点间距L54,L53,L52和L51。
,输出数据为实际的测量点间距L54,L53,L52和L51。
2.2 训练网络优化权值
神经网络选择具有1个输入层、1个隐含层和1个输出层的3层网络。其中输入层的神经元数目为8,中间层的神经元数目为2,输出层的神经元数目为1。激励函数采用tansig型函数,训练算法为Levenberg- Marquardt。满足不同训练误差要求的训练误差曲线和权值关系曲线如图4~7所示。从图4~7可见:
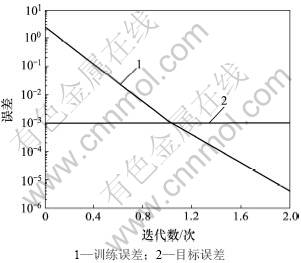
图4 目标精度为10-3的误差曲线
Fig.4 Error curves when target precision is 10-3
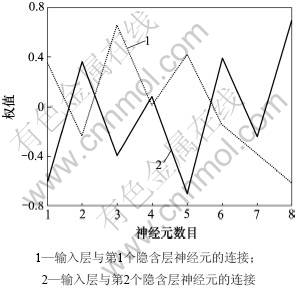
图5 目标精度为10-3的权值变化
Fig.5 Weights’ variation when target precision is 10-3
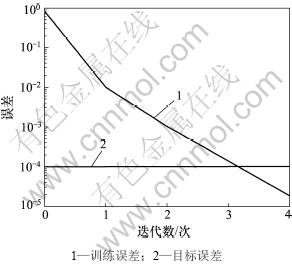
图6 目标精度为10-4误差曲线
Fig.6 Error curves when target precision is 10-4
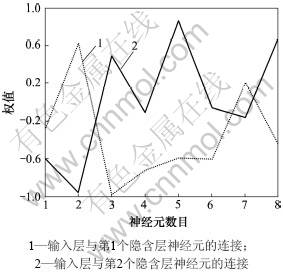
图7 目标精度为10-4的权值变化
Fig.7 Weights’ variation when target precision is 10-4
(1) 在训练次数均在100以内的情况下,误差要求越高,训练次数越高。
(2) 精度要求越高,权值的变化范围越大,例如:当精度要求为0.001时,权值的变化范围为[-0.8, 0.8];当精度要求为0.000 1时,权值的变化范围为[-1,1]。但算法能保证收敛。
3 实验结果验证
为了验证神经网络的逼近效果,选取图3中A6~A10这5个点激励网络,并利用以训练好的神经网络计算补偿项。当导轨垂直运动时,得到如下的相对位置计算结果:A6坐标点位置为(652.730 3, 14.077 1, 2 489.978 0) mm,经过神经网络计算后得到的补偿项为28.205 7 mm,得到表2所示的结果。
表2 坐标和距离标定结果
Table 2 Calibration results of coordinates and distances
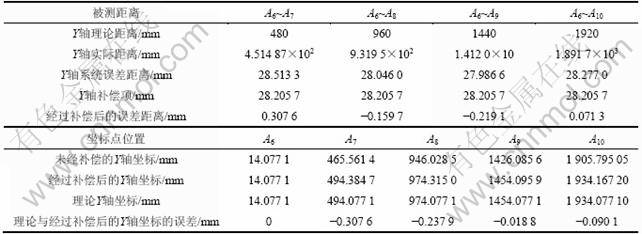
表2说明:神经网络的补偿结果能够有效地降低垂直角的系统误差,经过补偿后的距离误差出现正负现象说明补偿的效果较好。而修正测量点的坐标仍然全部为负,说明网络训练的结果与训练样本仍然有一定的关系,但是,其误差值已经降低了2个数量级,说明这种方法可以降低系统误差的影响。
实验中同时用这种方法测量并且补偿了极端情况的坐标点数值,整个二维模拟器测量区域顶部和底部测量点坐标如图8和图9所示。
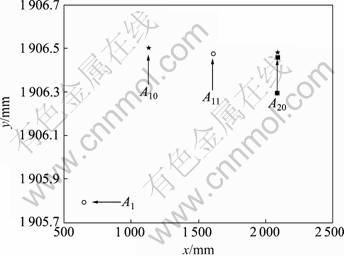
图8 顶部测量点坐标
Fig.8 Test dot coordinates at top area
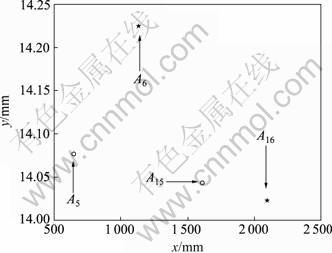
图9 底部测量点坐标
Fig.9 Test dot coordinates at bottom area
图8和图9说明:采用神经网络进行误差补偿之后,修正的待测点的坐标无论是在测量区域的顶部还是在测量区域的底部,其数值变化的范围较小,与理论计算值的偏差有所降低。
4 精度分析
根据式(1)和式(2)得:
 (10)
(10)
由式(10)得:
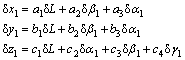 (11)
(11)
XY坐标的标准不确定度为:
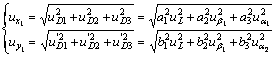 (12)
(12)
根据误差的等作用原则,规定L, 和
和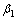 的标准不确定度分量应该是总的标准不确定度分量的平方根均分,已知总的标准不确定度uD=3 mm,则有:
的标准不确定度分量应该是总的标准不确定度分量的平方根均分,已知总的标准不确定度uD=3 mm,则有:
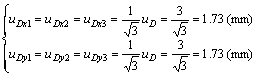 (13)
(13)
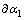 和
和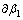 等误差是由于经纬仪读数造成的误差,由于经纬仪精度为2″,实验的视距为2 330 mm,因此,经纬仪读数引起的位移误差为[5-10]:
等误差是由于经纬仪读数造成的误差,由于经纬仪精度为2″,实验的视距为2 330 mm,因此,经纬仪读数引起的位移误差为[5-10]:
 <<
<<  (14)
(14)
有理由认为以上3个误差项中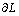 较大,又由于
较大,又由于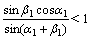 ,因此,可以认为
,因此,可以认为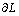 <1.73 mm是满足精度要求的最低条件。经纬仪的间距L是通过对标准量块的坐标反求法求出的,而且从表2可看出经过补偿后的L12的误差均小于1.73 mm,因此,可以说明采用这种方法能够保证控制精度为3 mm的要求。
<1.73 mm是满足精度要求的最低条件。经纬仪的间距L是通过对标准量块的坐标反求法求出的,而且从表2可看出经过补偿后的L12的误差均小于1.73 mm,因此,可以说明采用这种方法能够保证控制精度为3 mm的要求。
5 结论
(1) 通过分析双经纬仪空间三维测量系统垂直观测角在90°附近的系统误差产生原因,提出利用神经网络对这一非线性项进行逼近,通过选取满足系统误差存在条件的样本训练网络从而获得补偿量并修正坐标数据的方法。
(2) 在实验中,采用离线训练,通过网络权值的优化获得较好的网络参数,并利用不同的样本数据进行验证和精度分析,待测距离和待测坐标的系统误差都有明显的降低说明这种方法具有一定的功效。此项工作仅是针对Y轴进行系统误差补偿,XYZ都出现系统误差,它们之间能够完全解耦,那么仍然可以利用这一方法进行补偿。
(3) 在训练样本中如何进一步确定误差存在条件的邻域范围,逼近神经网络结构的因素和学习算法的选取与收敛性对这一非线性逼近的结果是否有影响有待进一步研究。
参考文献:
[1] 周富强, 张广军, 江洁, 等. 现场双经纬仪三维坐标测量系统[J]. 机械工程学报, 2004, 40(1): 165-169.
ZHOU Fu-qiang, ZHANG Guang-jun, JIANG Jie, et al. Three-dimensional coordinate measuring system with bino- theodolites on site[J]. Chinese Journal of Mechanical Engineering, 2004, 40(1): 165-169.
[2] 张滋黎, 邾继贵, 耿娜, 等. 双经纬仪三维坐标测量系统设计[J]. 传感技术学报, 2010, 23(5): 660-664.
ZHANG Zi-li, ZHU Ji-gui, GENG Na, et al. The design of double-theodolite 3D coordinate measurement system[J]. Chinese Journal of Sensors and Actuators, 2010, 23(5): 660-664.
[3] ZHOU Hu, ZHU Ji-gui, YE Sheng-hua, et al. Resolution improvement of the electronic theodolite in automatic guided laser theodolite system by subdivided locating method of image[C]//Proceedings of SPIE the International Society for Optical Engineering. Beijing: SPIE, 2008: 716001-716009.
[4] LIANG Wei, GUO Jin. The research on servo control technology of O-E theodolite based on angular acceleration sensor[C]//2010 International Conference on Computer, Mechatronics, Control and Electric Engineering (CMCE), 2010: 629-632.
[5] 刘延斌, 金光, 何惠阳. 目标模拟器的控制误差研究[J]. 系统仿真学报, 2004, 16(4): 820-824.
LIU Yan-bin, JIN Guang, HE Hui-yang. Research on control error of an target simulator[J]. Acta Simulata Systematica Sinica, 2004, 16(4): 820-824.
[6] Luna C A, Mazo M, Lazaro J L, et al. Reduction of vibration- induced errors in 3D measurement system with vision and structured light[C]//IEEE ISIE. 2005: 1291-1296.
[7] Nagatomo S, Hayashi J, Hata S. Proposal of calibration error-tolerant 3D measurement method using stereo vision for robot vision[C]//Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation. Changchun, China, 2009: 3263-3268.
[8] Holger Handel. Compensation of thermal error in vision based measurement systems using a system identification approach[C]//ICSP2008 Proceedings. Leipzig, Germany, 2008: 1329-1333.
[9] HUANG Jian, Kosaka S, Imamura Y, et al. Measurement of distance error in reaching movement of the human hand without using vision[C]//Proceedings of the 29th Annual International Conference of the IEEE EMBS. Lyon, France, 2007: 4866-4869.
[10] 魏超, 李明荣, 张增太. 双经纬仪测量系统在测量精密骨架中的应用[J]. 电子机械工程, 2007, 23(2): 1-5.
WEI Chao, LI Ming-rong, ZHANG Zeng-tai. Application of a pair of theodolites in the height dimensional precision structural framework measurement[J]. Electro-Mechanical Engineering, 2007, 23(2): 1-5.
(编辑 陈灿华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(51075195);中央高校基本科研业务费专项资金资助项目(HIT.NSRIF.2010100)
通信作者:李凯(1979-),男,黑龙江哈尔滨人,讲师,从事计算机视觉测量、数字图像处理、运动控制研究;电话:13936591434;E-mail: likaihit@gmail.com