考虑齿向修形与安装误差的圆柱齿轮接触分析

唐进元，陈兴明，罗才旺

(中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083)

摘要：提出一种齿向修形的等半径圆弧鼓形齿面新结构，根据齿向修形原理推导出等半径圆弧鼓形齿面方程，构建含安装误差的主动轮鼓形齿与未修形从动轮渐开线齿的接触分析(TCA)模型，给出TCA算法和算例。TCA计算结果表明：齿轮轴线的中心距误差对这种鼓形齿传动的接触轨迹影响很小，鼓形修形量、鼓形中心与齿宽中点的偏差及齿轮轴线的平行度误差都将对齿轮接触轨迹产生较大影响；通过调整修形参数和安装误差可以精确的预控接触轨迹的位置，这对高性能齿轮传动设计制造有较大参考价值。

关键词：直齿圆柱齿轮；齿面接触分析(TCA)；齿向修形；安装误差；等半径圆弧鼓形齿

中图分类号：TH132.41            文献标志码：A         文章编号：1672-7207(2012)05-1703-07

Contact analysis of spur gears based on longitudinal modification and alignment errors

TANG Jin-yuan, CHEN Xing-ming, LUO Cai-wang

(State Key Laboratory for High Performance Complex Manufacturing,

School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract: A new kind of longitudinal modified equal radius arc crown gear tooth surface was proposed, according to the principle of longitudinal modification derived equal radius arc crown gear tooth surface equation, the tooth contact analysis (TCA) model of drum-shaped driving pinion and no modification driven gear with the alignment errors was built, and the TCA algorithm and examples were given. The numerical results of TCA show that error of the gear axis from the center of drum-shaped tooth has little effect on the contact path, while the amount of drum-shaped modification, the deviation errors drum-shaped center to the tooth width midpoint and the gear axis parallel error have a significant impact on contact path. The location of contact path can be accurately pre-controlled by adjusting the modification parameters and alignment errors, which will have a larger reference value to the design and manufacture of high-performance gear drives.

Key words: spur gear; tooth contact analysis (TCA); longitudinal modification; alignment error; equal radius arc crown gear

渐开线圆柱齿轮传动因其结构紧凑、便于制造和维护以及传动平稳等特点而被广泛应用，在齿轮传动中，由于安装误差和弹性变形的影响，使齿面发生边缘接触和应力集中，易造成齿面失效^[1]。齿向修形能降低对安装误差的敏感度，减少齿顶啮合冲击及噪声，改善齿轮轴向弯曲和扭转变形而造成的载荷集中，使载荷沿齿向分布均匀，提高齿轮啮合性能^[2-6]。Alfonso等^[7-8]研究了用齿条加工齿向修形斜齿轮的TCA分析；Litvin等^[9-12]研究了用砂轮加工齿向修形斜齿轮的TCA分析和接触应力分析。国内相关研究主要集中在齿向修形量的确定及其实验结果分析^{[1, 13]}，针对齿向修形齿轮接触特性的TCA分析文献还极为少见。本文作者从齿面接触分析(TCA)的角度研究齿向修形，为节约制造成本，研究主动轮小轮齿向修形，从动轮大轮不修形的传动形式。首先根据齿轮鼓形修形原理，结合渐开线方程推导了鼓形齿轮的齿面方程；然后构建存在安装误差的齿面接触分析模型，对接触点进行数值仿真分析，实现了鼓形修形齿轮的接触轨迹的可视化，研究了鼓形修形参数及不同安装误差项对接触轨迹的影响规律。

1  齿面方程推导

1.1  齿向鼓形修形小轮齿面方程

本文提出一种等半径圆弧鼓形齿新齿面结构，如图1所示，图1中虚线表示修形后的齿廓、实线表示修形前的齿廓，修形齿面由原来的渐开线上的任意点p沿着渐开线的法线方向齿面内部偏移l_p。图2所示为修形小轮齿顶面投影图。坐标系统S₁(x₁, y₁, z₁)固定在小轮上，y₁与相邻两齿槽的对称线重合，z₁与齿轮轴线重合，原点O₁取在齿宽的中点位置，?l为最大鼓形量，R_g为鼓形半径，b为齿宽，?w为鼓形中点与齿宽中间位置的偏差，当?w不为零时，齿面将是非对称的鼓形，对于齿廓上的一点p，设其鼓形量为l_z沿齿向的坐标值z_p，从图2所示关系可以得到：

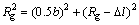         (1)

        (2)

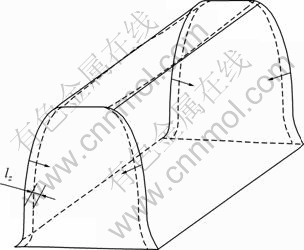
图1  小轮鼓形修形

Fig.1  Drum modification of pinion

图2  修形小轮齿顶投影

Fig.2  Tip projection of modified pinion

联立式(1)和(2)得到齿廓上点p的鼓形量l_p的表达式，当齿宽b，最大鼓形量?l和偏差?w给定后，l_p只是轴向参数u₁的函数。

图3所示为修形齿轮的齿向投影。图中，η_η为修形前的渐开线齿廓；α_α 为修形后齿廓。η_η在S₁中可以表示为：

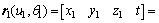
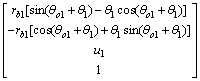     (3)

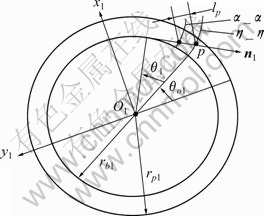
图3  小轮齿向投影

Fig.3  Tooth projection of modified pinion

当η_η上任意点p沿着n₁负方向往α_α偏移l_p时，偏移量在x₁和y₁方向上满足下列关系：

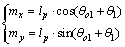             (4)

由于是齿向修形，所以齿宽方向的坐标值z ₁与u₁是一致，联立式(3)和(4)得到修形后的齿面方程为：

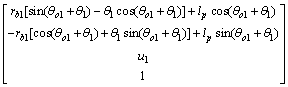(5)

小轮齿面单位法矢为：

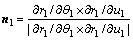           (6)

其中：r_b1为基圆半径；r_b1为分度圆半径；u₁为沿小轮齿向方向的齿面参数；θ₁为渐开线参数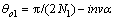；为齿槽参数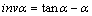；为渐开线函数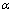；为压力角。

1.2  大轮齿面方程

如图4所示，坐标系S₂(x₂, y₂, z₂)固定在大轮上，y₂与相邻两齿槽的对称线重合，z₂轴与大轮轴线重合且垂直齿面向外，由于大轮齿面是不修形的渐开线，容易得到其齿面方程：

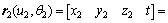
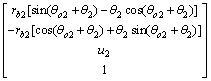     (7)

图4  大轮齿向投影

Fig.4  Tooth projection of modified gear

单位法矢为：

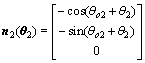         (8)

2  含安装误差的轮齿接触分析(TCA)模型与方法

2.1  轮齿接触分析坐标系的确定

经过如下步骤建立鼓形小轮与标准大轮存在安装误差情况下的接触坐标系：

(1) 使用鼓形齿轮轴线与标准直齿轮轴线建立轴线平面；垂直平面为过鼓形齿轮轴线并垂直于轴线平面的平面。

(2) 以鼓形齿轮轴线中点为原点，鼓形齿轮轴线为z轴，轴线平面为坐标系xz平面，建立绝对坐标系σ_f (O_f , x_f, y_f, z_f)。

(3) 平移绝对坐标系σ_f的原点O_f到标准直齿轮轴线中点得到只有中心距偏差而无平行度偏差的标准直齿轮位置参考坐标系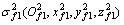；再将坐标系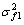进行偏转(偏转角度为轴平面内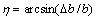，垂直平面内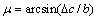)得到含有中心距与平行度偏差的标准直齿轮转动参考坐标系。

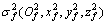由上述建立齿轮接触坐标系的过程可知接触分析时鼓形齿轮固联坐标系S₁的z轴与绝对坐标系的z轴重合，标准直齿轮固联坐标系S ₂的z轴与坐标系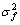的z轴重合，如图5所示。

结合前文的齿面方程与确立的接触坐标系系统，可以写出在绝对坐标系下，参与啮合两齿轮的齿面方程：鼓形小轮齿面方程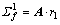和标准大轮轮齿面方程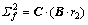。r₁和r₂分别为小轮和大轮在各自固联坐标系中的齿面方程；A和B分别为鼓形齿轮、标准直齿轮固联坐标系S₁和S₂到坐标系和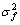的坐标转换矩阵；C为标准直齿轮的转动参考坐标系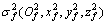到绝对坐标系的转换矩阵。

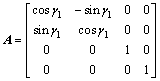
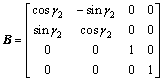
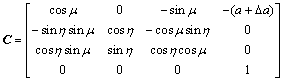
其中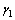：和分别为小轮和大轮的转角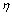；和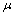分别为轴平面内及垂直平面内两齿轮轴线的平行度误差；为中心距安装误差。

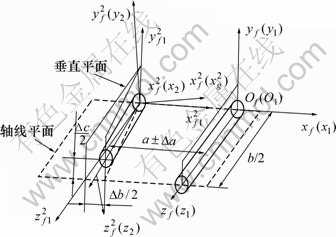
图5  含安装误差的接触分析坐标系

Fig.5  Contact analysis coordinates with alignment errors

2.2  接触轨迹求解

根据齿轮啮合原理^[14]，2个齿面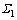和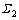要能够保持连续的切触一定要满足它们的位置矢量和单位法矢时刻相等：

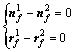               (9)

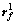式中：和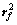分别为小轮和大轮在绝对坐标系中的齿面方程。在直角坐标系中其理论上等效于6个表达式，但是只有5个独立方程^[15]，含有θ₁，θ₂，u₁，u₂，γ₁和γ₂ 6个未知数。给定一系列小轮的转角γ₁，求解含有5个未知数的非线性方程组^[16]，可以得到每一个接触点的其他5个参数，由u₁和θ₁可以确定小轮上接触点位置，u₂和θ₂可以确定大轮上接触点位置，将求解得到的接触点依次连接得到接触轨迹。

3  算例及分析

根据上述分析，采用一对实际齿轮来研究安装误差及鼓形参数对鼓形修形齿轮接触轨迹的影响规律。实例计算中使用的齿轮模数m=4，小轮齿数z ₁=17，齿宽b₁=42 mm，大轮齿数z₂=33，齿宽b₂=42 mm，压力角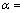25°。

3.1  安装误差对鼓形齿轮接触轨迹的影响

取?l=0.05 mm、?w=0 mm，考虑到在工程实际中每种安装误差都可能存在，因此在研究不同安装误差项对鼓形齿接触轨迹的影响时只变动所要研究的安装误差，另外两项安装误差为固定的非零值。具体的各项安装误差取值如表1所示。工况A为没有安装误差的理想安装，作为其他工况的参照；B，C和D 3种工况用来研究轴平面内轴线平行度误差对鼓形齿接触轨迹的影响；E，F和G 3种工况用来研究垂直平面内轴线平行度误差对鼓形齿接触轨迹的影响；H，I和J  3种工况用来研究中心距误差对鼓形齿接触轨迹的影响，求得的接触轨迹如图6~8所示。

表1  安装误差取值表

Table 1  Table of alignment errors values

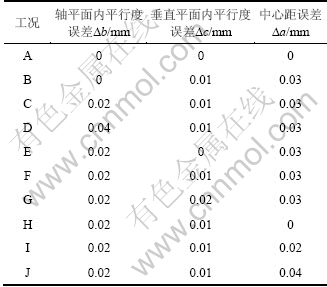
图6  轴平面内平行度对接触轨迹的影响

Fig.6  Effect of axial plane parallel to contact path

图7  垂直平面内平行度对接触轨迹的影响

Fig.7  Effect of vertical plane parallel to contact path

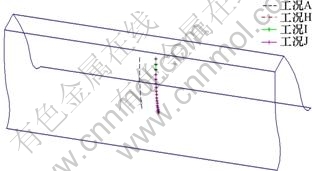
图8  中心距偏差对鼓形齿轮接触轨迹的影响

Fig.8  Effect of center distance deviation to contact path of drum gear

由图6可见：无安装误差时齿轮的接触轨迹位于轮齿齿宽中间位置，随着轴平面平行度误差的增大接触轨迹逐渐偏离了齿宽中间位置。可见轴平面内轴线平行度偏差的增加会使齿轮的接触轨迹偏离齿宽中间位置的距离增大；但是接触轨迹偏离增加的幅度有减少的趋势；说明随着轴平面内轴线平行度偏差的增大，接触轨迹对其敏感度在降低。

由图7可知：随着垂直平面内轴线平行度偏差的增大，接触轨迹偏离齿宽中点距离也相应增大，并且发现各个接触轨迹的间距基本不变，可见接触轨迹对垂直平面内轴线平行度偏差的敏感度基本上没有   变化。

由图8可见：含安装的误差的鼓形修形齿轮接触轨迹基本重合在一起，说明中心距误差的变化对接触轨迹位置基本没有影响，这一点与未修形的标准圆柱齿轮是一致的。

采用无安装误差、轴平面内平行度误0.02 mm和垂直平面内轴线平行度偏差0.01 mm 3种工况进行对比，如图9所示。由图9观察发现：垂直平面内平行度轴线偏差0.01 mm工况使接触轨迹偏离齿宽中心稍远。说明垂直平面内平行度偏差对接触轨迹的影响比轴平面内轴线平行度偏差对接触轨迹的影响要大得多，就计算的结果来看应该在两倍以上。

图9  轴平面内轴线平行度偏差与垂直平面内轴线平行度偏差对鼓形齿轮接触轨迹影响的对比

Fig.9  Contrast of effects of axial plane parallel and vertical plane parallel to contact path

3.2  鼓形参数对鼓形齿接触轨迹的影响

取安装误差?a=0.02 mm，?b=0.02 mm，?c=0.01 mm，最大鼓形量?l及?w的取值如表2所示。工况K，L和M研究最大鼓形量对鼓形齿接触轨迹的影响，工况N，P和Q研究鼓形中心与轮齿中心偏差?w对鼓形齿接触轨迹的影响。

表2  鼓形参数取值表

Table 2  Table of drum parameters values

图10所示为鼓形量对鼓形齿轮接触轨迹的影响。由图10可见：随着鼓形量的增大接触轨迹逐步向轮齿中间位置靠近。但是鼓形量取0 mm与取0.04 mm时两接触轨迹之间间距要大于取0.04 mm与取0.08 mm时两接触轨迹之间间距，说明随着最大鼓形量的增大鼓形齿接触轨迹对其的敏感度在降低，所以只调节鼓形量的大小对控制鼓形齿接触轨迹的作用是有限的。

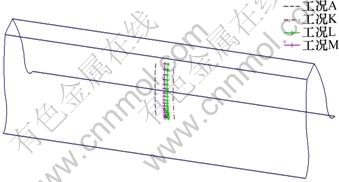
图10  鼓形量对鼓形齿轮接触轨迹的影响

Fig.10  Effect of drum amount to drum gear contact path

图11所示为鼓形中点位置对鼓形齿轮接触轨迹的影响。由图11可见：鼓形齿轮的接触轨迹位置随着?w的变化在齿宽方向上移动非常明显。并且通过调整?w的取值，可以使存在安装误差情况下的接触轨迹与无安装误差时鼓形齿的接触轨迹重合，说明可以通过调整鼓形中点的位置来控制接触轨迹位置，这对于齿轮的高精度安装和调整有着重要意义。

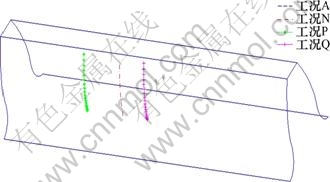
图11  鼓形中点位置对鼓形齿轮接触轨迹的影响

Fig.11  Effect of drum midpoint to contact path

3.3  实验分析

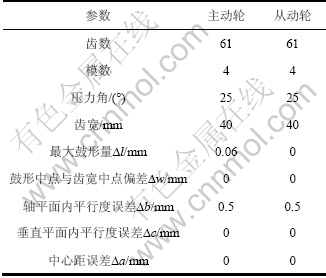
应用商用有限元软件CATIA仿真分析结果与实验进行对比，验证本文提出的修形方法的可行性。为方便进行实验，采用实验室已有的齿轮箱的一对齿轮，对主动轮进行鼓形修形，从动轮不修形，各项修形参数和安装误差如表3所示。

表3  鼓形参数与安装误差取值表

Table 3  Table of drum parameter and alignment errors values

将主动轮修形的齿轮对安装到中心距可调的齿轮箱中，如图12所示。调节齿轮安装误差为轴平面(由两相啮合齿轮轴所决定的平面)内的平行度误差，在相啮合齿轮齿面涂上红丹粉，让齿轮对在轻载条件下(负载为磁粉制动器)进行啮合传动，一段时间后得到齿面接触印痕如图13所示。

图12  加载接触分析实验装置

Fig.12  Loaded contact analysis experiment device

图13  接触印痕

Fig.13  Contact prints

按前面所述的方法，建立有安装误差、含齿向修形的齿面方程，进行啮合接触分析，把得到的离散点导入到CATIA中建立齿轮接触可视化模型如图14  所示。

图14  加载接触分析接触轨迹

Fig.14  Contact path of loaded contact analysis

将图13与图14进行对比发现：齿轮对滚的接触印痕与加载接触分析的接触印痕在位置上基本相符的，说明本文给出的理论方法是正确的。

4  结论

(1) 齿轮中心距误差对鼓形齿接触轨迹的偏移基本上没有影响；轴平面内及垂直平面内平行度误差都会使鼓形齿的接触轨迹产生偏移。

(2) 垂直平面轴线的平行度误差对接触轨迹的影响较轴平面内平行度误差要大得多。

(3) 在相同的安装误差下，随着鼓形量增大，接触轨迹逐渐向齿轮齿宽中间位置靠近，但是它对鼓形量的敏感度逐步降低，说明只利用鼓形量对鼓形齿接触轨迹的控制作用是有限的。

(4) 鼓形中点的位置将直接影响鼓形齿的接触轨迹的位置。故在生产实践中可以通过调整鼓形中点的位置来精确控制接触轨迹的位置，使接触轨迹处于最佳位置，这是本文提出的等半径圆弧鼓形修形齿面的优点之一。

参考文献：

[1] 何大为, 方宗德. 航空圆柱齿轮传动齿向修形优化设[J]. 西北工业大学学报, 1992, 10(3): 323-328.
HE Da-wei, FANG Zong-de. Air cylindrical gear tooth modification to optimize the design[J]. Journal of Northwestern Polytechnical University, 1992, 10(3): 323-328.

[2] 孙月海, 张策, 陈树勋, 等. 直齿轮齿廓修形的实验研究[J]. 中国机械工程, 2003, 14(8): 634-636.
SUN Yue-hai, ZHANG Ce, CHEN Shu-xun, et al. Spur gear tooth profile modification experimental study[J]. China Mechanical Engineering, 2003, 14(8): 634-636.

[3] 朱传敏. 齿轮修形的优化设计与试验研究[J]. 机械工程学报, 1998, 34(4): 63-68.
ZHU Chuan-min. Gear tooth shape optimal design and experimental research[J]. Chinese Journal of Mechanical Engineering, 1998, 34(4): 63-68.

[4] Lin H H, Townsend D P, Oswald F B. Profile modification to minimize spur gear dynamic loading[C]//Lin H H. Proc 1989 Int Power Transm Gearing Conf: New Technol Power Transm 90’s. Chicago: American Society of Mechanical Engineers (ASME), 1989: 455-465.

[5] Lin H H, Oswald F B, Townsend D P. Dynamic loading of spur gears with linear or parabolic tooth profile modifications[J]. Mechanism and Machine Theory, 1994, 29(8): 1115-1129.

[6] Fatih K, Stephen E. Influence of tip relief modification on the wear of spur gears with asymmetric Teeth[J]. Tribology Transactions, 2008, 51(5): 581-588.

[7] Alfonso F, Hiroyuki N, Litvin F L, et al. Computerized design of modified helical gears finished by plunge shaving[J]. Comput Methods Appl Mech Engrg, 2010, 199: 1677-1690.

[8] Litvin F L, Alfonso F, Ignacio G P. Modified involute helical gears computerized design, simulation of meshing and stress analysis[J]. Comput Methods Appl Mech Engrg, 2003, 192: 3619-3655.

[9] Litvin F L, Daniele V, Ken Y, et al. Reduction of noise of loaded and unloaded misaligned gear drives[J]. Comput Methods Appl Mech Engrg, 2006, 195: 5523-5536.

[10] Litvin F L, Feng P H, Lagutin S A, et al. Helical and spur gear drive with double crowned pinion tooth surfaces and conjugated gear tooth surfaces: United States, US 6205879B1[P]. 2001-03-27.

[11] Litvin F L, Chen N X. Computerized design and generation of low-noise helical gears with modified surface topology[J]. Mechanical Design Transactions of the ASME, 1995, 117(2A): 254-261.

[12] Litvin F L, Lu J, Townsend D P, et al. Computerized simulation of meshing of conventional helical involute gears and modi?cation of geometry[J]. Mechanism Machine Theory, 1999, 34(1): 123-147.

[13] 朱孝录, 刘鹄然. 齿轮在弯扭偏载下的齿向修形[J]. 机械, 1993, 20(4): 15-18.

ZHU Xiao-lu, LIU Hu-ran. Gear to bending and torsion under eccentric loading axial modification[J]. Machinery, 1993, 20(4): 15-18.

[14] 吴序堂. 齿轮啮合原理[M]. 北京: 机械工业出版社, 1982: 163-165.

WU Xu-tang. Principle of gear meshing[M]. Beijing: China Machine Press, 1982: 163-165.

[15] Litvin F L, Lian Q, Kapelevich A L. Asymmetric modified spur gear drives: Reduction of noise, localization of contact, simulation of meshing and stress analysis[J]. Comput Methods Appl Mech Engrg, 2000, 188(3): 363-390.

[16] 薛定宇, 陈阳泉. 高等应用数学问题的MATLAB求解[M]. 北京: 清华大学出版社, 2004: 176-179.

XUE Ding-yu, CHEN Yang-quan. Advanced applied mathematics problem solving by MATLAB[M]. Beijing: Tsinghua University Press, 2004: 176-179.

(编辑 杨幼平)

收稿日期：2011-07-12；修回日期：2011-09-11

基金项目：国家重点基础研究发展计划(“937”计划)项目(2011CB706800)；国家自然科学基金资助项目(50875263)；中南大学研究生学位论文创新基金资助项目(2010ssxt176)

通信作者：唐进元(1962-)，男，湖南永州人，博士，教授，从事数字化制造，齿轮动力学研究；电话：0731-88876350；E-mail: jytangcsu@163.com