
Intelligent prediction model of matte grade in copper flash smelting process
GUI Wei-hua(桂卫华), WANG Ling-yun(王凌云), YANG Chun-hua(阳春华),XIE Yong-fang(谢永芳), PENG Xiao-bo(彭晓波)
School of Information Science and Engineering, Central South University, Changsha 410083, China
Received 26 December 2006; accepted 28 June 2007
Abstract: Due to the importance of detecting the matte grade in the copper flash smelting process, the mechanism model was established according to the multi-phase and multi-component mathematic model. Meanwhile this procedure was a complicated production process with characteristics of large time delay, nonlinearity and so on. A fuzzy neural network model was set up through a great deal of production data. Besides a novel constrained gradient descent algorithm used to update the parameters was put forward to improve the parameters learning efficiency. Ultimately the self-adaptive combination technology was adopted to paralleled integrate two models in order to obtain the prediction model of the matte grade. Industrial data validation shows that the intelligently integrated model is more precise than a single model. It can not only predict the matte grade exactly but also provide optimal control of the copper flash smelting process with potent guidance.
Key words: copper flash smelting process; matte grade; multi-phase and multi-component model; fuzzy neural network; constrained gradient descent algorithm
1 Introduction
The copper flash smelting process is one of the complicated pyrometallurgical processes. A lot of fruitful researches have been done for the online mechanism model of the copper flash smelting process. Not only the matte grade and distribution of accessory element can be predicted[1], but also the online control is realized for the industry[2-3]. But this model is established on the rigorous theory of metallurgical physical chemistry. In the practical production there are lots of uncertain factors such as many variations of mineral resources and great fluctuation of the industrial status, so the practical production process deviates from the applicable condition of the mechanism model. This model can not satisfy the requirement of industrial production completely.
Furthermore the matte grade is one of the comprehensive indexes in the copper flash smelting process when the amount of the treated material is invariable in the copper flash smelting furnace. The stable matte grade is important to the smelting, converting and the production of sulfuric acid[4]. However, the matte grade is detected later more than 1 h when the copper flash smelting process is finished, so it can not supervise the production manipulation in time. Consequently it is very significant to predict the matte grade online for stabilizing the copper flash smelting production and improving the product quality. WAN et al[5] established the model of the flash smelting furnace based on the neural network and adopted it to predict the technological index and yield. WAN et al[6] also set up the dynamic quality model of the nickel flash smelting process by adopting Takagi-Sugeno fuzzy model. Also its structure and parameter identification were discussed. But these two approaches are not guided according to the mechanism of reaction process then the predicted technological index will be not precise.
The idea of intelligent integrated modeling is unique when it is adopted to deal with the information of complex process that is characterized by intricate internal mechanism such as nonlinearity, uncertainty and large time delay. Industrial data can be used for system identification and neural network modeling. The experience knowledge can also be taken as the basis of expert experience and fuzzy logic modeling. In addition, the cognition to the mechanism of industrial process is the premise of the mechanism modeling. Therefore these diverse information provide convenience for the integration of different modeling methods[7-10].
In this study the matte grade of the copper flash smelting process was predicted. Firstly the mechanism model based on multiphase and multi-component model was discussed; secondly a fuzzy neural network model was set up by production data and rules in order to overcome the nonlinear dynamic characteristic in the process. Due to the low parameter learning efficiency, a constrained gradient descent algorithm of the parameter learning was proposed in the fuzzy neural network. Finally the self-adaptive combination technology was adopted to paralleled integrate the two models in order to obtain the prediction model of the matte grade.
2 Mechanism of matte grade based on multi-phase and multi-component model
In the copper flash smelting process, the fine particles of dry concentrate and flux are mixed with the oxygen-enriched air at the nozzle of the flash smelting furnace, then are injected into the furnace from the top of the reaction tower and react. The blending melts of the molten sulfide and oxide fall down to the bottom of the reaction tower, then they are gathered, precipitated and separated in the precipitation pool. Finally the matte and slag are formed respectively.
The copper flash smelting process is a typically hermetically sealed container pyrometallurgical process. This chemical reaction is extremely complicated and the reaction substances have three phases such as solid, liquid and gas. Generally the mathematic model of the multiphase and multi-component chemistry equilibrium is established through Brinkley principle that is also called equilibrium constant method. Its basic idea is that the whole components contained in each phase are divided into independent components and auxiliary components in the equilibrium system. The elements that compose the independent components should include the whole elements in this system and the number of independent components should be equal to the sum of the kinds of elements contained in the system when the independent component is chosen. So the amount of substance of the whole auxiliary components in the equilibrium system can be described as the function of the amount of substance of independent components. The amount of substance of the auxiliary components can be obtained as long as the amount of substance of the independent components was acquired. Hence the multiphase and multi- component equilibrium model based on Brinkley principle can be used to compute the matte grade when the equilibrium model reaches balance in the copper flash smelting process.
If the temperature, pressure and the amount of substance of each element are given in the sealed system, the equilibrium state of this system will be determined. The key point of equilibrium constant method is that all the chemistry reaction reaches balance at the same time when the system reaches balance. The different components in each phase are associated with a group of complex united equations through equilibrium constant. The amount of substance of each component in the equilibrium system can be obtained through solving the united equations and this is the basic idea of equilibrium constant method. There are Goto method, reaction course method and so on according to the different concrete disposing methods. All the equilibrium constant methods are developed based on Brinkley principle. The detailed introduction of the general principle for equilibrium constant method can be seen in Ref.[4].
The copper flash smelting process is a typical multi-phase and multi-component reaction process in the hermetically sealed container. According to the multi-phase and multi-component mathematic model of the copper flash smelting established by the balance constant method, the amount of fine concentrate, slag fine concentrate, siliceous concentrate, indeterminate material, oxygen-enriched air and the composition of each component are substituted into this mathematic model, respectively. Then the calculated amount of substance of Cu, Fe, S, O, As and Zn elements in the matte are substituted into the mechanism model of matte grade:
 (1)
(1)
where mi is the amount of substance of each element, ai is the relative atomic mass of each element.
The static mathematic model of matte grade based on metal equilibrium equation can reflect the industrial status, but there are certain errors in the calculated result of the model inevitably.
3 T-S fuzzy neural network identification model of matte grade
3.1 T-S fuzzy neural network model
Although the matte grade based on multiphase and multi-component model is established on the basis of rigorous theory of metallurgical physical chemistry, there will be some phenomena for example industrial status fluctuates, the smelting process deviates from equilibrium system, the charge material and oxygen- enriched air are not mixed homogeneously, and the distribution temperature is lack of balance in the reaction tower in the practical production. So there is a great difference between the practical reaction and ideal chemical equilibrium. The exact analytic solution can not be obtained through the mechanism model. However there is a great deal of industrial data and expert experience in the production field. The stable production data that have the characteristic of sensitivity and real time implicate the mechanism and rule of the reaction process and can reflect the reaction practice to a certain extent. It is feasible to adopt fuzzy neural network to set up the prediction model of the matte grade.
The intelligent model of matte grade is established by T-S fuzzy neural network that is widely adopted in the complicated nonlinear system modeling process. The fuzzy neural network integrates the neural network with the fuzzy logic. It not only has the strong structural knowledge expression capability of fuzzy logic inference, but also has the powerful self-learning capability and data processing capability of neural network.
The predicted matte grade is influenced by many factors that have nonlinear relationship with the matte grade in the copper flash smelting process. However, there are a great deal of industrial data that can be analyzed in the industrial field. Meanwhile the convenience of the data acquirement and the correlation among variables should be regarded. The correlation not only among variables but also between variables and matte grade was studied. The variables that have less correlation with the matte grade will be eliminated. Therefore the complexity of the model can be reduced potentially under the premise of not losing important input variables information. The input variables of the fuzzy neural network model are the amount of air, oxygen in the reaction tower, flux, dust, cupreous ratio of dry fine concentrate, slag fine concentrate, siliceous concentrate and indeterminate material.
Usually the fuzzy neural network model is a four-layer feedforward network[11]. The nodes in the first layer transmit the input information to the next layer directly. Each node in the second layer acts as a membership function. The Gaussian function is selected as a membership function that divides the input information. The nodes in the third layer perform the fuzzy T-norm operations, and each node represents a rule. The antecedent rules are fuzzy variables and the consequents are equations described through precise variables. The rule is expressed as follows:
Rule j:
If x1 is A1j, x2 is A2j … and xn is Anj,
Then
 (2)
(2)
where xi(i=1, 2,…, n) and y are input and output variables respectively; Aij (j=1, 2, …, p) is the fuzzy set that is defined as the universe of discourse Ui; αij is the consequent parameter of the rule; n is the number of input variables and p is the number of rules.
The node in the fourth layer performs the defuzzification operation that applies centroid method. wi is the connective weight between the rule layer and the defuzzification layer. Its output expression is
 (3)
(3)
where 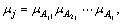
 is the membership
is the membership
function of the universe of discourse Ui.
3.2 Constrained gradient descent algorithm of model’s parameter updating
BP algorithm and gradient descent algorithm are usually adopted to update the membership function parameters of fuzzy neural network[12-14]. Always they are prone to fall into the local minimum in the parameters’ learning process of fuzzy neural network owing to the intrinsic limitation of gradient descent algorithm. Besides if the surrounding area of the solution is smooth, the parameters will learn more slowly. Due to the low parameters learning efficiency of conventional T-S fuzzy neural network model, the established network model can not satisfy the industrial process with the characteristic of large time delay for real time. In order to improve the conventional parameters learning algorithm, the constrained gradient descent algorithm is proposed to update the model’s parameters. This learning algorithm not only reserves the merit of the traditional gradient descent algorithm, but also improves its scarcity.
Generally speaking, the validity of fuzzy logic rule must be guaranteed, i.e. the membership grade of the crossover point of two membership function curves whose centers are adjacent must be bigger than 0.5 while designing the fuzzy logic rule of T-S fuzzy neural network, namely the ε-completeness of fuzzy logic must be 0.5[15]. In order to guarantee this trait of fuzzy logic rules and each logic rule to exert its self-function effectively according to the inputs of the model, a constraint function is proposed next.
In the membership function layer of T-S fuzzy neural network model, Gaussian function is chosen as the membership function, i.e:

i=1, 2, …n; j=1, 2, …, p (4)
where cij and σij are the center and width of Gaussian membership function respectively. From Fig.1, it can be seen that the crossover point xi0 of that two curves can be obtained through the following equation when two crossed membership functions whose centers are adjacent operate on the input variable xi simultaneously:

Fig.1 Two Gaussian membership function adjacent to junction
 (5)
(5)
then
 (6)
(6)
The membership grade of the crossover point must not be smaller than 0.5, i.e.  ≥0.5. So the following expression can be obtained:
≥0.5. So the following expression can be obtained:
 ≤ln2 (7)
≤ln2 (7)
or
 ≤ln2 (8)
≤ln2 (8)
From the above bilateral neighborhood of the crossover point xi0 in Fig.1, it can be seen that the span of the satisfied xi0 can be expressed as the following two inequations:
xi0≤ (9)
(9)
xi0≥ (10)
(10)
Incorporating the two constraint conditions of the Eqns.(9) and (10), the constraint function f can be obtained as follows:
 ≥0 (11)
≥0 (11)
When considering the proposed constrained gradient descent algorithm, the membership function parameters of fuzzy logic are not updated in accordance with this algorithm firstly, but updated by adopting the conventional unconstrained gradient descent algorithm. If the updated parameters are in the feasible region as defined in Eqn.(11), then they are deemed acceptable. Otherwise these parameters need to be updated again by using the constrained gradient descent algorithm until the updated parameters are in the feasible region.
For a group of training data  the input x is the n dimension vector {x1, x2, …, xn},
the input x is the n dimension vector {x1, x2, …, xn},  is the desired output and y is the practical output of the model. The following objective function is defined as the performance index of the training data, where L is the group number of the training data:
is the desired output and y is the practical output of the model. The following objective function is defined as the performance index of the training data, where L is the group number of the training data:
 (12)
(12)
For Gaussian membership function, the training process of fuzzy neural network is that the membership function parameters cij and σij are regulated continuously through minimizing the value of the objective function E. The parameters of membership function are updated by using the following conventional gradient descent algorithm firstly:
 (13)
(13)
 (14)
(14)
where k is the kth training epoch; ηc and ησ are the learning step size.
Next, the completeness value of fuzzy logic must be verified not less than 0.5 at least. At the kth training epoch, the following formula can be obtained according to Eqn.(11):
 cij(k+1)-ci(j+1)(k+1)≥0 (15)
cij(k+1)-ci(j+1)(k+1)≥0 (15)
If Eqn.(15) is satisfied and the performance index of the objective function E achieves the appointed value at the kth training epoch, the updated parameters at the current epoch are feasible solutions. Otherwise the parameters must be updated again in accordance with the following algorithm.
1) Keeping σij(k+1) invariable, i.e. the width of Gaussian membership function is invariable, cij(k+1) is recalculated as follows:
 (16)
(16)
2) Keeping cij(k+1) invariable, i.e. the center position of Gaussian membership function is invariable, σij(k+1) is recalculated as follows:
 (17)
(17)
3) cij(k+1) and σij(k+1) will be held invariable respectively. Then they will be updated iteratively by using Eqns.(16) and (17) until the feasible solutions that satisfy the constraint condition are obtained.
Adopting the training procedure of the fuzzy neural network[16] and the improved parameters updating algorithm proposed in this study, the fuzzy neural network model fulfilling the precision requirement is obtained.
4 Intelligent integrated model of matte grade
There are complicated relationship among the matte grade and the amount of fine concentrate, air, oxygen in addition to the great error in the collected data in the copper flash smelting process. The predicted matte grade will not be accurate if the fuzzy neural network model is only used for modeling. The material balance based on multi-phase and multi-component can analyze how these variables influence the matte grade quantitatively. But it is difficult to acquire the precise analytic model from the global scale and to determine the parameters of the material balance equations because of some uncertain factors such as variation of mine resource.
Therefore it is necessary to adopt intelligent integrated modeling method to establish the intelligent prediction model of the matte grade. The mechanism model should be paralleled integrated with the fuzzy neural network model and the optimal integrated model is established through determining the weights of different submodels in real time. Then their advantages can complement each other and the matte grade can be predicted exactly. The frame of the integrated model is shown in Fig.2 and the integrated model is expressed as follows:

Fig.2 Frame of integrated model
 (0<w1, w2<1) (18)
(0<w1, w2<1) (18)
where w1 and w2 are the weights of the submodels; y is the output of the integrated model; yk1 and yk2 are the outputs of the mechanism model and fuzzy neural network model of the matte grade respectively. Finally the optimal integrated model is founded through determining the weights.
The following quadratic programming is set up in order to minimize the prediction error:
 , (19)
, (19)
where  is the desired output.
is the desired output.
The generalized Lagrangian function of the quadratic programming is constructed as follows:
 (20)
(20)
where λ is the Lagrangian multiplier and K is the group number of input data. Its extreme points should satisfy  . The partial derivatives of w1, w2 and λ are taken in it respectively and a group of equations about these parameters are obtained. Then the prediction value of each submodel and the practical value are substituted into these equations. The values of w1 and w2 can be calculated through resolving these equations so that the optimal integrated model whose error is the minimum can be obtained.
. The partial derivatives of w1, w2 and λ are taken in it respectively and a group of equations about these parameters are obtained. Then the prediction value of each submodel and the practical value are substituted into these equations. The values of w1 and w2 can be calculated through resolving these equations so that the optimal integrated model whose error is the minimum can be obtained.
5 Simulation
Based on the prediction model of the matte grade, 154 groups of industrial data collected from the practical production were used for simulation analysis under the same operation condition. The first 100 groups were chosen as the training data for fuzzy neural network and the last 54 groups were chosen as the validation data, meanwhile as the testing data for the mechanism. The simulation results of different models are shown in Figs.3-6. The dashed line denotes the practical value of matte grade and the solid line denotes the prediction value of matte grade.

Fig.3 Prediction result of mechanism model

Fig.4 Prediction result of traditional fuzzy neural network

Fig.5 Prediction result of improved fuzzy neural network

Fig.6 Prediction result of integrated fuzzy neural network
From the simulation result of the model prediction, the prediction precision of the mechanism model can not satisfy the requirement of the practical application due to the complexity of reaction mechanism, the hypothesis and simplification of modeling. When the matte grade is predicted by adopting a single fuzzy neural network model, the prediction precision of fuzzy neural network whose parameters updating algorithms are improved is better than the traditional fuzzy neural network model.
The mean square root error is reduced from 0.002 6 to 0.002 1 and the training time of model is decreased from 22.8 s to 12.4 s. When the matte grade is predicted through the intelligent integrated model that contains the mechanism model and fuzzy neural network model as well as taking the mechanism as the guidance, the precision of integrated model is much more accurate than a single model apparently and the mean square root error is decreased to 0.001 6. The fitness precision of integrated model that has stronger generalization ability is more exact than a single model.
6 Conclusions
1) Aiming at the complex industrial process of copper flash smelting, the matte grade of the copper flash smelting process is predicted. The multiphase and multi-component model and the fuzzy neural network model of matte grade are established respectively, then the intelligent prediction model is set up by adopting self-adaptive combination technology to integrate these two models.
2) The fuzzy neural network in this integrated model is investigated. Based on the current gradient descent algorithm of parameter updating procedure, a constraint function is introduced as the parameters learning guidance due to the low parameter learning efficiency and slow convergent rate of conventional network. The prediction precision of the network model whose parameters learning algorithm is improved is better than the conventional network model obviously. Moreover the convergent rate of parameters is increased and the training time is shortened.
3) The simulation results of the industrial data show that the intelligent integrated model can restrain the fluctuation of industrial instance effectively and the prediction precision of matte grade is enhanced. So it can supply the optimal control of copper flash smelting process with potent guidance.
References
[1] TAN P F, ZHANG C F. Computer model of distribution behavior of accessory elements in copper smelting [J]. Acta Metallurgica Sinica, 1997, 33(10): 1094-1100.
[2] HUANG Ke-xiong, LI Shu-hua, YIN Ai-yun, MEI Xiao-zhi. Computer simulation of Guixi flash furnace process for copper matte smelting [J]. Journal of Central South University of Technology, 1996, 27(2): 173-176.
[3] SANCHEZ C V M, VALERA G J A, FLORES P P, PEREZ T M. Copper flash smelting mass balance calculations using genetic algorithms [J]. Journal of the Minerals Metals and Material Society, 2004, 56(11): 178-179.
[4] ZHU Zu-ze, HE Jia-qiang. The modern copper metallurgy [M]. Beijing: Science Press, 2003. (in Chinese)
[5] WAN W H, WAN B W, YANG J Y. Study of neural network quality models and steady-state optimizing control for nickel flash smelting furnace [J]. Acta Automatica Sinica, 1999, 25(6): 800-803.
[6] WAN W H, WAN B W, SHI W X, YANG J Y. Fuzzy dynamic quality models and control of nickel flash smelting process [J]. Journal of Xi’an Jiaotong University, 2000, 34(3): 54-59.
[7] LI Jie, KONG Ling-shuang, YANG Chun-hua. Raw mix slurry quality prediction model used for alumina sintering production process [J]. The Chinese Journal of Nonferrous Metals, 2006, 16(3): 536-541. (in Chinese)
[8] RUNKLER T A, GERSTORFER E, SCHLANG M, JUNNEMANN E, HOLLATZ J. Modeling and optimization of a refining process for fibre board production [J]. Control Engineering Practice, 2003, 11(11): 1229-1241.
[9] LI Y G, GUI W H, CHEN F. Multiple neural networks based on factor analysis and its application in soft sensor [J]. Information and Control, 2004, 33(2): 141-144.
[10] PLAMEN P A, DIMITAR P F. An approach to online identification of Takagi-Sugeno fuzzy models [J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cyberbetics, 2004, 34(1): 484-498.
[11] MACROS J A, JOSE M C, EDUARDO G S, MANUEL J L, DIMITRIADIS Y A, LOPEZ C J. Automatization of a penicillin production process with soft sensors and an adaptive controller based on neuro-fuzzy systems [J]. Control Engineering Practice, 2004, 12(9): 1073-1090.
[12] RUTKOWSKI L, CPALKA K. Designing and learning of adjustable quasi-triangular norms with applications to neuro-fuzzy systems [J]. IEEE Transactions on Fuzzy Systems, 2005, 13(1): 140-151.
[13] PARK B J, PEDRYCZ W, OH S K. Fuzzy polynomial neural networks: Hybrid architectures of fuzzy modeling [J]. IEEE Transactions on Fuzzy Systems, 2002, 10(5): 607-621.
[14] LIU J Q, SAN Y, WANG Z C. Modeling of complex large-scale system using fuzzy neural networks [J]. Journal of System Simulation, 2001, 13(3): 304-307.
[15] WANG W, ISMAIL F, GOLNARAGHI F. A neuro-fuzzy approach to gear system monitoring [J]. IEEE Transactions on Fuzzy Systems, 2004, 12(5): 710-723.
[16] NAYAK P C, SUDHEER K P, RANGAN D M, RAMASASTRI K S. A neuro-fuzzy computing technique for modeling hydrological time series [J]. Journal of Hydrology, 2004, 291(1): 52-66.
Foundation item: Project(60634020) supported by the National Natural Science Foundation of China; Project(2002CB312200) supported by the National Basic Research and Development Program of China
Corresponding author: WANG Ling-yun; Tel: +86-731-8830394; E-mail: susanwling@hotmail.com
(Edited by LI Xiang-qun)