`DOI：10.19476/j.ysxb.1004.0609.2019.04.05

6061铝合金与H13模具钢固体界面接触换热系数的反分析求解

刘志文^{1, 2}，李落星²，易  杰²，王  冠²

(1. 南华大学 机械工程学院，衡阳 421001；

2. 湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

摘  要：采用FORTRAN语言建立固体界面一维反热传导的计算程序，结合自制的热电偶测温实验装置，等效研究6061铝合金挤压型材在线弯曲过程中与H13模具钢界面的瞬态换热行为，探讨初始温度、接触载荷、表面粗糙度和热流方向对接触换热系数的影响。结果表明：瞬态换热系数在开始接触的短时间内(5 s)急剧上升，然后缓慢增大至某一稳定值。当界面平均接触温度从111.5 ℃增大到211.5 ℃时，接触换热系数迅速增加。进一步提高界面平均接触温度，接触换热系数增加速率下降；随着表面粗糙度的增大，接触换热系数逐渐减小，在1.66~2.05 μm范围内影响最为显著。随着载荷的增加，接触换热系数逐渐增大，敏感性逐渐下降；热流方向从铝合金到H13钢时的接触换热系数明显要比H13钢到铝合金的接触换热系数大。

关键词：6061铝合金；H13钢；反热传导；接触换热系数；影响因素

文章编号：1004-0609(2019)-04-0700-09　　     中图分类号：TG 301　　     文献标志码：A

铝合金具有低密度、比强度和比刚度高、易回    收和无污染等一系列优点，是汽车轻质化的理想材  料^[1-2]。型材是变形铝合金在车身结构应用中的主要形式。汽车用铝合金型材通常需要进行后续弯曲加工，传统冷弯加工会产生回弹和截面畸变等问题，很难达到装配精度要求。针对以上问题，本文作者课题组前期发明了一种挤压-弯曲一体化加工新技术^[3-4]。通过在常规卧式挤压机出口位置添加一套位置和旋转角度可调、并且与型材外轮廓相适应的导向辊轮装置，使型材挤出模口后在温热状态下直接发生弯曲变形，从而避免回弹和截面畸变等问题。挤压型材在线弯曲过程中，辊轮与型材的接触换热系数会影响弯曲型材横截面的温度场和应力分布的均匀性，进而影响回弹和截面畸变的大小。数值仿真是研究挤压型材在线弯曲问题的重要手段。辊轮与型材之间的固体接触换热系数是影响仿真精度重要的边界条件，受固体温度、接触载荷、表面粗糙度和材料类型等因素影响，要准确预测和求解十分困难^[5-7]。目前，在成形数值仿真中，接触换热系数主要通过查表或经验获取，导致仿真精度较低。因此，辊轮与型材界面传热系数的精确求解，对挤压型材在线弯曲过程的数值模拟以及成形工艺参数的优化等起着重要作用，仿真中辊轮与型材之间采用的换热边界条件应能尽可能的接近实际情况。

近年来，国内外学者采用稳态热流法对不同材料间的接触换热系数进行了大量研究，获得一些有价值的实验数据^[8-12]。而实际热加工是材料与工模具的瞬态接触过程，其物理机制与稳态接触换热有很大区别，因而不能采用稳态法对其进行求解。现有文献对瞬态接触换热过程的研究甚少，BAI等^[13]采用一维反热传导方法结合数值仿真技术研究了接触载荷、介质厚度和表面粗糙度对Ti-6Al-4V燃气轮机叶片热锻过程中工件与H13模具钢界面换热系数的影响。TARIQ等^[14]设计一维轴向换热实验结合反分析方法研究了表面粗糙度和接触载荷对铜、黄铜和不锈钢材料接触换热系数的影响。FIEBERG等^[15]利用红外测温仪对不同温度的铝合金和钢接触后的瞬态温度场进行测量，通过求解瞬态热传导方程得到瞬态接触换热系数。邢磊等^[16]利用自制的瞬态接触换热系数测量装置研究了TP2铜与3Cr2W8V模具钢的瞬态接触换热行为。ABDULHAY等^[17]建立了与界面压力相关的USIBOR1500P板料与模具界面间的接触热阻函数关系式。到目前为止，6061铝合金与H13热作模具钢的瞬态接触换热方面的研究还未见相关报道。

本文采用FORTRAN语言建立固体界面一维传热的反求程序，结合自制的热电偶测温试验装置，等效研究挤压型材在线弯曲过程中6061铝合金与H13模具钢的瞬态接触换热过程，获得不同工艺条件下的界面温度及平均热流量，系统探讨初始温度、接触载荷、表面粗糙度和热流方向等工艺条件对接触换热系数的影响规律。研究结果可为铝合金挤压型材在线弯曲过程中接触换热及数值模拟热边界条件的确定提供理论基础。

1  固体界面反热传导算法

反热传导问题与正传热问题相反，反热传导算法的求解过程是通过两接触固体内部已知的温度场来反求不知道的边界条件。采用反热传导算法求解界面换热系数时，首先通过两接触固体内部已知的温度场来计算界面的热流，再通过式(1)计算界面换热系数：

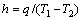                               (1)

式中：h是界面换热系数，W/(m²×K)；q为界面热流，W/m²；T₁和T₂分别是两接触固体的表面温度，K。

在反传热求解固体界面换热系数时，每次迭代计算都需要正向求解温度场M次，所以在设计实验方案时，通常尽量将几何模型简化，使固体界面传热满足一维传热模型，温度只有沿轴向的变化，而不考虑其他方向的变化，且忽略对流及辐射所带来的影响，能大幅减少正传热求解的计算量，从而提高反求的效率。因此，本文采用固体一维传热模型等效表征挤压型材在线弯曲过程辊轮与型材的接触换热行为。一维反热传导算法的求解过程中，根据BECK等^[18]提出的非线性系列估算法可以将随时间变化的热流q(t)分成若干个时间间隔的离散值(q_i =q₁, q₂,…, q_N)，如图1(a)所示。另外，由于两固体内部热电偶温度的响应滞后于固体界面的温度变化，因此在求解每个Δθ时间间隔内的热流q_i时，假设q_i在RΔθ时间间隔内为一个常数，R为未来时间步长，如图1(b)所示，未来时间步长R的正确选择有助于改善反求算法的稳定性。

图1  热流被离散求解的情况

Fig. 1  Schematic illustration of discrete heat fluxes in inverse algorithm

采用反热传导算法求解界面热流时，需要设置相应的计算参数，包括未来时间步长R、热流计算的时间步长Δθ、迭代收敛误差判据、初始温度场以及初始猜测的热流等。参数设置完成后，开始反算求解，建立的反热传导算法流程如图2所示。当第一个Δθ时间间隔内的热流q₁被迭代计算得到后，循环计算下一个Δθ时间间隔内的热流q₂，周而复始，直到每一个Δθ时间间隔内的热流q_i被全部计算得到为止。其中每一个Δθ的热流q_i是通过测量温度与计算温度误差值最小的判据迭代计算获得，可用式(2)表示：

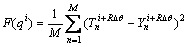               (2)

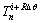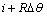式中：M是求解的未知热流数；为在时间内基于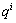的计算温度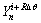；是在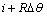时间内的测量温度；函数F是通过迭代计算的目标函数。

在每一次迭代求解热流q_i过程中，Δq通过下式计算：

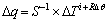                           (3)

式中：S是敏感系数，被定义为在接触固体内部某位置的温度随着单位热流变化的响应，它可以通过数值差分的方法近似计算得到，其表达式如下：

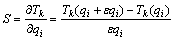                 (4)

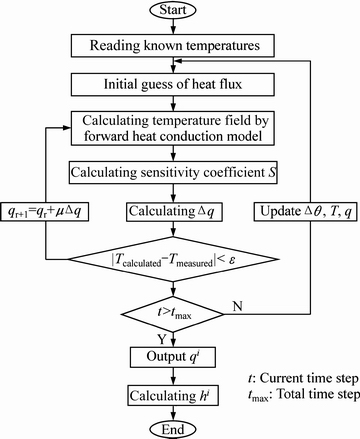
图2  固体界面反热传导算法流程图

Fig. 2  Flow chart of inverse heat conduction algorithm for solid interfaces

式中：i=1, 2, …, N；k=1, 2, …, P；ε是一个数值差分计算采用的很小值，一般取值0.001。

在迭代计算热流时，通过一个迭代值Δq更新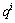，一个接近1值的阻尼系数μ被使用来稳定计算结果，迭代计算方程如式(5)所示：

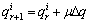                              (5)

当式(2)中测量的温度与计算的温度差值满足给定的收敛误差值时，如≤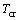，当前时间步长的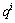可以被反计算得到。然后，将此时得到的界面热流值作为计算下一时刻热流值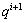时的初始假设值，重复上面的过程，直到所有时刻内的热流q(t)被计算得到为止。本文采用Fortran语言根据前述反热传导理论建立固体界面一维传热的反求程序，获得不同条件下的界面温度及平均热流量，根据式(1)最终计算得到两固体间的接触传热系数。

2  试验方法

界面接触换热系数的反求，首先需设计一维固体界面换热试验，确定模型的初始条件、边界条件及材料热物性参数，然后通过压力试验获取两接触物体内部的温度数据，建立反求模型求解界面温差和热流，从而得到接触换热系数。因此，作为界面换热系数反求必须的已知数据，两固体内部某些点的温度数据需要通过试验测得。

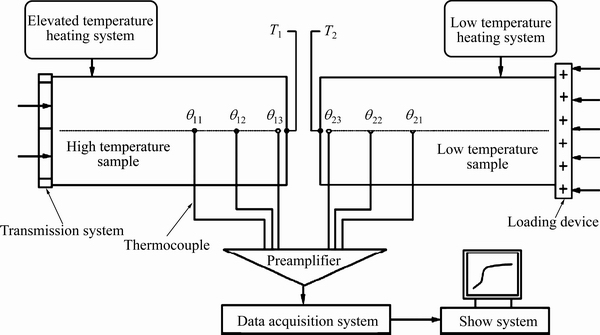
图3  反传热装置工作原理

Fig. 3  Principle diagram of inverse heat transfer device

图3所示为固体界面接触换热试验装置原理图。实验装置由加热系统、传动系统、加载装置、数据采集系统和PC终端机等4部分组成。加热系统采用电磁加热，加热电阻丝在距离试样表面的一定距离采用螺旋方式环绕，最高加热温度可以达到700 ℃以上，温差范围可以控制在 ±2 ℃以内，通过控制功率大小调节试样所需要达到的温度；整个实验在无压条件下进行，传动装置采用简便的手动方式；加载装置的最高载荷可以达到50 MPa；数据采集系统由多通道采集模块、R型热电偶传感器组成。带自动增益的高速A/D 转换卡通过16 通道的前端放大板将测温热电偶的电压信号输入采集软件，实现模拟量与数字量的转换。热电偶一端分别与试样内部待测温度点θ₁₁、θ₁₂、θ₁₃和θ₂₁、θ₂₂、θ₂₃相连，另一端与温度数据采集模块相连，采集模块通过USB转换器将采集温度传入PC终端存储。

实验材料分别为H13模具钢与6061铝合金，设计试样尺寸为直径20 mm，长度50 mm，以使界面接触传热可近似看成一维传热。试样端面的粗糙度通过车削加工获得。在距离试样端面3、10和20 mm处的试样中心轴上分别钻取直径为2 mm、深度为10 mm的热电偶安装孔，方便实验过程中通过温度采集系统实时采集各特征点的温度变化曲线。热电偶在安装孔中使用耐高温硅胶经行密封。为了最大限度地减少与空气的对流换热和辐射换热，使用耐高温石棉对除试样端面外的表面经行密封捆扎，其最外层覆盖铝箔以进一步减小误差大小。

一维传热实验在万能压缩试验机上实现(见图4^[6])，为避免试样接触时发生偏置，对上下横梁首先进行对中调整。试样加热前先将3组耐高温热电偶按图3中的位置安装好，热电偶另一端连接NIUSB- 9213，然后通过电阻丝加热至设定温度。保温快结束时，将温度采集仪与电脑连接好，通过电脑实时监控试样温度，设置好数据采集模块的响应时间为0.1 s，并对其经行校正。当两处热电偶温度差小于0.2 ℃且试样到达预设温度时，通过压缩试验机传动机构推动试样端面快速接触，并按预先设定的载荷由加载装置施加到接触面上。与此同时，温度采集系统通过测温热电偶、前端放大板和A/D 转换卡对试样内部各测温点的温度进行实时采集与显示。

图4  一维固体传热试验装置^[6]

Fig. 4  Photograph of experimental device for one- dimensional heat transfer^[6]

3  分析与讨论

3.1  反热传导方法的验证

通过R型热电偶测得的近端面θ₁₃和θ₂₃两点的温度作为输入条件，利用所建立的反求程序可以计算出远端面θ₁₁和θ₂₁等特征点的温度，然后与实验测得的温度进行比较，验证反求算法的可靠性及准确性。图5所示为不同试验条件下反求温度与实验测量结果的对比图。由图5可知，两种不同接触界面条件下，铝合金试样远端面点的温度反求曲线与实验测量曲线几乎接近一致；与铝合金试样相比，H13钢远端面的温度反求曲线与实验测量曲线在初始接触阶段也吻合较好，超过100 s以后的冷却阶段有一定偏差，反求计算温度略高与实验测量温度，但两者之差在8 ℃以内。造成误差的原因可能有：试样不可避免的与外界环境发生热交换，接触界面间可能存在微小的杂质颗粒以及热电偶的测点位置并不完全处于试样的中心轴线上等，这些因素的存在使得反求计算的温度要略高于实验测量温度。但就整个系统而言，误差在5 %以内，证明了反求结果有足够的精度及可信度。

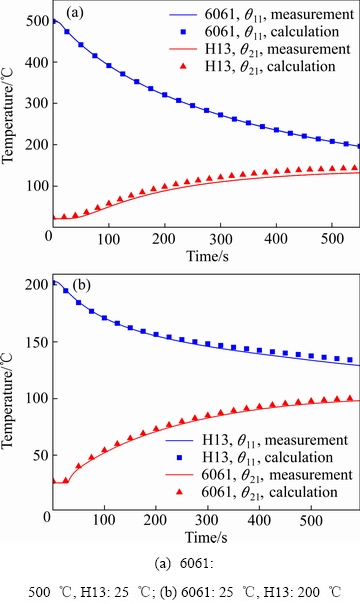
图5  反求计算与实验测量的校核特征点温度曲线

Fig. 5  Comparison of characteristic point temperature measured and calculated at verification position

3.2  温度冷却曲线分析

根据传热学理论，高低温试样接触以后，固体界面将发生剧烈的热量交换，试样内部温度场将重新分布。固体界面换热阶段，反求计算的各特征点温度曲线如图6所示，该结果对应的试验条件为：铝合金试样温度初始为500 ℃，H13钢试样初始温度为25 ℃，H13试样表面粗糙度值R_a=18.38 μm；铝合金试样表面粗糙度值R_a=4.14 μm。由图6可知，铝合金高温试样内部所有特征点的温度都经历了快速下降和相对缓慢下降两个阶段，温度降幅最高达到300 ℃左右，但3个特征点的温度曲线差异相对较小；对于低温试样H13钢，各特征点的温度都先急剧上升到最高值，然后缓慢下降，达到稳定阶段以后与高温试样的温度差异越来越小。然而与高温试样铝合金不同，H13钢低温试样接触端面的温度上升速率最快，首先达到峰值，温度增加到193 ℃；离端面距离越远，上升速率越慢，温升大小相对也较小。这主要是由于铝合金的导热系数远大于H13钢的导热系数，传热性能更好，结果各特征点的温度差异较小。

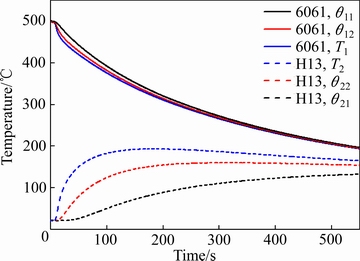
图6  6061铝合金和H13钢接触后特征点温度随时间的变化

Fig. 6  Change of characteristic point temperature with time after contact of 6061 alloy and H13 steel

3.3  初始温度对接触换热系数的影响

图7所示为在相同界面接触条件下温度对接触换热系数的影响。具体的试验条件是：接触载荷为2.5 MPa；H13试样表面粗糙度值R_a=18.38 μm；铝合金试样表面粗糙度值R_a=4.14 μm。由图7可知，不同温度条件下的接触换热系数随时间变化的规律基本一致。高低温试样在开始接触的5 s短时间以内，在接触载荷的作用下界面的微凸体发生弹性或塑性变形，接触面积迅速增大使界面之间发生剧烈的热交换，热流量在短时间内增加到峰值。高温试样界面温度迅速降低，低温试样界面温度快速升高，温度梯度达到最大，使传热系数急剧上升到最高值；之后由于试样温度梯度的减小，传热效率逐渐降低，通过界面的平均热流量开始下降，界面温差也相应降低，但在这段时间内温差降低速率高于平均热流量下降的速率，这种差距会越来越小，这就使得接触传热系数仍呈上升趋势，但上升速率减小；在下一个阶段内，换热系数数值开始下降，这是由于此段时间内通过界面热流量的下降速率开始超过温差的下降速率，致使两者的比值，即h的值开始呈下降趋势。温度对接触换热系数影响十分显著。随着温度的增加，100 s以内接触换热系数增加的速率显著增大。

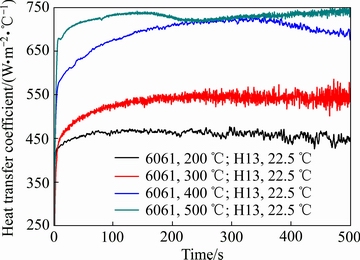
图7  初始温度对接触换热系数的影响

Fig. 7  Effect of initial temperature of 6061 alloy on heat transfer coefficient

图8所示为不同界面平均接触温度下的稳态接触换热系数。由图8可知，当界面平均接触温度为111.5 ℃时，换热系数为474 W/(m²·℃)。随着接触平均温度进一步的增加，接触换热系数逐渐增加。当界面平均接触温度增加到211.5 ℃时，换热系数增加到717 W/(m²·℃)，相比低温增大51.26 %。这主要是由于界面接触温度升高，材料的屈服强度和弹性模量降低，导致加载接触时界面微凸体产生更大的弹塑性变形，使接触面积增大，界面换热能力增加。当界面平均接触温度再增进一步增加到261.5 ℃时，换热系数增大的速率下降，接触换热系数只增加10 W/(m²·℃)。这可能是温度升高，接触面会生成氧化物，氧化物的导热率比母体金属的一般小1~2个数量级，且硬度大于母体金属的，因而导致换热系数随温度的升高缓慢增加。

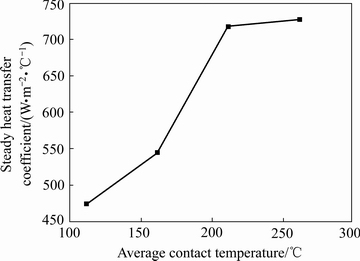
图8  不同界面平均接触温度下6061铝合金和H13钢的稳态接触换热系数

Fig. 8  Steady heat transfer coefficient of 6061 alloy and H13 steel at different average contact temperatures

3.4  表面粗糙度对接触换热系数的影响

表面粗糙度可以用来表征两固体接触表面的凹凸程度。在实际生产中，由于加工精度或制造误差等问题导致试样或模具表面粗糙度发生变化。本文研究假设铝合金试样表面粗糙度值R_a=4.14 μm为不变，接触载荷为2.5 MPa，铝合金试样温度为500 ℃，H13钢试样温度为25 ℃，研究钢制试样表面粗糙度大小对接触换热系数的影响(见图9)。由图9可知，接触换热系数对表面粗糙度的变化十分敏感。随着表面粗糙度的增大，接触传热系数整体曲线上的值逐渐增大，且都在接触之后一段时间内到达一个相对稳定值。图10所示为不同表面粗糙度的平均接触换热系数。由图10可看出，当R_a从1.66 μm增大到71.91 μm时，平均接触换热系数的减少趋势明显不同。R_a在1.66~2.05 μm范围内，粗糙度对接触换热的影响最为显著，换热系数从1246 W/(m²·℃)急剧下降到1123 W/(m²·℃)；R_a在2.05~18.38 μm范围内，下降的斜率减少，换热系数从1123 W/(m²·℃)减少到733 W/m²·℃；R_a在18.38~71.91 μm范围内，换热系数对粗糙度的变化敏感程度进一步降低，换热系数从733 W/(m²·℃)缓慢下降到385 W/(m²·℃)。表面粗糙度的大小对接触热阻有很大的影响，粗糙度越大，表面形貌越不规则，接触界面间的空隙越大，热流在接触界面处的收缩越严重，使接触界面的温差越大，最终导致接触热阻增大，换热系数降低。

图9  粗糙度对H13钢接触换热系数的影响

Fig. 9  Effect of surface roughness on heat transfer coefficient of H13 steel

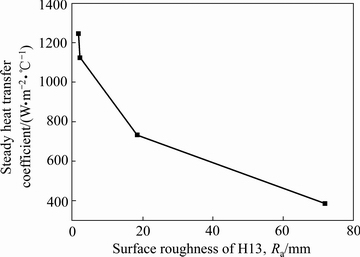
图10  不同表面粗糙度下6061铝合金和H13钢的稳态接触换热系数

Fig. 10  Change of steady heat transfer coefficient at different surface roughness

3.5  接触载荷对接触换热系数的影响

接触载荷也是影响固体界面接触换热的一个重要因素。接触载荷对6061铝合金与H13钢间接触换热的影响如图11所示。具体的试验条件是：6061铝合金试样的初始温度为500 ℃，H13钢试样的初始温度为22.5 ℃，接触载荷分别为1、2.5、5和10 MPa。由图11可知，接触载荷增加，接触换热系数逐渐增大。这是由于载荷的大小会直接影响接触界面处相互接触的微凸体的变形程度。随着载荷的增大，接触界面发生弹塑性变形的微凸体数量逐渐增多，使真实的接触面积增大，换热能力增强，界面间的温差变小，热流密度增大，因此，接触换热系数随着载荷的增加逐渐变大。图12所示为不同载荷下的平均接触换热系数。由图12可知，在低载荷1~2.5 MPa区域范围，接触换热系数随载荷变化的斜率要比5~10 MPa的要大。载荷为1 MPa时，接触换热系数为483 W/(m²·℃)；增加到2.5 MPa时，接触换热系数增加50.5 %；当增加到5 MPa时，相比2.5 MPa增加27.5 %；再进一步增加10 MPa，相比5 MPa增加比例为12.3 %。由此可见，接触换热系数与载荷的关系并非通常所认为的线性关系，而是随载荷的增加敏感性逐渐下降。这是因为表面接触热传递是一个十分复杂的过程。在压力作用下，当载荷增加到一定值时，由于塑性接触点的合并而产生应力释放，表面发生弹性形变的比例增加，由于微凸体之间的弹性接触面积与载荷的关系为A—p^2/3，而塑性接触面积存在关系式为A—p^[19]。因此，换热系数曲线随着载荷的增加逐渐平坦。同时，塑性变形会引起接触表面的加工硬化，使得接触表面材料的硬度增加。增加载荷而产生塑性形变的新增微凸体的数量相应减少，导致实际的接触面积也减少，因而在较大载荷下，接触换热系数对载荷的敏感性下降。此外，接触界面氧化层在载荷的作用下会产生不同程度的破裂，改变固体界面实际接触状态导致接触换热系数的变化。

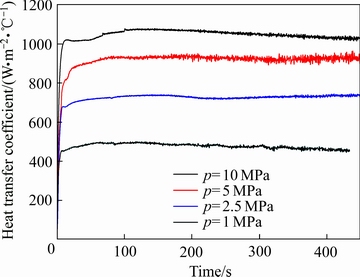
图11 载荷对接触界面换热系数的影响

Fig. 11  Effect of pressure on heat transfer coefficient of contact surface

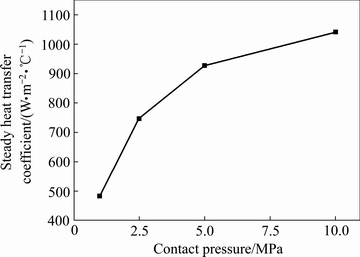
图12 不同载荷下接触界面的稳态接触换热系数

Fig. 12 Steady heat transfer coefficient of contact surface at different pressures

3.6  热流方向对接触换热系数的影响

高低温试样热流的交换导致的方向效应对接触换热系数具有重要影响。图13所示为热流方向对6061铝合金与H13钢间接触换热的影响。具体的试验条件是：接触载荷为2.5 MPa；H13试样表面粗糙度值R_a=18.38 μm；铝合金试样表面粗糙度值R_a=4.14 μm，高温和低温试样温度条件分别为200 ℃、22.5 ℃和500 ℃、22.5 ℃。由图13可知，不管是高温500 ℃还是中低温200 ℃条件，热流方向从铝合金到H13钢时的接触换热系数明显要比H13钢到铝合金的接触换热系数大，这与WILLIAMSON等^[20]的研究结果一致。造成该现象的原因可能是铝合金的比热容都要比H13钢的比热容要高，升高到同样的温度，铝合金试样所吸收的热量要高。因此，铝合金作为高温试样比H13钢作为高温试样内部所存储的热量要大。导致铝合金作为高温试样时的热量梯度要比H13作为高温试样的热量梯度大，且高低温试样温差越大，热量梯度也越大，相应接触传热系数增加的。此外，铝合金的膨胀系数大，材料硬度远小于H13钢的，相同温度下的界面实际接触面积要比H13钢作为高温试样的接触面积大，导致换热系数增大。

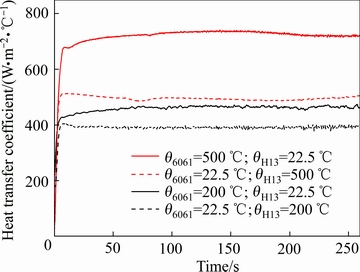
图13  热流方向对接触界面换热系数的影响

Fig. 13  Effect of heat flux direction on heat transfer coefficient of contact surface

4  结论

1) 采用FORTRAN语言建立了固体界面一维反热传导的计算程序，结合自制的测温实验装置，获得了6061铝合金与H13模具钢固体界面的接触换热系数。试样实测点的温度值与计算值误差在8 ℃以内，验证了反热传导方法的准确性。

2) 高低温试样界面接触发生后，瞬态接触换热系数在开始接触的短时间内(5 s)急剧上升，然后缓慢增大至一稳定值。

3) 当界面平均接触温度从111.5 ℃增大到211.5 ℃时，接触换热系数迅速增加。进一步提高界面平均接触温度，接触换热系数增加速率下降；表面粗糙度在1.66~2.05 μm范围内，接触换热系数下降最为显著，再增大表面粗糙度，接触换热系数下降速率降低。

4) 随着载荷的增加接触换热系数逐渐增大，但敏感性逐渐下降；热流方向从铝合金到H13钢时的接触换热系数明显要比H13钢到铝合金的接触换热系数大。

REFERENCES

[1] 刘志文, 李落星, 肖 罡, 姚再起. 热处理状态和工艺顺序对铝型材弯曲回弹的影响[J]. 湖南大学学报(自然科学版), 2014, 41(7): 23-29.

LIU Zhi-wen, LI Luo-xing, XIAO Gang, YAO Zai-qi. Influence of heat-treated condition and process sequences on the springback of aluminum bent profiles[J]. Journal of Hunan University (Natural Sciences), 2014, 41(7): 23-29.

[2] LIU Zhi-wen, LI Luo-xing, YI Jie, LI Shi-kang, WANG Zhen-hu, WANG Guan. Influence of heat treatment conditions on bending characteristics of 6063 aluminum alloy sheets[J]. Transactions of Nonferrous Metals Society of China, 2017, 27(7):1498-1506.

[3] 刘志文, 李落星. 轻量化构件弯曲短流程工艺研究现状与进展[J]. 中国有色金属学报, 2014(8): 2003-2012.

LIU Zhi-wen, LI Luo-xing. Review of bending short process for lightweight component[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(8): 2003-2012.

[4] 李落星, 刘志文, 王 冠. 一种三维变弧度挤压型材在线弯曲成形装置. 中国发明专利. CN103302125.A[P]. 2013-09-18.

LI Luo-xing, LIU Zhi-wen, WANG Guan. An on-line bending device for 3D curve extrusion profiles. CN103302125.A[P]. 2013-09-18.

[5] 朱 智, 张立文, 顾森东. Hastelloy C-276合金与硅钢间的瞬态接触换热实验研究[J]. 中南大学学报(自然科学版), 2012, 43(3): 877-882.

ZHU Zhi, ZHANG Li-wen, GU Sen-dong. Experimental investigation of transient contact heat transfer between Hastelloy C-276 and silicon steel[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 877-882.

[6] ROSOCHOWSKA M, CHONIKIEWICZ K, BALENDRA R. A new method of measuring thermal contact conductance[J]. Journal of Materials Processing Technology, 2004, 145(2): 207-214.

[7] 孙静娜, 刘楠楠, 姚 力, 罗时磊. AZ31B镁合金轧制界面接触换热系数的实验研究[J]. 热加工工艺, 2017, 46(21): 101-105.

SUN Jing-na, LIU Nan-nan, YAO Li, LUO Shi-lei. Experimental study on contact heat transfer coefficient of AZ31B magnesium alloy rolling interface[J]. Hot Working Technology, 2017, 46(21): 101-105.

[8] XU R, XU L. An experimental investigation of thermal contact conductance of stainless steel at low temperatures[J]. Cryogenics, 2005, 45(10/11): 694-704.

[9] YING L, GAO T, DAI M, YANG Y, HU P. Experimental investigation of temperature-dependent interfacial heat transfer mechanism with spray quenching for 22MnB5 steel[J]. Applied Thermal Engineering, 2017, 121: 48-66.

[10] MENDIGUREN J, ORTUBAY R, ARGANDONA E S D, Galdos L. Experimental characterization of the heat transfer coefficient under different close loop controlled pressures and die temperatures[J]. Applied Thermal Engineering, 2016, 99: 813-824.

[11] DOU R, GE T, LIU X, WEN Z. Effects of contact pressure, interface temperature, and surface roughness on thermal contact conductance between stainless steel surfaces under atmosphere condition[J]. International Journal of Heat & Mass Transfer, 2016, 94: 156-163.

[12] XIAO W, WANG B, ZHENG K, ZHOU J, LIN J. A study of interfacial heat transfer and its effect on quenching when hot stamping AA7075[J]. Archives of Civil & Mechanical Engineering, 2018, 18(3): 723-730.

[13] BAI Q, LIN J, ZHAN L, DEAN T A, BALINT D S, ZHANG Z. An efficient closed-form method for determining interfacial heat transfer coefficient in metal forming[J]. International Journal of Machine Tools & Manufacture, 2012, 56: 102-110.

[14] TARIQ A, ASIF M. Experimental investigation of thermal contact conductance for nominally flat metallic contact[J]. Heat & Mass Transfer, 2016, 52(2): 291-307.

[15] FIEBERG C, KNEER R. Determination of thermal contact resistance from transient temperature measurements[J]. International Journal of Heat & Mass Transfer, 2008, 51(5): 1017-1023.

[16] 邢 磊, 张立文, 张兴致, 岳重祥. TP2铜与3Cr2W8V模具钢的瞬态接触换热系数[J]. 中国有色金属学报, 2010, 20(4): 662-666.

XING Lei, ZHANG Li-wen, ZHANG Xing-zhi, YUE Chong-xiang. Transient contact heat transfer coefficient between TP2 copper and 3Cr2W8V die steel[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(4): 662-666.

[17] ABDULHAY B, BOUROUGA B, DESSAIN C. Thermal contact resistance estimation: influence of the pressure contact and the coating layer during a hot forming process[J]. International Journal of Material Forming, 2012, 5(3): 183-197.

[18] BECK J V, BLACKWELL B, CLAIR C. Inverse heat conduction: Ill-posed problems[M]. New York: Wiley, 1985.

[19] WHITEHOUSE D J. Handbook of surface metrology[M]. Boca Raton: CRC Press, 1994.

[20] WILLIAMSON M, MAJUMDAR A. Effect of surface deformations on contact conductance[J]. Journal of Heat Transfer, 1992, 114(4): 802-810.

Inverse estimation of contact heat transfer coefficient between 6061 aluminum alloy and H13 die steel

LIU Zhi-wen^{1, 2}, LI Luo-xing², YI Jie², WAGNG Guan²

(1. School of Mechanical Engineering, University of South China, Hengyang 421001, China;

2. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China)

Abstract: A model of inverse heat conduction for solid interfaces was established by using FORTRAN language. The transient heat transfer behavior between 6061 aluminum alloy and H13 steel was equivalently investigated by a self-made device with thermocouple. The influences of initial temperature, contact pressure, surface roughness and heat flux direction on the contact heat transfer coefficient were systematically studied. The results show that the contact heat transfer coefficient increases rapidly to a certain value in a very short time (5 s), from which a much slower increase occurs. When the average contact temperature increases from 111.5 to 211.5 ℃, the contact heat transfer coefficient increases rapidly. But with the average contact temperature further increasing, the increase rate of contact heat transfer coefficient decreases. With the increase of surface roughness, the contact heat transfer coefficient decreases gradually, the most significant effect is in the range of 1.66-2.05 μm. The contact heat transfer coefficient increases gradually with the increase of contact pressure, but the sensitivity gradually decreases. The contact heat transfer coefficient for the heat flux direction from aluminum alloy to H13 steel is obviously larger than that from H13 steel to aluminum alloy.

Key words: 6061 aluminum alloy; H13 steel; inverse heat conduction; contact heat transfer coefficient; influence factors

Foundation item: Project(U1664252) supported by the National Natural Science Foundation of China; Project (2016YFB0101704) supported by the National Key Research and Development Program of China; Project(31665004) supported by the Open Fund of State Key Laboratory of Advanced Design and Manufacture for Vehicle Body of Hunan University, China; Project(2017KJ292) supported by Science and Technology Program of Hengyang, China.

Received date: 2018-04-08; Accepted date: 2018-09-21

Corresponding author: LI Luo-xing; Tel: +86-731-88821571; E-mail: llxly2000@163.com

(编辑  李艳红)

基金项目：国家自然科学基金重点资助项目(U1664252)；国家重点研发计划项目(2016YFB0101704)；湖南大学汽车车身先进设计制造国家重点实验室开放基金资助项目(31715011)；衡阳市科技计划项且(2017KJ292)

收稿日期：2018-04-08；修订日期：2018-09-21

通信作者：李落星，教授，博士；电话：0731-88821571；E-mail：llxly2000@163.com