J. Cent. South Univ. (2018) 25: 1003-1012

DOI: https://doi.org/10.1007/s11771-018-3800-1

Analyses on uniformity of particles under HPGR finished grinding system

XU Peng-yun(许鹏云)^{1, 5}, HU Cong(胡聪)², GAN Min(甘敏)³,LI Jing(李晶)⁴, PAN Xu(潘旭)⁵, YE Hong-qi(叶红齐)¹

1. School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China;

2. Northwest Mining and Geology Group Co., Ltd for Nonferrous Metals, Xi’an 710054, China;

3. School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China;

4. Basic Teaching Department, Nanchang Institute of Science and Technology, Nanchang 330108, China;

5. Hefei Cement Research and Design Institute, Hefei 230051, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: In order to deal with the disadvantages of excessive grinding and non-uniformity in finished particle under high-pressure grinding rolls (HPGR) finished grinding system, four aspects were investigated, including evaluating indicators, effects of operating factors, effect of particle uniformity on the flotation and formation mechanism of particle uniformity. Experiment of HPGR finished grinding system, cationic reverse flotation experiment and simulation test of particle bed comminution under the condition of quasi-static were carried out. Theoretical analyses indicated that both of uniformity coefficient and average particle size should be included in the uniformity analysis of the mineral particles. The results show that the effect of circulation fan impeller speed on particle uniformity is the most evident, HPGR working pressure and roll gap are second and HPGR roller speed is the last. Average particle size has a more obvious effect on the grade of flotation concentrate while uniformity coefficient has a more obvious effect on the flotation recovery. Considering the two aspects of grade and recovery, the optimal uniformity coefficient for flotation is 1.1–1.2 and the optimal average particle size for flotation is 50–55 μm. The operating factors which promote the shielding effect and compact effect in the HPGR finished grinding system should be strengthened based on the uniformity of particles.

Key words: high-pressure grinding rolls; particle uniformity; uniformity coefficient; average particle size; flotation; shielding effect; compact effect

Cite this article as: XU Peng-yun, HU Cong, GAN Min, LI Jing, PAN Xu, YE Hong-qi. Analyses on uniformity of particles under HPGR finished grinding system [J]. Journal of Central South University, 2018, 25(5): 1003–1012. DOI: https://doi.org/10.1007/s11771-018-3800-1.

1 Introduction

Due to the working principle of particle bed comminution [1], the high-pressure roller mill (HPGR) has unparalleled advantages over traditional crushers in low energy consumption, high productivity and easy maintaining [2, 3]. Recent years, equipment problems of HPGR such as roller surface abrasion [4, 5], cylinder oil leak [6] and mathematical model [7–9] have been solved along with the development of metal materials and manufacturing processes. Therefore, HPGR is gradually recognized and accepted by the grinding industry such as cement [10, 11] and mineral processing [12, 13], and becoming one of the principal means to reduce cost and increase competitiveness for cement plant or dressing plant. However, there are some disputes on the process flow of HPGR. How to dispose the HPGR in grinding system and bring into playing the comprehensive benefits of HPGR effectively have been the focus of ongoing disputes [14–16]. Primary crushing system, combination grinding system and finished grinding system were proposed by the industry. It is generally considered the primary crushing system characterized by simple configuration process and convenient operation. The combination grinding system is advantageous to control the size and morphology of finished particle. But both of primary crushing system and combination grinding system are failed to maximize the effect of energy saving which is caused by the particle bed comminution of HPGR.

Compared with the former two systems, the finished grinding system, combined with dry separator, can not only satisfy the need of the arid mining area, but also save energy effectively. There are some famous arid mining areas noticing this grinding system such as Platinum in South Africa, Iron Ore in India and the mining district in Northwest China [14]. Unfortunately, there are also disadvantages in the finished grinding system of HPGR that should not be neglected. On one hand, the phenomenon of excessive grinding which is caused mainly by the instability of air classification exists widely in the finished grinding system. On the other hand, finished particle of HPGR finished grinding system is not uniform [17]. Previous studies have shown that fine particles caused by excessive grinding and uniformities of particles have a substantial negative impact on the concentrate grade and recovery of mineral separation [18–22]. That is to say, disadvantages of finished grinding system are fatal to mineral processing, which seriously hampered the promotion and application of this system in the mining industry. Therefore, it’s significant to study the particle uniformity of finished grinding system and its influence on flotation from the perspective of promotion and application.

In light of the above ideas, four aspects were studied in this paper to deal with the disadvantages of finished grinding system. Firstly, an evaluating indicator system was established for finished grinding system based on the RRB equation, including the evaluating indicators of uniformity coefficient and average particle size. Then, the effects of operating factors on the indicators of uniformity coefficient and average particle size were discussed. Moreover, in order to optimize the system, flotation is given consideration as a strategic object. Finally, formation mechanism of particle uniformity in the HPGR finished grinding system is discussed.

2 Materials and methods

2.1 Mineral sample

The iron ore sample is a preselected magnetic concentrate obtained from Nanshan plant of Maanshan Iron &Steel Co. Ltd (Anhui Province, China). The ore presents a TFe grade of 32.21%, with an ultimate compressive strength at 125.26 MPa. To further understand the nature of the ore sample, XRD diffraction analysis was conducted, and the result is shown in Figure 1(a). Figure 1(a) shows that the ore is composed of different kinds of minerals, the iron mineral is mainly magnetite and the gangue minerals are chlorite, quartz and so on.

In addition, pure mineral of coal and calcite were used for simulation test of particle bed comminution under the condition of quasi-static. It is important to note that ultimate compressive strength of coal is 37.73 MPa and calcite is 62.14 MPa. XRD diffraction analysis results of coal and calcite are also shown in Figures 1(b) and (c) respectively.

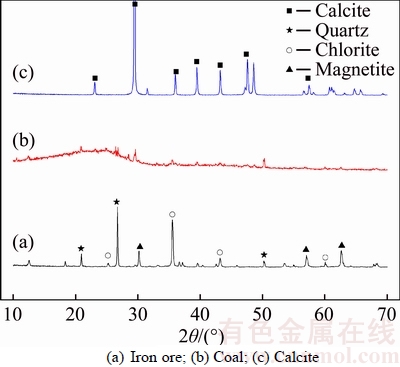
Figure 1 XRD diffraction patterns of samples

2.2 Experiment methods

2.2.1 Experiment of HPGR finished grinding system

Experiments of HPGR finished grinding system were tested in a closed-circuit experimental system, which was designed by Hefei cement research and design institute (HCRDI). The HPGR finished grinding system is mainly composed of jaw crusher, hoister, belt weigher, HPGR, V type classifier, circulation fan and finished particle warehouse, as shown in Figure 2. The experiments were conducted with 60 kg samples which were directly fed into system. Samples were first put into jaw crusher and crushed to particles under 25 mm, then, ground by HPGR. Finally, the ground samples were used for powder selecting by V-type classifier. Coarse particle was sent back to the HPGR by belt conveyor while the corresponding fine particles were gathered by cyclones and fed into the flotation test as the finished particles of HPGR finished grinding system.

2.2.2 Cationic reverse flotation experiment

Cationic reverse flotation experiments were carried out in a lab-used single flotation cell of XDF_IV0.5, which was made in prospecting machinery factory of Jilin province, China. The volume of flotation cell was 500 mL and impeller speed was 1992 r/min. 50 g finished particles of HPGR finished grinding system were mixed with 450 mL industrial water in flotation cell for 1 min. Then, calcium hydroxide was added to keep the pH at about 8.5 and the pulp was conditioned for 1 min. Moreover, starch and dodecyl-amine were added separately and the pulp was conditioned for 1 min with each reagent. It is important to note that the dosages of starch and dodecyl-amine were conducted. The dosage of starch was 12 mg/L and dodecyl-amine was 2 mg/L. The flotation time was fixed for 1 min at room temperature (22 °C). Finally, concentrates and tailings were weighed separately after filtration and drying. The grades of the two products were assessed by chemical analysis, and the recovery was calculated based on the dry weight and grade.

2.2.3 Simulation test of particle bed comminution under quasi-static condition

Simulation tests of particle bed comminution were performed on an electro-hydraulic servo closed-loop compression testing machine of YAW- 4206, which was made by MTS system (China) Co., LTD. The maximum testing pressure of machine is 2000 kN. As the adoption of electro hydraulic servo system, the testing machine has the characteristics of high control accuracy, short response and great adaptability. Simulation tests transform the dynamic and fast grinding process of HPGR into detectable and quasi-static grinding process of particle bed comminution, as shown in Figure 3.

2.3 Sample detecting

The laser particle analyzer of Cilas-1180 was used for detecting of particle size and the particle size distribution. The environmental scanning electron microscope (ESEM) of XL-30 was used to observe the morphology of treated test materials.

Figure 2 Process flowchart of HPGR finished grinding system

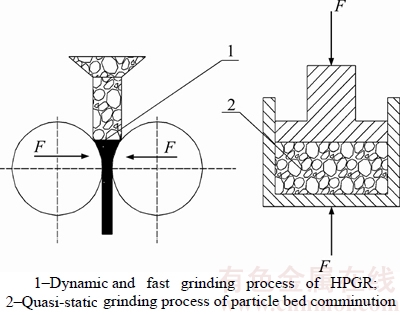
Figure 3 Simulation test principle for particle bed comminution under quasi-static condition

3 Theoretical bases of particle uniformity analyses

Essence of the particle uniformity is the range of particle size distribution [8, 9, 23]. For a certain particle group, the narrower the particle size distribution is, the more uniform it is. Normal distribution model of particle size describes the uniformity of particle as follows:

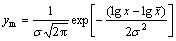               (1)

where x is particle size and is the average particle size of particle group; y_m is the mass percentage of particles whose size is smaller than x; σ is the standard deviation of particle size. Standard deviation reflects the range of particle size distribution. With the decrease of standard deviation, the range of particle size distribution becomes narrow. It means that a particle group with good uniformity has a smaller standard deviation and vice versa. Unfortunately, Normal distribution model of particle size can describe the particle uniformity, but the analyses require complex computations, especially the computations of standard deviation. For this disadvantage, normal distribution model cannot satisfy the quantitative analysis on particle uniformity.

To overcome the disadvantage of normal distribution model, uniformity coefficient is presented based on equation RRB and can be used for quantitative analysis on particle uniformity as follows [24, 25]:

                            (2)

where x₀ is characteristic particle size [26]; R is the mass percentage of particles whose size are bigger than x; n is uniformity coefficient of particle size; e is the Euler’s constant, which is the base of natural logarithms (approximately 2.7183). Logarithmic transformation is done to Eq. (2) and the result of transformation is shown as follows:

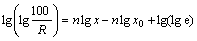            (3)

It was found that the general calculation method of uniformity coefficient is given by Eq. (3). The calculation steps are as follows: firstly, the linear fitting was applied to the data of lgx and lg[lg(100/R)], then, we get the slope of fitting line which can be considered uniformity coefficient. Accordingly, for a certain particle group, the range of particle size distribution becomes narrow with the increase of uniformity coefficient which was proposed by Eqs. (2) and (3). In other words, a particle group with good uniformity has a larger uniformity coefficient value. For example, two kinds of powder samples (named as sample A and sample B, ground by HPGR finished grinding system respectively) which have same TFe grade and different range of particle size distribution were analyzed by this method, as shown in Figure 4. Figure 4 demonstrates that the proposed model of uniformity coefficient effectively solves the problem of quantitative analysis on particle uniformity.

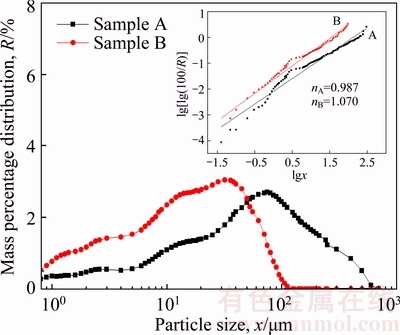
Figure 4 Particle size distributions and quantitative analysis on particle uniformity

Previous studies have confirmed that raising uniformity coefficient of mineral particles is an effective way to improve concentrate grade and recovery [18, 20, 21]. However, in the actual application, it is not enough to evaluate the mineral particles only by using uniformity coefficient. Even contradictory conclusions were obtained in condition of evaluating mineral particles only by uniformity coefficient, the same conditions of cationic reverse flotation experiments were carried out on the sample A (n_A=0.987) and sample B (n_B=1.070) as shown in Figure 4. As the uniformity coefficient of sample B is larger than sample A, the flotation results of sample B should be better than sample A according to the general thought. But the test results have shown that the recovery of sample A is much higher than sample B under the condition of similar concentrate grade.

The contradictory came out as a result of the phenomenon of excessive grinding on sample B. Even though uniformity coefficient of sample B is larger than sample A, a large number of fine particles under 10 um which cannot be recycled by flotation appear in sample B. Therefore, considering the flotation, the aspects of uniformity coefficient and average particle size should be included in the uniformity analysis of the mineral particles.

4 Results and discussion

4.1 Effects of system operating factors on particle uniformity

HPGR as grinding equipment and V type classifier as classifying equipment, which are two important components of the HPGR finished grinding system, have great influence on uniformity coefficient and average particle size of finished particle. So, operating factors, such as HPGR roller speed u, HPGR working pressure P, HPGR roll gap d and circulation fan impeller speed f, were discussed by single factor experimental method and the results are shown in Figures 5–8.

As seen in Figure 5, uniformity coefficient of the finished particle decreases while average particle size increases with the increase of HPGR roller speed. When the HPGR roller speed is above 0.4 m/s, the decrease of uniformity coefficient and the increase of average particle size become moot.

Figure 5 Effect of HPGR roller speed on uniformity of finished particles

Figure 6 Effect of HPGR working pressure on uniformity of finished particles

Figure 7 Effect of HPGR roll gap on uniformity of finished particles

As seen in Figure 6, both the uniformity coefficient and average particle size decrease with the augment of HPGR working pressure. Furthermore, the decrease of average particle size is stop at HPGR working pressure of 5.5 N/mm², but the decrease of uniformity coefficient still exists in a certain extent.

Figure 8 Effect of circulation fan impeller speed on uniformity of finished particles

As seen in Figure 7, both the uniformity coefficient and average particle size increase with the augment of HPGR roll gap. There is a significant linear relationship between average particle size and HPGR roll gap. As seen in Figure 8, with the increase of circulation fan impeller speed, uniformity coefficient decreases significantly, while the average particle size increases greatly. Specifically, the decrease of uniformity coefficient and increase of average particle size become more intense at a circulation fan impeller speed within the range of 400 to 1200 r/min.

Comparison analysis of the effects of four operating factors on uniformity coefficient and average particle size shows that the effect of circulation fan impeller speed on particle uniformity is the most evident, HPGR working pressure and roll gap are second and HPGR roller speed is the last. Considering the actual situation and working conditions of HPGR finished grinding system [9], system operating factors of circulation fan impeller speed and HPGR working pressure should be given priority to adjust.

4.2 Effect of particle uniformity on flotation

In order to explore the optimum uniformity coefficient and average particle size, cationic reverse flotation experiments were carried out. Different kinds of finished particles obtained from the HPGR finished grinding system experiments mentioned in section 4.1 were used for the cationic reverse flotation experiment. Experiment results based on the variables of uniformity coefficient and average particle size are shown in Figures 9 and 10.

As seen in Figure 9(a), high grade flotation concentrates can be obtained in the condition of higher uniformity coefficient and smaller average particle size. Concretely, uniformity coefficient in the range of 1.0–1.2 and average particle size in the range of 22–40 μm are the most effective areas for the grade of flotation concentrates as shown in Figure 9(b). The highest grade of flotation concentrate appears in the uniformity coefficient of 1.128 and the average particle size of 22.74 μm. As seen in Figure 10(a), high flotation recovery can be obtained in the condition of higher uniformity coefficient and moderate average particle size. Concretely, uniformity coefficient in the range of 1.05–1.15 and average particle size in the range of 55–60 μm are the most effective area for the flotation recovery as shown in Figure 9(b). The highest flotation recovery appears in the uniformity coefficient of 1.09 and the average particle size of 56.85 μm.

Figure 9 Effect of particle uniformity on grade of flotation concentration

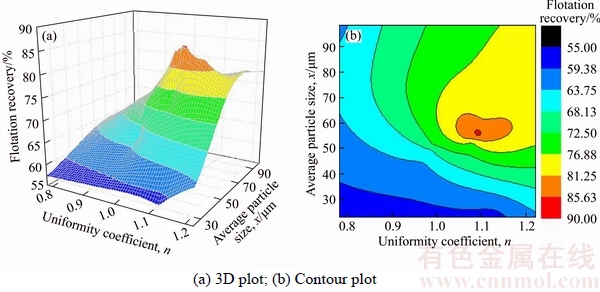
Figure 10 Effect of particle uniformity on flotation recovery

Comparative analysis was carried out on Figures 9 and 10. It is concluded that average particle size has a more obvious effect on the grade of flotation concentrate than uniformity coefficient dose. By comparison, uniformity coefficient has a more obvious effect on the flotation recovery. Considering the two aspects of grade and recovery, the optimal uniformity coefficient for flotation is 1.1–1.2 and the optimal average particle size for flotation is 50–55 μm.

5 Mechanism of particle bed comminution for particle uniformity

It is difficult to observe the grinding process of HPGR because of its dynamic and fast. So, simulation tests were performed for the mechanism of particle bed comminution occurring in HPGR. Four groups of simulation test were carried out and the schemes were designed as Table 1. Then, screenings were done to the treated test materials. Mass percentages of 20–25 mm iron ore particles were compared between the raw materials and the treated test materials. The result of each simulation tests was measured three times under the same experimental conditions, and the average value is reported as shown in Figure 11. The standard deviation, which is presented as an error bar, was calculated based on the three measurements using Origin 8.0.

Large-size particles in particle group are pressed earlier than small-size particles when test pressure is applied. This means that the large-size particles have shielding effect to small-size particles. In turn, with the increase of test pressure, the space of particle group becomes more and more small and small-size particles fill the space between large-size particles. Due to the filling of small-size particles, a dense material layer would be formed by large-size particles and small-size particles. The dense material layer can withstand greater pressure and this means that the small-size particles have compact effect to large-size particles.

Figure 11 illustrates that shielding effect and compact effect widely exist in the grinding process of HPGR. Firstly, the biggest mass percentage of 20–25 mm iron ore particles in treated test material is No. 2 test at a whopping 28.32%. This phenomenon could be attributed to shielding effect of 40–50 mm iron ore particles and compact effect of 4–5 mm iron ore particles. Secondly, mass percentage of 20–25 mm iron ore particles in No. 3 treated test material is smaller than No. 2 but bigger than No. 1. As ultimate compressive strength of coal and calcite are much lower than iron ore, a large number of small-size particles are produced when coal and calcite are pressed under test pressure. So, the phenomenon of test No. 3 could be also attributed to the compact effect of small-size particles. Finally, the smallest mass percentage of 20–25 mm iron ore particles in treated test material is No. 4 test. As the placement is layered, shielding effect of large-size particles and compact effect of small-size particles are not present in No. 4 test. This is why the mass percentage of 20–25 mm iron ore particles in No. 4 treated test material is the least.

All of the four treated test materials were observed by the environmental scanning electron microscope and more details about shielding effect and compact effect are shown in Figure12. As shown in Figure 12(a), all of the particles in the field of vision are ground under test pressure. That is to say, shielding effect of large-size particles and compact effect of small-size particles cannot be found in the No. 1 test as the test raw material in No. 1 test is a single species. It can also be seen in Figure 12(d) that all of the particles in the field of vision are ground under test pressure. So, shielding effect and compact effect also cannot be found in the No. 4 test as the different materials are layered separately. Next, turn our attention to Figures 12(b) and (c). A lot of unbroken particles can be found in Figure 12(b) and spongy structure composed of small-size particles can be found in Figure 12(c). Combining with Figure 11, it can be confirmed that shielding effect of 40–50 mm iron ore particles and compact effect of 4–5 mm iron ore particles exist in No. 2 test. Meanwhile, as ultimate compressive strength values of coal and calcite are much lower than iron ore, and a large number of small-size particles are produced when coal and calcite are pressed under test pressure. So, compact effect of small-size particles also can be confirmed to exist in No. 3 test. Therefore, scanning electron micrographs in Figure 12 prove further the existence of shielding effect and compact effect in the grinding process of HPGR.

Table 1 Scheme for simulation tests of particle bed comminution

Figure 11 Mass percentages of 20–25 mm iron ore particles in treated test material

Shielding effect and compact effect ensure the grinding occurring on the large-size particles and the excessive grinding aloof from small-size particles. Returning to the problem of particle uniformity, finished particle with uniformly distributed can be produced through this unique particle bed comminution of HPGR. Therefore, in order to improve uniformity of finished particle, the operating factors which promote the shielding effect and compact effect in the HPGR finished grinding system should be strengthened by operator.

6 Conclusions

1) Uniformity coefficient is presented based on equation RRB and can be used for quantitative analysis on particle uniformity. Unlike the uniformity analysis of other particle, both of uniformity coefficient and average particle size should be included in the uniformity analysis of the mineral particles.

2) Comparison analysis effects of the four operating factors on uniformity coefficient and average particle size show that the effect of circulation fan impeller speed is the most evident, HPGR working pressure and roll gap second and HPGR roller speed the last.

3) Average particle size has a more obvious effect on the grade of flotation concentrate; uniformity coefficient has a more obvious effect on the flotation recovery. Considering the two aspects of grade and recovery, the optimal uniformity coefficient for flotation is 1.1–1.2 and the optimal average particle size for flotation is 50–55 μm.

4) Shielding effect and compact effect ensure the grinding occurred on the large-size particles and the excessive grinding aloof from small-size particles. Particle with uniformly distributed can be produced through this unique particle bed comminution of HPGR. Therefore, in order to improve uniformity of finished particle, the operating factors which promote the shielding effect and compact effect in the HPGR finished grinding system should be strengthened by operator.

Figure 12 Scanning electron micrographs of different treated test materials

References

[1] MUTZE T. Energy dissipation in particle bed comminution [J]. International Journal of Mineral Processing, 2015, 136: 15–19. DOI: 10.1016/j.minpro.2014.10.004.

[2] KHANAL M, SCHUBERT W, TOMAS J. Discrete element method simulation of bed comminution [J]. Minerals Engineering, 2007, 20(2): 179-187. DOI: 10.1016/j.mineng. 2006.08.011.

[3] TAVARES L M. Particle weakening in high-pressure roll grinding [J]. Minerals Engineering, 2005, 18(7): 651-657. DOI: 10.1016/j.mineng.2004.10.012.

[4] SESEMANN Y, BROECKMANN C, HOFTER A. A new laboratory test for the estimation of wear in high pressure grinding rolls [J]. Wear, 2013, 302(1, 2): 1088–1097. DOI: 10.1016/j.wear.2012.10.022.

[5] GAO H, QU L G. 3D design and analysis of the crushing roller of a high-pressure grinding roller [J]. Journal of Materials Processing Technology, 2002, 129(1–3): 649–652. DOI: 10.1016/j.wear.2012.10.022.

[6] ZENG Yi-cong, XU Hai-liang, CHEN Qi, WU Bo. Research on influence of high pressure grinding rollers’ hydraulic system parameters on roll cap deviations [J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(5): 841–848. (in Chinese)

[7] DUNDAR H, BENZER H, AYDOGAN N A. Application of population balance model to HPGR crushing [J]. Minerals Engineering, 2013, 50–51: 114–120. DOI: 10.1016/j.mineng. 2013.07.005.

[8] SARAMAK D. Mathematical models of particle size distribution in simulation analysis of high-pressure grinding roll operations [J]. Physicochemical Problems of Mineral Processing, 2013, 49(1): 121–131. DOI: 10.5277/ ppmp130112.

[9] XU Peng-yun, LI Jing, LUO Heng, YE Hong-qi. Models for the particle size distribution of high-pressure grinding rolls based on fractal theory [J]. Journal of China University of Mining & Technology, 2016, 45(5): 1030–1037. (in Chinese)

[10] AYDOGAN N A, ERGUN L, BENZER H. High pressure grinding rolls (HPGR) applications in the cement industry [J]. Minerals Engineering, 2006, 19(2): 130–139. DOI: 10.1016/ j.mineng.2005.08.011.

[11] CAMALAN M, ONAL M A R. Influence of high-pressure grinding rolls on physical properties and impact breakage behavior of coarsely sized cement clinker [J]. Particulate Science and Technology, 2016, 34(3): 278–288. DOI: 10.1080/02726351.2015. 1075636.

[12] ZHU De-qing, YU Wei, ZHOU Xian-lin, PAN Jian. Strengthening pelletization of manganese ore fines containing high combined water by high pressure roll grinding and optimized temperature elevation system [J]. Journal of Central South University, 2014, 21(9): 3485–3491. DOI: 10.1007/s11771-014-2326-4.

[13] KODALI P, DHAWAN N, DEPCI T, LIN C L, MILLER J D. Particle damage and exposure analysis in HPGR crushing of selected copper ores for column leaching [J]. Minerals Engineering, 2011, 24(13): 1478–1487. DOI: 10.1016/ j.mineng.2011.07.010.

[14] JANKOVIC A, SUTHER S, WILLS T, VALERY W. Evaluation of dry grinding using HPGR in closed circuit with an air classifier [J]. Minerals Engineering, 2015, 71: 133–138. DOI: 10.1016/j.mineng.2014.10.023.

[15] YUAN Zhi-tao, LI Li-xia, HAN Yue-xin, LIU Lei, LIU Ting. Fragmentation mechanism of low-grade hematite ore in a high pressure grinding roll [J]. Journal of Central South University, 2017, 23(11): 2838–2844. DOI: 10.1007/s11771- 016-3347-y.

[16] ALTUN O, BENZER H, DUNDAR H, AYDOGAN N A. Comparison of open and closed circuit HPGR application on dry grinding circuit performance [J]. Minerals Engineering, 2011, 24: 267–275. DOI: 10.1016/j.mineng.2010.08.024.

[17] LAN Jian-wen, JIN Wei-xing, WANG Jun. Performance studies of finished mill with roller press in cement production process [J]. Journal of Xi’an University of Architecture & Technology: Natural Science Edition, 2012, 44(4): 597–604. (in Chinese)

[18] YIN Wan-zhong, WANG Ji-zhen. Effects of particle size and particle interactions on scheelite flotation [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(11): 3682-3687. DOI: 10.1016/S1003-6326(14)63515-9.

[19] RAHMAN A, AHMAD K D, MAHMOUD A. Nano- microbubble flotation of fine and ultrafine chalcopyrite particles [J]. International Journal of Mining Science and Technology, 2014, 24(4): 559–566.

[20] XIE Guang-yuan, WU Ling, OU Ze-shen, ZHANG Xiu-peng, WANG Wu-ping. Research on fine coal classified flotation flow sheet [J]. Journal of China University of Mining & Technology, 2005, 34(6): 756–760. (in Chinese)

[21] THELLA J S, MUKHERJEE A K, SRIKAKULAPU N G. Processing of high alumina iron ore slimes using classification and flotation [J]. Powder Technology, 2012, 217: 418–426. DOI: 10.1016/j.powtec.2011.10.058.

[22] YANG, Xiu-li, AI Guang-hua. Effects of surface electrical property and solution chemistry on fine wolframite flotation [J]. Separation and Purification Technology, 2016, 170: 272–279. DOI: 10.1016/j.seppur.2016.06.055.

[23] ERGULER Z A. A quantitative method of describing grain size distribution of soils and some examples for its applications [J]. Bulletin of Engineer Geology and the Environment, 2016, 75(2): 807–819. DOI: 10.1007/s10064- 015-0790-1.

[24] HOU Ying, YIN Wan-zhong, ZHU Ju-jian, YAO Jin, WANG Yu-lian, WU Kai. Relationship between parameters of size characteristic and uniformity of particle size distribution [J]. Journal of Central South University: Science and Technology, 2015, 46(9): 3183–3187. (in Chinese)

[25] G, KURAJICA S. Grinding kinetics of amorphous powder obtained by sol-gel process [J]. Powder Technology, 2010, 197(3): 165-169. DOI: 10.1016/j.powtec. 2009.09.010.

[26] LIU Shu-hua, LI Qiao-ling, XIE Guo-shuai, LI Li-hua, XIAO Heng-lin. Effect of grinding time on the particle characteristics of glass powder [J]. Powder Technology, 2016, 295(3): 133-141. DOI: 10.1016/j.powtec.2016.03.030.

(Edited by YANG Hua)

中文导读

高压辊磨终粉磨工艺制备颗粒的均匀性分析

摘要：针对高压辊磨终粉磨工艺中存在的过磨和粒度不均匀现象，本文采用高压辊磨终粉磨、阳离子反浮选以及准静态料层粉碎模拟等试验方法从评价指标、工艺条件参数的影响、颗粒均匀性对浮选的影响及颗粒均匀性强化机制等方面展开研究。理论分析表明，对颗粒均匀性分析的评价指标必须涵盖均匀性系数和平均粒径两个方面；试验结果表明，高压辊磨终粉磨工艺中选粉机循环风机转速对颗粒均匀性影响最为明显，其次是高压辊磨机工作压力和辊缝，辊面转速的影响最弱；颗粒平均粒径对方解石浮选精矿品位有较大影响而均匀性系数对精矿回收率有较大影响，综合考虑浮选精矿回收率和品位，终粉磨制备颗粒的平均粒径最佳值为50~55 μm、均匀性系数为1.1~1.2；为了提高产品颗粒均匀性，高压辊磨终粉磨工艺中有利于料层屏蔽效应和密实效应的操作参数应该得到强化。

关键词：高压辊磨；终粉磨；颗粒均匀性；均匀性系数；平均粒径；屏蔽效应；密实效应

Foundation item: Project(2013EG132088) supported by Special Program for Research Institutes of the Ministry of Science and Technology, China; Project(12010402c187) supported by Key Science and Technology Program of Anhui Province, China

Received date: 2016-10-25; Accepted date: 2017-02-23

Corresponding author: XU Peng-yun, PhD, Engineer; Tel: +86–15256046331; E-mail: xupengyun01@163.com; ORCID: 0000-0002- 1110-1566